This document discusses fast matrix factorization techniques for collaborative filtering using alternating least squares (ALS) with modifications. It proposes two new methods: 1) ALS1, which uses coordinate descent (optimizing one variable at a time) instead of least squares when computing user/item vectors in ALS. 2) IALS1, which generates synthetic items to approximate the "null user" (who consumed nothing) in implicit ALS, instead of considering each zero entry. 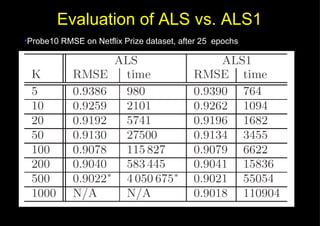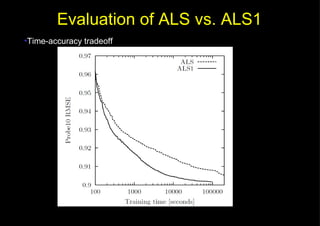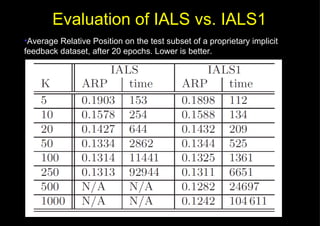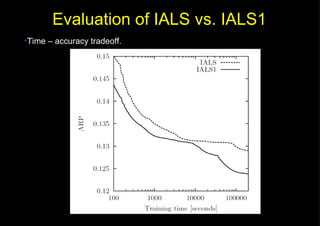Evaluation on movie recommendation datasets shows ALS1 and IALS1 offer better time-accuracy tradeoffs than ALS and IALS, especially with large feature dimensions.

1. Fast ALS-based matrix factorization for explicit and implicit feedback datasets Istv á n Pil á szy, D ávid Zibriczky, Domonkos Tikk Gravity R&D Ltd. www.gravityrd.com 28 September 20 10

2. Collaborative filtering

3. Problem setting 5 4 3 4 4 2 4 1

4. Ridge Regression

5. Optimal solution: Ridge Regression

6. Computing the optimal solution: Matrix inversion is costly: Sum of squared errors of the optimal solution: 0.055 Ridge Regression

7. RR1: RR with coordinate descent Idea: optimize only one variable of at once Start with zero: Sum of squared errors: 24.6

8. RR1: RR with coordinate descent Idea: optimize only one variable of at once Start with zero, then optimize w 1 Sum of squared errors: 7.5

9. RR1: RR with coordinate descent Idea: optimize only one variable of at once Start with zero, then optimize w 1 ,then optimize w 2 Sum of squared errors: 6.2

10. RR1: RR with coordinate descent Idea: optimize only one variable of at once Start with zero, then optimize w 1 , then w 2 , then w 3 Sum of squared errors: 5.7

11. RR1: RR with coordinate descent Idea: optimize only one variable of at once … w 4 Sum of squared errors: 5.4

12. RR1: RR with coordinate descent Idea: optimize only one variable of at once … w 5 Sum of squared errors: 5.0

13. RR1: RR with coordinate descent Idea: optimize only one variable of at once … w 1 again Sum of squared errors: 3.4

14. RR1: RR with coordinate descent Idea: optimize only one variable of at once … w 2 again Sum of squared errors: 2.9

15. RR1: RR with coordinate descent Idea: optimize only one variable of at once … w 3 again Sum of squared errors: 2.7

16. RR1: RR with coordinate descent Idea: optimize only one variable of at once … after a while: Sum of squared errors: 0.055 No remarkable difference Cost: n examples, e epoch

17. The rating matrix, R of (M x N ) is approximated as the product of two lower ranked matrices, P : user feature matrix of ( M x K ) size Q : item (movie) feature matrix of ( N x K ) size K : number of features Matrix factorization P T R T Q

18. Matrix Factorization for explicit feedb. Q P 5 5 4 3 1 R 3.3 1.3 1.3 1. 4 1. 3 1 . 9 1. 7 0.7 1.0 1.3 0.8 0 0. 7 0.4 1. 7 0. 3 2.1 2.2 6.7 1.6 1. 4 2 4 3.3 1.6 1.8

19. Finding P and Q Q P R 0.3 0.9 0.7 1.3 0.5 0 .6 1.2 0.3 1. 6 1.1 5 5 4 3 1 2 4 ? ? Init Q randomly Find p 1

20. Finding p 1 with RR Optimal solution:

21. Finding p 1 with RR Q P R 0.3 0.9 0.7 1.3 0.5 0 .6 1.2 0.3 1. 6 1.1 5 5 4 3 1 2 4 2.3 3.2

22. Initialize Q randomly Repeat Recompute P Compute p 1 with RR Compute p 2 with RR … (for each user) Recompute Q Compute q 1 with RR … (for each item) Alternating Least Squares (ALS)

23. ALS relies on RR: recomputation of vectors with RR when recomputing p 1 , the previously computed value is ignored ALS1 relies on RR1: optimize the previously computed p 1 , one scalar at once the previously computed value is not lost run RR1 only for one epoch ALS is just an approximation method. Likewise ALS1. ALS1: ALS with RR1

24. Implicit feedback Q P 1 0 R 0.5 0.1 0.2 0.7 0.3 0.1 0.1 0.7 0.3 0 0.2 0 0. 7 0.4 0.4 0. 4 1 0 0 0 0 1 1 0 0 1 0 1 1

25. The matrix is fully specified: each user watched each item. Zeros are less important, but still important. Many 0-s, few 1-s. Recall, that Idea (Hu, Koren, Volinsky): consider a user, who watched nothing compute and for this user (the null-user) when recomputing p 1 , compare her to the null-user based on the cached and , update them according to the differences In this way, only the number of 1-s affect performance, not the number of 0-s IALS: alternating least squares with this trick. Implicit feedback: IALS

26. The RR1 trick cannot be applied here  Implicit feedback: IALS1

27. The RR1 trick cannot be applied here  But, wait…! Implicit feedback: IALS1

28. X T X is just a matrix. No matter how many items we have, its dimension is the same (KxK) If we are lucky, we can find K items which generate this matrix What, if we are unlucky? We can still create synthetic items. Assume that the null user did not watch these K items X T X and X T y are the same, if synthetic items were created appropriately Implicit feedback: IALS1

29. Can we find a Z matrix such that Z is small, KxK and ? We can, by eigenvalue decomposition Implicit feedback: IALS1

30. If a user watched N items,we can run RR1 with N+K examples To recompute p u , we need steps (assume 1 epoch) Is it better in practice, than the of IALS ? Implicit feedback: IALS1

31. Evaluation of ALS vs. ALS1 Probe10 RMSE on Netflix Prize dataset, after 25 epochs

32. Evaluation of ALS vs. ALS1 Time-accuracy tradeoff

33. Evaluation of IALS vs. IALS1 Average Relative Position on the test subset of a proprietary implicit feedback dataset, after 20 epochs. Lower is better.

34. Evaluation of IALS vs. IALS1 Time – accuracy tradeoff.

35. Conclusions users items We learned two tricks: ALS1: RR1 can be used instead of RR in ALS IALS1: we can create few synthetic examples to replace the not-watching of many examples ALS and IALS are approximation algorithms, so why not change them to be even more approximative ALS1 and IALS1 offer better time-accuracy tradeoffs, esp. when K is large. They can be even 10x faster (or even 100x faster, for non-realistic K values) TODO: Precision, recall, other datasets.

36. Thank you for your attention ?