The document discusses various algorithms including dynamic programming, Warshall's and Floyd's algorithms, backtracking, branch and bound, graph coloring, the n-queen problem, Hamiltonian cycles, and the sum of subsets problem. It provides examples and explanations of these algorithms, such as using dynamic programming to solve the 0-1 knapsack problem and backtracking to solve the n-queen problem by trying different placements of queens on a chessboard.

1. DESIGN AND ANALYSIS PF
ALGORITHMS
UNIT-4
ABHIMANYU MISHRA
ASSISTANT PROF.(CSE)
JETGI
24/12/16 1Abhimanyu Mishra(CSE) JETGI

2.  Dynamic programming
 Warshal’s and floyd’s algorithm
 Resource allocation problem
 Backtracking
 Branch and bound
 Graph and colouring
 N-Queen problem
 Hamiltonian cycles
 Sum of subsets
CONTENTS
24/12/16 2Abhimanyu Mishra(CSE) JETGI

3. Dynamic programming is a technique for solving problem similar to divide
and conquer by dividing a problem into sub problems whose solutions may viewed as
the result of a sequence of decisions.
Dynamic programming is a bottom-up approach and it is used when sub
problems are not independent.
Dynamic programming solution to 0-1 knapsack problem:
0 if i=0,or w=0
c[i,w]= c[i-1,w] if wi>w
max{(c[i-1,w],vi+c[i-1,w-wi]) w>=wi
Dynamic programming
24/12/16 3Abhimanyu Mishra(CSE) JETGI

4. Cont…..
24/12/16 4Abhimanyu Mishra(CSE) JETGI
Dynamic 0-1 knapsack (v,w,n,w)
1. for w=0 to W
2. do c[0,w]=0
3. for i=1 to n
4. do c[i,0]=0
5. for w=1 to W
6. do if wi=<w
7. then if vi+c[i-1,w-wi]
8. then c[i,w]=vi+c[i-1,w-wi]
9. else c[i,w]=c[i-1,w]
10. else
11. c[i,w]=c[i-1,w]

5. 24/12/16 5Abhimanyu Mishra(CSE) JETGI
Matrix-Chain Multiplication
1. n← length[p]-1
2. for i ← 1 to n
3. do m[i,i] ←0
4. for i ←2 to n
5. l is the chain length
6. do for i ←1 to n-1+1
7. do j ←i+1-1
8. m[i,j] ←∞
9. for k ←i to j-1
10. do q ←m[i,k]+m[k+1,j]+pi-1pkpj
11. if q<m[i,j]
12. then m[i,j] ←q
13. s[i,j] ←k
14. return m and s

6. Warshal’s and floyd’s algorithm
Floyd-Warshal algorithm is an algorithm which is used to find the shortest
paths among all the pairs of nodes in a graph, which does not contain any
cycles of negative length .The main advantage is its simplicity.
1. n  rows[w]
2. d  w
3. for k=1 to n
4. do for i  1 to n
5. do for j  1 to n
6. do for di
k  min (dij,dik
(k-1)+dkj
(K-1))
7. return Do
dij= wij if k=0
min[dij
(k-1),dik
(K-1)+dkj
(K-1)]
24/12/16 6Abhimanyu Mishra(CSE) JETGI

7. 24/12/16 7Abhimanyu Mishra(CSE) JETGI
Do =
1
3
24
1 8
9 1
4 2
0 8 ∞ 1
∞ 0 1 ∞
4 ∞ 0 ∞
∞ 2 9 0
D1 =
0 8 ∞ 1
∞ 0 1 ∞
4 12 0 5
∞ 2 9 0
D2 =
0 8 9 1
∞ 0 1 ∞
4 12 0 5
∞ 2 3 0
D3 =
0 8 9 1
5 0 1 ∞
4 12 0 5
7 2 3 0
D4 =
0 3 4 1
5 0 1 ∞
4 7 0 5
7 2 3 0

8. 24/12/16 8Abhimanyu Mishra(CSE) JETGI
∏0=
N 1 N 1
N N 2 N
4 N N N
N 4 4 N
∏1=
N 1 N 1
N N 2 N
3 1 N 1
N 4 4 N
∏2=
N 1 2 1
N N 2 N
3 1 N 1
N 4 2 N
∏3=
N 1 2 1
3 N 2 3
3 1 N 1
3 4 2 N
∏4=
N 4 4 1
3 N 2 3
3 4 N 1
3 4 2 N

9. 24/12/16 9Abhimanyu Mishra(CSE) JETGI
Backtracking
Backtracking is a recursive process where we start with one possible move out of
many available moves and try to solve the problem if we are able to solve the problem with
The selected move then we will print the solution else we will backtrack and select some
Other move and try to solve it. If none if the moves work out we will claim that there is no
solution for the problem.

10. 24/12/16 10Abhimanyu Mishra(CSE) JETGI
Branch and bound
It is also called as best-first search. Branch and bound is a systematic
method for solving optimization problems. When backtracking and greedy method
fails branch and bound is applied. In this process, we used to calculate the bound at
each stage and check whether it is able to give answer or not.

11. Graph and Coloring
24/12/16 11Abhimanyu Mishra(CSE) JETGI
Coloring all the vertices of a graph with colors such that no two adjacent
vertices have the same color is called as graph coloring.

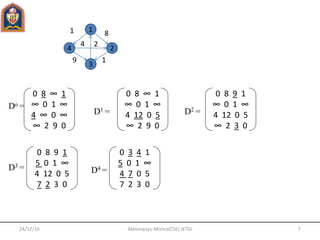
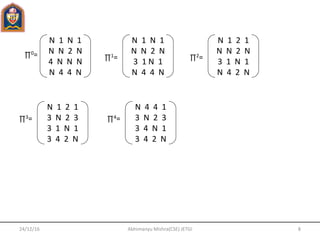
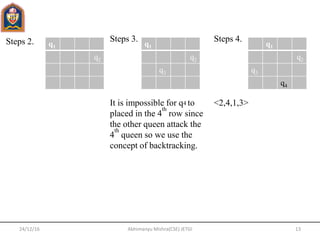
12. 24/12/16 12Abhimanyu Mishra(CSE) JETGI
In n-Queen problem, we have to place n-Queen in an n x n chessboard so that no
queen attack each other i.e., no two queen are placed on the same row, column or diagonal.
Place(k,i):
1. For j  1 to k-1
2. do if (x(j)=i) or abs(x[j]-i)=(abs(j-k))
3. Then return false
n-Queen(k,n):
1. for i  1 to n
2. do if place(k,i)
3. Then x[k]  i
4. if k=n, then print x[1…….N]
5. else n-Queen(k=1,n)
Suppose we have 4 queens i.e, q1,q2,q3,q4 Step1.
N-Queen problem
q1

13. 24/12/16 13Abhimanyu Mishra(CSE) JETGI
Steps 2. q1
q2
Steps 3.
It is impossible for q4 to
placed in the 4
th
row since
the other queen attack the
4
th
queen so we use the
concept of backtracking.
Steps 4.
<2,4,1,3>
q1
q2
q3
q1
q2
q3
q4

14. 24/12/16 14Abhimanyu Mishra(CSE) JETGI
Hamiltonian cycles
A Hamiltonian cycle is also known as Hamiltonian circuit. A
Hamiltonian cycle is a Hamiltonian Path such that there exit an edge in
graph from the last vertex to the first vertex of the Hamiltonian Path.
Whether the graph contains Hamiltonian Cycle or not. If it contains
Hamiltonian Cycle, then path is done.
For example, a Hamiltonian Cycle for the graph{0, 1, 2, 4, 3, 0}.
There are more Hamiltonian Cycles in the graph like {0, 3, 4, 2, 1, 0}
0 1 2
3 4

15. Sum of subsets
And the following graph doesn’t contain any Hamiltonian Cycle.
24/12/16 15Abhimanyu Mishra(CSE) JETGI
0 1 2
3 4

16. 24/12/16 16Abhimanyu Mishra(CSE) JETGI
Sum of subsets
In this problem, we have to find the subset of the given set S where the elements in
the set are n positive interferes in such a manner that s` belongs to S and the sum of elements
of subset s` is equal to some positive integer X. The subset problem can be calculated