The document explains the Floyd-Warshall algorithm for solving the all-pairs shortest path problem in directed graphs through dynamic programming. It outlines the algorithm's time complexity of O(v^3) and includes a recursive solution that defines the minimum path weight between vertices. Additionally, examples are provided illustrating the computation of shortest-path weights in a matrix format.

1. All Pair Shortest Path
Problem
AN EXAMPLE OF DYNAMIC PROGRAMMING
1

2. 2Floyd-Warshall algorithm for shortest
path:
 Use a different dynamic-programming formulation
to solve the all-pairs shortest-paths problem on a
directed graph G=(V,E).
 The resulting algorithm, known as the Floyd-
Warshall algorithm, runs in O (V3) time.
 negative-weight edges may be present,
 but we shall assume that there are no negative-weight cycles.

3. 3
A recursive solution to the all-pairs
shortest paths problem:
 Let dij
(k) be the weight of a shortest path from vertex i to vertex j with all
intermediate vertices in the set {1,2,…,k}. A recursive definition is given
by
 dij
(k)= wij if k=0,
 min(dij
(k-1),dik
(k-1)+dkj
(k-1)) if k 1.
 The matrix D(n)=(dij
(n)) gives the final answer-dij
(n)=
for all i,j V-because all intermediate vertices are in the set {1,2,…,n}.
),( ji

 

4. 4
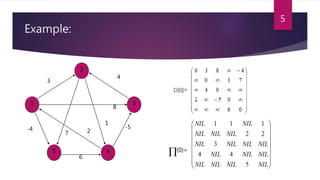
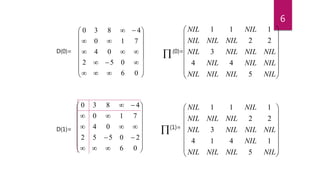
Computing the shortest-path weights
bottom up:
 FLOYD-WARSHALL(W)
 n rows[W]
 D(0) W
 for k 1 to n
 do for i 1 to n
 do for j 1 to n
 dij
(k) min(dij
(k-1),dik
(k-1)+dkj
(k-1))
 return D(n)







5. 5
Example:
1
5 4
3
2
3
4
7
-4
8
1
-5
2
6
















NILNILNILNIL
NILNILNIL
NILNILNILNIL
NILNILNIL
NILNIL
5
44
3
22
111
(0)=


6. 6





















06
052
04
710
4830
D(0)=
















NILNILNILNIL
NILNILNIL
NILNILNILNIL
NILNILNIL
NILNIL
5
44
3
22
111
(0)=
D(1)= (1)=





















06
20552
04
710
4830


















NILNILNILNIL
NIL
NILNILNILNIL
NILNILNIL
NILNIL
5
1414
3
22
111

7. 7





















06
20552
11504
710
44830
D(2)=
















NILNILNILNIL
NIL
NILNIL
NILNILNIL
NIL
5
1414
223
22
1211
(2)=
D(3)= (3)=





















06
20512
11504
710
44830


















NILNILNILNIL
NIL
NILNIL
NILNILNIL
NIL
5
1434
223
22
1211

8. 8



















06158
20512
35047
11403
44130
D(4)=
















NIL
NIL
NIL
NIL
NIL
5434
1434
1234
1244
1241
(4)=
D(5)= (5)=



















06158
20512
35047
11403
42310


















NIL
NIL
NIL
NIL
NIL
5434
1434
1234
1244
1543