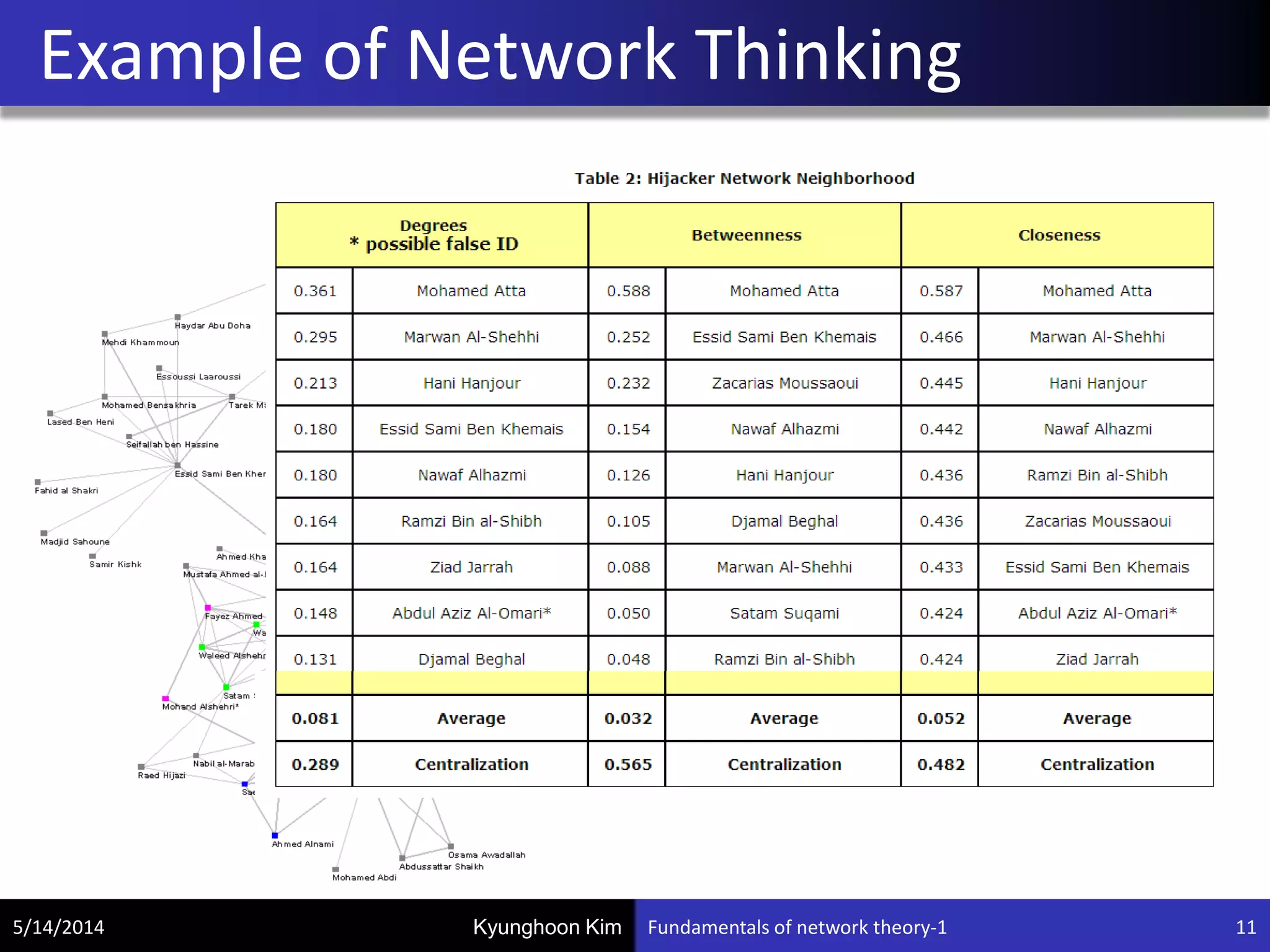
This document discusses network theory and network analysis using NetworkX. It begins with definitions of networks and graphs. Networks can be represented mathematically as graphs consisting of vertices and edges. NetworkX is introduced as a tool for representing networks as graphs and analyzing their properties. Key network measures discussed include degree, mean degree, total degree, and density. Formulas are provided for calculating these network metrics from the adjacency matrix.

1. Kyunghoon Kim
Network Analysis with networkX
Fundamentals of network theory-1
2014. 05. 14.
UNIST Mathematical Sciences
Kyunghoon Kim ( Kyunghoon@unist.ac.kr )
5/14/2014 Fundamentals of network theory-1 1

2. Kyunghoon Kim
● A NETWORK is, in its simplest form, a collection
of points joined together in pairs by lines.
What is a Network?
Newman, Mark. Networks: an introduction. OUP Oxford, 2009.
5/14/2014 Fundamentals of network theory-1 2

3. Kyunghoon Kim
● A NETWORK is, in its simplest form, a collection
of points joined together in pairs by lines.
● Network is general, but powerful means of
representing patterns of connections or
interactions between the parts of a system.
What is a Network?
Newman, Mark. Networks: an introduction. OUP Oxford, 2009.
5/14/2014 Fundamentals of network theory-1 3

4. Kyunghoon Kim
What is a Network?
Shipping (sea) networksTelecommunications networks
Air traffic networkData networks
Source: Britain From Above (http://www.bbc.co.uk/britainfromabove)
5/14/2014 Fundamentals of network theory-1 4

5. Kyunghoon Kim
● Network thinking can be applied almost
anywhere!
What is a Network?
5/14/2014 Fundamentals of network theory-1 5

6. Kyunghoon Kim
● Network thinking can be applied almost
anywhere!
Example of Network Thinking
http://journals.uic.edu/ojs/index.php/fm/article/view/941/863
My data sources were publicly released information reported in major
newspapers such as the New York Times, Wall Street Journal, Washington
Post, and the Los Angeles Times. As I monitored the investigation, it was apparent
that the investigators would not be releasing all pertinent
network/relationship information and actually may be releasing misinformation to
fool the enemy. I soon realized that the data was not going to be as complete and
accurate as I had grown accustomed to in mapping and measuring organizational
networks.
5/14/2014 Fundamentals of network theory-1 6

7. Kyunghoon Kim
Example of Network Thinking
http://www.orgnet.com/hijackers.html
5/14/2014 Fundamentals of network theory-1 7

8. Kyunghoon Kim
Example of Network Thinking
5/14/2014 Fundamentals of network theory-1 8

9. Kyunghoon Kim
Example of Network Thinking
Six (6) shortcuts were added to the
network temporarily in order to
collaborate and coordinate.
These shortcuts reduced the average
path length in the network by over 40%
thus improving the information flow in
the network - see Table 1.
When the network is brought closer
together by these shortcuts, all of the
pilots ended up in a small clique - the
perfect structure to efficiently coordinate
tasks and activities.
There is a constant dynamic
between keeping the network hidden
and actively using it to accomplish
objectives (Baker and Faulkner, 1993).
5/14/2014 Fundamentals of network theory-1 9

10. Kyunghoon Kim
Example of Network Thinking
5/14/2014 Fundamentals of network theory-1 10

11. Kyunghoon Kim
Example of Network Thinking
5/14/2014 Fundamentals of network theory-1 11

12. Kyunghoon Kim
Example of Network Thinking
Saddam Hussein
5/14/2014 Fundamentals of network theory-1 12

13. Kyunghoon Kim
Example of Network Thinking
5/14/2014 Fundamentals of network theory-1 13

14. Kyunghoon Kim
Example of Network Thinking
5/14/2014 Fundamentals of network theory-1 14

15. An Introduction to Network Theory | Kyle Findlay | SAMRA 2010 | 15
Where’s it applied?
Epidemiology (i.e. spread of diseases)
e.g. spread of foot & mouth disease in the UK in 2001 over 75 days
URL: http://www.youtube.com/watch?v=PufTeIBNRJ4

16. An Introduction to Network Theory | Kyle Findlay | SAMRA 2010 | 16
Physics
e.g. particle interactions, the structure of the universe
Where’s it applied?
URL: http://www.youtube.com/watch?v=8C_dnP2fvxk

17. An Introduction to Network Theory | Kyle Findlay | SAMRA 2010 | 17
Engineering
e.g. creation of robust infrastructure (e.g. electricity, telecoms), rust formation (natural
growth processes similar to diffusion limited aggregation)
Where’s it applied?
URL: http://www.youtube.com/watch?v=lRZ2iEHFgGo URL: http://www.youtube.com/watch?v=AEoP-XtJueo

18. An Introduction to Network Theory | Kyle Findlay | SAMRA 2010 | 18
Technology
e.g. mapping the online world, making networks resilient in the face of cyber-terrorism,
optimising cellular networks, controlling air traffic
Where’s it applied?
URL: http://www.youtube.com/watch?v=l-RoDv7c5ok URL: http://www.youtube.com/watch?v=o4g930pm8Ms
Vid not working

19. An Introduction to Network Theory | Kyle Findlay | SAMRA 2010 | 19
Where’s it applied?
Biology
e.g. fish swimming in schools, ant colonies, birds flying in formation, crickets chirping in
unison, giant honeybees shimmering
URL: http://www.youtube.com/watch?v=Sp8tLPDMUygURL: http://www.youtube.com/watch?v=YadP3w7vkJA

20. An Introduction to Network Theory | Kyle Findlay | SAMRA 2010 | 20
Medicine
e.g. cell formation, nervous system, neural networks
Where’s it applied?
Source: The Human Brain Book by Rita Carter

21. An Introduction to Network Theory | Kyle Findlay | SAMRA 2010 | 21
And, most interestingly…society
e.g. interactions between people (e.g. Facebook; group behaviour)
Where’s it applied?
URL: http://www.youtube.com/watch?v=9n9irapdON4 URL: http://www.youtube.com/watch?v=sD2yosZ9qDw

22. Kyunghoon Kim
● A network – also called a graph in the
mathematical literature – is, as we have said, a
collection of vertices joined by edges.
Networks and their Representation
Area Object Relation
Graph Theory Vertices Edges
Computer Science Nodes Links
Physics Sites Bonds
Sociology Actors Ties
5/14/2014 Fundamentals of network theory-1 22

23. Kyunghoon Kim
Networks and their Representation
Figure 6.1: Two small networks. (a) A simple graph, i.e., one having no multiedges or self-edges.
(b) A network with both multiedges and self-edges.
Newman, Mark. Networks: an introduction. OUP Oxford, 2009.
5/14/2014 Fundamentals of network theory-1 23

24. Kyunghoon Kim
Networks and their Representation
𝐴𝐴𝑖𝑖𝑖𝑖 = �
1
0
𝑖𝑖𝑖𝑖 𝑡𝑡 𝑡𝑡𝑡𝑡𝑡𝑡𝑡 𝑖𝑖𝑖𝑖 𝑎𝑎𝑎𝑎 𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒 𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏 𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣 𝑖𝑖 𝑎𝑎𝑎𝑎𝑎𝑎 𝑗𝑗,
𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜.
5/14/2014 Fundamentals of network theory-1 24

25. Kyunghoon Kim
● import networkx as nx
G = nx.Graph()
G.add_node(1)
G.add_nodes_from([1,2,3,4,5])
G.nodes()
● >>> [1, 2, 3, 4, 5]
Networks and their Representation
5/14/2014 Fundamentals of network theory-1 25

26. Kyunghoon Kim
● G.add_edge(1,2)
G.add_edges_from([(1,2),(2,4),(2,5),(3,4)])
G.edges()
● >>> [(1, 2), (2, 4), (2, 5), (3, 4)]
Networks and their Representation
5/14/2014 Fundamentals of network theory-1 26

27. Kyunghoon Kim
● nx.to_numpy_matrix(G)
● matrix([[ 0., 1., 0., 0., 0.],
[ 1., 0., 0., 1., 1.],
[ 0., 0., 0., 1., 0.],
[ 0., 1., 1., 0., 0.],
[ 0., 1., 0., 0., 0.]])
 nx.draw(G)
Networks and their Representation
5/14/2014 Fundamentals of network theory-1 27

28. Kyunghoon Kim
Networks and their Representation
5/14/2014 Fundamentals of network theory-1 28

29. Kyunghoon Kim
Networks and their Representation
= 𝐴𝐴 =
5/14/2014 Fundamentals of network theory-1 29

30. Kyunghoon Kim
Networks and their Representation
5/14/2014 Fundamentals of network theory-1 30

31. Kyunghoon Kim
Degree
5/14/2014 Fundamentals of network theory-1 31

32. Kyunghoon Kim
Degree
5/14/2014 Fundamentals of network theory-1 32

33. Kyunghoon Kim
Degree
𝑘𝑘𝑖𝑖 = �
𝑗𝑗=1
𝑛𝑛
𝐴𝐴𝑖𝑖𝑖𝑖
𝑘𝑘2 = �
𝑗𝑗=1
5
𝐴𝐴1𝑗𝑗 = 3
5/14/2014 Fundamentals of network theory-1 33

34. Kyunghoon Kim
Degree
5/14/2014 Fundamentals of network theory-1 34

35. Kyunghoon Kim
Degree
𝑘𝑘𝑖𝑖 = �
𝑗𝑗=1
𝑛𝑛
𝐴𝐴𝑖𝑖𝑖𝑖
2𝑚𝑚 = �
𝑖𝑖=1
𝑛𝑛
𝑘𝑘𝑖𝑖
5/14/2014 Fundamentals of network theory-1 35

36. Kyunghoon Kim
Total Degree m
𝑘𝑘𝑖𝑖 = �
𝑗𝑗=1
𝑛𝑛
𝐴𝐴𝑖𝑖𝑖𝑖
2𝑚𝑚 = �
𝑖𝑖=1
𝑛𝑛
𝑘𝑘𝑖𝑖
𝑚𝑚 =
1
2
�
𝑖𝑖=1
𝑛𝑛
𝑘𝑘𝑖𝑖 =
1
2
�
𝑖𝑖𝑖𝑖
𝐴𝐴𝑖𝑖𝑖𝑖
5/14/2014 Fundamentals of network theory-1 36

37. Kyunghoon Kim
Total Degree m
𝑘𝑘𝑖𝑖 = �
𝑗𝑗=1
𝑛𝑛
𝐴𝐴𝑖𝑖𝑖𝑖
2𝑚𝑚 = �
𝑖𝑖=1
𝑛𝑛
𝑘𝑘𝑖𝑖
𝑚𝑚 =
1
2
�
𝑖𝑖=1
𝑛𝑛
𝑘𝑘𝑖𝑖 =
1
2
�
𝑖𝑖𝑖𝑖
𝐴𝐴𝑖𝑖𝑖𝑖
𝑛𝑛
5/14/2014 Fundamentals of network theory-1 37

38. Kyunghoon Kim
Mean Degree c
𝑘𝑘𝑖𝑖 = �
𝑗𝑗=1
𝑛𝑛
𝐴𝐴𝑖𝑖𝑖𝑖
2𝑚𝑚 = �
𝑖𝑖=1
𝑛𝑛
𝑘𝑘𝑖𝑖
𝑐𝑐 =
1
𝑛𝑛
�
𝑖𝑖=1
𝑛𝑛
𝑘𝑘𝑖𝑖 =
2𝑚𝑚
𝑛𝑛
5/14/2014 Fundamentals of network theory-1 38

39. Kyunghoon Kim
Mean Degree c
𝑐𝑐 =
1
𝑛𝑛
�
𝑖𝑖=1
𝑛𝑛
𝑘𝑘𝑖𝑖 =
2𝑚𝑚
𝑛𝑛
>>> G.degree()
{1: 1, 2: 3, 3: 1, 4: 2, 5: 1}
>>> G.degree(2)
3
>>> Degree = G.degree().values()
[1, 3, 1, 2, 1]
>>> sum(Degree)/len(G.nodes())
1.6000000000000001
5/14/2014 Fundamentals of network theory-1 39

40. Kyunghoon Kim
Density or connectance of a graph
𝑛𝑛
2
=
1
2
𝑛𝑛(𝑛𝑛 − 1)
in a simple graph(i.e., one with no multiedges
or self-edges)
5/14/2014 Fundamentals of network theory-1 40

41. Kyunghoon Kim
Density or connectance of a graph
𝜌𝜌 =
𝑚𝑚
𝑛𝑛
2
=
2𝑚𝑚
𝑛𝑛(𝑛𝑛 − 1)
=
𝑐𝑐
𝑛𝑛 − 1
𝑛𝑛
2
=
1
2
𝑛𝑛(𝑛𝑛 − 1)
5/14/2014 Fundamentals of network theory-1 41

42. Kyunghoon Kim
Density or connectance of a graph
𝜌𝜌 =
𝑚𝑚
𝑛𝑛
2
=
2𝑚𝑚
𝑛𝑛(𝑛𝑛 − 1)
=
𝑐𝑐
𝑛𝑛 − 1
>>> total = 0.5*5*(5-1)
>>> 4/total
0.4
>>> nx.density(G)
0.4
5/14/2014 Fundamentals of network theory-1 42

43. Kyunghoon Kim
● The in-degree is the # of ingoing edges
connected to a vertex.
● The out-degree is the # of outgoing edges
connected to a vertex.
● 𝐴𝐴𝑖𝑖𝑖𝑖 = 1 if there is an edge from 𝑗𝑗 to 𝑖𝑖.
In-degree and out-degree
𝑘𝑘𝑖𝑖
𝑖𝑖 𝑖𝑖
= �
𝑗𝑗=1
𝑛𝑛
𝐴𝐴𝑖𝑖𝑖𝑖 𝑘𝑘𝑖𝑖
𝑜𝑜𝑜𝑜𝑜𝑜
= �
𝑖𝑖=1
𝑛𝑛
𝐴𝐴𝑖𝑖𝑖𝑖
5/14/2014 Fundamentals of network theory-1 43

44. Kyunghoon Kim
● A path in a network is any sequence of vertices
such that every consecutive pair of vertices in
the sequence is connected by an edge in the
network.
Paths
5/14/2014 Fundamentals of network theory-1 44

45. Kyunghoon Kim
● A path in a network is any sequence of vertices
such that every consecutive pair of vertices in
the sequence is connected by an edge in the
network.
● A path is a route across the network that runs
from vertex to vertex along the edges of the
network.
Paths
5/14/2014 Fundamentals of network theory-1 45

46. Kyunghoon Kim
● The length of a path in a network is the # of
edges traversed along the path (not the # of
vertices).
Length of Paths
5/14/2014 Fundamentals of network theory-1 46

47. Kyunghoon Kim
● The length of a path in a network is the # of
edges traversed along the path (not the # of
vertices).
● 𝐴𝐴𝑖𝑖𝑖𝑖 = 1 if there is an edge from 𝑗𝑗 to 𝑖𝑖,
and 0 otherwise.
Length of Paths
5/14/2014 Fundamentals of network theory-1 47

48. Kyunghoon Kim
● The length of a path in a network is the # of
edges traversed along the path (not the # of
vertices).
● 𝐴𝐴𝑖𝑖𝑖𝑖 = 1 if there is an edge from 𝑗𝑗 to 𝑖𝑖,
and 0 otherwise.
Length of Paths
𝑁𝑁𝑖𝑖𝑖𝑖
(2)
= �
𝑘𝑘=1
𝑛𝑛
𝐴𝐴𝑖𝑖 𝑖𝑖 𝐴𝐴𝑘𝑘𝑘𝑘 = 𝐀𝐀2
𝑖𝑖𝑖𝑖
5/14/2014 Fundamentals of network theory-1 48

49. Kyunghoon Kim
● The length of a path in a network is the # of
edges traversed along the path (not the # of
vertices).
● 𝐴𝐴𝑖𝑖𝑖𝑖 = 1 if there is an edge from 𝑗𝑗 to 𝑖𝑖,
and 0 otherwise.
i ← k , k ←j
Length of Paths
𝑁𝑁𝑖𝑖𝑖𝑖
(2)
= �
𝑘𝑘=1
𝑛𝑛
𝐴𝐴𝑖𝑖 𝑖𝑖 𝐴𝐴𝑘𝑘𝑘𝑘 = 𝐀𝐀2
𝑖𝑖𝑖𝑖
5/14/2014 Fundamentals of network theory-1 49

50. Kyunghoon Kim
● The length of a path in a network is the # of
edges traversed along the path (not the # of
vertices).
● 𝐴𝐴𝑖𝑖𝑖𝑖 = 1 if there is an edge from 𝑗𝑗 to 𝑖𝑖,
and 0 otherwise.
Length of Paths
𝑁𝑁𝑖𝑖𝑖𝑖
(2)
= �
𝑘𝑘=1
𝑛𝑛
𝐴𝐴𝑖𝑖 𝑖𝑖 𝐴𝐴𝑘𝑘𝑘𝑘 = 𝐀𝐀2
𝑖𝑖𝑖𝑖
𝑁𝑁𝑖𝑖𝑖𝑖
(3)
= �
𝑘𝑘,𝑙𝑙=1
𝐴𝐴𝑖𝑖 𝑖𝑖 𝐴𝐴𝑘𝑘𝑙𝑙 𝐴𝐴𝑙𝑙𝑗𝑗 = 𝐀𝐀3
𝑖𝑖𝑖𝑖
5/14/2014 Fundamentals of network theory-1 50

51. Kyunghoon Kim
● import numpy as np
matrix = nx.to_numpy_matrix(G)
matrix*np.transpose(matrix)
matrix([[ 1., 0., 0., 1., 1.],
[ 0., 3., 1., 0., 0.],
[ 0., 1., 1., 0., 0.],
[ 1., 0., 0., 2., 1.],
[ 1., 0., 0., 1., 1.]])
Length of Paths
𝑁𝑁𝑖𝑖𝑖𝑖
(2)
= �
𝑘𝑘=1
𝑛𝑛
𝐴𝐴𝑖𝑖 𝑖𝑖 𝐴𝐴𝑘𝑘𝑘𝑘 = 𝐀𝐀2
𝑖𝑖𝑖𝑖
5/14/2014 Fundamentals of network theory-1 51

52. Kyunghoon Kim
Loops
𝑁𝑁𝑖𝑖𝑖𝑖
(2)
=
5/14/2014 Fundamentals of network theory-1 52

53. Kyunghoon Kim
● A shortest path is a path between two vertices
such that no shorter path exists:
Shortest path (Geodesic path)
Newman, Mark. Networks: an introduction. OUP Oxford, 2009.
5/14/2014 Fundamentals of network theory-1 53

54. Kyunghoon Kim
● A shortest path is a path between two vertices
such that no shorter path exists:
● Shortest paths are necessarily self-avoiding.
● Shortest paths are not necessarily unique.
Shortest path (Geodesic path)
Newman, Mark. Networks: an introduction. OUP Oxford, 2009.
5/14/2014 Fundamentals of network theory-1 54

55. Kyunghoon Kim
● The shortest distance between vertices 𝑖𝑖 and 𝑗𝑗
is the smallest value of 𝑟𝑟 such that 𝐀𝐀𝑟𝑟
𝑖𝑖𝑖𝑖 > 0.
Shortest distance (Geodesic distance)
5/14/2014 Fundamentals of network theory-1 55

56. Kyunghoon Kim
● The shortest distance between vertices 𝑖𝑖 and 𝑗𝑗
is the smallest value of 𝑟𝑟 such that 𝐀𝐀𝑟𝑟
𝑖𝑖𝑖𝑖 > 0.
● However, in practical case we use Dijkstra’s
algorithm. We will study it later.
Shortest distance (Geodesic distance)
5/14/2014 Fundamentals of network theory-1 56

57. Kyunghoon Kim
● The diameter of a graph is the length of the
longest geodesic path between any pair of
vertices in the network for which a path
actually exists.
Diameter of a graph
5/14/2014 Fundamentals of network theory-1 57

58. Kyunghoon Kim
● Which are the most important
or central vertices in a network?
Measures and Metrics
5/14/2014 Fundamentals of network theory-1 58

59. Kyunghoon Kim
● Which are the most important
or central vertices in a network?
● Degree centrality,
Closeness centrality,
Betweenness centrality,
Eigenvector centrality,
Pagerank,
Similarity…
Measures and Metrics
5/14/2014 Fundamentals of network theory-1 59

60. Kyunghoon Kim
● Degree is sometimes called degree centrality in
the social networks literature.
● In directed networks, vertices have both an in-
degree and an out-degree, and both may be
useful as measures of centrality in the
appropriate circumstances.
Degree Centrality
5/14/2014 Fundamentals of network theory-1 60

61. Kyunghoon Kim
Degree Centrality
5/14/2014 Fundamentals of network theory-1 61

62. Kyunghoon Kim
Clustering Coefficient (local)
● For a vertex 𝑖𝑖, we define :
𝐶𝐶𝑖𝑖 =
(𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛 𝑜𝑜𝑜𝑜 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 𝑜𝑜𝑜𝑜 𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛 𝑜𝑜𝑜𝑜 𝑖𝑖 𝑡𝑡 𝑡𝑡𝑡𝑡𝑡 𝑎𝑎𝑎𝑎𝑎𝑎 𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐)
(𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛 𝑜𝑜𝑜𝑜 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 𝑜𝑜𝑜𝑜 𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛 𝑜𝑜𝑜𝑜 𝑖𝑖)
5/14/2014 Fundamentals of network theory-1 62

63. Kyunghoon Kim
Clustering Coefficient (local)
● >>> nx.clustering(G)
● {1: 0.0, 2: 0.3333, 3: 0.6666, 4: 1.0, 5: 1.0}
𝐶𝐶2 =
2
4
2
=
1
3
= 0.3333
5/14/2014 Fundamentals of network theory-1 63

64. Kyunghoon Kim
Clustering Coefficient (local)
5/14/2014 Fundamentals of network theory-1 64
“Unclustered” network “Clustered” network
None of Ego’s friends know each other* All of Ego’s friends know each other
An Introduction to Network Theory | Kyle Findlay | SAMRA 2010

65. Kyunghoon Kim
Clustering Coefficient (local)
5/14/2014 Fundamentals of network theory-1 65
– A real-world example: CEOs of Fortune 500 companies
• Which companies share directors? Clusters are colour-coded
An Introduction to Network Theory | Kyle Findlay | SAMRA 2010

66. Kyunghoon Kim
● This measures the mean distance from a vertex
to other vertices.
● Suppose 𝑑𝑑𝑖𝑖𝑖𝑖 is the length of a geodesic path
from 𝑖𝑖 to 𝑗𝑗, meaning the # of edges along the
path.
Closeness Centrality
5/14/2014 Fundamentals of network theory-1 66

67. Kyunghoon Kim
● This measures the mean distance from a vertex
to other vertices.
● Suppose 𝑑𝑑𝑖𝑖𝑖𝑖 is the length of a geodesic path
from 𝑖𝑖 to 𝑗𝑗, meaning the # of edges along the
path.
● The mean shortest distance from 𝑖𝑖 to 𝑗𝑗,
averaged over all vertices 𝑗𝑗 in the network, is
Closeness Centrality
𝑙𝑙𝑖𝑖 =
1
𝑛𝑛
�
𝑗𝑗
𝑑𝑑𝑖𝑖𝑖𝑖
5/14/2014 Fundamentals of network theory-1 67

68. Kyunghoon Kim
● Exclude for 𝑗𝑗 = 𝑖𝑖,
Closeness Centrality
𝑙𝑙𝑖𝑖 =
1
𝑛𝑛 − 1
�
𝑗𝑗(≠𝑖𝑖)
𝑑𝑑𝑖𝑖𝑖𝑖
𝑙𝑙𝑖𝑖 =
1
𝑛𝑛
�
𝑗𝑗
𝑑𝑑𝑖𝑖𝑖𝑖
5/14/2014 Fundamentals of network theory-1 68

69. Kyunghoon Kim
● This quantity takes low values for vertices that
are separated from others by only a short
shortest distance on average.
● which is the opposite of other measures.
● So commonly we take inverse :
Closeness Centrality
𝐶𝐶𝑖𝑖 =
1
𝑙𝑙𝑖𝑖
=
𝑛𝑛
∑𝑗𝑗 𝑑𝑑𝑖𝑖𝑖𝑖
5/14/2014 Fundamentals of network theory-1 69

70. Kyunghoon Kim
>>> nx.closeness_centrality(G)
{1: 0.5714, 2: 1.0, 3: 0.8, 4: 0.6666, 5: 0.6666}
Closeness Centrality
𝐶𝐶𝑖𝑖 =
1
𝑙𝑙𝑖𝑖
=
𝑛𝑛
∑𝑗𝑗 𝑑𝑑𝑖𝑖𝑖𝑖
𝐶𝐶1 =
4
∑𝑗𝑗 𝑑𝑑1𝑗𝑗
=
4
1 + 2 + 2 + 2
= 0.5714
5/14/2014 Fundamentals of network theory-1 70

71. Kyunghoon Kim
● This measures the extent to which a vertex lies
on paths between other vertices.
Betweenness Centrality
5/14/2014 Fundamentals of network theory-1 71

72. Kyunghoon Kim
● This measures the extent to which a vertex lies
on paths between other vertices.
● For example, assume that every pair of vertices
exchanges a message with equal probability
per unit time and that messages always take
the shortest path.
Betweenness Centrality
5/14/2014 Fundamentals of network theory-1 72

73. Kyunghoon Kim
● For example, assume that every pair of vertices
exchanges a message with equal probability
per unit time and that messages always take
the shortest path.
● Question : if we wait a suitably long time until
many messages have passed between each
pair of vertices, how many messages, on
average, will have passed through each vertex
en route to their destination?
Betweenness Centrality
5/14/2014 Fundamentals of network theory-1 73

74. Kyunghoon Kim
● Question : if we wait a suitably long time until
many messages have passed between each
pair of vertices, how many messages, on
average, will have passed through each vertex
en route to their destination?
● Answer : since messages are passing down
each shortest path at the same rate, the
number passing through each vertex is simply
proportional to the # of shortest paths the
vertex lies on.
Betweenness Centrality
5/14/2014 Fundamentals of network theory-1 74

75. Kyunghoon Kim
● Let 𝑛𝑛𝑠𝑠𝑠𝑠
𝑖𝑖
be 1 if vertex 𝑖𝑖 lies on the shortest path
from 𝑠𝑠 to 𝑡𝑡 and 0 if it does not or if there is no
such path.
● The betweenness centrality 𝑥𝑥𝑖𝑖 is given by
Betweenness Centrality
𝑥𝑥𝑖𝑖 = �
𝑠𝑠𝑡𝑡
𝑛𝑛𝑠𝑠𝑠𝑠
𝑖𝑖
5/14/2014 Fundamentals of network theory-1 75

76. Kyunghoon Kim
● Note that the shortest paths between a pair of
vertices need not be vertex independent,
meaning they may pass through some of the
same vertices.
● Define 𝑔𝑔𝑠𝑠𝑠𝑠 to be the total # of shortest paths
from 𝑠𝑠 to 𝑡𝑡 .
where
𝑛𝑛𝑠𝑠𝑠𝑠
𝑖𝑖
𝑔𝑔𝑠𝑠𝑠𝑠
= 0 if both 𝑛𝑛𝑠𝑠𝑠𝑠
𝑖𝑖
and 𝑔𝑔𝑠𝑠𝑠𝑠 are zero.
Betweenness Centrality
𝑥𝑥𝑖𝑖 = �
𝑠𝑠𝑡𝑡
𝑛𝑛𝑠𝑠𝑠𝑠
𝑖𝑖
𝑔𝑔𝑠𝑠𝑠𝑠
5/14/2014 Fundamentals of network theory-1 76

77. Kyunghoon Kim
>>> nx.betweenness_centrality(G)
{1: 0.0, 2: 0.5833, 3: 0.0833, 4: 0.0, 5: 0.0}
Betweenness Centrality
𝑥𝑥𝑖𝑖 = �
𝑠𝑠𝑡𝑡
𝑛𝑛𝑠𝑠𝑠𝑠
𝑖𝑖
𝑔𝑔𝑠𝑠𝑠𝑠
𝑥𝑥1 = �
𝑠𝑠𝑡𝑡
𝑛𝑛𝑠𝑠𝑠𝑠
1
𝑔𝑔𝑠𝑠𝑠𝑠
5/14/2014 Fundamentals of network theory-1 77

78. Kyunghoon Kim
>>> nx.betweenness_centrality(G)
{1: 0.0, 2: 0.5833, 3: 0.0833, 4: 0.0, 5: 0.0}
g = nx.Graph()
g.add_edges_from([(1,2),(2,3),(2,4),(2,5),(3,4),(3,5)])end = 6
for i in range(1,end):
for j in range(1,end):
#print 'from', i, 'to', j
print([p for p in nx.all_shortest_paths(g,i,j) if len(p)>2])
#print nx.dijkstra_path(g,i,j)
#print '=============='
nx.betweenness_centrality(g, normalized=False)
plt.cla()
nx.draw(g)
Betweenness Centrality
𝑥𝑥2 = �
𝑠𝑠𝑡𝑡
𝑛𝑛𝑠𝑠𝑠𝑠
2
𝑔𝑔𝑠𝑠𝑠𝑠
= 3 +
1
2
5/14/2014 Fundamentals of network theory-1 78

79. Kyunghoon Kim
>>> nx.betweenness_centrality(G)
{1: 0.0, 2: 0.5833, 3: 0.0833, 4: 0.0, 5: 0.0}
[[1, 2, 3]]
[[1, 2, 4]]
[[1, 2, 5]]
[[3, 2, 1]]
[[4, 2, 1]]
[[4, 2, 5], [4, 3, 5]]
[[5, 2, 1]]
[[5, 2, 4], [5, 3, 4]]
Betweenness Centrality
𝑥𝑥2 = �
𝑠𝑠𝑡𝑡
𝑛𝑛𝑠𝑠𝑠𝑠
2
𝑔𝑔𝑠𝑠𝑠𝑠
= 3 +
1
2
5/14/2014 Fundamentals of network theory-1 79

80. Kyunghoon Kim
>>> nx.betweenness_centrality(G)
{1: 0.0, 2: 0.5833, 3: 0.0833, 4: 0.0, 5: 0.0}
To normalize,
we use the following equation,
2
(𝑛𝑛−1)(𝑛𝑛−2)
Then,
Betweenness Centrality
𝑥𝑥2 =
2
4 × 3
�
𝑠𝑠𝑡𝑡
𝑛𝑛𝑠𝑠𝑠𝑠
2
𝑔𝑔𝑠𝑠𝑠𝑠
=
1
6
3 +
1
2
= 0.5833
5/14/2014 Fundamentals of network theory-1 80

81. Kyunghoon Kim
Appendix
● G.add_edges_from([
(1,3),(3,6),(3,7),(3,8),(6,8),(7,8),(8,9)])
5/14/2014 Fundamentals of network theory-1 81

82. Kyunghoon Kim
● nx.draw_spring(G)
● nx.to_numpy_matrix(G)
Appendix
5/14/2014 Fundamentals of network theory-1 82

83. Kyunghoon Kim
● Newman, Mark. Networks: an introduction.
OUP Oxford, 2009.
● An Introduction to Network Theory | Kyle
Findlay | SAMRA 2010
● http://journals.uic.edu/ojs/index.php/fm/articl
e/view/941/863
● http://www.orgnet.com/hijackers.html
Reference
5/14/2014 Fundamentals of network theory-1 83