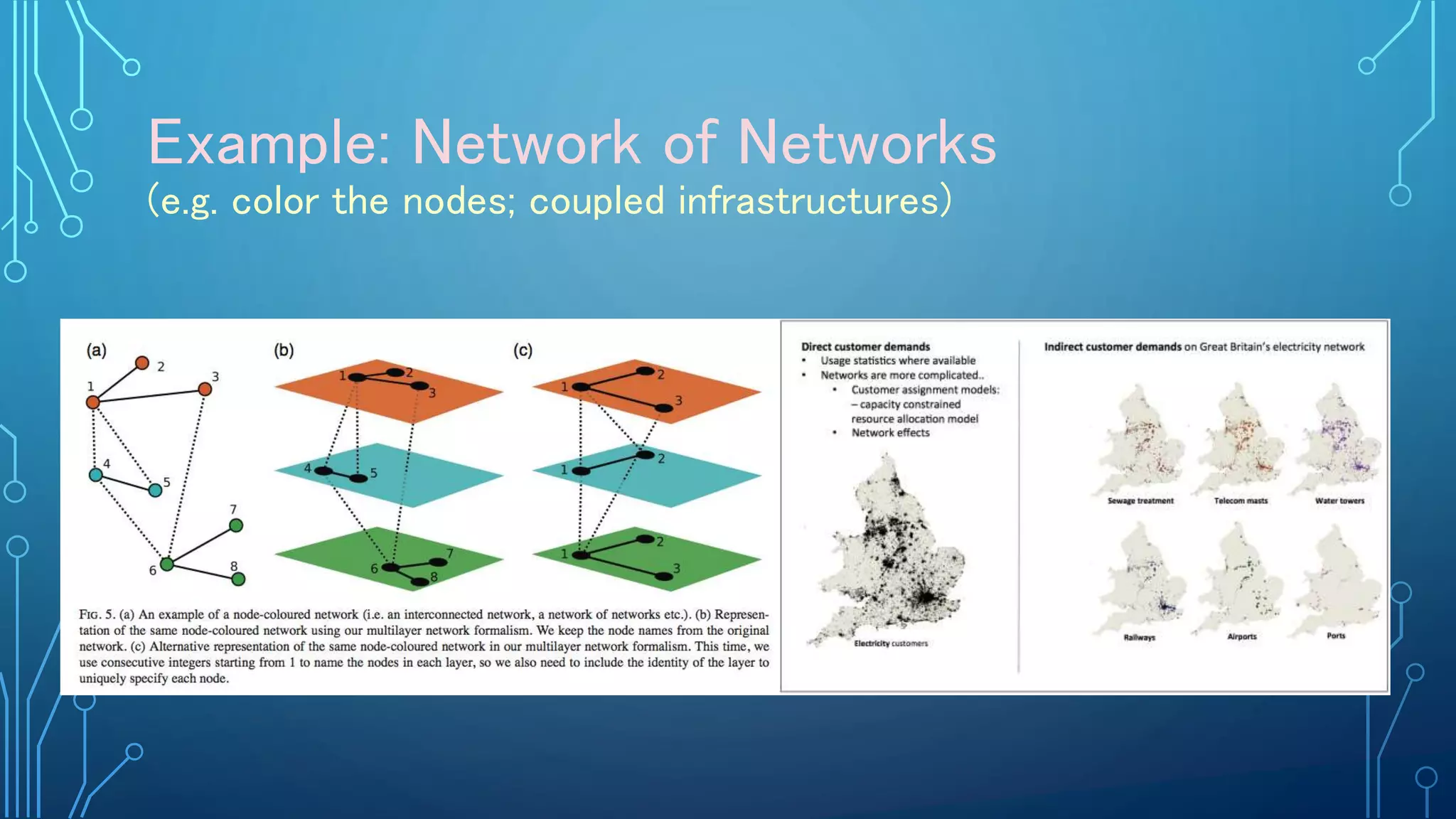
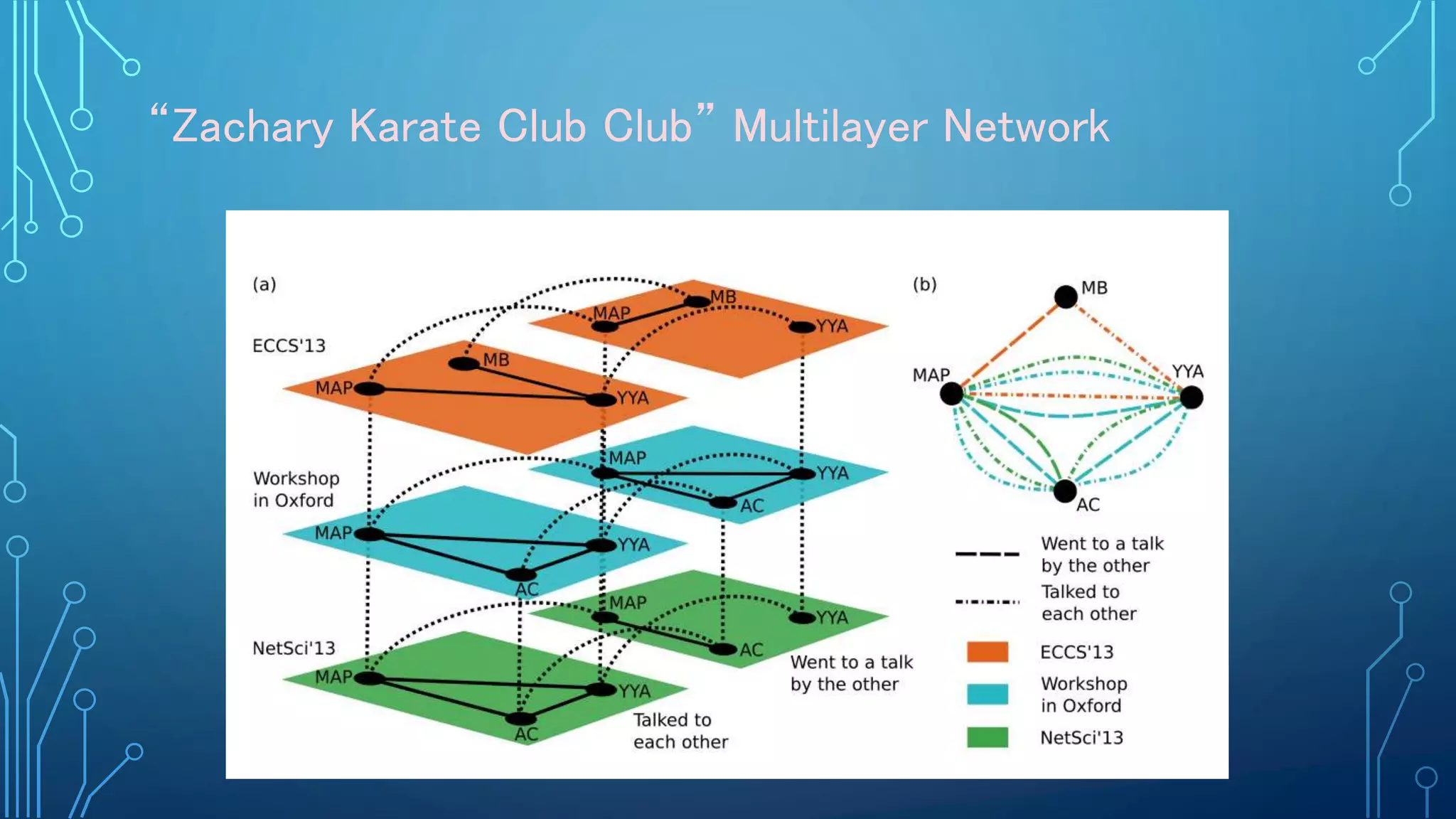
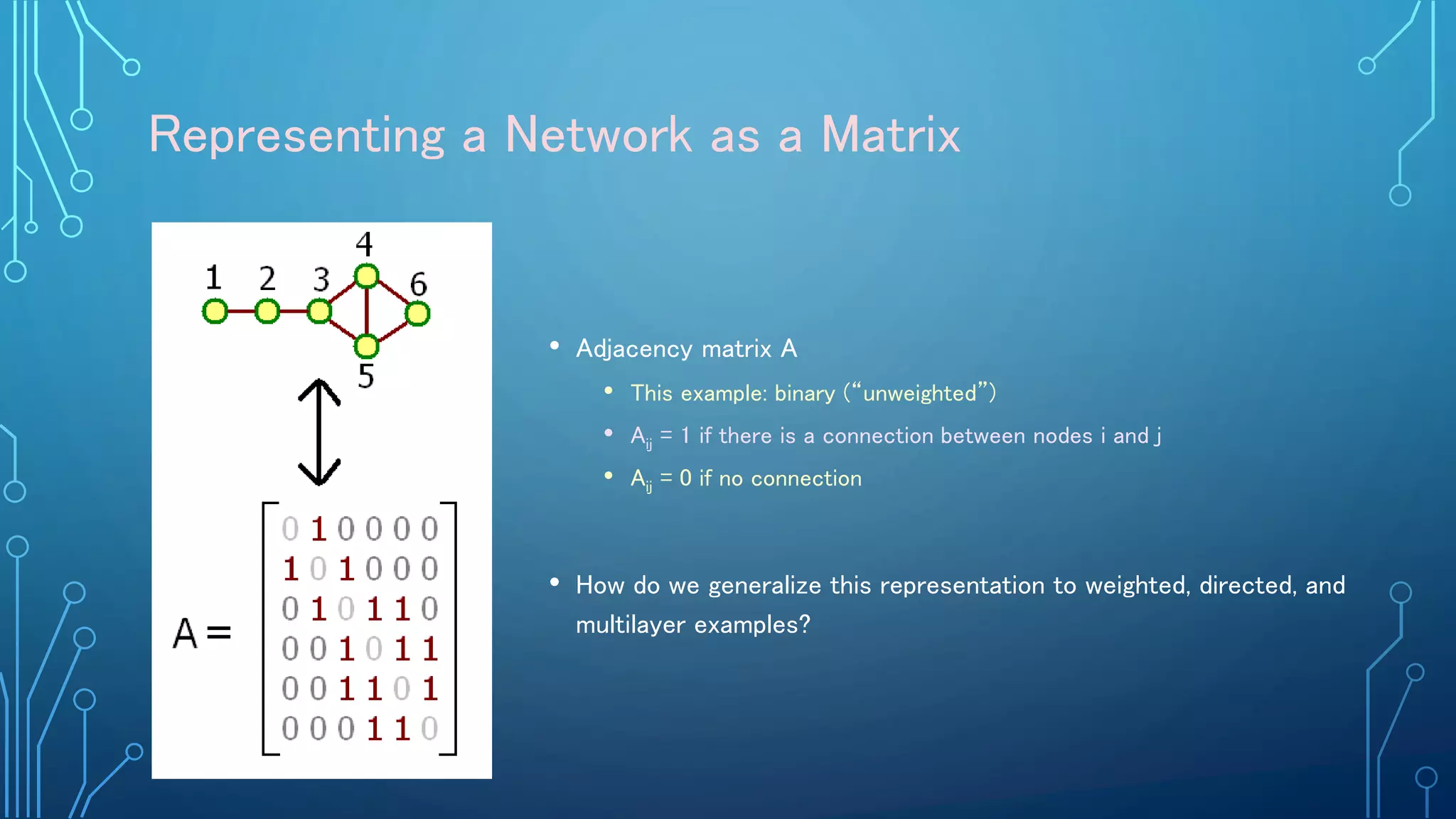
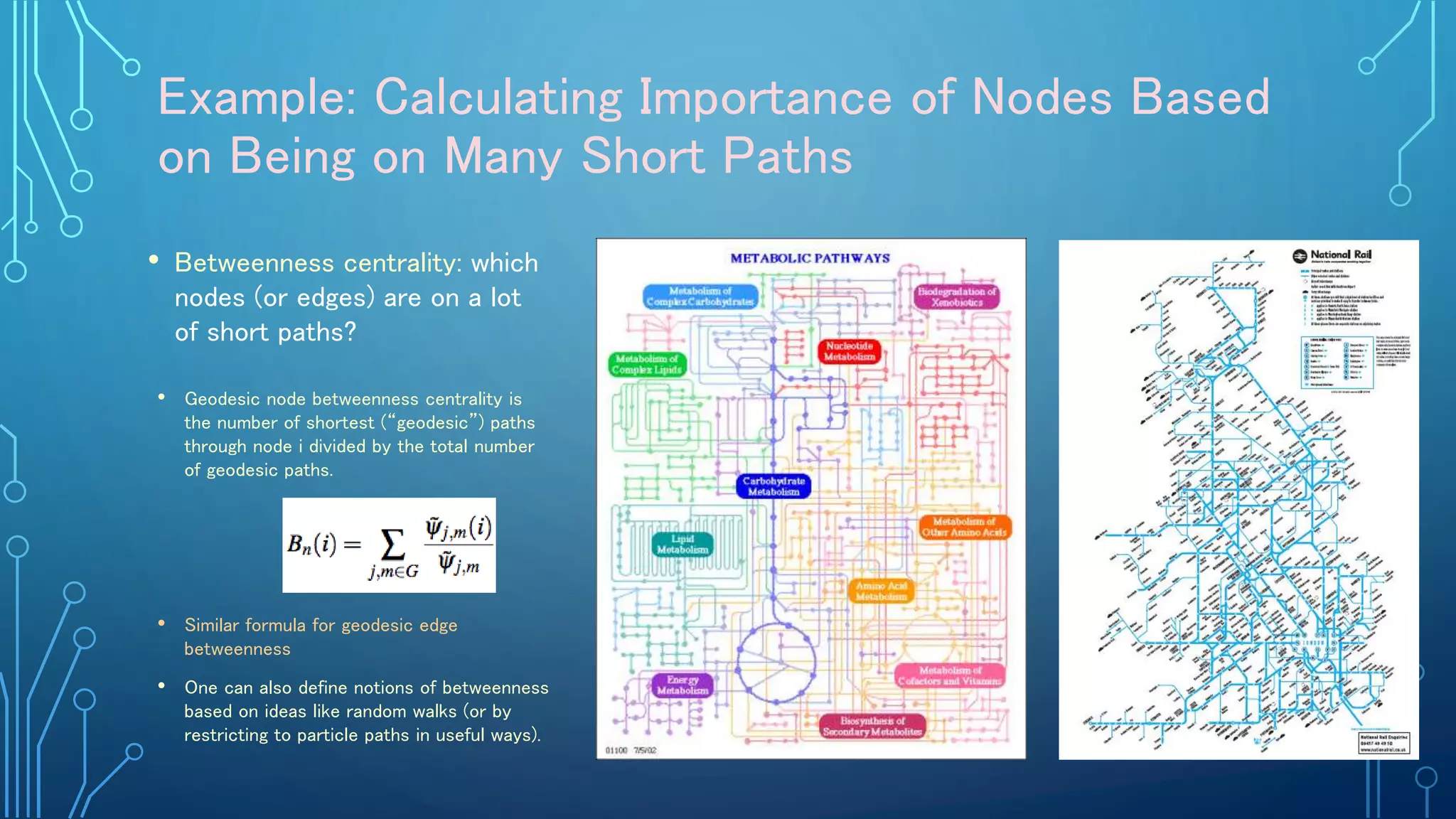
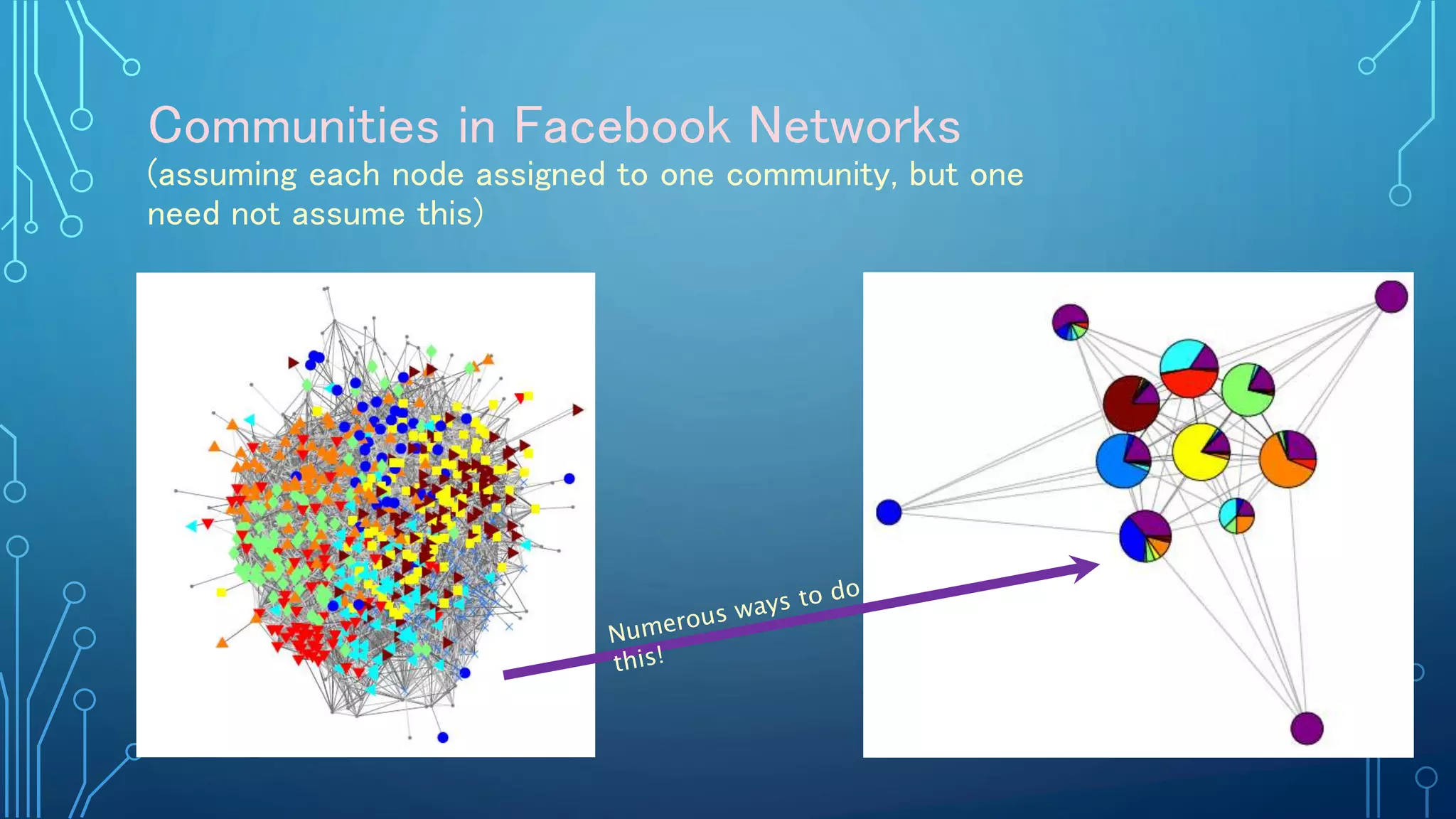
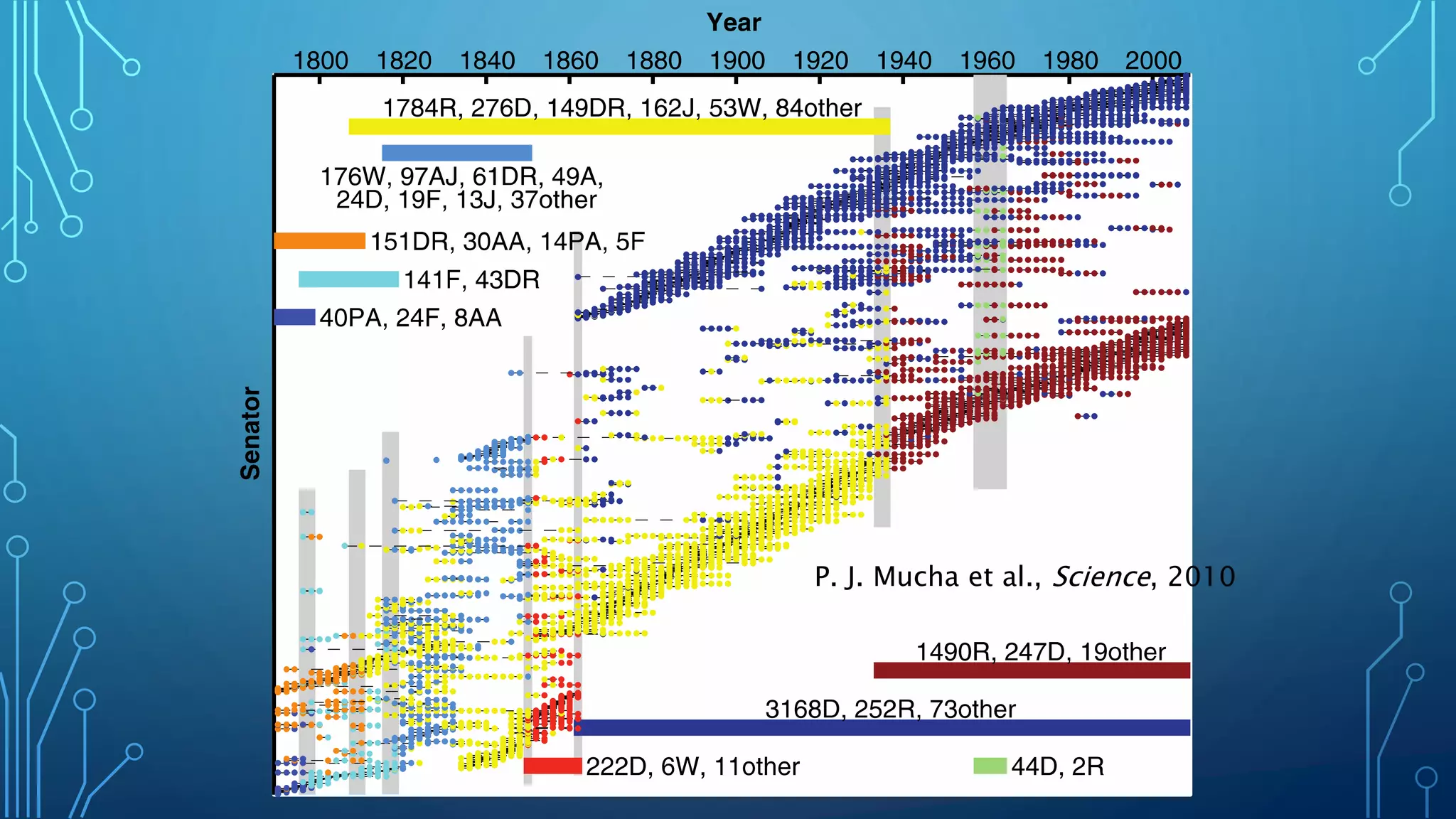
The document discusses the role of a mathematician, Mason Porter, in studying complex networks, particularly through examples like the Zachary karate club and various modeling techniques. It emphasizes the analysis of social connections, community detection, and the propagation of information or diseases within networks, alongside the mathematical methods used for these analyses. The overarching theme is the application of network theory to understand and represent various real-world phenomena through innovative analytical and computational methods.

1. Why is a Mathematician Speaking at a
Workshop about Language, Concepts,
and History?
Mason A. Porter (@masonporter)
Mathematical Institute
University of Oxford

2. What I Do
• I study networks, their structure, how networks change, dynamical
processes on networks (and how structure affects them), ways of
representing more complicated structures using networks to have more
nuanced models, and so on.
• Modeling (of networks, of dynamical processes, …)
• Analytical calculations
• Numerical calculations
• Data analysis

3. Example of a Social Network
• Example: social connections among members of a karate club

4. Some Questions That One Can Ask
• Who are the most important members of the karate club?
• How should we measure this? What are different notions of importance? How do the ways
of measuring important members and social ties change with the size of networks?
• Which are the most important social ties?
• How does information or a disease propagate in the network? Who should we
vaccinate to prevent disease spread through the whole network?
• Are there dense “communities” of friends (which may not be obvious)?
• How does the network change in time?

5. The Zachary Karate Club
(W. W. Zachary, 1977)
• This network is so (in)famous that it has its own Wikipedia entry:
https://en.wikipedia.org/wiki/Zachary%27s_karate_club
• “Network Scientists with Karate Trophies”
• http://networkkarate.tumblr.com/
• I am a member of the Zachary Karate Club Club.

6. Another Example: A Rabbit Warren
(S. H. Lee, et al., PRE, 2014)

7. “Multilayer Networks”
• Our review article: M. Kivelä et al., J. Cplx. Networks, 2014
• One motivation: But just how are those social networks among the
karate-club members defined?
• Not just one number but multi-relational: going to movies, going out to eat, etc.
• One can keep track of different “layers” of connectivity
• Keep more nuanced information and integrate different types of information
• Develop methods and tools to analyze them (very active research area)

8. Example: Multiplex Networks
(e.g. color the edges)

9. Some Current and Former Group Members

10. Example: Network of Networks
(e.g. color the nodes; coupled infrastructures)

11. “Zachary Karate Club Club” Multilayer Network

12. How I Do It
• Modeling (of networks, of dynamical processes, …)
• Analytical calculations
• Numerical calculations
• Data analysis

13. Representing a Network as a Matrix
• Adjacency matrix A
• This example: binary (“unweighted”)
• Aij = 1 if there is a connection between nodes i and j
• Aij = 0 if no connection
• How do we generalize this representation to weighted, directed, and
multilayer examples?

14. Modeling
• Example: Models of networks as different types of random graphs
• E.g., there is a uniform, independent probability p of an unweighted, undirected edge
existing between each pair of nodes
• Not realistic, but we can get much more sophisticated
• Calculate “average properties” of ensembles of random graphs
• Mathematically: A random-graph ensemble is a probability distribution on the set of graphs, and
one can calculate expectations, etc.
• Physically, an “ensemble” is an ensemble is the strict sense of statistical mechanics
• Compare these properties to sample means in numerical simulations of numerous instances of
the model
• Use appropriate random-graph models as “null models” against which to compare real
structures to examine what a given model can explain and what can depart from it

15. Modeling
• Example: equations for
dynamical process on a
network
• E.g. Watts Threshold
Model for social influence
(D. J. Watts, PNAS, 2002)
• Numerous
generalizations

16. Analytical Calculations
• One can do various calculations with exact or (more often) approximate calculations.
• One can find simpler (”lower-dimensional”) models that approximate certain features of
a dynamical process on a network.
• For example, maybe all nodes with k friends behave the same way as time becomes infinite, so now
one has an equation for every possible value of k rather than for every node (if one is asking a
question that allows one to consider the long-time limit).
• Sometimes one can rigorously prove mathematical statements about the structure
and/or dynamical processes.

17. Numerical Calculations
• One can calculate numerical properties of the ensembles of random graphs
(including very large networks, perhaps with tens of thousands or even millions of
nodes or more).
• One can directly simulate dynamical processes on networks (“equations of
motion”)
• One can calculate structural quantities of networks (either from empirical data or
random graphs)
• E.g. measures of importance (“centrality”) of nodes

18. Data Analysis
• This is closely related to many of the numerical calculations, and it also
relates to work on development and application of algorithms for network
analysis.
• Areas like statistics, machine learning, optimization, and time-series
analysis can also be involved.

19. Example: Calculating Importance of Nodes Based
on Being on Many Short Paths
• Betweenness centrality: which
nodes (or edges) are on a lot
of short paths?
• Geodesic node betweenness centrality is
the number of shortest (“geodesic”) paths
through node i divided by the total number
of geodesic paths.
• Similar formula for geodesic edge
betweenness
• One can also define notions of betweenness
based on ideas like random walks (or by
restricting to particle paths in useful ways).

20. Example: Important Mathematics Departments Using Hub
and Authority Centrality
• S. A. Meyer, P. J. Mucha, & MAP, “Mathematical genealogy and department prestige”,
Chaos, Vol. 21: 041104 (2011)
• We consider Mathematical Genealogy Project data in the US from 1973–2010 (data from
10/09)
• Example: Marty Golubitsky earned a PhD from MIT and later supervised students at
University of Houston and Ohio State.
•  Directed edge of unit weight from MIT to UH (and also from MIT to OSU)
• A university is a good authority if it hires students from good hubs, and a university is
good hub if its students are hired by good authorities.
• Caveats
• Our measurement has a time delay (only have the MITOSU edge after Marty supervises a PhD student there)
• Hubs and authorities should change in time. (We developed a method to do this in D. Taylor et al., 2015.)

22. Example: Algorithmic Detection of Dense
“Communities” of Nodes
• Survey article (very friendly!): “Communities in
Networks,” MAP, J.-P. Onnela & P. J. Mucha,
Notices of the American Mathematical Society
56, 1082–1097 & 1164–1166 (2009).
• Examples
• Gang collaborations in Los Angeles
• Facebook friendships
• Time-dependent voting communities in U.S.
Congress (e.g. obtain political realignments
directly from the data)
• Many more …

23. Communities in Facebook Networks
(assuming each node assigned to one community, but one
need not assume this)

24. How Do Different Universities Organize?
(A. L. Traud et al., Physica A, 2012)
All
people
Women
only

25. P. J. Mucha et al., Science, 2010

26. Family-tree record as a proxy of human
migration due to marriage (in Korea, across a
few hundred years)
S. H. Lee et al., Physical Review X, 2014

27. What I am Interested from Others
• Collaborations
• Interesting data sets and problems we could perhaps help give insights
into (narrow down some possibilities, which can then be explored in depth
with domain expertise)

28. What I Think I Have to Offer to Others
• Powerful tools and methods that can offer insights onto a diverse set of
problems
• Enthusiasm

29. To Tantalize: A Current Project
(note: not networks)
• Compare authors based on time-series
analysis of punctuation patterns (no
words).
• Seeking students for a Masters project or
undergraduate project.
• “Interviewing” a prospective student next
week.
• Exercise: What work/author is on the
left, and what is on the right?
• (From blog entry of Adam J. Calhoun)

30. Conclusions
• Networks provide a powerful representation of a diverse set of situations,
and they have been very successful in yielding insights into them
• We’re developing tools to do this in progressively more nuanced ways
(preserving multiple types of social ties, etc.) while retaining the power of
abstraction and large-scale computations.