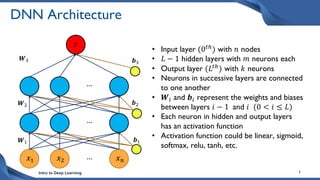
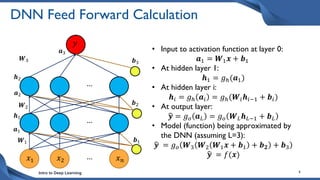
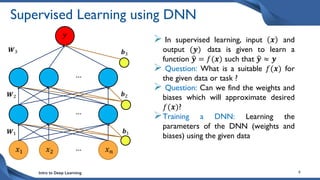
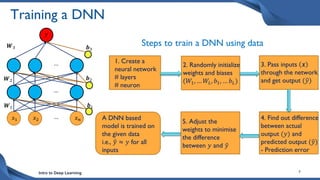
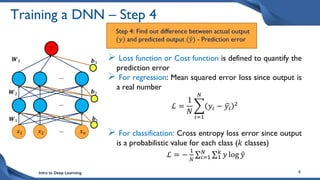
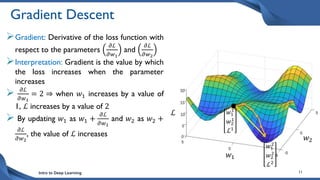
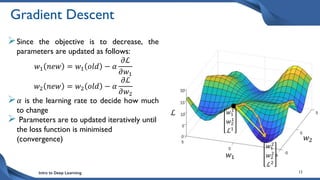
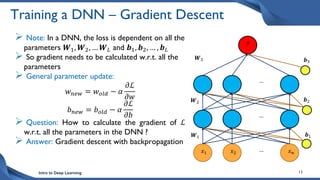
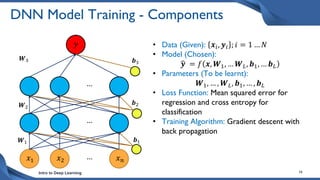
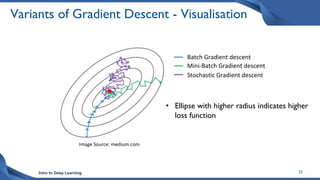
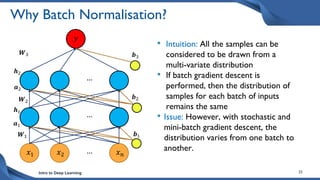
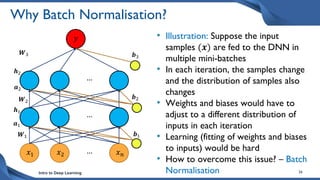
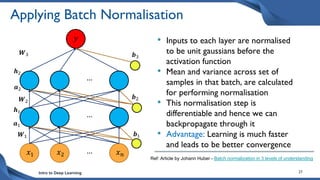
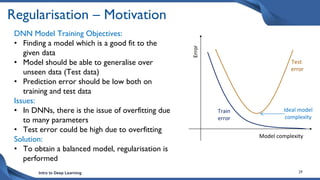
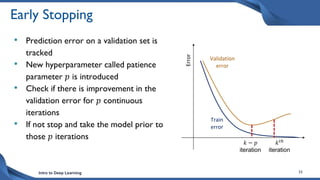
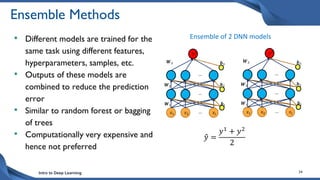
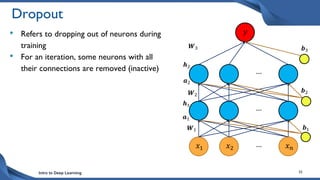
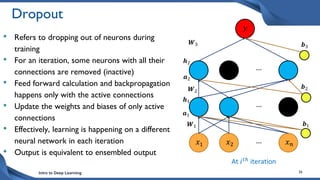
This document discusses training deep neural network (DNN) models. It explains that DNNs have an input layer, multiple hidden layers, and an output layer connected by weights and biases. Training a DNN involves initializing the weights and biases randomly, passing inputs through the network to get outputs, calculating the loss between actual and predicted outputs, and updating the weights to minimize loss using gradient descent and backpropagation. Gradient descent with backpropagation calculates the gradient of the loss with respect to each weight and bias by applying the chain rule to propagate loss backwards through the network.