The document provides an overview of topics to be covered in a social network analysis class, including techniques for analyzing social networks and common problems addressed using social network analysis. It lists several papers that will be discussed and introduces some key concepts in social network analysis, such as graphs, vertices, edges, directed/undirected networks, and partitions. It also outlines measures that can be computed for social networks at the individual, dyadic, triadic, subset and whole network levels.

1. Social Network Based Information Systems Don Steiny University of Oulu, Finland

2. Class goals Become familiar with techniques for analyzing social networks Learn some of the problems that can be solved using SNA. Learn some of the techniques used to solve problems in SNA. Give a grounding for further learning.

3. Today Get acquainted I’ll really introduce myself I will meet each of you. Overview of the papers you are getting. Overview of the major subjects in social networks we are going to cover and why they are important. Other resources. Your networks First Social Network Analysis using Pajek..

4. Papers The Strength of Weak Ties - Mark Granovetter An Experimental Study of the Small Worlds Problem - Jeffrey Travers; Stanley Milgram Scale Free Networks - Albert-László Barabási and Eric Bonabeau Social Networks and Loss of Capital - Wayne E. Baker, Robert R. Faulkner

5. More Papers The Diffusion of an Innovation among Physicians - James Colman, Elihu Katz, Herbert Menzel Collaboration Networks, Structural Holes and Innovation: A Longitudinal Study - Gautam Ahuja Social Process and Hierarchy Formation - Ivan Chase The Impact of Social Structure on Economic Outcomes - Mark Granovetter

6. Still more papers The Iron Cage Revisited: Institutional Isomorphism and Collective Rationality in Organizational Fields - Paul J. DiMaggio, Walter W. Powell Social Networks,the Tertius Iungens Orientation, and Involvement in Innovation - David Obstfeld The Social Origin of Good Ideas - Ron Burt The Sources and Consequences of Embeddedness for Economic Performance of Organizations: The Network Effect - Brian Uzzi

7. More papers yet From Community of Innovation to Community of Inertia - The Rise and Fall of the U.S. Tire Industry - Donald N. Sull *Being No One - The Self-Model of Subjectivity - Thomas Metzinger Embeddedness in the Making of Financial Capital: How Social Relations and Networks Benefit Firms Seeking Financing - Brian Uzzi

8. Whew, last of papers *What Creates Energy in Organizations - Rob Cross and Andrew Parker World Society and the Nation State - John W. Meyer; John Boli; George M. Thomas, Francisco. O Ramirez * - PAPERS WITH ASTRICK (*) are not eligible for course paper.

9. Who Does What? Anthropologists – kinship relations, friendship gift giving Social psychologists – affections Political Scientists – power relations Economists – trade and organizational relations Sociologists – Social choices

10. Some terms A graph is a set of vertices and a set of lines between pairs of vertices. A vertex (singular of vertices) is the smallest unit in a network. A line is a relation between two vertices in a network.. A line is defined by its two endpoints, which are the two vertices that are incident with the line. A loop is a special kind of line, namely a line which connects a vertex to itself. An arc is an ordered pair of vertices in which the first vertex is the sender (the tail of the arc) and the second the receiver of the relation (the head of the arc). An edge , which has no direction, is represented by an unordered pair. It does not matter which vertex is first or second in the pair. A directed graph or digraph contains one or more arcs. An undirected graph does not contain arcs: all of its lines are edges. A simple undirected graph contains neither multiple edges nor loops. A simple directed graph does not contain multiple arcs. A network consists of a graph and additional information on the vertices or the lines of the graph.

11. Our personal networks 4 work sheets Draw the network Discussion

12. Dining Table Partners

13. Pajek data files .net – network files .clu – partition files .vec – vector files .paj – project files

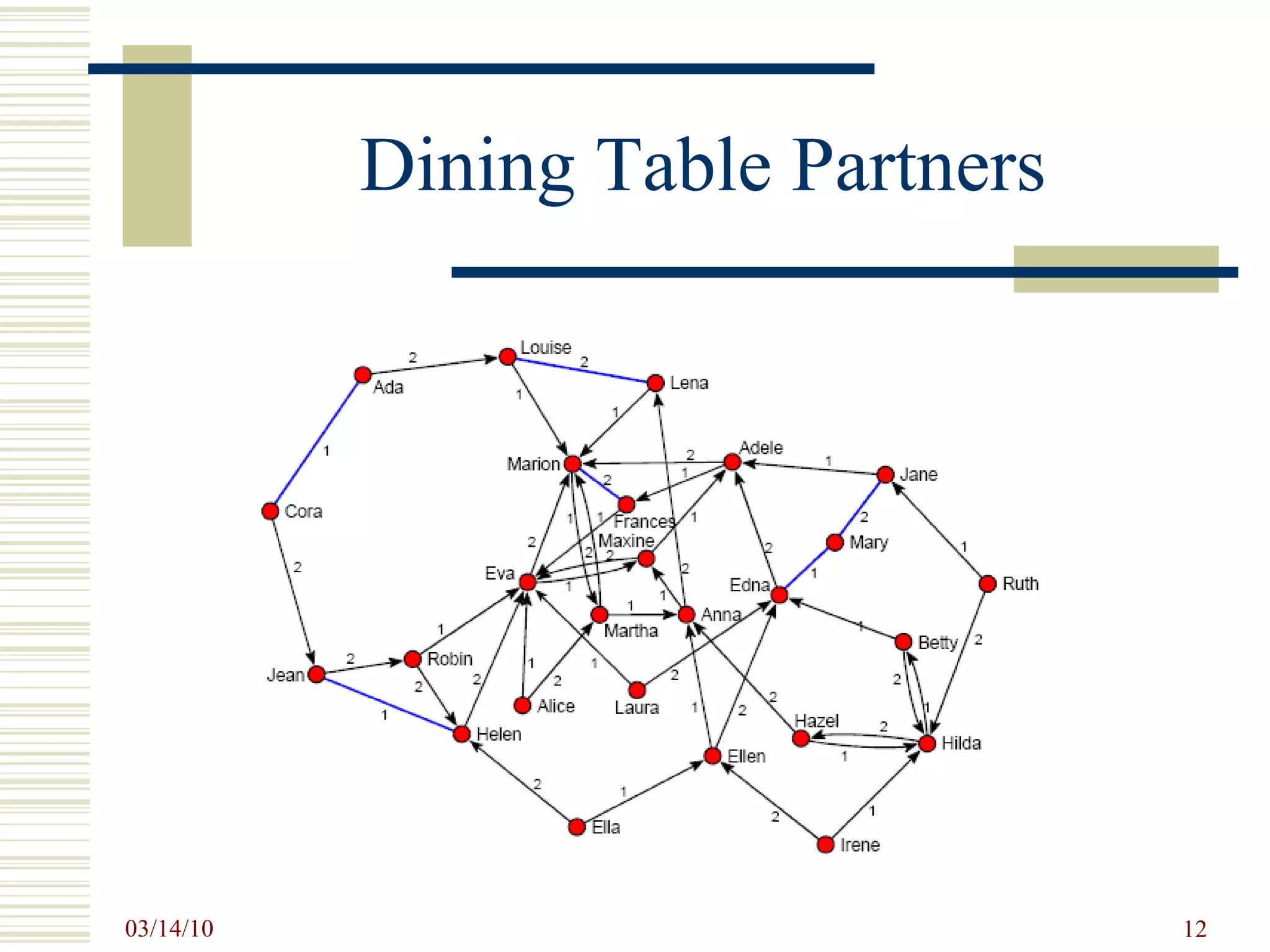
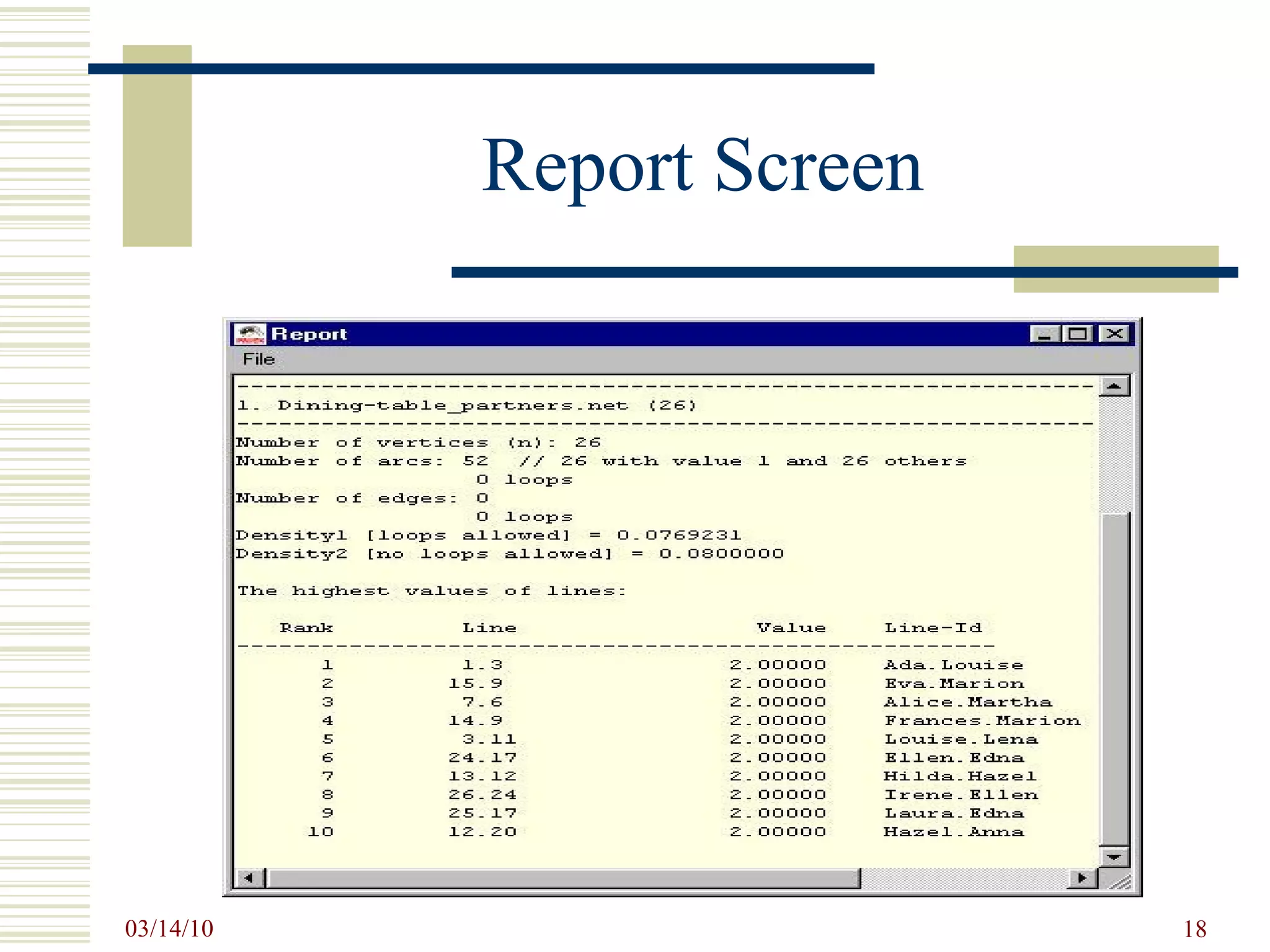
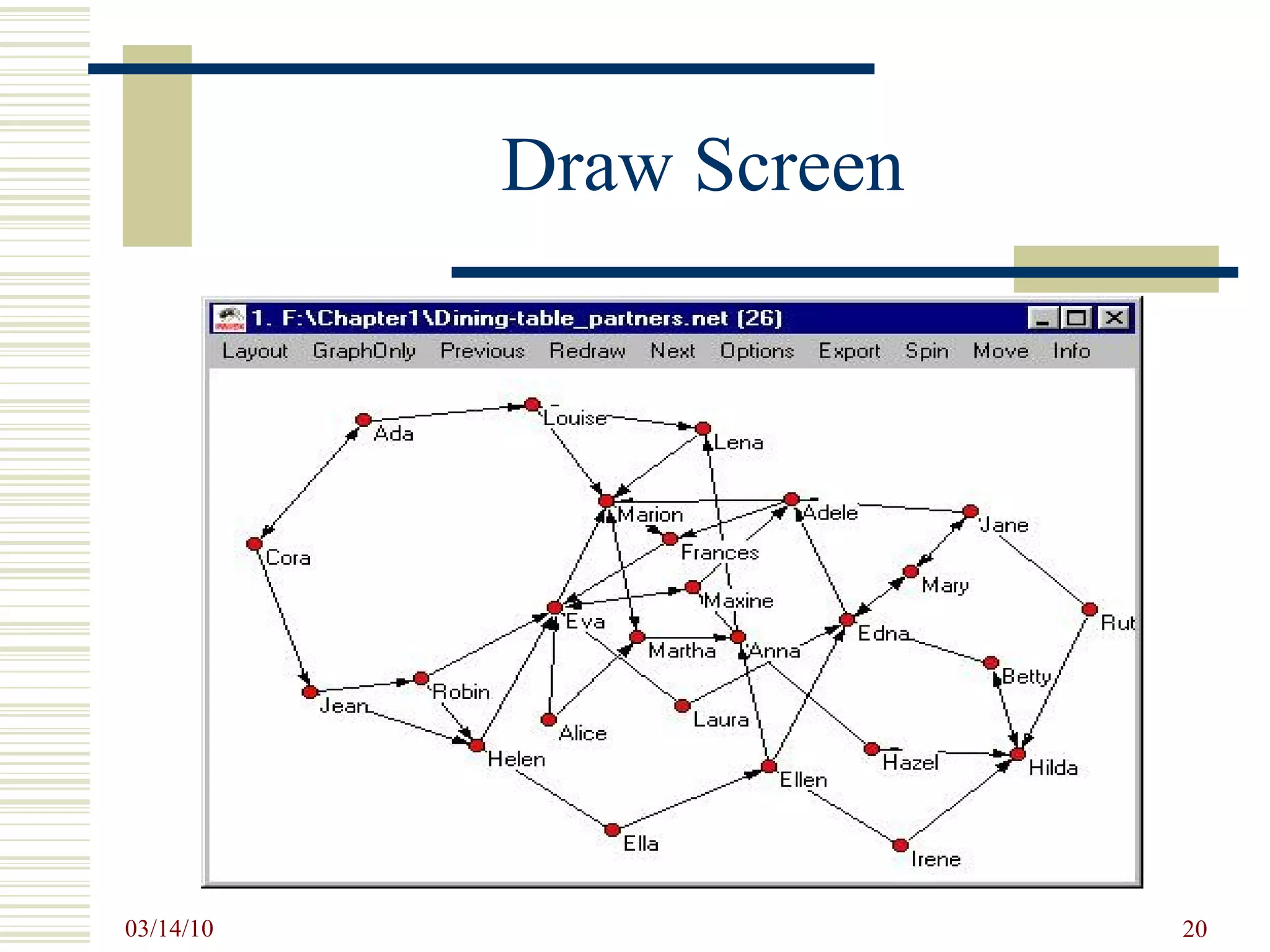
14. Pajek Data File *Vertices 26 1 "Ada" 0.1646 0.1077 0.5000 2 "Cora" 0.0481 0.3446 0.5000 3 "Louise" 0.3472 0.0759 0.5000 4 "Jean" 0.1063 0.6284 0.5000 […] 25 "Laura" 0.5101 0.6557 0.5000 26 "Irene" 0.7478 0.9241 0.5000 *Arcs 1 3 2 1 2 1 2 1 1 2 4 2 3 9 1 3 11 2 […] 25 15 1 25 17 2 26 13 1 26 24 2 *Edges

15. Pajek files Let’s find the file Dining-table_partners.net, take a look at it with notepad.

16. Pajek Main Screen

17. Convert arcs to edges

18. Report Screen

19. Dialogue Box Info->Network->General

20. Draw Screen

21. Draw Screen Experience Load the file “dining_table_partners.net” and go through the handout labeled “Draw Screen” and do the commands there. Dichotomize the network and draw it. Remove all second choices and draw the network. Use the factor option of Fruchterman Reingold to make a clearer distinction between the center and the periphery.

22. Networks as matrices – joke network

23. Matrix of joke network

24. Thinking about matrices How would the matrix be different if it was an undirected graph? How would you represent values for the lines?

25. Create Pajek file from joke network Translates graphs into a simple file format Usually this is automated Use Pajek to create the network – hard work. How could Excel, Access, SQL or other programs be used to generate networks?

26. Compare networks Generate random networks with the same number of nodes as the dining table partners network. Use Draw->Info->All Properties to compare crossing lines. What is the systematic difference?

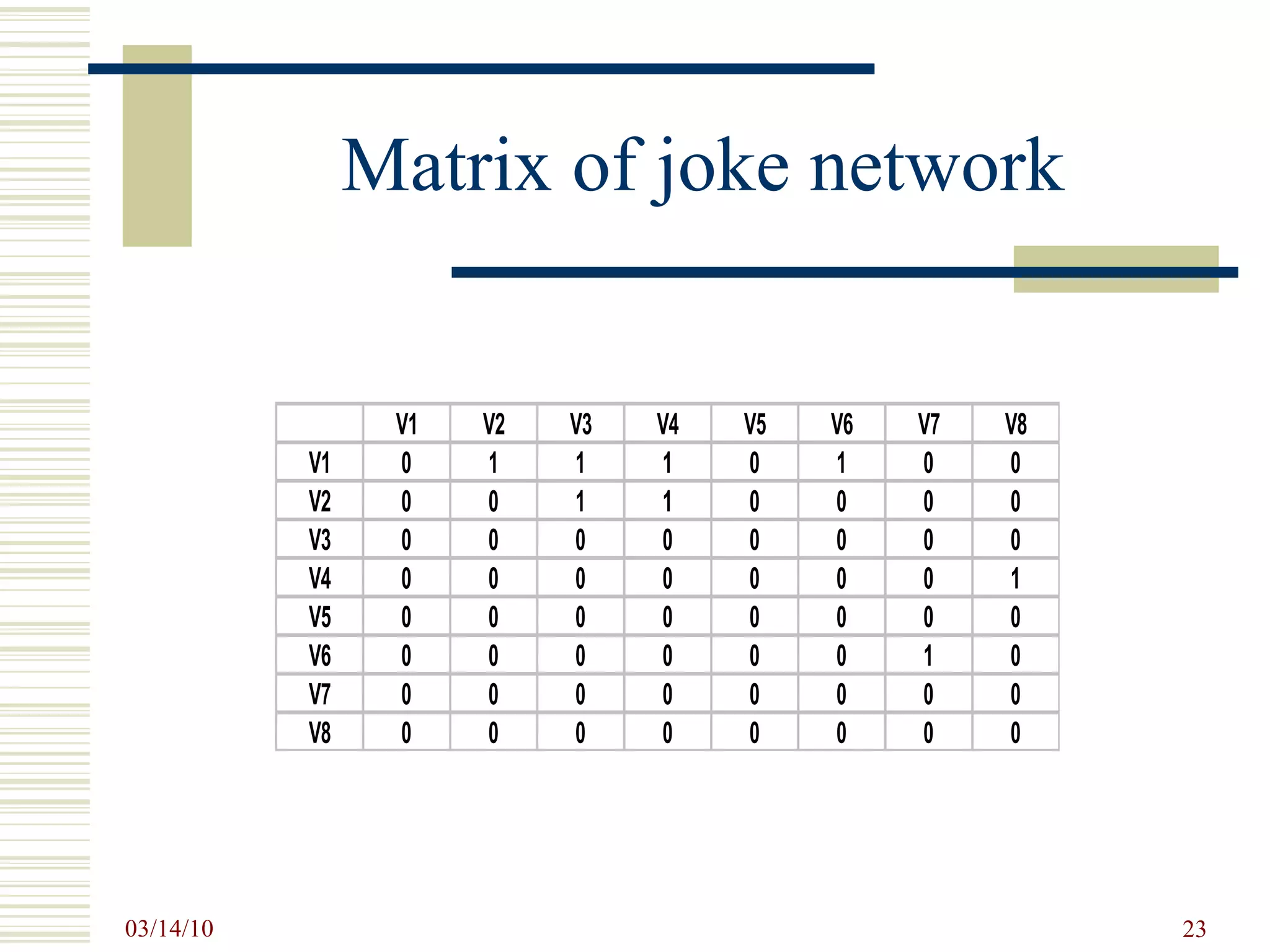
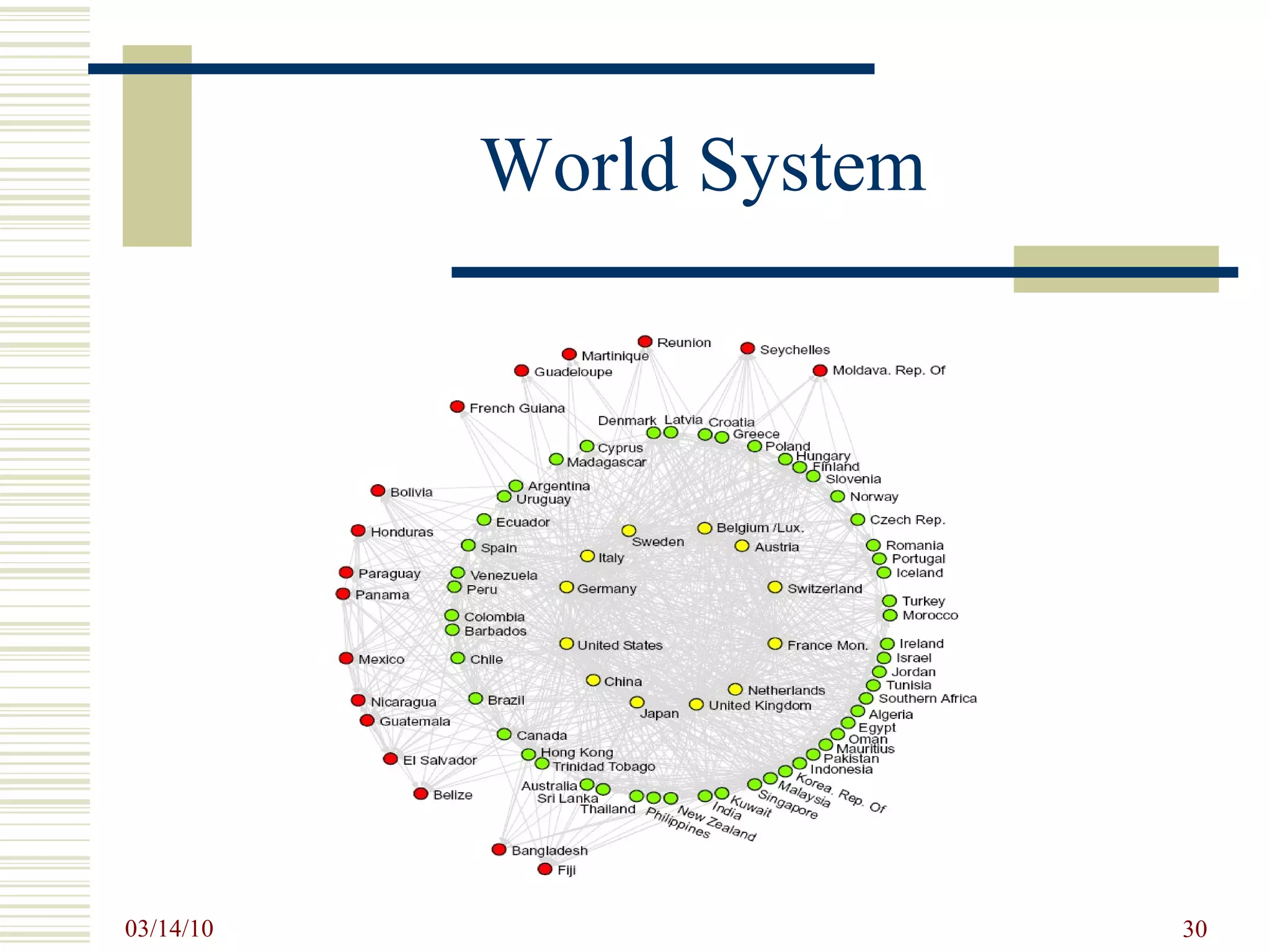
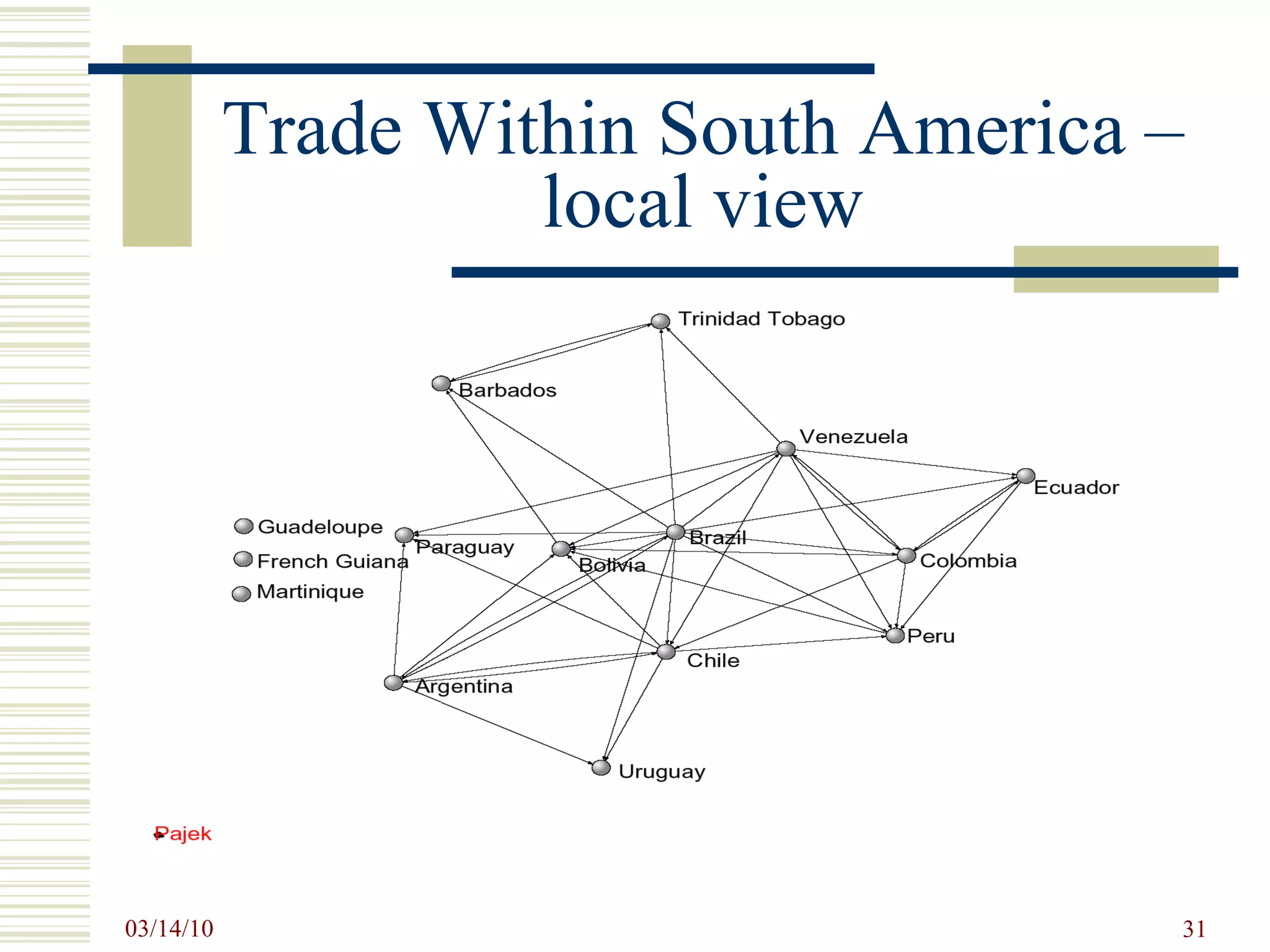
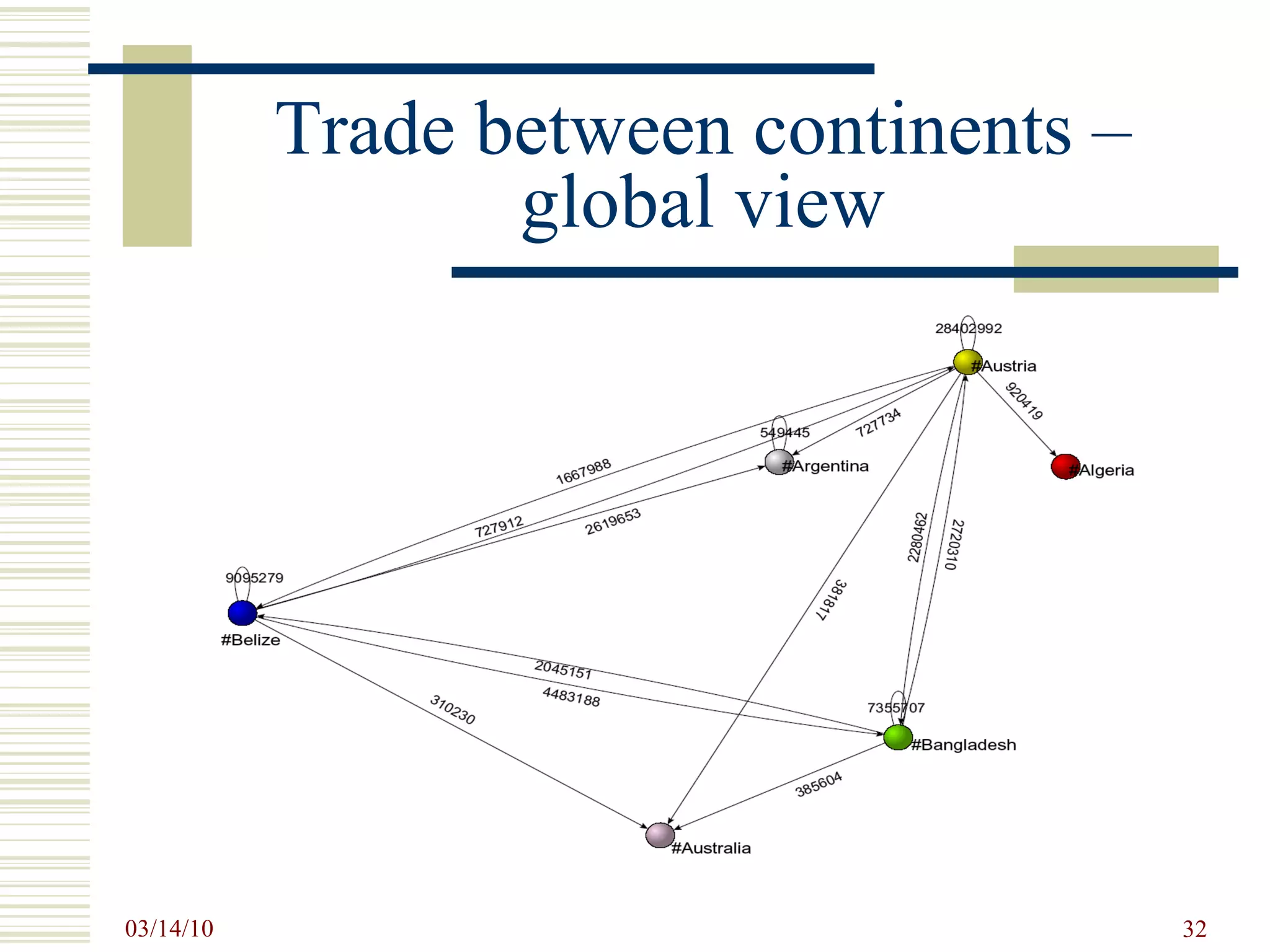
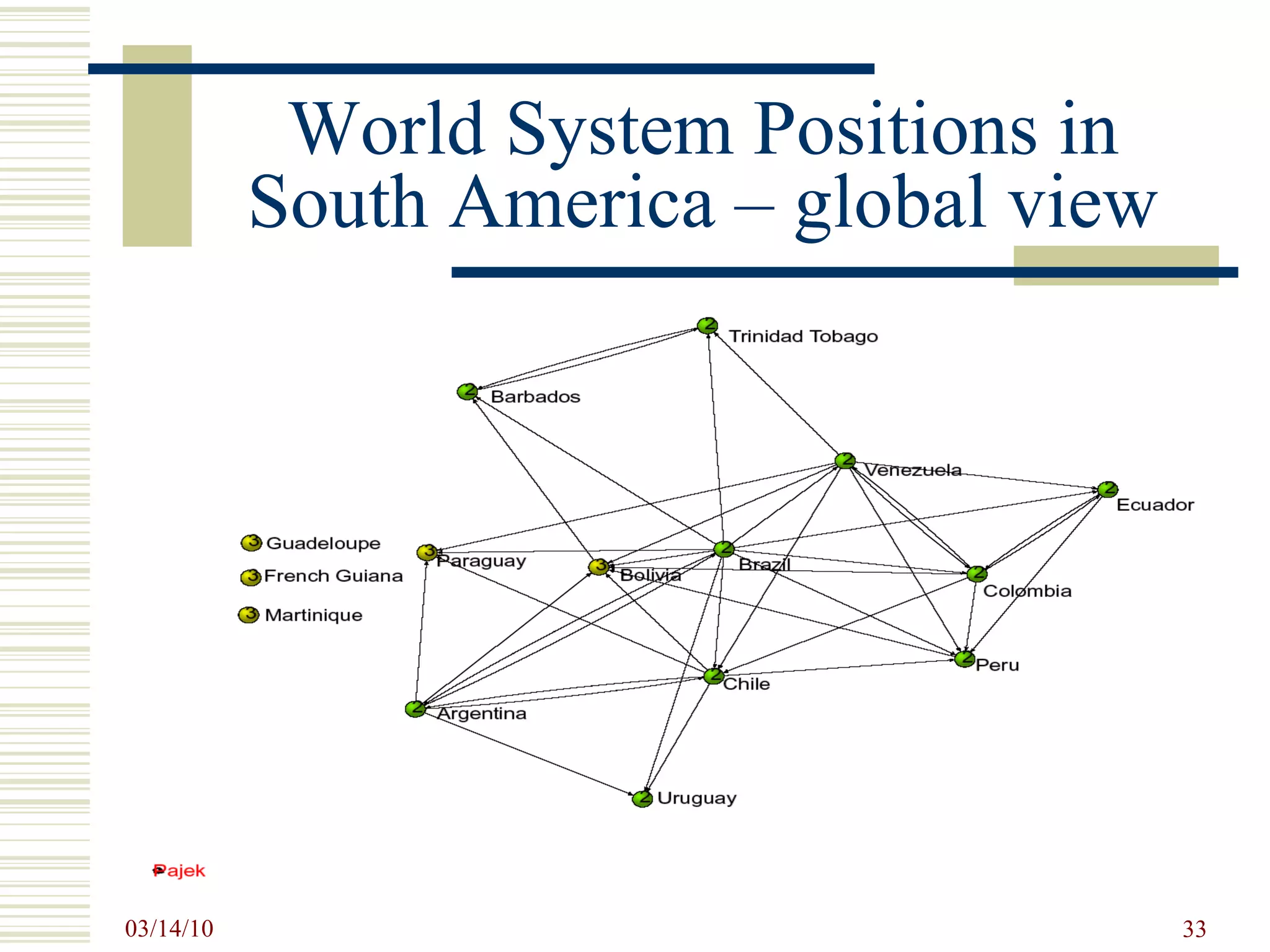
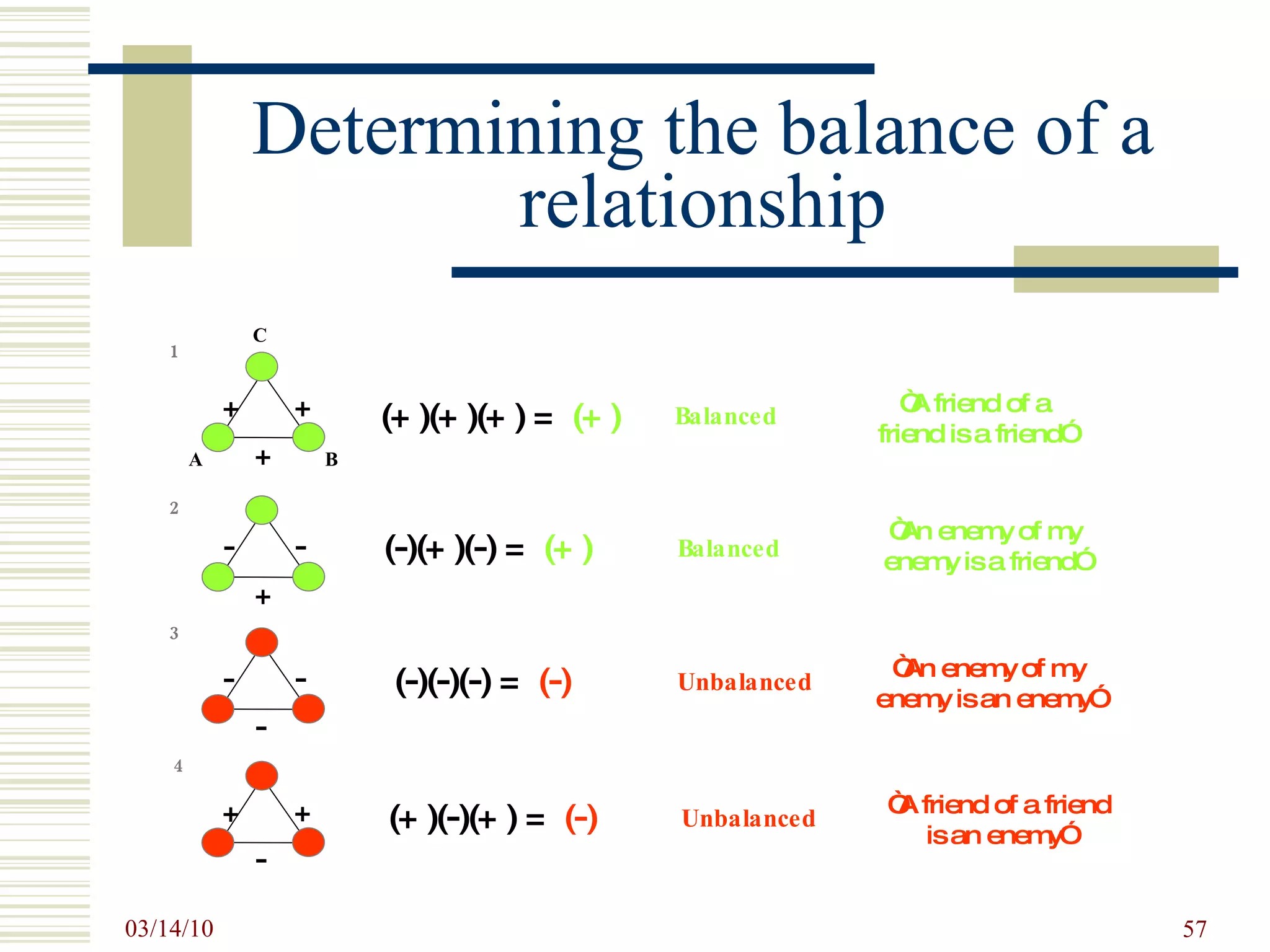
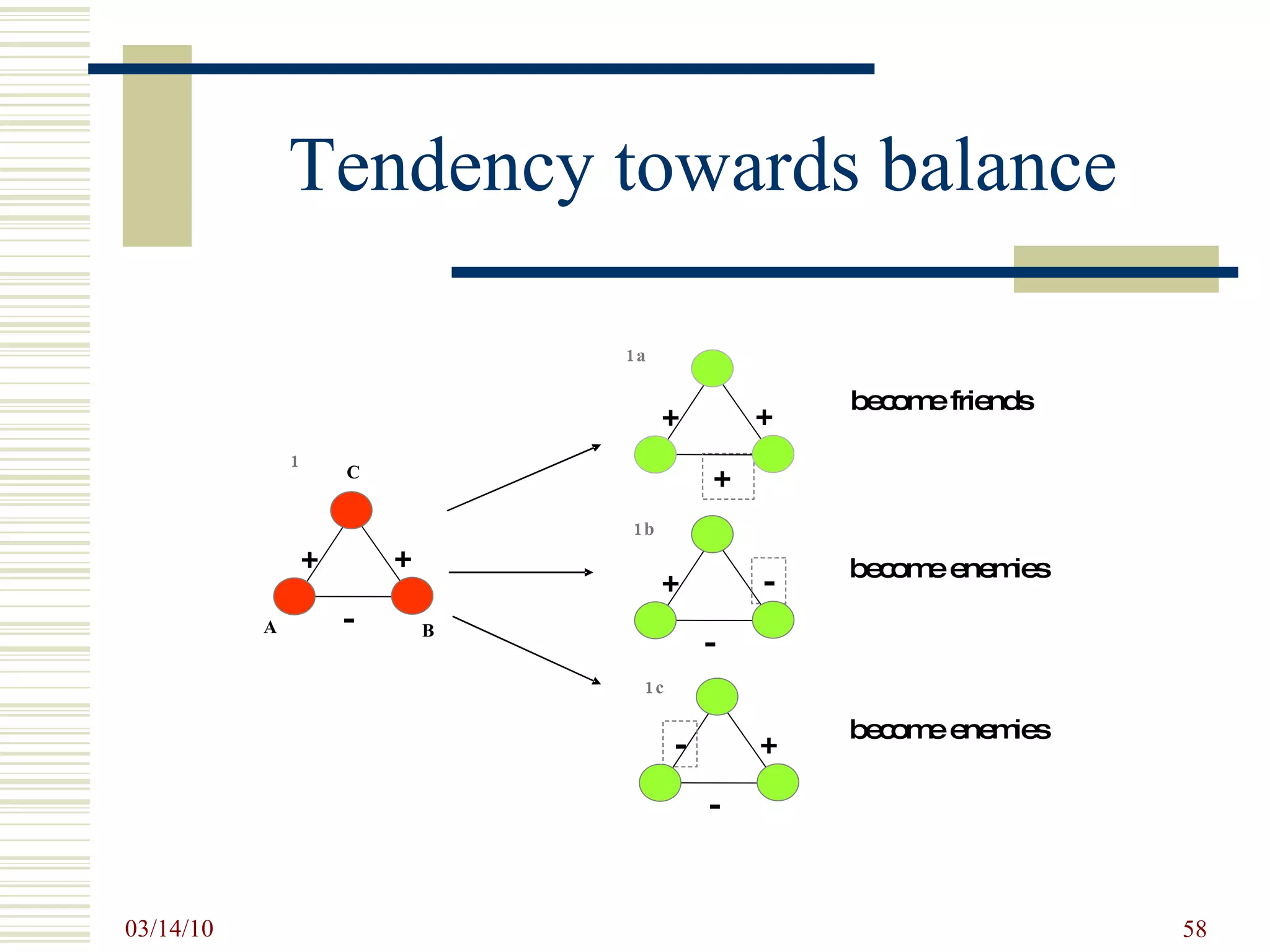
27. SNA Measurements Prevalent SNA measures at the  Individual level: centrality and prestige and roles such as isolates, liaisons, bridges, etc. degree centrality – activity closeness centrality – access to resources betweenness centrality – control eigenvector centrality – overall influence  D yadic level: distance and reachability, structural and other notions of equivalence, and tendencies toward reciprocity.  T riadic level: balance and transitivity  S ubset level: cliques, cohesive subgroups, components  N etwork level: connectedness, diameter, centralization, density etc. [Wasserman, S. and K. Faust, 1994, Social Network Analysis. ]

28. Partitions A partition of a networks is a classification or clustering of the vertices in the networks such that each vertex is assigned to exactly one class or cluster.

29. World System Go through the “World System” example Open the trade network and energize the positions of the core countries only. Hint: create a new partition where core countries belong to class zero and others to class one or higher and energize it with Fix selected networks command.

30. World System

31. Trade Within South America – local view

32. Trade between continents – global view

33. World System Positions in South America – global view

34. Contextual view

35. World System GDP Vector

36. Fun with partitions There are several partition exercises we will work on now.

37. File: Attiro.net Load Attiro.net

38. Visiting Ties in Attiro

39. Density and Degree Density is the number of lines in a simple network expressed as a proportion of the maximum number of lines. A complete network is a network of maximum density. The degree of a vertex is the number of lines incident with it.

40. Degree measures Info>Network>General Net>Transform>Arcs>Edges>All File>Network>Save Net>Partitions>Degree Info>Partition Partition>Make Vector Info>Vector

41. Exercise – Compare Networks Compare the network SanJuanSur.net to the Attiro network. Is this network more cohesive?

42. Ajacent, indegree, outdegree Two vertices are adjacent if they are connected by a line. The indegree of a vertex is the number of arcs it receives. The outdegree is the number of arcs it sends.

43. Semiwalks and walks A semiwalk from vertex u to vertex v is a sequence of lines such that the end vertex of one line is the starting vertex of the next line and the sequence starts at vertex u and ends at vertex v. A walk is a semiwalk with the additional condition that none of its lines are an arc of which the end vertex is the arc’s tail.

44. Paths and Semipaths A semipath is a semiwalk in which no vertex in between the first and last vertex of the semiwalk occurs more than once. A path is a walk in which no vertex in between the first and last vertex of the walk occurs more than once.

45. Connection A network is (weakly) connected if each pair of vertices is connected by a semipath. A networks is strongly connected if each pair of vertices is connected by a path.

46. Weak and Strong Components A (weak) component is a maximal (weakly) connected subnetworks. A strong component is a maximal strongly connected subnetwork.

47. Find components: Attiro.net Net>Components>Strong (raise number to eliminate uninteresting components) Draw>Draw-Partition Net>Components>Weak

48. Cores A k-core is a maximal subnetwork in which every vertex has at least degree k within the subnetwork.

49. K-cores in Attiro visting network

50. Extracting k-cores Net>Partitions>Core>Input,Output,All Operations>Extract from Network>Partition Net>Components>Strong

51. Exercise: Extract k-cores Determine the k-cores in the network ExerciseII.net and extract the 4-core from the network.

52. Cliques A clique is a maximal complete subnetwork containing 3 vertices or more.

53. Clique detection (Attiro.net) Net>Transform>Arcs>Edges>All Nets>First Network,Second Network 2 nd : triad_undir.net Nets>Fragment (1 in 2)>Find Nets>Fragment (1 in 2)>Options Extract Subnetwork checked File>Hierarchy>Edit Info>Partitions

54. Signed Graph A signed graph is a graph in which eash line carries either a positive or a negative number.

55. Cycles, semicycles A cycle is a closed path. A semicycle is a closed semipath. A (semi)-cycles is balanced if it does not contain an uneven number of negative arcs.

56. Eight possible triadic constellations

57. Determining the balance of a relationship

58. Tendency towards balance

59. Clustering A cycle or semicycle is clusterable if it does not contain exactly one negative arc. A signed graph is clusterable if it can be partitioned into clusters such that all positive ties are contained within clusters and all negative ties are situated between clusters.

60. Balance in the Monastery

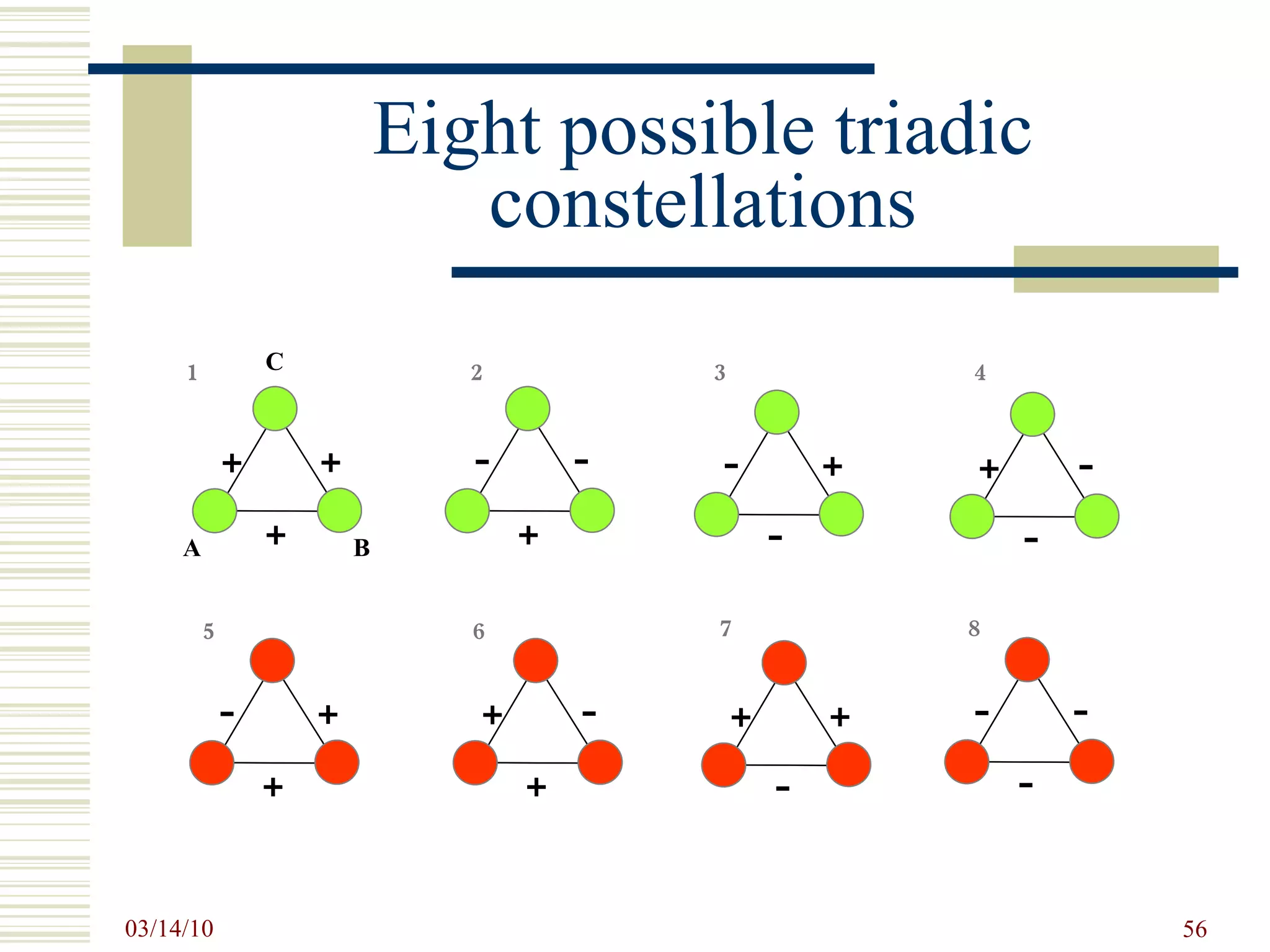
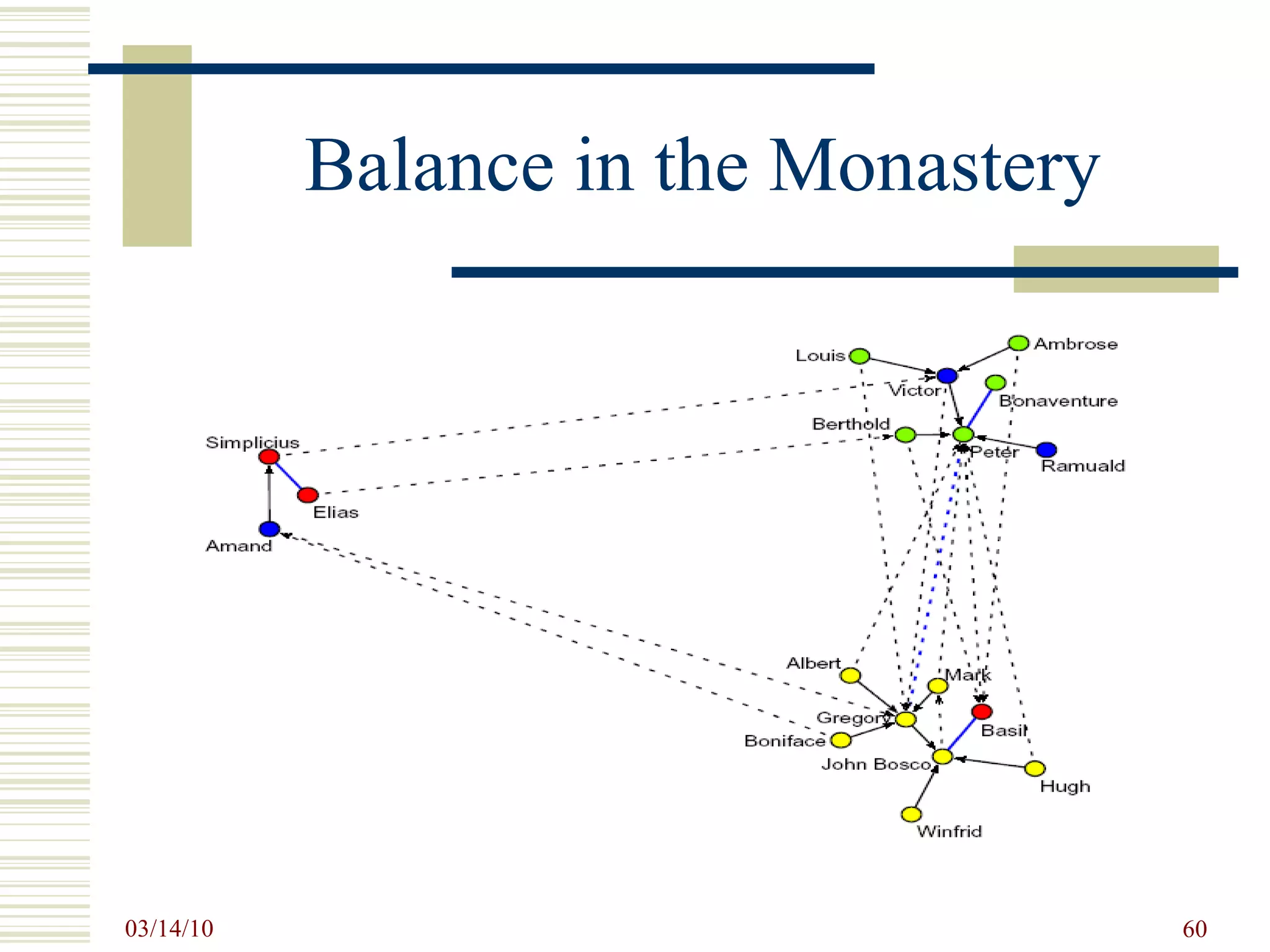
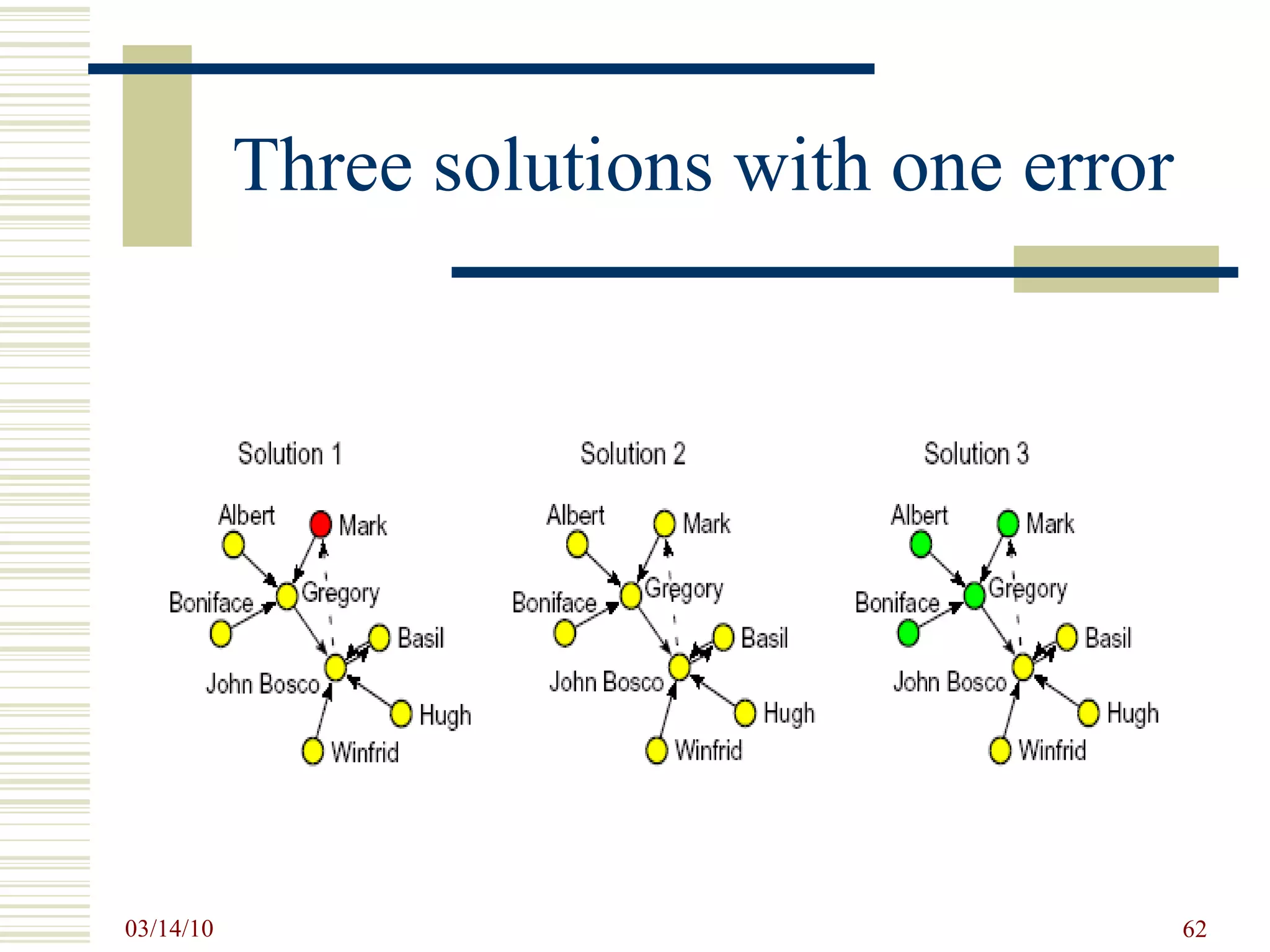
61. Computing Balance [Draw]>Options>Values of Lines>Similarities Partitions>Create Random Partition (3 clusters) Operations>Balance (>100) – try several times.

62. Three solutions with one error

63. Balance over time Groups tend towards balance over time Networks over time are called “longitudinal”

64. Networks in time Net>Transform>Generate in Time Use 2 - 4 Previous Next Options Previous/Next>Apply to Options Previous/Next>Optimize Layouts

65. Affiliation Network Use: scotland.paj What does it mean?

66. Affiliations One mode network Two mode network

67. Experiment Create one mode of directors. Create one mode of banks. Check out [Draw]>Options>Lines>Different Widths

68. The Sawmill

69. Degree centrality The degree centrality of a vertex is its degree Degree centralization of the network is the variation in the degrees of verticies divided by the maximum degree variation which is possible in a network of the same size.

70. Distance A geodesic is the shortest path between two verticies The distance from vertex u to vertex v is the length of the geodesic from u to v.

71. Closeness The closeness centrality of a vertex is the number of other vertices divided by the sum of all distances between the vertex and all others. Closeness centralization is the variation in the closeness centrality of vertices divided by the maximum variation in closeness centrality scores possible in a network of the same size.

72. Closeness application Net>Transform>Edges>Arcs Net>Partitions>Degree Net>Transform>Remove>multiple lines Net>Transform>Remove>loops Net>k-neighbours Net>Paths between 2 vertices>All shortest Net>Vector>Centrality>Closeness

73. Two more operations Net>Paths between 2 vertices>All Shortest Net>Vector>Centrality>Closness

74. Exercise What will happen to the network if Juan (HM-1) disappears? Remove the vertex, compare closeness centrality and centralization and interpret the results.

75. Betweenness The betweenness centrality of a vertex is the proportion of all geodesics between pairs of other vertices that include this vertex. Betweenness centralization is the vairation in the betweenness centrality of vertices divided by the maximum vairiation in betweenness centrality scores possible in an network of the same size.

76. Betweenness Application Net>Vector>Centrality>Betweeness

77. Exercise Compute and draw the betweenness of the sawmill network.

78. Bridges A bridge is a line whose removal increases the number of components in the network. Deleting a vertex from the network means that the vertex and all lines incident with the vertex are removed from the network. A cut-vertex is a vertex whose deletion increase the number of components in the network.

79. Bi-Components A bi-component is a component of minimum size 3 that does not contain a cut-vertex.

80. Strike Network

81. Bi-Components Net>Components>Bi-Components Use “2” to identify bridges “Vertices belonging to …” Isolates: 0, more than one (bridges): 9999998 Articulation points: number of bridges to which a node belongs (0 – 0, 1 – 1, …)

82. Ego-Networks, Constraint The ego-networks of a vertex contains the vertex, its neighbors, and all lines among the selected vertex.

83. Dyadic Constraint The dyadic constraint on a vertex u exercised by a tie between vertices u and v is the extent to which u has more and stronger ties with neighbors who are strongly connected to vertex v .

84. Structural Holes Net>Vector>Structural Holes Options>Values of Lines>Similarities Info>Vector Vectors>Transform>Multiply By [Draw]Options>Size of Vertices Net>k-neighbors>All (from 1, distance 1) Operations>Extract from Network>Partition (1) [Main]Info>Network>General

85. Structural Holes 2 Net>Vector>Clustering Coefficients>CCI Look at Vector: Clustering Coefficients CC1

86. Constraint Operations>Transform>Remove Lines>Between Clusters Net>Vector>Structural Holes Operations>Brokerage Roles Info>Partition

87. Diffusion Draw->Draw Partition (ModMath.net) Layers> in y direction Move>Fix>y [Draw screen]Options>Transform>Rotate 2D

88. Contagion The adoption rate is the number or percentage of new adoptors at a particular moment. Info>Partition

89. Exposure and Thresholds The exposure of a vertex in a network at a particular moment is the proportion of the neighbors who have adopted at that time. The threshold of an actor is his or her exposure at the time of adoption.

90. Critical Mass The critical mass of a diffusion process is the minimum number of adopters needed to sustain a diffusion process. A threshold lag is a period in which an actor does not adopt although he or she is exposed at the level at which he or she will adopt later.