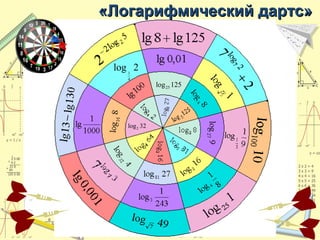
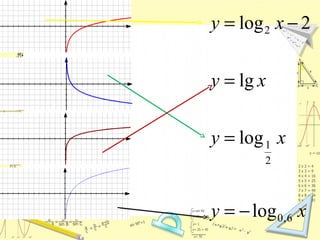
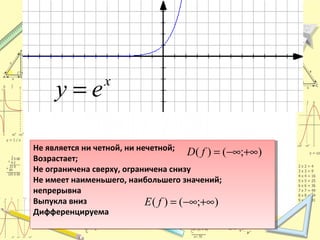
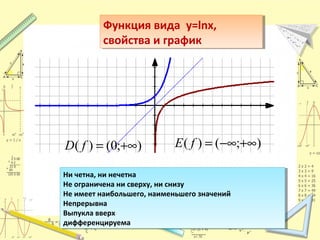
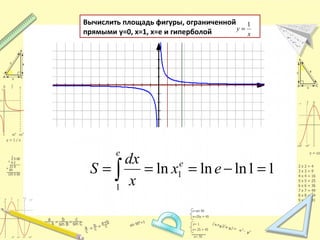
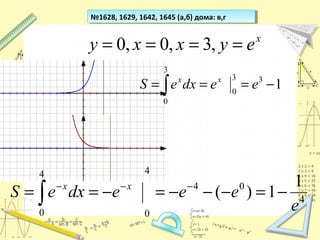
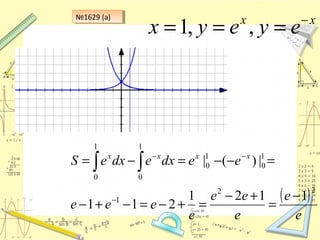
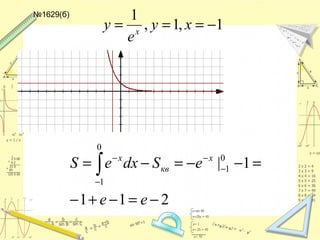
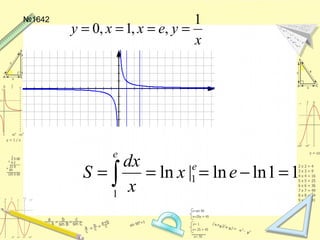
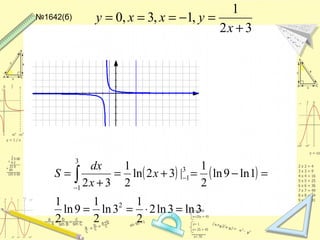
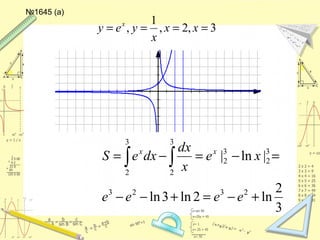
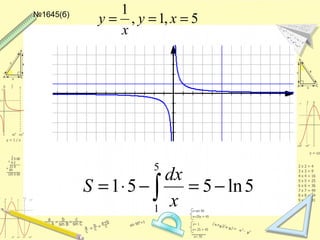
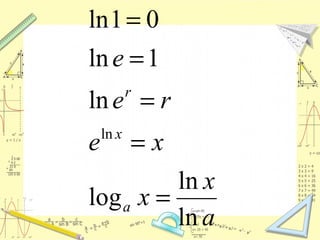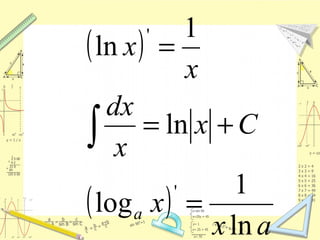Документ обсуждает понятие натурального логарифма, его свойства и взаимное расположение графиков функций натурального логарифма и экспоненты. Натуральный логарифм упрощает множество математических формул и находит применение в различных физических и биологических задачах. Приводятся конкретные примеры логарифмических вычислений и задач на производные и интегралы.

1. МатематикМатематик
аа
Натуральные логарифмы
Расширить понятие логарифма, для этого введя
понятие натурального логарифма, выяснить
взаимное расположение графиков функции
натурального логарифма и показательной,
научиться использовать свойства для вычисления
натуральных логарифмов

2. «Логарифмический дартс»«Логарифмический дартс»
125log25
2log
4
1
32log2

3. 1 11
2 12
3 13
4 14
5 15
6 16
7 17
8 18
9 19
10
7
5 5log
2log11 =x
4log
2
1
3log5 −=x
1000lg
2log2 =x
1lg −=x
14log =x
625
1
log5
2log 2.0 =x
1lg
17log =x
x=16log2
4
7 7log
3125log
5
1
3
343
1
log =x
2log6 −=x
49log7
4256log =x
7
121
125
1
0,04
4
0,1
3
-4
4
-2
0
-5
7
4
2
4
4
36
1
-5

4. xy
xy
xy
xy
6,0
2
1
2
log
log
lg
2log
−=
=
=
−=

5. x
ey =
Не является ни четной, ни нечетной;
Возрастает;
Не ограничена сверху, ограничена снизу
Не имеет наименьшего, наибольшего значений;
непрерывна
Выпукла вниз
Дифференцируема
Не является ни четной, ни нечетной;
Возрастает;
Не ограничена сверху, ограничена снизу
Не имеет наименьшего, наибольшего значений;
непрерывна
Выпукла вниз
Дифференцируема
);()( +∞−∞=fЕ
);()( +∞−∞=fD

6. Функция Производная
x
ey 2=
x
ey 2=
x
ey 2
= x
ey 2
2=
xey x
−= 1−= x
ey
23
xey x
−= xey x
23 3
−=
x
e
y 





=
1 x
ey −=

7. ∫ += Cedxe xx
1
1
+
+
n
xn
2
1
x
x
1
−
x
1
)0(;2 >xx
x2
sin
1
n
x
-ctg x-ctg x
x2
cos
1 tg xtg x
cos xcos x -sin x-sin x
sin xsin x cos xcos x
)(
1
bkxF
k
y +=
y= f(kx+b)y= f(kx+b)
y=f(x)+g(x)y=f(x)+g(x) Y=F(x)+G(x)Y=F(x)+G(x)
y=kf(x)y=kf(x) Y=kF(x)Y=kF(x)

8. ∫
a
b
dxxf )( =F(b) – F(a).
∫ =
a
b
a
b
xFdxxf |)()(

9. ∫ dxex
3 Cex
+3
∫
−
dxe x 32 Ce x
+−32
2
1
∫ 2
x
dx
C
x
+−
1
∫ + dxxex
)2sin( Cxex
+− 2cos
2
1

10. Логарифм по основанию е
называется натуральным
логарифмом
Логарифм по основанию е
называется натуральным
логарифмом
0,lnlog >= bbbe
Десятичные логарифмы для наших
потребностей являются весьма
удобными. Однако при изучении
высшей математики более удобными
оказываются логарифмы по основанию
е = 2,718281828... (см. § 134, ч. 1).
Употребление этих логарифмов
позволяет значительно упростить
большое количество математических
формул. Логарифмы по основанию е
получаются при решении многих
физических задач и естественным
образом входят в математическое
описание некоторых химических,
биологических и других процессов.
Этим и объясняется их название
«натуральные логарифмы».
Натуральный логарифм числа а
обозначается ln а. Сейчас имеются
достаточно полные таблицы
натуральных логарифмов.
Десятичные логарифмы для наших
потребностей являются весьма
удобными. Однако при изучении
высшей математики более удобными
оказываются логарифмы по основанию
е = 2,718281828... (см. § 134, ч. 1).
Употребление этих логарифмов
позволяет значительно упростить
большое количество математических
формул. Логарифмы по основанию е
получаются при решении многих
физических задач и естественным
образом входят в математическое
описание некоторых химических,
биологических и других процессов.
Этим и объясняется их название
«натуральные логарифмы».
Натуральный логарифм числа а
обозначается ln а. Сейчас имеются
достаточно полные таблицы
натуральных логарифмов.

11. a
x
x
xe
re
e
a
x
r
ln
ln
log
ln
1ln
01ln
ln
=
=
=
=
=

12. Функция вида y=lnx,
свойства и график
Функция вида y=lnx,
свойства и график
);0()( +∞=fD );()( +∞−∞=fE
Ни четна, ни нечетна
Не ограничена ни сверху, ни снизу
Не имеет наибольшего, наименьшего значений
Непрерывна
Выпукла вверх
дифференцируема
Ни четна, ни нечетна
Не ограничена ни сверху, ни снизу
Не имеет наибольшего, наименьшего значений
Непрерывна
Выпукла вверх
дифференцируема

13. ( )
( )
ax
x
Cx
x
dx
x
x
a
ln
1
log
ln
1
ln
'
'
=
+=
=
∫

14. ( ) 1,53ln −=+= xxy
( )
5,1
5)1(3
3
)1(
53
3
53
1
3)53ln(
'
''
=
+−
=−
+
=
+
⋅=+=
y
xx
xy
xy 2log=
2ln
1'
x
y =
1633, 1634, 1635, 1636(а,б)
Дома: в,г
1633, 1634, 1635, 1636(а,б)
Дома: в,г

15. №1633
( ) ( )
xxx
x
xxxy
xxxxy
xxy
+=⋅+=
+=
=
ln2
1
ln2
lnln''
ln
2'
'22
2
( ) ( ) ( )
( )
( )
( ) ( )22
2
''
"
1
ln1
1
ln1
1
1
1ln1ln
1
ln
+
−+
=
+
−+⋅
=
+
+−+
=
+
=
xx
xxx
x
xx
x
x
xxxx
y
x
x
y

16. №1634
x
e
xey
xey
x
x
x
+=
=
ln
ln
'
x
x
y
xxy
2cos2
3
2sinln3
'
+=
+=

17. №1635
8
1
1
7
1
,ln
'
'
0
=
+=
=+=
y
x
y
xxxy
222'
22'
0
3
43
ln3
,ln
eeey
xxxy
exxxy
=+=
+=
==

18. №1636 ( )
3
1
1
3
4
4
1
1
1
1
1
22
2
4
1
,22ln
'
'
0
==
−
=
+
=
+
=
−=+=
y
xx
y
xxy
( )
2
1
2
25
2
2,25ln
'
0
−=−=
−
−=
=−=
x
y
xxy

19. Составить уравнение касательной к графику
функции y=lnx в точке x=e
Составить уравнение касательной к графику
функции y=lnx в точке x=e
( )( ) )( 000
'
xfxxxfy +−=
( )
e
x
e
x
ex
e
y
e
xf
x
xf
exf
=+−=+−=
=
=
==
111
1
1
)(
1
)('
1ln)(
0
'
0
№1623,1637,16
41 (а,б)
в,г - дома
№1623,1637,16
41 (а,б)
в,г - дома

20. ( )
11
6
ln
5
1
11ln6ln
5
1
65ln
5
1
65
0
1
0
1
−=−−
=+−−=
+−∫−
−
x
x
dx
№1642, 1643№1642, 1643
∫ =−==
2
1
2
1
2ln1ln2lnln x
x
dx
( )
∫
+−
=−+−=+=





+2
1 2
22
1
2ln
1ln2lnln
1
ee
eexedx
x
e xx
( ) ( )
3ln
2
1
3
9
ln
2
1
3ln9ln
2
1
32ln
2
1
32
6
3
6
3
=
=−=−=
−∫ x
x
dx

21. Вычислить площадь фигуры, ограниченной
прямыми y=0, x=1, x=e и гиперболой x
y
1
=
∫ =−===
e
e
ex
x
dx
S
1
1 11lnlnln

22. №1628, 1629, 1642, 1645 (а,б) дома: в,г№1628, 1629, 1642, 1645 (а,б) дома: в,г
x
eyxxy ==== ,3,0,0
∫ −===
3
0
33
0
1eedxeS xx
4
04
4
0
4
0
1
1)(
e
eeedxeS xx
−=−−−=−== −−−
∫

23. №1629 (а)№1629 (а)
xx
eyeyx −
=== ,,1
( )
e
e
e
ee
e
eee
eedxedxeS xxxx
22
1
1
0
1
0
1
0
1
0
1121
211
|)(|
−
=
+−
=+−=−+−
=−−=−=
−
−−
∫ ∫

24. №1629(б)
1,1,
1
−=== xy
e
y x
211
1|
0
1
0
1
−=−+−
=−−=−= ∫−
−
−−
ee
eSdxeS x
кв
x

25. №1642
x
yexxy
1
,,1,0 ====
11lnln|ln 1
1
=−=== ∫ ex
x
dx
S e
e

26. №1642(б)
32
1
,1,3,0
+
=−===
x
yxxy
( ) ( )
3ln3ln2
2
1
3ln
2
1
9ln
2
1
1ln9ln
2
1
|32ln
2
1
32
2
3
1
3
1
=⋅==
=−=+=
+
= ∫−
−x
x
dx
S

27. №1645 (а)
3,2,
1
, ==== xx
x
yey x
3
2
ln2ln3ln
|ln|
2323
3
2
3
2
3
2
3
2
+−=+−−
=−=−= ∫ ∫
eeee
xe
x
dx
dxeS xx

28. №1645(б)
5,1,
1
=== xy
x
y
5ln551
5
1
−=−⋅= ∫ x
dx
S

29. Задание на каникулы:
Создать справочник по формулам (лучше
напечатать, чтобы можно было размножить),
презентация, видеоролик и т.п.
1.Тригонометрические формулы
2.Тригонометрические уравнения (общий вид,
частные случаи, методы решения)
3.Производная
4.Применение производной к исследованию
функций
5.Функции, свойства, графики, преобразования
6.Первообразная и интеграл
7.Показательные уравнения и неравенства
8.Логарифмические уравнения и неравенства
9.Степени и корни
10.Системы уравнений
11.Основные типы задач
12.РЕШАТЬ ВАРИАНТЫ ЕГЭ
Задание на каникулы:
Создать справочник по формулам (лучше
напечатать, чтобы можно было размножить),
презентация, видеоролик и т.п.
1.Тригонометрические формулы
2.Тригонометрические уравнения (общий вид,
частные случаи, методы решения)
3.Производная
4.Применение производной к исследованию
функций
5.Функции, свойства, графики, преобразования
6.Первообразная и интеграл
7.Показательные уравнения и неравенства
8.Логарифмические уравнения и неравенства
9.Степени и корни
10.Системы уравнений
11.Основные типы задач
12.РЕШАТЬ ВАРИАНТЫ ЕГЭ