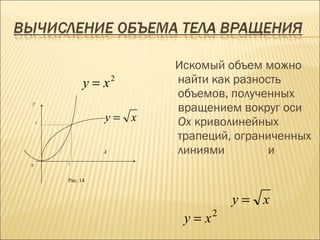
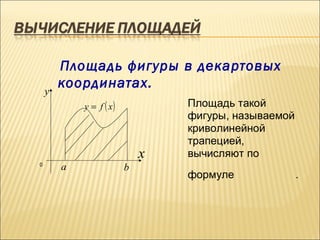
Документ рассматривает методы вычисления площади и объема фигур, ограниченных графиками функций и осью координат. Он описывает теоремы, такие как формула Ньютона-Лейбница и методы интегрирования по частям, а также несобственные интегралы. Включает примеры расчета площадей криволинейных трапеций и объемов тел вращения.

2. Решим задачу о вычислении площади
фигуры, ограниченной графиком функции
y = f ( x)
, отрезками прямых
x = ,a x = и осью Ox.Такую фигуру
b
называют криволинейной трапецией
a b
xi −1 xi

3. Разобьем отрезок на n частей
точками .
При этом криволинейная трапеция разобьется
на элементарных криволинейных
трапеций. Заменим каждую такую
криволинейную трапецию прямоугольником с
основанием , где и
высотой , где -произвольно
выбранная внутри отрезка точка.

4. Площадь прямоугольника будет
равна , а площадь
всей криволинейной фигуры
приблизительно будет равна
сумме площадей всех
прямоугольников:
.

5. Определение.
Выражение , где
, называется
интегральной суммой функции
на отрезке .

6. Определение.
Если существует конечный , не
зависящий ни от способа разбиения отрезка
на части, ни от выбора точек ,
то этот предел называется определенным
интегралом функции на отрезке и
обозначается .

7. Замечание.
С геометрической точки зрения
при равен
площади криволинейной
трапеции

8. Теорема.
Если функция непрерывна на
отрезке , то
существует и конечен, т.е.
существует и конечен .

9. 1. ;
2. ;
3. ;
4. ;

10. 5. ;
6. ;
7. , если .

11. Если функция непрерывна на то
[a, b],
существует такая точка
b
ξ ∈ [a, b],
что
∫
a
f ( x)dx = f (ξ )(b − a ).
y = f (x)
a ξ b

12. Теорема.
Пусть - первообразная функции .
Тогда .
Эту формулу называют формулой
Ньютона-Лейбница, из которой следует,
что для вычисления определенного
интеграла необходимо найти
первообразную подынтегральной функции.

13. x
3 −
Вычислить ∫e 3 dx .
0 3
3 −
x 1
3 − ⋅x
1
− ⋅x  − 1 ⋅3 − ⋅0 
1
∫e 3 dx =∫ e 3 dx = −3e 3 = −3 e 3 − e 3  =
0 0
 
0  
= −3 e( −1
) 1 
− 1 = −3 − 1 = −3
1− e
e  e

14. Теорема (Замена переменной в
определенном интеграле).
Пусть непрерывна на ,а
функция непрерывна вместе
со своей производной на
отрезке , причем ,
. Тогда
.

15. x +1 = t
x +1 = t 2
3 xdx 2 t2 −1
2
∫ = x = t − 1, dx = 2tdt = ∫ 2tdt =
0 x +1 1 t
x = 0, t = 1
x = 3, t = 2
2
( ) ( )
t 
3
 
 − t  = 2 8 − 2  −  1 − 1 =
2 2
2 2
= ∫ 2 t − 1 dt = 2 ∫ t − 1 dt = 2    
 3 
1 1  1  3   3 
8 1  7  4 8
= 2 − 2 − + 1 = 2 − 1 = 2 ⋅ =
3 3  3  3 3

16. Теорема (Интегрирование по
частям в определенном
интеграле).
Если функции , и их
производные и
непрерывны на отрезке , то
.

17. dx
e u = ln x, du = e e dx
∫ ln xdx = x = x ln x 1 − ∫ x =
1 1 x
dv = dx, v = x
e e e
= x ln x1 − ∫ dx = e ln e − ln 1 − x1 = e − e +1 = 1
1

18. Замечание.
не является определенным интегралом.
Считается по определению, что
. Если этот предел
конечен, то , называемый
несобственным, сходится.
Если же этот предел не является конечным, то
интеграл расходится.

19. . Вычислить несобственный интеграл
+∞
xdx
∫
0 x2 + 4
(или установить его расходимость)
. +∞ xdx 1 b
d ( x 2 + 4) 1 b
∫x = ∫ = lim ln( x + 4) =
2
lim
0
2
+4 2 b→+∞ 0 x +4
2
2 b→+∞ 0
1
= lim (ln(b 2 + 4) − ln 4) = ∞
2 b→+∞
Этот несобственный интеграл расходится.

20. Несобственный интеграл
+∞
dx
∫ x2 + 4 =
0
1 b 1 π π
= lim arctg = arctg (+∞) = =
b →+∞ 2 2 2 2 ×2 4

22. Площадь фигуры в декартовых
координатах.
y
y = f ( x) Площадь такой
фигуры, называемой
криволинейной
трапецией,
x вычисляют по
0
a b
формуле .

23. Площадь фигуры, ограниченной графиками непрерывных
функций , , и двумя прямыми
и определяется по формуле

24. В случае параметрического задания
кривой, площадь фигуры, ограниченной
прямыми x = a, x = ,b осью Ох и кривой
x = ϕ (t ), y = ψ (t ),вычисляют по
формуле t2
S = ∫ψ (t )ϕ ′(t )dt ,
где пределы интегрирования определяют из
. t1
уравнений .
a = ϕ (t1 ), b = ϕ (t 2 )

25. Площадь полярного сектора вычисляют
по формуле
β
1 2
S = ∫ r (ϕ )dϕ
2α
.
r = r (ϕ )
β
α

26. Вычислить площадь фигуры, ограниченной
линиями и y = − x 2 − 2x + 3
y = x 2 −1

27. Получим
[( − 2 x + 3) − ( x − 1)]dx = ∫ ( − 2 x )
1 1
2
S = ∫ −x 2 2
− 2 x + 4 dx =
−2 −2
1
( x
) 
1 3 2
x
= −2 ∫ x + x − 2 dx = − 2
2
+ − 2x  =
−2  3 2 
  −2
 1 1   8 4  1 1 8 
= −2  + − 2  −  − + + 4  = −2 + − 2 + − 6  =
 3 2   3 2  3 2 3 
 1  9
= −2 3 − 8 +  = −2 −  = 9
 2  2

28. x2 y2
Найти площадь эллипса 2
+ . Параметрические
2
=1
уравнения эллипса a b
x = a cos t , y = b sin t. 0
S = 4 ∫ b sin t (− a sin t )dt =
у π /2
π /2 π /2
b 1 − cos 2t
х = 4ab ∫ sin tdt = 4ab
2
∫ dt =
о a 0 0
2
1 1 π /2 π
= 4ab(t − sin 2t ) 0 = 2ab = π ab.
2 2 2

29. Площадь фигуры, ограниченной
лемнискатой Бернулли r = a cos 2ϕ
2 2
и лежащей вне круга радиуса : a
r=
2
π /6 π /6 2 π /6
1 1 a 1 2 1 2
∫ a cos 2ϕdϕ − 2 ∫ dϕ = ( a sin 2ϕ − a ϕ ) =
2
2 0 0
2 4 4 0
1 2 π π a2 3 π a2 π
= a (sin − ) = ( − )= ( 3− )
4 3 6 4 2 6 8 3
a2 π
S= ( 3− )
2 3

30. Если кривая задана параметрическими
уравнениями x = ϕ (,t ) y = ψ,( то длина ее
t)
дуги
t2
l= ∫ (ϕ ′( t ) ) 2 + (ψ ′( t ),) 2 dt
t1
где t ,t –значения параметра,
1 2
соответствующие концам дуги .

31. Если кривая задана уравнением
b
y = ,f ( x)
то l = 1 +( f ′( x )) 2 где a, b–абсциссы начала
∫ дуги
и конца
a
, dx
. ( a < b)
Если кривая задана уравнением
d
x = g ( y ), то l = ∫ 1 + ( g ′( y ) ) 2 dy , где c, d–
ординаты начала и cконца дуги (c < d )

32. Если кривая задана уравнением в полярных
координатах , то ρ = ρ (ϕ )
β
l= ∫ ( ρ (ϕ ) ) 2 + ( ρ ′(ϕ ) ) 2 dϕ
α
,
где α , β–значения полярного угла,
соответствующие концам дуги .

33. 3
Вычислить длину дуги кривой y= x
от точки O( 0,0)до B( 4,8)
.
3 ′
x2  = 3 x1
y′ =   2
  2 , тогда
4 4
9 4 9  9 
l= ∫
0
1 + x dx =
4 9 ∫ 1 + xd  1 + x ÷ =
4  4 
0
3
4 2 9  8
( )
2 4
= × 1 + x ÷ = 10 10 − 1
9 3 4  0 27

34. Объем тела, образованного вращением
вокруг оси Ox криволинейной трапеции,
ограниченной кривой y = f ( ,xотрезком оси
)
абсцисс и прямыми ≤ b
a≤x ,
вычисляется поaформуле
x = ,x = b
b
.
∫ ( f ( x) )
2
Vx = π dx
a

35. Объем тела, образованного вращением
вокруг оси Oy фигуры, ограниченной кривой
= g( y)
,xотрезком оси ординат и
прямыми c ≤ y ≤ d , вычисляется поcформуле
y = ,y = d
d
Vy = π ∫ ( g ( y ) ) 2 dy
.
c

36. Искомый объем можно
y = x2 найти как разность
объемов, полученных
вращением вокруг оси
y
1
y= x Ox криволинейных
трапеций, ограниченных
А линиями и
0 1
Рис. 14
y= x
2
y=x

37. 1 1
Тогда
∫ ( x ) dx − π ∫ ( x ) dx =
2 2 2
Vx = π
0 01
1 1 2 5 1
x x
∫ ∫
= π xdx − π x dx = π ⋅ −π ⋅
4
=
0 0
2 5
0 0
π π 3π
= − =
2 5 10