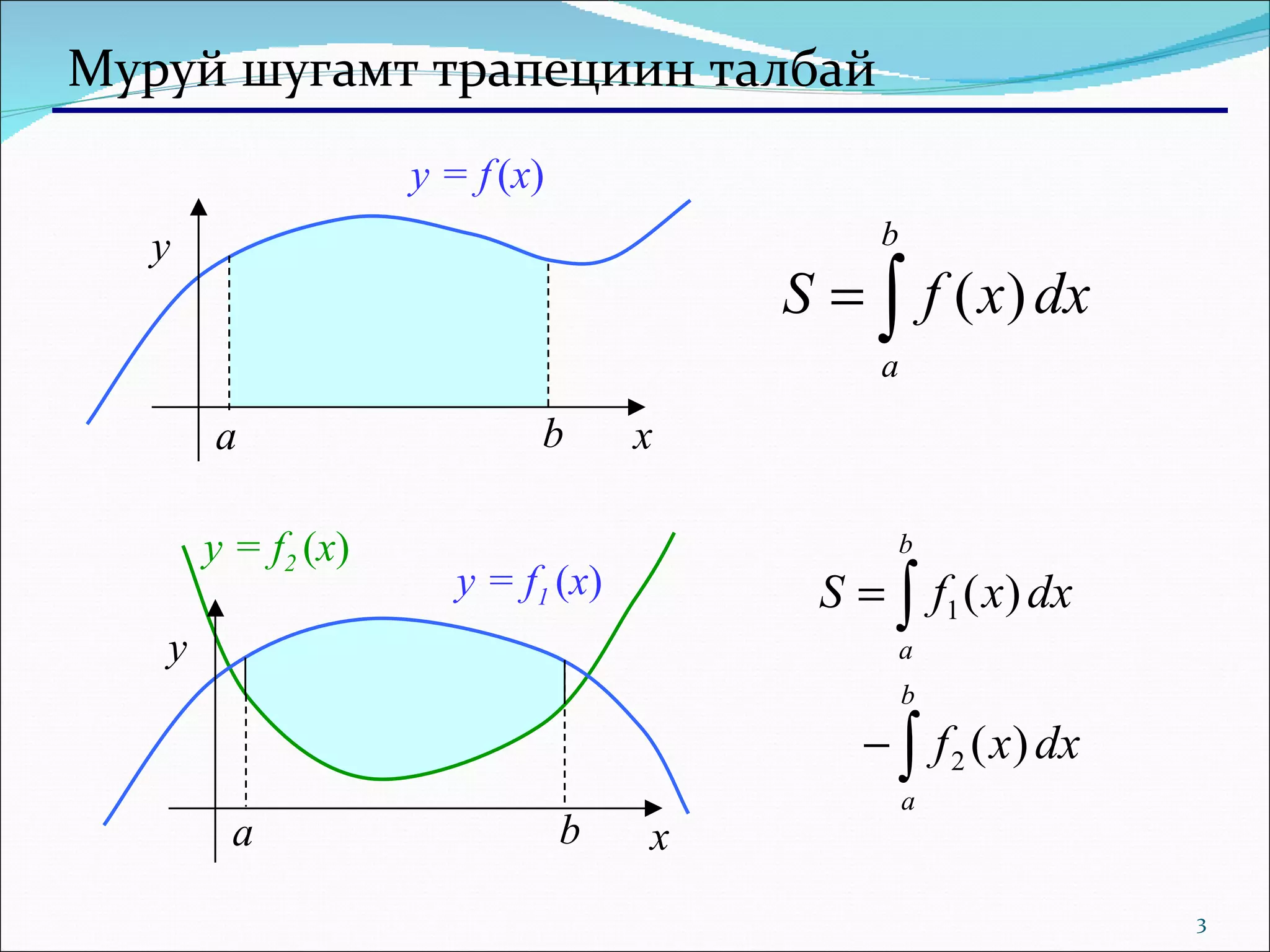
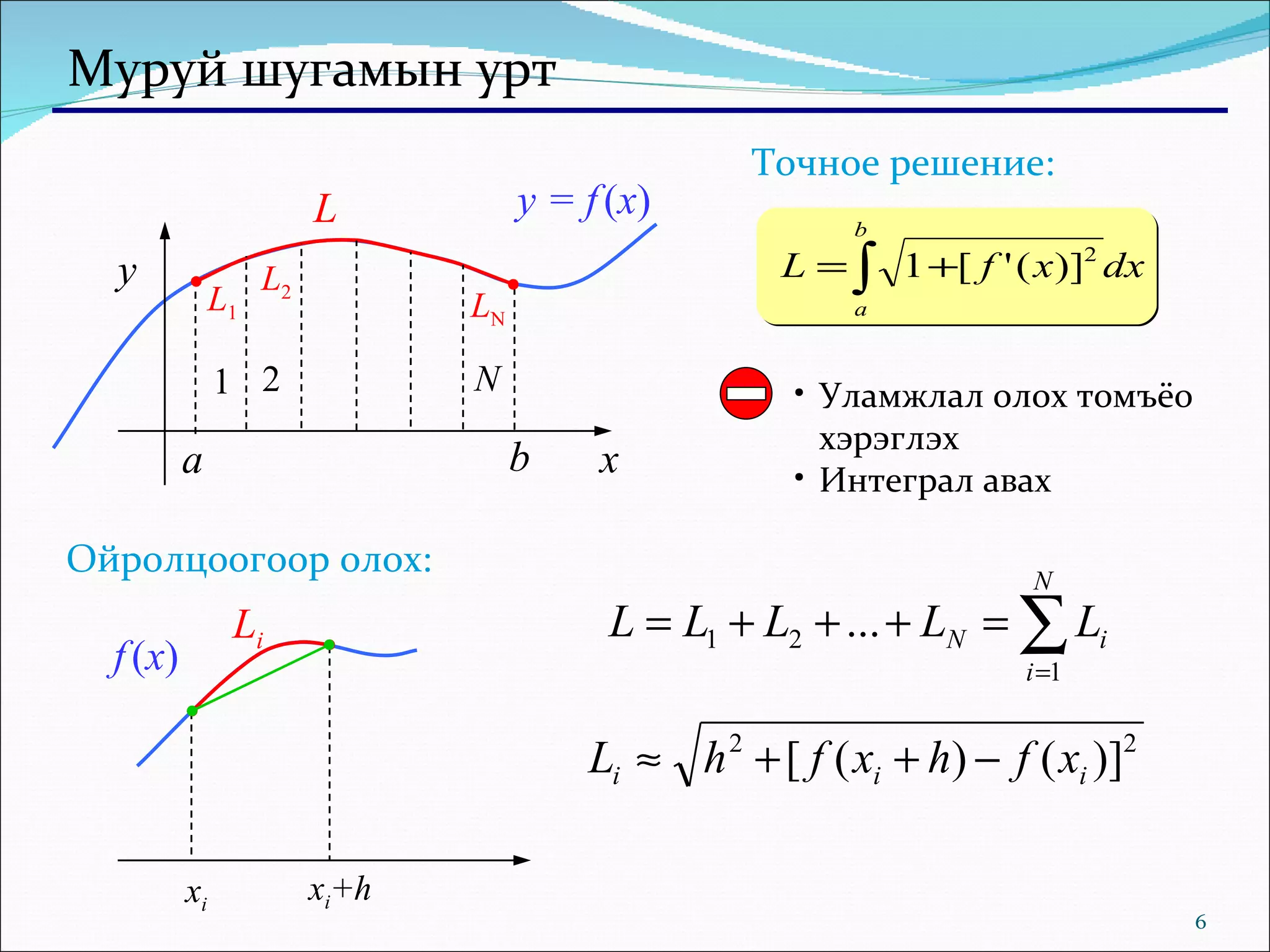
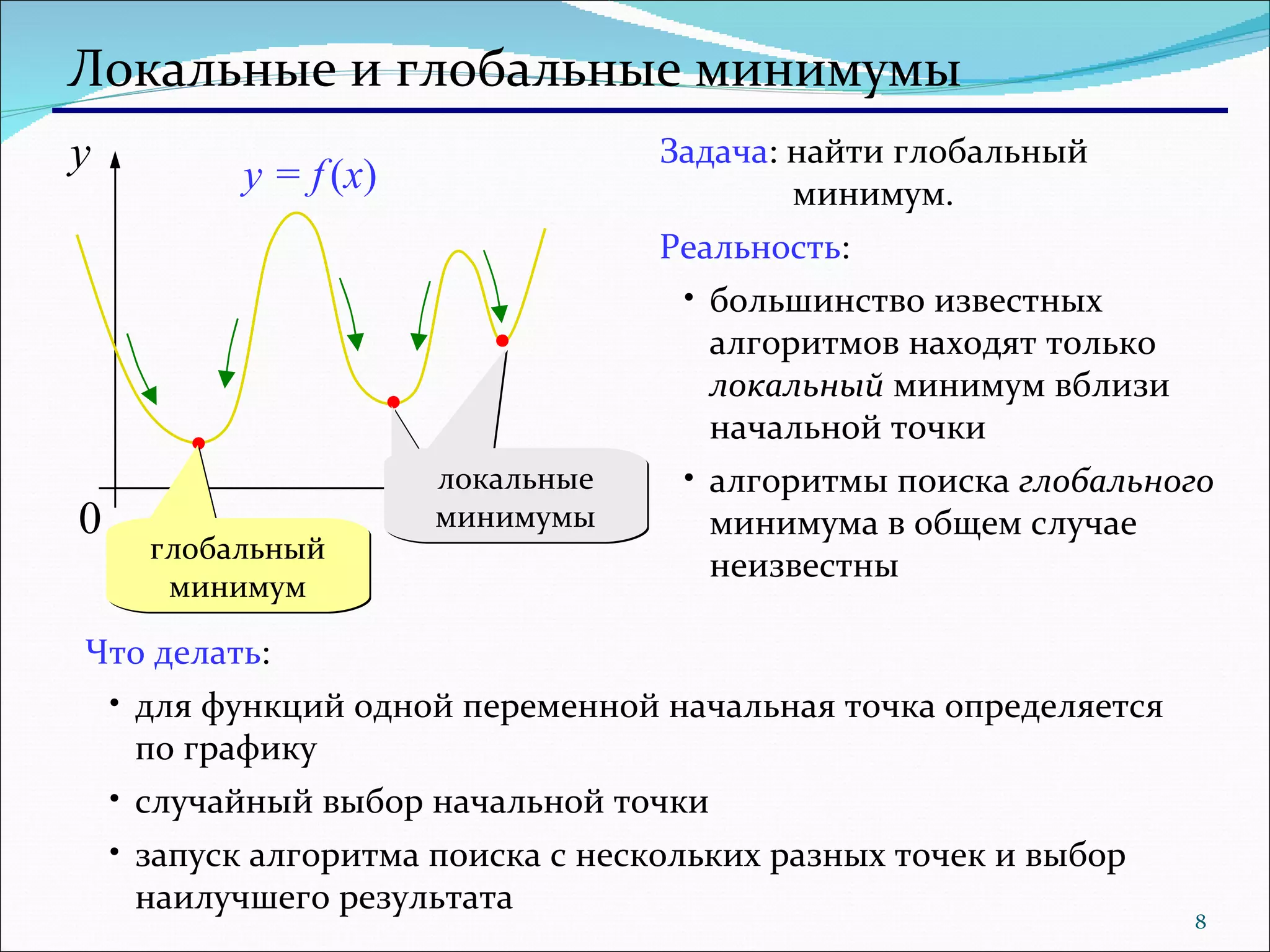
Документ обсуждает методы численного интегрирования и оптимизации, включая вычисление площади под кривой и нахождение локальных и глобальных минимумов функций. Приводятся примеры алгоритмов, таких как метод сжатия интервала и «почти половинного» деления. Обсуждаются проблемы, связанные с выбором начальной точки и находкой глобального минимума.

1. 21 school of UB sity

2. . Талбайг тооцоолох (интеграла) © К.Ю. Поляков, 2008-2009

3. Муруй шугамт трапеции н талбай x y b a y = f ( x ) x y b a y = f 1 ( x ) y = f 2 ( x )

4. Тэгш өнцөгтийн арга y = f 1 ( x ) y = f 2 ( x ) S 1 S 2 S 3 S 4 float Area () { float x, S = 0, h=0.001; for ( x = x1; x < x2; x += h) S += h*(f1(x) – f2(x)); return S; } for ( x = x1; x < x2; x += h ) S += f1(x) – f2(x); S *= h; x y x 2 x 1 h S i x x x+h f 1 ( x ) f 2 ( x ) Как улучшить решение? ? Почему не x <= x2 ? ?

5. . Муруй шугамын уртыг олох © К.Ю. Поляков, 2008-2009

6. Муруй шугамын урт Точное решение: Уламжлал олох томъёо хэрэглэх Интеграл авах Ойролцоогоор олох : x y b a y = f ( x ) L x i x i +h f ( x ) L i L 1 L 2 L N

7. Тема 4 . Оптимизация © К.Ю. Поляков, 2008-2009

8. Локальные и глобальные минимумы глобальный минимум Задача : найти глобальный минимум. Реальность : большинство известных алгоритмов находят только локальный минимум вблизи начальной точки алгоритмы поиска глобального минимума в общем случае неизвестны Что делать : для функций одной переменной начальная точка определяется по графику случайный выбор начальной точки запуск алгоритма поиска с нескольких разных точек и выбор наилучшего результата y = f ( x ) локальные минимумы

9. Минимум функции одной переменной Дано : на интервале [a,b] функция непрерывна и имеет единственный минимум. Найти : x * y = f ( x ) Принцип сжатия интервала : Как выбрать c и d наилучшим образом? ?

10. Минимум функции одной переменной Коэффициент сжатия: Самое быстрое сжатие: при должно быть c  d Метод «почти половинного» деления : – малое число нужно искать два значения функции на каждом шаге Постоянное сжатие в обоих случаях : y = f ( x )