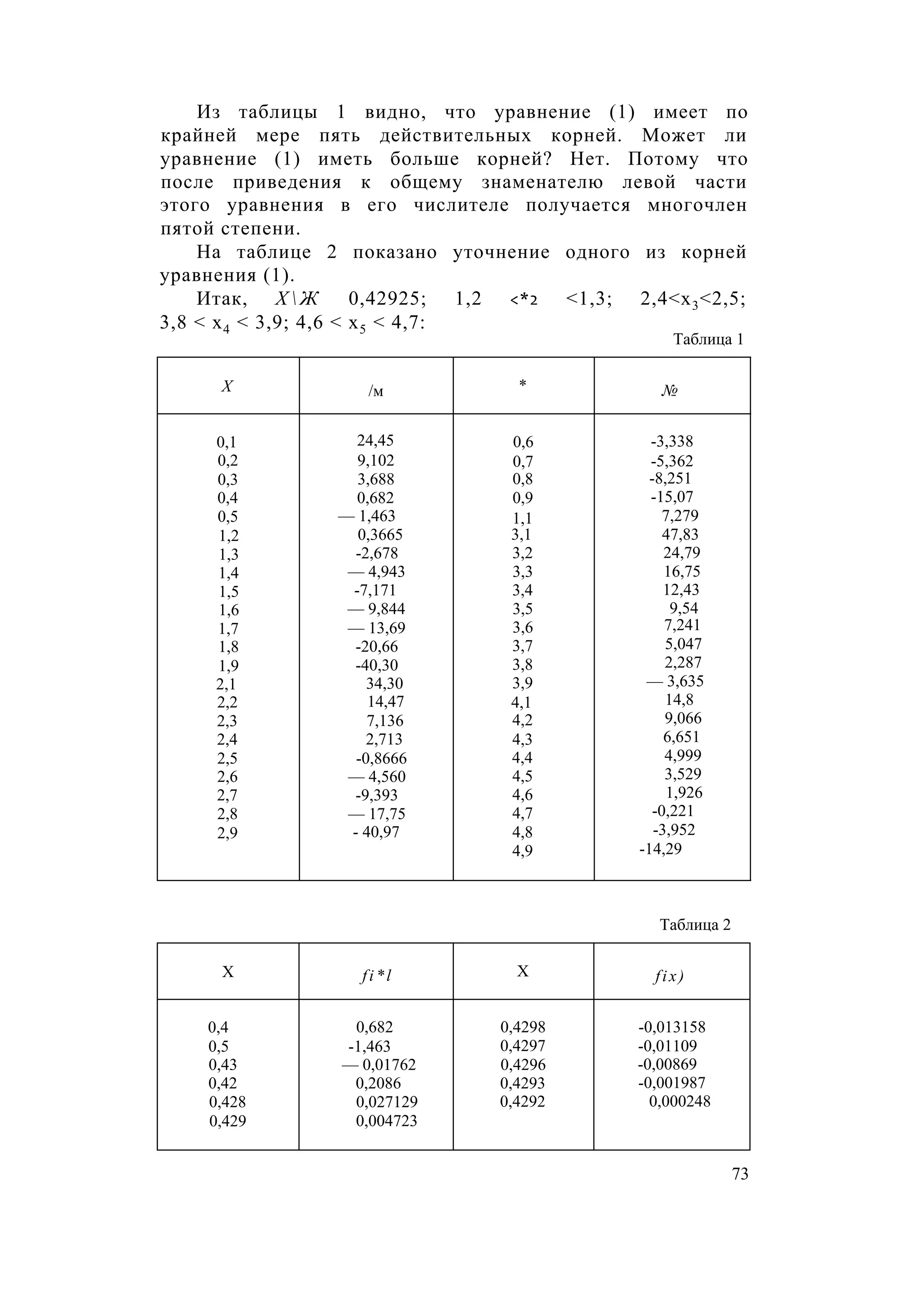
Документ содержит решения систем уравнений и неравенств, включая графический анализ функций и экстремумы. В нескольких задачах рассматриваются различные формулы и подходы к нахождению решений, в том числе с использованием графиков. Большинство решаемых задач приводит к нахождению координат точек пересечения и определению областей, где функции принимают заданные значения.

1. Задание 6. Р А Ц И О Н А Л Ь Н Ы Е У Р А В Н Е Н И Я
И Н Е Р А В Е Н С Т В А
З а д а ч а 1. Решите систему уравнений
( у — х | =2 ( х + у ) ,
IUI + у = 4.
(1)
(2)
Р е ш е н и е . Левая часть уравнения (1) неотрица­
тельна. Поэтому х + у ^ 0, т. е. у ^ —х .
Если | у — х | — 0, т. е. у — х , то х — 0.
Если у > х у то уравнение (1) принимает вид у —
— х = 2 { х + у ) - Отсюда у = — З х .
Если у с х , т о из уравнения (1) получаем х — у =
= 2( х + у ) и у = — *:3.
Таким образом, график f ( x ) уравнения (1) является
объединением лучей О А и О В (рис. 1).
Так как
то осями симметрии графика уравнения (2) являются
оси абсцисс и ординат. Строим сначала ту часть гра­
фика ф(лг) уравнения (2), которая принадлежит первой
координатной четверти:
Получаем отрезок C D . Для построения всего графика
f ( x ) достаточно отобразить отрезок C D относительно
осей координат.
Теперь ясно, что решениями данной системы урав­
нений являются пары чисел ( — 1 ; 3), (3, —1).
З а д а ч а 2. Решите систему уравнений
Р е ш е н и е . Исследуем сначала уравнение (1):
Если х ^ О и у ^ 0, то 2 х = 2 у у т. е. в этом случае
графиком уравнения (1) является биссектриса ОА пер­
вого координатного угла (рис. 2).
Если х <С 0 и у ^ 0, то 0 = 2у , т. е. в этом случае
графиком уравнения (1) будет луч ОС.
Пусть х^О и у ^ 0. Тогда уравнение (1) прини­
мает вид 0=0. Это означает, что все точки третьего
координатного угла являются решениями уравне­
ния (1).
1*1 + у — I — *1 + I у I —I — *1 + I ~ У I —-
= х | + | — у ,
х + у = = 4, х ^ 0, у ^ 0.
{
х + х = у + у у
х — 1 I = х + у .
69

2. Пусть, наконец, х > 0, */<0. Тогда уравнение (1)
преобразуется к виду 2х = 0, т. е. х — 0.
Таким образом, решениями уравнения (1) являются
все точки третьего координатного угла (включая его
стороны) и точки биссектрисы О А первого координат­
ного угла. Исследуем уравнение (2):
Если 1, то х — 1 = х -f- I г/1, т. е. в этом случае
решений уравнение (2) не имеет.
Пусть х < 1 . Получаем 1— х — х - - у или х =
= 0,5(1 - у ) .
Итак, графиком уравнения (2) является объедине­
ние лучей D F и D E .
Находим координаты точки Р, в которой пересе­
каются лучи О А и D F . Отрезок О Р — биссектриса
угла D O F треугольника D O F . Поэтому D P : P F =
-V3 ’ 3 )
Таким образом, решением данной системы уравне­
ний (1) и (2) является каждая точка луча Е Н и точка
З а д а ч а 3. Решите неравенство
а5 - 1,3а2 -2,8а -3,1 >0. (о
Р е ш е н и е . Исследуем на экстремум и монотон-
ность непрерывную функцию
/(а) = а5 — 1,3а2 — 2,8а — 3,1. (1)
Находим:
/'(а) = 5а4 -2,6а -2,8. (2)
Определяем корни уравнения
5а4 — 2,6а — 2,8 = 0 (3)
следующим образом: преобразуем его к виду 5а4 =
— O D : O F = : 2 . Отсюда следует, что Р

3. = 2,6а + 2,8. Строим эскизы графиков непрерывных
функций:
ф(а) = 5а4; и ( а ) = 2,6а + 2,8.
Теперь ясно, что уравнение (3) имеет только два корня
т и п . Уточняем значение корней при помощи микро­
калькулятора:
т « —0,65; п « 1,05.
Поскольку (— 0,65)5 < 0 и — 2,8 • (— 0,65) — 3,1 <0,
то 0. Так как 1,055 < 3,1, то f ( n ) < . 0.
Преобразуем функцию /(а) следующим образом:
/(а) = а(а4 — 2,8) — 1,3а2 — 3,1.
Если а^ — 2, то а4 — 2,8 > 0, а поэтому ясно, что
существует такое значение а, при котором /(а)</(т).
А это означает, что непрерывная функция /(а) на интер­
вале ( — о о , т ) отрицательна и монотонно возрастает
от — оо до f ( m ) .
Очевидно, /(2) > 0, т. е. /(2) > f ( n ) . Следовательно,
непрерывная функция /(а) на промежутке ( п ; +оо)
монотонно возрастает, и ее график пересекает ось
абсцисс в единственной точке а0(1,05 < ао < 2). Поэто­
му решениями данного неравенства (1) являются все
а ^ а0.
Определим ао с точностью до 0,001.
Для упрощения вычислений на микрокалькуляторе
преобразуем f ( a ) так: /(а) = а(а4 — 1,3а — 2,8) — 3,1 =
= а(а(а3 — 1,3) — 2,8) — 3,1.
Составляем при помощи микрокалькулятора табли­
цу значений /(а):
а /О)
1.5
1.6
1,7
1,61
1,62
1.615
1.616
-2,6312507
— 0,4222404
2,5815688
— 0,2379322
0,1
—0,0261103
0,0009
Итак, ао ~ 1,616.
З а д а ч а 4. Решите уравнение
Зл;4 — 2 х 3 + 4*2 — 4 х + 12 = 0. (1)

4. Р е ш е н и е . Преобразуем уравнение (1) к виду:
З х 4 - 2 x : i = — 4 х 2 + 4 х — 1 2 . (2)
Построим графики функций
f ( x ) = З х 4 . — 2 х 3 , ф(х) = — 4 х 2 + 4 х — 12.
Для этого находим:
/'(х) = 12х' — 6 х 2 = 6 х 2 ( 2 х — 1);
с р ' ( х ) = 4 ( — 2 х + 1).
Очевидно, /'*(0) = /'(0,5) = 0; ф'(0,5) = 0. Вычислим:
ДО)— О; /(0,5)= -1; <р(0,5) = -ii; /(- 1) = 5; /(1) =
Графики функций /(х) и ф(х) показаны на рисунке 3.
После исследования функций f ( x ) и ф(х) убеж­
даемся, что уравнение (1) не имеет действительных
корней.
З а д а ч а 5. Решите уравнение
Р е ш е н и е . Функция f ( x ) = §- + -ySy + “—2
-f ' 4,5 - —г-| определена, если х <С 0, 0<
X — о X — 4 X — О
< л< 1, 1 < х < 2 , 2<х<.3, 3 < х < 4 , 4 < х < 5 ,
л >> 5. На каждом из этих интервалов она непрерывна.
Очевидно, f ( x ) > 0, если х ;> 5, и /(х)<С 0, если
х < 0.
Чтобы получить первые представления о поведении
функции f ( x ) на каждом из промежутков (0; 1), (1; 2),
(2; 3), (3; 4), (4; 5), составляем таблицу 1 значений
этой функции при помощи микрокалькулятора.
72

5. Из таблицы 1 видно, что уравнение (1) имеет по
крайней мере пять действительных корней. Может ли
уравнение (1) иметь больше корней? Нет. Потому что
после приведения к общему знаменателю левой части
этого уравнения в его числителе получается многочлен
пятой степени.
На таблице 2 показано уточнение одного из корней
уравнения (1).
Итак, Х Ж 0,42925; 1,2 <*2 <1,3; 2,4<х3<2,5;
3,8 < х4 < 3,9; 4,6 < х5 < 4,7:
Таблица 1
X /м * №
0,1 24,45 0,6 -3,338
0,2 9,102 0,7 -5,362
0,3 3,688 0,8 -8,251
0,4 0,682 0,9 -15,07
0,5 — 1,463 1,1 7,279
1,2 0,3665 3,1 47,83
1,3 -2,678 3,2 24,79
1,4 — 4,943 3,3 16,75
1,5 -7,171 3,4 12,43
1,6 — 9,844 3,5 9,54
1,7 — 13,69 3,6 7,241
1,8 -20,66 3,7 5,047
1,9 -40,30 3,8 2,287
2,1 34,30 3,9 — 3,635
2,2 14,47 4,1 14,8
2,3 7,136 4,2 9,066
2,4 2,713 4,3 6,651
2,5 -0,8666 4,4 4,999
2,6 — 4,560 4,5 3,529
2,7 -9,393 4,6 1,926
2,8 — 17,75 4,7 -0,221
2,9 - 40,97 4,8 -3,952
4,9 -14,29
Таблица 2
X fi*l X fix)
0,4 0,682 0,4298 -0,013158
0,5 -1,463 0,4297 -0,01109
0,43 — 0,01762 0,4296 -0,00869
0,42 0,2086 0,4293 -0,001987
0,428 0,027129 0,4292 0,000248
0,429 0,004723
73

6. Задание 7. РЕШЕНИЕ УРАВНЕНИЙ
И НЕРАВЕНСТВ С ПОМОЩЬЮ ГРАФИКОВ
З а д а ч а 1. Решите неравенство 2 | л: + 11 > х + 4.
Р е ш е н и е . Строим графики функций f ( x ) = 2|х +
+ 1| и ф(х) = л:+4. Аккуратно выполненный чертеж
позволяет найти точное значение координат точек
А и В , в которых пересекаются графики этих функций.
После этого остается только записать ответ: ( — о о ;
— 2) и (2; + оо).
З а д а ч а 2. Назовите множество решений нера­
венства
5 — х < х — 2| + 7 — 2 х . (1)
Р е ш е н и е . Преобразуем данное неравенство к
виду:
U — 2| + |7 — 2 х — |5 — х >0.
Построим график функции
f ( x ) = I* — 2 | + |7-2*| - |5 —*| (рис. 1).
Для упрощения построения надо напомнить сле­
дующее:
1) Выражения х — 2|, | 7 — 2 х [ , |5 — х обра­
щаются в нуль соответственно в точках 2; 3,5; 5.
2) Графиком каждой из функций у — х — 2|, у =
— 17 — 2х|, у = 5 — х является объединение двух
лучей.
3) Поэтому графиком функции f ( x ) является ло­
маная.
4) Для построения этой ломаной находим коорди­
наты ее вершин В , С, D : f ( 2) = 0; /(3,5) = 0; /(5) = 6.
Затем находим значение функции f ( x ) в какой-либо
точке, лежащей левее точки х = 2, и в точке, лежащей
правее точки х = 5 . Например, /(0) = 4 и /(6) = 8.
Осталось только прочитать график функции f ( x ) и
записать о т в е т : ( — оо; 2), (3,5; + оо).
З а д а ч а 3. Решите неравенство х > 3 — 2 х —
— х — 1.
Р е ш е н и е . Преобразуем данное неравенство к
виду:
UI — |3 — 2 х + х+ 1 >0
и строим график функции f ( x ) = х — |3 — 2 х + л: + 1
(рис. 2).
74

7. У
*
В Е
1 ~ос Я 7
Рис. 1 ^ *3,5 5 6 X Рис. 2
Выражения х и |3 — 2х| обращаются в нуль со­
ответственно в точках 0 и 1,5. Графиком функции f ( x )
является ломаная. Для ее построения вычисляем:
/(0) = —2; /(1,5) = 4; /(-1)= -4; /(2) = 4 (точка -1
лежит левее точки 0, а точка 2 расположена правее
точки 1,5)/
Прямая D E , очевидно, параллельна оси абсцисс.
Поэтому график функции /(х), т. е. ломаная A B D E
пересекает ось абсцисс только в одной точке С . Из
подобия прямоугольных треугольников О С В и F C D
следует О С = 0,5. Получаем о т в е т : (0,5; + оо).
З а д а ч а 4. Решите неравенство
Р е ш е н и е . Строим графики функций /(*)= U +
+ 2 | | , ср(х) = х — 11 — 3, f>(x) = 7:ф(х)(рис. 3). Графики
этих функций легко строятся без применения произ­
водной, так как они монотонные на соответствующих
промежутках.
Прямые х = — 2 и х = 4 являются вертикальными
асимптотами графика функции г|)(х).
Для определения абсцисс точек В и С решаем со­
ответственно уравнения
Получаем £(5; 7) и C( — ~[l — 2 ' ^ J l ) . С помощью
рисунка 3 получаем о т в е т : [ — V 7 — 2; —2), (4; 5].
З а д а ч а 5. Решите неравенство х — 2 ^ л [ х .
7
> U + 2I. (1)U— 1| —3
75

8. Р е ш е н и е . Строим графики функций /(х) = х — 2
и ц ( х ) = л / х (рис. 4). После этого становится понятным,
что уравнение х — 2 = л [ х имеет только один положи­
тельный корень Х о > 2, а решением данного неравенства
является промежуток [0; хо], так как данное неравенство
определено только для неотрицательных чисел.
Решив уравнение х — 2 = л [ х путем возведения его
обеих положительных частей в квадрат, получаем
х0 = 4.
Здесь надо заметить следующее:
Во-первых, уравнение (х— 2)2 = х не равносильно
уравнению х — 2=^~[х. Первое из них имеет корни
1 и 4, а второе — только 4. Из рисунка ясно, почему
число 1 является посторонним корнем для уравнения
х — 2 =л[х (точка А есть пересечение графиков функ­
ций / ( х ) = х — 2 И ф|(х) = — ~[х).
Во-вторых, предварительно построенные графики
функций /(х) и ф(х) снимают вопрос о посторонних
корнях соответствующих уравнений и неравенств.
З а д а ч а 6. Назовите множество решений нера­
венства
"^7 + х ^> 5 — х. (1)
Р е ш е н и е . Строим графики непрерывных монотон­
ных функций:
f ( x ) = ^ 7 + х и ф(х) — 5 — х.
Функция /(х) определена на промежутке [ — 7; + оо),
непрерывна и монотонно возрастает. Она изменяется
от 0 до + оо. Функция ф(х) определена для всех дейст­
вительных чисел, она монотонно убывает от + оо до
76

9. — оо. Поэтому уравнение l - - x = 5 — х имеет един­
ственное решение лго- Легко заметить, что Х о = 2. С по­
мощью графика находим о т в е т : (2; + оо).
З а д а ч а 7. Решите неравенство ~ y j x — 1 +
-f- ~ J х + 14 ^ 3.
Р е ш е н и е . Левая часть неравенства определена
на промежутке [1; +оо). Функция f l ( x ) = JJx — 1 не­
прерывная и монотонная (на указанном промежутке
возрастает от 0 до -f-oo). Функция /г(*) = л/х 14
непрерывная и монотонная (на промежутке [1; + оо)
возрастает от ~f5 ' j x o + оо), поэтому непрерывная
функция f ( x ) = f ] ( x ) + f - 2( x ) на полуинтервале [1; + оо)
возрастает от "^15 до + оо*. Так как тосу­
ществует единственная точка х 0 такая, что f ( x о) — 3.
Очевидно, Х о — 2 . О т в е т , х ^ 2 .
З а д а ч а 8. Решите неравенство
.2 .Vf-.+ l— < 1. (1)
1 — 2 “/3 — х
Р е ш е н и е . Выражение 2 ~ у х определено на
полуинтервале [ — 1 ; +оо). Выражение 1 — 2 ~ / з — х
определено и отлично от нуля на промежутках ( — о о ;
2,75) и (2,75; 3], поэтому неравенство (1) определено
на промежутках [ — 1 ; 2,75) и (2,75; 3].
Строим графики функций: f ( x ) = 2л]х + 1 и ф(х) =
= 1 — 2л] 3 — х на промежутках ( — 1 ; 2,75) и (2,75; 3].
Так как на полуинтервале [ — 1 ; 2,75) функция f ( x )
fix) ^ А
неотрицательна, то ^ О на этом промежутке и
полуинтервал [— 1; 2,75) является решением неравен­
ства ( 1 ) .
Функции f ( x ) и ф(х) на полуинтервале (2,75; 3] поло­
жительные и возрастающие: "У 15 С f ( x ) ^ 4; 0 <
f ( х )
< ф(х) ^ 1. Поэтому на промежутке (2,75; 3] >
> 1 > 1.
О т в е т . [ — 1; 2,75).
З а д а ч а 9. Решите уравнение
log3*=i+i^r- 0)
13

10. Р е ш е н и е . Строим графики
функций f ( x ) = log3*, <р(х) =
= 1 + 2 Г ^ Т (Рис- 5)-
На полуинтервале (— оо; 0]
функция f ( x ) не определена,
поэтому на этом промежутке
нет решений уравнения (1).
На интервале (0; 0,5) функ­
ция ф(х) положительна, а фун­
кция f ( x ) отрицательна, поэтому
и здесь нет решений уравне­
ния ( 1 ) .
В точке лг = 0,5 функция ф(х) не определена.
На полуинтервале (0,5; 1] функция /(*)> — 2, а
функция ф(лг)< —2.
На интервале (1; 2) функция f i x ) положительна,
а функция ф(х) отрицательна.
В точке х = 2 функция ф(л:) = 0, а функция f ( x )
положительна.
На полуинтервале (2; 3] функция .ф(лг) < 0,4, а функ­
ция f ( x ) > 0,4.
Наконец, на промежутке (3; + оо) функция ф(х) < 1,
а функция f ( x ) > > 1.
Таким образом, уравнение (1) не имеет решений.
Задание 8. И Р Р А Ц И О Н А Л Ь Н Ы Е У Р А В Н Е Н И Я
И Н Е Р А В Е Н С Т В А
З а д а ч а 1. Решите уравнение ~2х + 5 = 8 —
— у * — г
П е р в о е р е ш е н и е . Преобразуем уравнение к
виду:
•д/2* + 5+ л]х — 1 = 8.
Функция f ( x ) = -j2x + 5 +Ул; — 1 определена для
х ^ , непрерывная и возрастающая. Очевидно,
f ( ) = -[7 <,8. Поэтому существует единственный ко­
рень Х.
Находим значение функции f { x ) при некоторых
значениях х: /(2) = 4, /(5) » 6, /(17) = -[9 + 4 > 8.
После чего ясно, что 5 < * i < 17. Нетрудно заметить,
что /(10) = 8.
78

11. В т о р о е р е ш е н и е . Возводим обе части уравне­
ния в квадрат. Получаем:
2* + 5 = (8 — У* — I)2 или
1 бУ* — 1 = 58 — х.
Возводим в квадрат обе части последнего уравнения
После приведения подобных членов получаем:
х2 - 372* + 3620 = 0.
Корни этого уравнения: х = 10, *2 = 362.
Каждое новое уравнение было следствием преды­
дущего. Поэтому в процессе решения уравнения (1)
могли появиться посторонние корни. Следовательно,
полученные корни нуждаются в проверке:
/(Ю) = 8, /(362) = 46.
Отсюда ясно, что уравнение (1) имеет единствен­
ный корень * = 10.
З а д а ч а 2. Решите уравнение________
~] Зх —1 = 3 —{- л] х — 1. (1)
П е р в о е р е ш е н и е . После возведения обеих ча­
стей уравнения (1) в квадрат получаем:
3* 1 = 9 6 У* — -J- (* — 1)
или
6 -у/х — 1 = 2 х - 7 . (2)
Уравнение (2) после возведения его обеих частей в
квадрат преобразуется к виду: 4*2 — 64* + 85 = 0.
Его корни: *i = 0,5(16 + зУГЁГ) ~ 14,539; *2 = 0,5(16 —
— зУнГ)« 1,4615.
Проверка (при помощи микрокалькулятора) пока­
зывает, что только число *i является его решением.
В т о р о е р е ш е н и е. Найдем наибольшее значение
функции /(*) = 3 +У* — 1 — Уз* + 1 при помощи
производной:
1 2
/'(*)=
5
Решив уравнение /'(*) = 0, получим *— у. Очевидно,
/ 5 5
f l — 1 и /(1)= 1, НО у > *2. Поэтому только число
*1 является решением уравнения ( 1 ) .
79

12. Т р е т ь е р е ш е н и е . После двукратного возведе­
ния обеих частей уравнения (1) в квадрат и приведения
подобных членов получаем уравнение 4х2 — 64* +
+ 85 = 0. Его корни *i и х2.
Проверка найденных корней их подстановкой в
уравнение (1) без помощи микрокалькулятора сопря­
жена с большими трудностями. Поэтому можно при­
менить такой способ проверки:
Область определения уравнения ( 1 ) : * ^ 1. В этом
промежутке первое возведение в квадрат обеих частей
уравнения (1) является равносильным преобразова­
нием. Второе возведение в квадрат применялось к
уравнению 6л[х — 1 = 2х — 7, которому могут удовлет­
ворять только значения х, которые являются реше­
ниями неравенства * ^ 3,5. Устанавливаем, что не­
равенство 0,5(16 + Зд/Тэ^) ^ 3,5 истинно, а неравен­
ство 0,5(16 — зУ19)> 3,5 ЛОЖНО. Поэтому *2 является
посторонним корнем уравнения ( 1 ) .
З а д а ч а 3. Решите уравнение
^[х — 9 = (х — З)3 + 6. (1)
Р е ш е н и е . Стандартные приемы решения этого
уравнения приводят к громоздким преобразованиям
выражений с переменными.
В таких случаях нужно сначала получить гипотезу
о числе решений уравнения. Для этого составим при
помощи микрокалькулятора таблицы непрерывных
функций
f(x ) — л/х — 9 и ф(л:) = (х — З)3 + 6:
X f(x) ф(*) - х ■ /м ф W
0 —2,1 —21 6,5 — 1,4 49
0,5 —2,0 —9,6 7 — 1,3 70
1 —2,0 —2,0 7,5 — 1,1 97
1,5 —2,0 2,6 8 — 1,0 130
2 — 1,9 5,0 8,5 —0,8 170
2,5 — 1,9 5,9 9 0 220
3 — 1,8 6,0 9,5 0,8 280
3,5 — 1,8 6,1 10 1 350
4 — 1,7 7 10,5 1,1 430
4,5 — 1,7 9,4 11 1,3 520
5 — 1,6 14 1 1,5 1,4 620
5,5 — 1,5 22 12 1,4 740
6 . — 1,4 33
80

13. Строим графики функ- у
ций f ( x ) и ф(х) (рис. 1).
Что дает внимательное
изучение таблиц и графи­
ков функций /(х) и ф(х)?
Во-первых, становится
ясным, что решением дан­
ного уравнения является _
число 1.
Во-вторых, на отрезке
[1,5; 9] функция /(х) непо­
ложительная, а функция
ф(х) положительная. Поэтому на этом промежутке
решений уравнение (1) не имеет.
В-третьих, на интервале (9; + оо) функции /(х) и
ф(х) положительны.
Графики этих функций подсказывают, что на интер-
вале (9; + оо) целесообразно заменить выражение
~Jх'—- 9 на д/х — 3. Очевидно, л/х — 3 >> д/х — 9 на
(9; +оо). Правую же часть уравнения (1) уменьшим,
вычтя из него 6.
Итак, попытаемся доказать, что на интервале (9;
+ оо) верно неравенство
.-у/х — 3 < ( х — З)3. (2)
После возведения обеих частей неравенства (2) в куб
получаем:
(х-3)[(х-3)8- 1]>0. (3)
На промежутке (9; + оо) неравенство (3) верно. Значит,
на этом промежутке верно неравенство (1) и, следова­
тельно, неравенство ф(х) ;>/(х).
Таким образом, показано, что на промежутке
[1,5; + оо) уравнение (1) решений не имеет.
На промежутке (1; 3] функция /(х) вогнутая, а функ­
ция ф(х) — выпуклая. Поэтому на этом промежутке
график функции f ( x ) лежит под хордой А С , а график
функции ф(х) лежит над хордой А В (рис. 1). Отсюда
ясно, что и на полуинтервале (1; 3] уравнение (1) реше­
ний не имеет.
На интервале (—оо; 1) график функции f ( x ) нахо­
дится над прямой А В , а график функции ф(х) лежит
под прямой А В . Поэтому и на промежутке (—оо; 1)
уравнение (1) решений не имеет.
81

14. Таким образом, только число 1 является действи­
тельным корнем уравнения ( 1 ) .
З а д а ч а 4. Решите неравенство
~{jx2 + 2х + 10 + х4 ^ 62 — 32х. (1)
Р е ш е н и е . Так как г2 + 2х + 10 = (х + 1 )2 + 9 > 0
при любом значении л:, то данное неравенство опре­
делено при любом действительном значении х. Иссле­
дуем некоторые свойства непрерывной функции
f (х) = ~J{x -f- 1 )2 -f- 9 -j- х 4 -j- 32х— 62. (2)
Если х ^ О , то непрерывная функция f ( x ) — возра­
стающая. Поэтому уравнение f ( x ) = 0 имеет не больше
одного неотрицательного корня х . Но /(0) < 0 и
/(2) > 0, поэтому 0 < х < 2.
Неравенство д/(х + I)2 + 9 > 0 верно при любом
значении х . Поэтому уравнение f ( x ) = 0 не имеет корней
для тех значений х , которые являются решениями не­
равенства х 4 + 3 2 х — 62 ^ 0.
Получаем х 4 + 3 2 х — 62 = х ( х 3 + 32) — 62. Если
х < — 4, то х3 + 32 < — 32 и х ( х 3 + 3 2 ) > 128. Поэтому
при х < — 4 верно неравенство х + 3 2 х — 62 > 0.
Теперь ясно, что отрицательные корни уравнения
/(jc) = 0 могут принадлежать только интервалу ( — 4; 0).
При помощи программируемого микрокалькулятора
составляем таблицу значений функции f ( x ) :
X — 4 -3,5 -3 — 2/5 -2 — 1,5 -1 -0,5 0
f i x ) 68 -22 -75 — 101 -108 -103 -91 -76 -60
На основании этой таблицы можно предположить,
что на отрезке [ — 3,5; 0] уравнение f ( x ) = 0 не имеет
корней. Но как это доказать?
Очевидно,
д/э<7(х+ 1)2 + 9<л/(-3,5+ 1)2 + 9.
Отсюда
1,73<-ЭД* + 1)2 + 9< 1,98. (3)
Выясним, как изменяется функция ф(х) = х4 +
+ 32х —62 на отрезке [ — 3,5; 0]. Находим ф'(х) =
82

15. = 4х3 + 32. Решив уравнение 4г3 + 32 = 0, получаем
х = — 2. Вычисляем:
ф(— 2) = - 110; Ф(0)= -62; ф(-3,5)« -23,9375. (4)
Из условий (3) и (4) ясно, что на всем отрезке
[ — 3,5; 0] функция /(лс)<0.
На отрезке [ — 4; —3,5] непрерывные функции
у = ~](х + 1)2+ 9 и ф(дс) убывающие. И так как
/(— 4) « 68 > 0, а /(— 3,5)« — 22 < 0, то на интервале
( — 4 ; —3,5) существует единственный корень Х 2 урав­
нения f ( x ) = 0.
Для уточнения значений корней х и Х 2 составим
при помощи микрокалькулятора таблицу значений
функции f ( x ) :
л; № X /М
0 -60,22 — 4 68,06
2 20,06 -3 -75,1
1,5 -7,00 -3,5 -21,96
1,6 -2,25 -3,7 9,02
1,7 2,76 -3,65 0,6897
1,65 0,9754 -3,64 -0,92905
1,64 — 0,287 — 3,645 — 0,12166
1,643 — 0,13743 -3,646 0,04029
1,644 — 0,087508
1,645 — 0,037553
1,646 0,012434
Итак, х ж — 3,6455; Х 2~ 1,6455.
Легко заметить, что х + Х « — 2, Х Х 2 ~ — 6.
Решив систему уравнений: х--Х2= ~ — 2, *1X2=— 6,
получим гипотезу:
*1 = — -/7 — 1, х2 = -ф — 1.
Непосредственной подстановкой х и Х 2 в уравнении
f ( x ) = 0 убеждаемся в справедливости этой гипотезы.
З а д а ч а 5. Решите неравенство
2^2х + 8 + -^303 - 5* > 7. (1)
Р е ш е н и е . Исследуем на экстремум и монотонность
непрерывную функцию
/(*)' = 2^2х + 8 + -^303 - 5х. (2)
83

16. Находим:
/'(*)=- °’8
■V(2х + 8)4 -^(303 -5ж)4
Для нахождения критических точек этой функции
решаем уравнение f ' ( x ) = 0:
0,8 1 0,85 1 /оЧ
_ или 7.7.. , Тй =/ОАО ^ (3)т/(2* + 8)4 -д/(303 - 5дс)4 (2^ + 8) (303 - 5л)
Уравнение (3) равносильно совокупности следую­
щих двух уравнений:
= 1 /4ч
2х + 8 303 - 5* ’ w
3@_=_L_. (5)
2*+ 8 5х — 303 v '
Решив линейные уравнения (4) и (5), получаем:
X, = » 38,258301 Iкорень уравне-
1 + 2 л/о,8 - 1
ния ( 4 ) ) .
Х2 = 303-0,4-л^8 + 4_ _ j33,06099 (корень уравне-
2-^08- 1
ния (5)).
Приближенные значения х и х2 получены на микро­
калькуляторе.
Вычисляем на микрокалькуляторе: f ( x ) z z 7 y 3 7
/(*2)« 2,86; /(0)^6,166 </(*,); /(100)« 2,93 </(л)
/(100) > /(*2). /(200)« 2,952 > /(*2); /(1000) «2,983
/(100000)^9,2. /(20000)^6,65.
Строим график непрерывной функции /(*) (рис. 2)
и график функции у = 7 . Эти два графика пересекаются
в точках А , В и С (их абсциссы обозначены соответст­
венно а, b , с ) . Отсюда ясно, что неравенство (1)
верно, если а ^ х ^ Ь и х ^ с . Ясно также, что
0 < а <; х и х < Ь < 100 и 20000 < с < 100000.
Рис. 2
84

17. Более точное значение а , b и с найдем при помощи
микрокалькулятора. Процесс последовательного уточ­
нения значений а, b и с виден из таблицы:
X /м X №
30 7,36 57,13 6,9994
10 6,92 b = 57,125 7,00
11 6,96 30 000 7,2129
а — 12 7,00 25 000 6,9546
50 7,31 26 000 7,0094
60 6,52 25 500 6,988
55 7,14 25 700 6,998
56. 7,08 25 800 7,003
57 7,01 с = 25 750
57,1 7,007
57,11 7,00105
57,12 7,000207
Задание 9. УРАВНЕНИЯ И НЕРАВЕНСТВА
С ПАРАМЕТРАМИ
З а д а ч а 1. Решите неравенство
т х 2 — 2 ( т — ) х + ( т -f 2) < 0 (1)
относительно х [ т — параметр).
Р е ш е н и е . Решаем неравенство (1) относительно
параметра т :
_ 2(х 4-1) / «Л
т < ~ — т г
Если х = 1 , то неравенство (1) ложно.
Для построения графика функции т ( х ) = — 2
{ X 1)
составляем при помощи микрокалькулятора таблицу ее
значений. График подсказывает, что наибольшее зна­
чение функции т ( х ) равно 0,25. Для подтверждения этой
гипотезы достаточно доказать справедливость нера­
венства
-2-^«0,25.
85

18. С помощью графика функции т ( х ) получаем
о т в е т :
если m ^ 0,25, то неравенство (1) решений не
имеет;
если 0 < т < 0,25, то х ^ х ^ Х 2 ( х и Х 2 — корни
уравнения, соответствующего неравенству ( 1 ) ) ;
если т — 0, то х < — 1;
если т < 0, то х < x i , х > Х 2.
З а д а ч а 2. Найдите все значения а, при которых
уравнение
2 lg(jr + 3) = Ig(a*) (1)
имеет единственный корень.
П е р в о е р е ш е н и е . Очевидно, х > — 3, а х > 0,
х ^ О . Из уравнения (1) получаем:
( х + З)2 — а х , а — = (л[х + , если х > 0.
Очевидно,
Отсюда ясно, что для положительных л; наименьшее
значение функции
равно 12. Если — 3 < х <0, то функция (2) убываю­
щая от нуля до — оо.
О т в е т . а = 1 2 и л и а < 0 .
В т о р о е р е ш е н и е . Строим график функции
у = (х--3)2 при х > — 3 . Теперь ясно, что при всех
а С 0 прямая у = а х пересекает график функции
у = { х -+ З)2 только в одной точке. Если а > 0, то прямая
у = а х имеет единственную общую точку с кривой
у = { х + З)2 при х > — 3 только тогда, когда у — а х
является касательной к этой кривой. Отсюда получаем
а = 12.
З а д а ч а 3. Найдите те вещественные значения
параметра а, при которых неравенство
х 2 — [ a *-f- 1)х -f- а 1 0 (1)
верно при всех значениях х , удовлетворяющих условию
х < 1.
86

19. П е р в о е р е ш е н и е . Решаем неравенство (1) отно­
сительно параметра:
х 2 — а х — х + а + 1 > О,
х 2 — х + 1 > а х — а,
а ( х — 1) С х 2 — х + 1. (2)
Так как х < 1, т. е. - 1 1, то х - 1 <0 и из
неравенства (2) получаем (для х — 1 Ф 0!):
Строим график функции а ( х ) = х + —~~f на — 1
< JC < 1.
Для этого вычисляем:
Корнем этого уравнения, принадлежащим полуинтер­
валу [— 1; 1], является только 0. Вычисляем: а(0) = — 1;
а(— 1) = — 1,5; а(1) = — оо.
С помощью графика получаем о т в е т :
— 1 < С а <С + оо.
В т о р о е р е ш е н и е . График функции а ( х ) можно
построить при помощи микрокалькулятора (и без по­
мощи производной!). При помощи микрокалькулятора
легко обнаруживаем, что нужное нам наибольшее
значение функция а ( х ) достигает в точке х = 0. После
этого остается доказать, что
относительно х ( а — параметр) и выполните исследова­
ние свойств их решений.
Р е ш е н и е . Очевидно, х Ф 0. Решаем сначала урав­
нение (1) и неравенства (2) и (3) относительно
параметра а :
«'(*) =1 - -(Г=тг=0-
А это уже совсем простое дело.
З а д а ч а 4. Решите уравнение
х ~ { + а х = 1
и неравенства x ~ l + а х >1
x ~ l + а х < 1
(1)
(2)
(3)
(4)
87

20. Из неравенства (2) получаем:
c l > х - $ если х>>0; (5)
а С х - 2 если х < 0 . (6)
Из неравенства (3) получаем:
1~’ если (7)
(8)
( 1 - 1 ) . Э т а
а > если х < 0 .
Исследуем функцию а =-^-т
X
функция является квадратичной относительно х ~ По­
этому ясно, что она принимает наибольшее значение
в точке х-1=0,5, т. е. при х = 2 .
Обозначим X ] и х2 — корни уравнения ( 1 ) , причем
Х < *2.
Построим график функции а = х ~ х — х ~ 2 . С по­
мощью его можно ответить на следующие во­
просы:
1. Почему график функции а = х ~ 1 — х ~ 2 пересе­
кает ось абсцисс только в одной точке?
2. Почему график этой функции не пересекает ось
ординат?
3. При каких значениях параметра а уравнение (1)
не имеет решений?
О т в е т , а > 0,25.
4. При каких значениях параметра а уравнение (1)
имеет только одно решение?
О т в е т . При а = 0.
5. При каких значениях параметра а уравнение (1)
имеет наибольшее число корней?
О т в е т . 0 < а < 0,25; а < 0.
6. При каком значении а положительный корень
уравнения (1) будет наименьшим?
О т в е т , а — 0,25.
7. Как изменяются корни уравнения ( 1 ) , если
а < 0 и неограниченно уменьшается?
О т в е т . Оба корня уравнения (1) стремятся к нулю.
8. Сравните х и х2, если а < 0.
Решив уравнение (1) относительно х у получаем:

21. Отсюда ясно, что х > х ^ .
9. Существует ли такое значение параметра а, при
КОТОРОМ Х + Х 2 = О?
О т в е т . Не существует.
10. Существует ли такое значение параметра а, при
КОТОРОМ Х > 2 И Х 2 > 2?
О т в е т . Не существует.
11. Существует ли такое значение параметра а, при
котором Х --Х2= 1000?
О т в е т . Не существует.
12. Как изменяется отношение х :х2, если а > 0 и а
стремится к нулю?
О т в е т . Стремится к нулю.
13. При каких значениях параметра а решением
неравенства (2) являются промежутки (0; х ) и
[ Х 2 , + сю)?
О т в е т . 0 < а < 0,25.
14. Какое из неравенств верно: (2) или (3), если
а С 0, x < x i и 0 < х < х 2 ?
О т в е т . Неравенство (2).
15. Точки какого промежутка являются решениями
неравенства (3), если а < 0?
О т в е т . х ' < х < 0, х > Х 2.
16. Существует ли такое значение параметра а, при
котором решением неравенства (3) является проме­
жуток (xi; хг)?
О т в е т . 0 < а < 0,25.
З а д а ч а 5. Рассмотрим ряд свойств уравнений и
неравенств, содержащих переменную под знаком моду-
, ля. Проведем исследование квадратного уравнения и
неравенств ( а — параметр):
Р е ш е н и е . Сначала построим график уравне­
ния ( 1 ) :
если х ^ а , то
а ( х ) = а = — х 2 — 2 х — 2; (4)
если х < а, то
х2 + 4х — 2 | х — а | + 2 — а = 0,
х2 + 4х — 2 | х — а | + 2 — а > 0,
х2 + 4х — 2 | х — а | + 2 — а < 0.
а2(х) = а = у (х2 + 6х + 2). (5)
89

22. Графики функций а ( х )
и а 2{ х ) показаны на ри­
сунке 1.
Числа а = — 3 — д/7
и (3 = — 3 + д/7 — дейст­
вительные корни уравне­
ния J- (.х 2 + 6х + 2) = 0.
О
Если х ^ а, то из не­
равенства (2) находим,
что а > — х2 — 2х — 2.
Если х < а, то из не­
равенства (2) следует,
что а < у(*2 + 6х + 2).
Если х ^ а, то из неравенства (3) следует, что
а < — х2 — 2х — 2.
Если х < а , то из неравенства (3) получаем, что
а ~Ь 6х -|-2).
С помощью графика уравнения (1) можно дать отве­
ты на следующие вопросы:
1. Назовите, при каких значениях параметра а урав­
нение (1) имеет: одно, два, три или четыре решения.
2. Существует ли такое значение параметра а, при
котором уравнение (1) не имеет решений?
О т в е т . Не существует.
3. Назовите наименьшее значение параметра, при
котором уравнение (1) имеет три корня.
~ 7
О т в е т , а = ——.
4. Назовите наибольшее значение параметра а , при
котором уравнение (1) имеет три корня.
О т в е т , а — — 2.
5. Существует ли такое значение параметра а, при
котором один из корней уравнения (1) равен —1,5?
О т в е т . Не существует.
6. Существует ли такое значение параметра а, при
котором наибольший положительный корень уравнения
(1) больше абсолютной величины наибольшего отри­
цательного корня?
О т в е т . Такого значения параметра а не существует,
потому что оси симметрии парабол a i ( x ) = — х —
— 2х — 2 и аг(х) = у(х2 + 6х + 2) сдвинуты от начала
координат влево.
90

23. 7. При каких значениях параметра а сумма всех
корней уравнения (1) отрицательна?
О т в е т . При всех действительных значениях пара­
метра а .
Для удобства в дальнейших рассуждениях обозна­
чим: х , Х 2, х з , х 4 — корни уравнения (1), причем
Х < *2 < Х з < Х 4 .
8. Уравнение (1) имеет корни х и х 4 . Назовите
промежутки, точки которых являются решениями не­
равенства (2).
О т в е т . x < x i , х > х 4 .
9. Уравнение (1) имеет четыре корня: x t Х 2, Х з , х 4 .
Назовите промежутки, точки которых являются реше­
ниями неравенства (3).
О т в е т . x i < x < x 2 , х 3 < х < — 2, — 1 С х С х 4 .
10. Назовите промежуток, на котором верно нера­
венство (3), если один из корней уравнения (1) ра­
вен 1.
О т в е т. х < х <с — 2, — 1 < х < 1.
11. Назовите промежуток, на котором верно нера­
венство (2), если один из корней уравнения (1) равен
нулю.
О т в е т , х <Lxt х> — 1.
12. Существуют ли такие значения параметра а,
при которых неравенство (2) верно для всех действи­
тельных значений х?
О т в е т . Такие значения а существуют. Например,
13. Существуют ли такие значения а, при которых
неравенство (3) верно при всех отрицательных значе­
ниях х?
О т в е т . Не существуют.
14. Существует ли такое значение а, при котором
х 4 — хз = 2000(^2 — *0?
разность х2 — х стремится к нулю, а разность х4 — х3
стремится к 3. Поэтому существует такое значение а,
при котором верно равенство х4 — *з — 2000(^2 — Х ) .
15. Существует ли такое значение а, при котором
х 4 — х 3 = 200(х3 — х2)?
О т в е т . Такое значение а существует.
16. Чему равна сумма корней уравнения ( 1 ) , если
О т в е т . Если а стремится
а = -2?
91

24. О т в е т . О + ( — 2) -f- ( — 4) = — 6.
17. К чему стремится сумма корней уравнения ( 1 ) ,
7 оесли а стремится к — — ?
О т в е т . ( — 3 ) + ( — 3 ) + ( — 2 ) — - 8 .
З а д а ч а 6. Исследуем корни уравнения
х 4 + а ( х — I)4 = 8 ( а — параметр) (I)
и функцию
(2)
Р е ш е н и е. Построим график функции (2) следую­
щим образом. Во-первых, замечаем, что выражение
g ___ ^.4
-т- не определено в точке х = 1. Во-вторых, а ( х ) =
(х — I)4 Г
4Г“ 4 Г- 4j
= 0, если х = — д/8 или х=д/8. Обозначим: — 8 —
= т , д/8 = п .
Составляем при помощи микрокалькулятора табли­
цы значений функций: f ( x ) = 8 — х4, ф(х) = ( х — I ) 4 ,
a ( x ) = f ( x ) : ф(х):
X И*) <р(х) а(х) X f(x) фМ а(х)
0 8,00 1,00 8,00 0 8,00 1,00 8,00
0,2 7,99 0,41 20,0 -0,2 7,99 2,07 3,86
0,4 7,97 0,13 61,3 -0,4 7,97 3,84 2,08
0,6 7,87 0,026 303 -0,6 7,87 6,55 1,20
0,8 7,59 0,0016 4744 -0,8 7,59 10,5 0,72
1,0 7,00 0,00 — -1,0 7,00 16,0 0,44
1,2 5,93 0,0016 3706 — 1,2 5,93 23,4 0,25
1,4 4,16 0,026 160 -1,4 4,16 33,2 0,13
1,6 1,45 0,13 11,2 -1,6 1,45 45,7 0,032
Хо = — Хо =
= 78 0,00 0,24 0 = V® 0,00 53,1 0,00
1,8 -2,50 0,41 -6,09 — 1,8 -2,50 61,5 — 0,041
2,0 — 8,00 1,00 -8,00 — 2,0 -8,00 81,0 -0,10
2,2 -15,4 2,07 -7,44 -2,5 -31,1 150 -0,21
2,4 -25,2 3,84 -6,56 -3,0 -73,0 256 -0,29
2,6 -37,7 6,55 -5,76 -4,0 -248 625 -0,40
2,8 -53,5 10,5 — 5,10 -5,0 -617 1296 -0,48
3,0 -73,0 16,0 -4,56 -10,0 — 9992 14 641 -0,68
3,5 -142 39,1 -3,63 -15,0 -50 617 65 536 -0,77
4,0 -248 81,0 — 3,06 -20,0 -160000 194 481 -0,82
10,0 -9992 6 561 — 1,52 -25,0 -390625 456 976 -0,85
20,0 — 160000 130 321 -1,23
92

25. С помощью таблицы строим графики этих функций
(рис. 2).
Выясним свойства функций f(x), ф(х) и а(х) видны
из таблицы и графиков. Какие из обнаруженных свойств
мы сможем обосновать?
Функция f(x) принимает наибольшее значение в
точке 0, и /(0) = 8. Она изменяется от — оо до 8. Ее
график пересекает ось абсцисс в точках т и п и сим­
метричен относительно оси ординат.
Функция <р(х) неотрицательна; ф( 1) = 0. Она изме­
няется от 0 до + о о . Ее график симметричен относи­
тельно прямой а = 1.
Функция а(х) есть частное функций f(x) и ф(х).
На промежутке [т; 0] функции f(x) и ф(х) положи­
тельны; функция f(x) возрастает от 0 до 8, а функция
ф(х) убывает. Поэтому функция а ( х ) = - ^ щ на этом
промежутке возрастает от 0 до 8.
Таблица и графики функций указывают на то, что
отрицательная функция а(х) на (— о о ; т) больше — 1 и
монотонно возрастает до 0.
Докажем, что если х<Сту то а(х)> —1.
Очевидно,
8 — х4 -X
Поэтому если бу­
дет доказано не­
равенство
то тем самым
докажем, что
а ( х ) > — 1. Но
если х < — 1.
Поэтому верно и
неравенство
а ( х ) > — 1,
если х<С т <С — 1.
93

26. Докажем еще, что если х > п > 1, то а ( х ) > — 8, т. е.
После приведения к общему знаменателю и приведения
подобных членов последнее неравенство принимает вид:
Легко убедиться, что наименьшее значение функции
и ( х ) = 9х2 — 32х + 48 больше 19. А так как х > д/8, т. е.
х >>1,7, то неравенство (4) верно при х > п .
Докажем, наконец, что если х > 2, то а(х) <
< — 1, т. е.
или 2х(2х2 —- Зх + 2) — 9 ;> 0. Очевидно, для х > 2
функция v ( x ) = 2 x 2 — Зх + 2 возрастающая. Ее наи­
меньшее значение (в точке х = 2) равно 4. Поэтому
неравенство 2х(2х2 — Зх + 2) — 9 > 0 при х > 2 верно.
Таблица и график функции а ( х ) позволяют полу­
чить ответы на следующие вопросы:
1. При каких значениях параметра а уравнение (1)
имеет только одно решение?
О т в е т . При а = —8.
2. Сколько корней имеет уравнение ( 1 ) , если а —
= —1?
О т в е т . При а = — 1 уравнение (1) решений не
имеет.
3. При каких значениях параметра а уравнение
(1) имеет два решения?
О т в е т . — 8 <С.а<С— 1 и а >— 1 .
4. Рассмотрите таблицу и назовите те промежутки,
на которых функция <р(х) изменяется быстрее, чем
функция f(x).
5. При каких значениях параметра а оба корня
уравнения (1) положительны?
О т в е т . а < — 1.
6. Пусть х и х2 — корни уравнения (1) и Х2>Х|.
Существуют ли такие значения параметра а, при кото­
рых х2 — х 1 <С 1?
7. Существуют ли такие значения параметра а,
при которых х2 — Xi > 1000?
8. Как изменяются корни х и х2 уравнения ( 1 ) ,
если параметр а уменьшается от —8 до —1?
( x - i y (3)
х(9х2 - 3 2 * + 4 8 ) - 3 2 > 0 . (4)
94

27. 9. Существуют ли такие значения параметра а ,
при которых верны неравенства: Х Х 2 <С 0 и Х Х 2 > — 1 ?
10. Как изменяется произведение Х Х 2 , если а уве­
личивается от 0 до + о о ?
11. Существует ли такое значение параметра а,
при котором уравнение (1) имеет три корня?
12. К чему стремится сумма х '+*2, если а неогра­
ниченно возрастает?
13. Верно ли, что х 4 + a ( x — I)4 > 8, если — 1<
< а < 1 ?
У к а з а н и е . При обосновании ответа используйте
таблицу и рисунок.
14. Почему не существует такого значения а, при
котором один из корней уравнения (1) равен 1?
15. Верно ли, что х 4 - + а ( х — I)4 > 8, если х < х <
< х2?
16. При каких а верно неравенство
х 4 + а ( х — I)4 > 8
для всех х, принадлежащих полуинтервалу [3; 4)?
О т в е т , а > а ( 4 ) .
З а д а ч а 7. Дано уравнение
г3 + (2 — а ) х — а — 3 = 0. П
Постройте график этого уравнения и исследуйте его
корни ( а — параметр).
Р е ш е н и е . Преобразуем уравнение (1) следующим
образом:
х^ -{- 2,х — 3 (х — 1) • (х2 -j- х -f- 3)
а X + 1 х -f-1
= (*— l)(x + —ру- ) = *(*— l) + i^il =
= x { x - 1) + 3(1 +T-f^r) =
^ ^ _ l ) + 3 _ _ 6 _ . ( 2 )
Составляем при помощи микрокалькулятора табли-
g
цы функций: f ( x ) = х { х — 1) + 3; ф(х) =------------------ ; а ( х ) =
= f ( x ) + <р(4
95

28. Таблица 1
X т фМ а(х) X ■т ф(х) . Ф)
-1,0 5,0 — 1,0 5,0
-1,2 5,6 50 55,6 -0,8 4,4 -30,0 -25,6
— 1,4 6,4 15 21,4 -0,6 4,0 -15,0 -11,0
— 1,6 7,2 10 17,2 -0,4 3,6 — 10,0 -6,4
-1,8 8,0 7,5 15,5 -0,2 3,2 -7,5 -4,3
-2,0 9,0 6,0 15,0 0,0 3,0 -6,0 -3,0
-2,2 10,0 5,0 15,0 0,2 2,8 -5,0 -2,2
-2,4 11,2 4,3 15,5 0,4 2,7 -4,3 -1,6
-2,6 12,4 3,8 16,2 0,5 2,5 — 4,0 -1,5
-2,8 13,7 3,3 17,0 0,8 2,9 -3,3 -1,4
-3,0 15,0 3,0 18,0 1,0 3,0 -3,0 0,0
-3,2 16,4 2,8 19,2 1,2 3,2 -2,7 0,5
-3,4 18,0 2,5 20,5 1,4 3,6 -2,5 М
-3,6 19,6 2,3 21,9 1,6 ' 4,0 -2,3 1,7
-3,8 21,2 2,1 23,3 1,8 4,4 -2,1 2,3
— 4,0 23,0 2,0 25,0 2,0 5,0 -2,0 3,0
Строим графики функций /(*), ср(х) и а ( х ) (рис. 3).
В таблице 2 уточнено наименьшее значение функции
а ( х ) на отрезке [ — 3; —2]: а(хо) ~ 14,961944; х 0 ~
& -2,0785:
Таблица 2
а{х) X а(х)
— 2,0 15,0 — 2,06 14,96398
-2,2 15,04 -2,08 14,961955
-2,15 14,99 -2,075 14,96202
-2,05 14,967 -2,085 14,962179
-2,03 14,976 -2,081 14,961977
-2,07 14,9624 — 2,079 14,961945
Используя таблицы 1, 2 и рисунок 3, ответьте на
следующие вопросы:
1. Назовите наименьшее значение функции f ( x ) .
2. Чему равно наибольшее значение функции f ( x )
на отрезке [0; 2].
3. Назовите наименьшее значение функции f ( x ) на
полуинтервале ( — 1 ; 0].
4. Назовите наименьшее значение функции f ( x ) на
интервале (— 1; 1).
5. На каком промежутке функция f ( x ) убывает?
96

29. 6. На каком проме­
жутке функция f ( x ) воз­
растает?
7. Докажите, что фун­
кция ф(х) на интервале
( — 4; —1) возрастает.
8. Назовите прибли­
женное значение х, при
котором верно равенство
f { x ) == ф(х).
9. Почему уравнение
f ( x ) = ф(х) имеет только
одно решение?
10. Верно ли, что фун­
кция ф(х) возрастающая?
11. Чему равно наи­
большее значение функ­
ции ф(х) на полуинтервале
( - 1; 2] ?
12. В скольких точках
график функции ф(х) пе­
ресекает ось ординат?
13. Почему график
функции ф(х) не пересека­
ет оси абсцисс?
14. Докажите неравенство а ( х 14, если — 2 , 2 ^
< л < —2,0.
Р е ш е н и е . Непрерывная функция f ( x ) на отрезке
[ — 2,2; —2,0] убывает от 10 до 9 (см. таблицу 1).
Непрерывная функция ф(х) на этом отрезке возрастает
от 5 до 6. Но а ( х ) = f ( x ) + ф(^). Поэтому на отрезке
[ — 2 , 2 ; —2,0] функция а ( х ) не может быть меньше
14(9 + 5=14).
15. Докажите, что уравнение /(х) = ф(х) не имеет
положительных корней.
16. Имеет ли корни уравнение а ( х ) = ф(х)?
Р е ш е н и е . Не имеет, потому что а ( х ) = ф(х) + f ( x )
и /(*) > 0.
17. Почему функция а ( х ) возрастает на промежутке
[0; 0,5]?
Р е ш е н и е . На этом промежутке f ( x ) убывает от
3 до 2,5, а функция ф(х) возрастает от —6 до —4.
Поэтому а ( х ) возрастает.
18. При каких значениях параметра а уравнение
х 3 + (2 — а ) х — а — 3 = 0 не имеет корней?
4 А. Б. Василевский 9 7

30. 19. Назовите несколько значений параметра а, при
которых уравнение х 3 + (2 — а ) х — а — 3 = 0 имеет:
только один корень; три корня; два отрицательных
корня; один отрицательный корень; только положи­
тельный корень.
20. Существует ли такое значение параметра а, при
котором сумма всех трех корней уравнения х3 + (2 —
— а ) х — а — 3 = 0 положительна?
21. Существует ли такое значение а, при котором
корень уравнения х3 + (2 — а ) х — а — 3 = 0 равен — 1 ?
22. Как изменяются корни уравнения х3 + (2 —
— а ) х — а — 3 = 0, если параметр а увеличивается от
-6 до 20?
23. Существует ли такое значение параметра а, при
котором произведение трех действительных корней
уравнения х3 + (2 — а ) х — а — 3 = 0 больше 1000?
Задание 10. ИССЛЕДОВАНИЕ УРАВНЕНИЙ
И НЕРАВЕНСТВ
З а д а ч а 1. Сколько решений имеет уравнение
~[х + х3 = 5?
Р е ш е н и е . Функция f ( x ) — ~[х + х 3 определена для
х ^ 0, непрерывная, монотонная, неотрицательная,
изменяется от 0 до + оо. Поэтому данное уравнение
имеет только одно решение Х. Очевидно, 1 <xi<2.
З а д а ч а 2. Существует ли корень Х о уравнения
sin 2 х + 5 sin х + 5 cos х + 1 = 0, если 0 ^ Х о ^ 0,25л?
Р е ш е н и е . Не существует. Если 0 ^ ^ 0,25я, то
все слагаемые левой части этого уравнения неотрица­
тельны.
З а д а ч а 3. Уравнение
sin 2 х + 5 sin х + 5 cos х + 1 = 0 (1)
преобразовали следующим образом:
2 sin х cos х + 5 sin х + 5 cos x + 1 = 0;
cos x ( 2 sin x + 5) = — 1 — 5 sin x ,
C 0 S X = -L-J^. ( 2 )2 sin x + 5 4 '
c o s x = - —1!A__2,5. (3)
2 sin x + 5
Докажите, что уравнения (1), (2), (3) равносильны.
98

31. Как изменяются cos х , 2 s i n x + 5, ^"+5 и -
— 2,5,если х увеличивается от 0,5л до л? Докажите,
что на отрезке [0,5л; л] уравнение (3) имеет един­
ственный корень.
З а д а ч а 4. Докажите, что уравнение
3 tg 2л: — 4 tg Зл: = tg2 З х tg 2 х (1)
Уе имеет корней, принадлежащих интервалу ^0;
Р е ш е н и е . Если 0 < С х < у , то функции tg 2 х и
i g 3 x положительные и возрастающие. Отсюда ясно,
что на ^0; левая часть уравнения (1) отрицатель­
на, а правая положительна.
З а д а ч а 5. Уравнение
3 tg 2л: — 4tg3* = tg23xtg2x (1)
преобразовали следующим образом:
tg 2 х = —, (2)
ё 3 — tg2 Злг w
tg 2х — 3 — З х _ — Зл_ . (3)
Какие два из уравнений ( 1 ) , (2), (3) равносильны
между собой?
З а д а ч а 6. Сколько решений имеет уравнение
arcsin 2 х + arcsin х — (1)
Р е ш е н и е . Функция f ( x ) = arcsin 2 х определена на
отрезке [ — 0,5; 0,5], а функция ф(х) = arcsin х опреде­
лена на отрезке [ — 1 ; 1]. Поэтому левая часть уравне­
ния (1) определена на отрезке [ — 0,5; 0,5]. Монотон­
ная и непрерывная функция у = arcsin 2 х + arcsin х
изменяется на отрезке [ — 0,5; 0,5] от ^—5. — J L ) до
(я . я 2 2 т т я _ 2 т - г
Т ' Т )’ т' е‘ от ~ ~ J n до Т71' Т <TJt* Поэтому
уравнение (1) имеет единственное решение.
З а д а ч а 7. Уравнение
1 + cos 2х cos Зх = 0,5 sin2 Зх (1)
99

32. преобразовали следущим образом:
0,5 sin2 3jc — 1
cos 2х — — --------------- *
cos Зле
С C/f
cos 2х
_ 0,5(1 — cos2 Зх) — 1 .
cos Зх
1
cos2x = +cos Зх^. (2)
Докажите, что уравнения (1) и (2) равносильны. До­
кажите, что двойное неравенство
— 2 < —!-т—- cos Зх < 2
cos Зх
не имеет решений. Докажите, что уравнение (2) равно­
сильно совокупности систем уравнений:
г cos Зх = 1, rcos Зх == — 1,
{cos 2х — — 1, (cos 2х — 1.
З а д а ч а 8. Уравнение
sin х + cos х = -д/2 + sin4 4х (1)
преобразовали к виду:
"/2 + sin4 4х — sin х — cos х == 0.
В таблице выписаны некоторые значения функции
/(х) = ~д/2 + sin4 4х — sin х — cos х, полученные при по­
мощи микрокалькулятора:
х° /М *° f ( x )
0 0,414 195 3,201
15 0,752 210 2,343
30 0,611 225 2,828
45 0,000 240 3,343
60 0,611 255 3,201
75 0,752 270 2,414
90 0,414 285 2,684
105 1,270 300 2,343
120 1,611 315 1,977
135 1,414 330 1,541
150 2,340 345 1,270
165 2,684 360 0,414
180 2,414
100

33. Рассмотрев таблицу, можно предположить, что на
отрезке [0; 2л] уравнение имеет только один корень
X i = ~ , а в остальных точках этого отрезка функция
f ( x ) положительная.
Наименьшее значение правой части уравнения (1)
равно "У2 ^в точках х = ~ и * ~ у Выясним, чему
равно наибольшее значение левой части этого данного
уравнения. Для этого исследуем функцию ф(х) =
= sin х + cos х. Находим ф'(х) = cos х —- sin х. Оче­
видно, ф'(х) = 0, если х — Вычисляем ф ^ у ^ = 2.
Итак, уравнение (1) на отрезке [0; 2л] имеет един­
ственный корень х = ~ .
З а д а ч а 9. Уравнение
4 sin4 З х — 3 cos х + 5 = 0 (1)
преобразовали к виду:
4 sin4 Зл: 4- 5 /г>ч
COS X =--------T~L—. (2)
О
В каких пределах изменяются функции /(х) = cos х
/ ч 4 sin4 Зх 4- 5
И <р{*) =------------- з——?
Сколько решений имеет уравнение ( 1 ) ?
О т в е т . Уравнение (1) не имеет действительных
корней.
З а д а ч а 10. Неравенство
^/2х + 5 ^ 8 — д/х — 1 (1)
преобразовали к виду:
д/2х + 5 + д/х —~ 1 ^ 8. (2)
Докажите, что функция /(х) == д/2х + 5 +д/лс ~ 1
возрастающая. Почему уравнение д/2х + 5 + д/х — 1 ==
— 8 имеет единственный корень х = 10? Назовите все
решения неравенства (2).
О т в е т. х ^ 10.
З а д а ч а 11. Докажите, что уравнение д/х + 3-f-
— 2 = 7 имеет единственный корень Х.
101

34. Р е ш е н и е . Функция f ( x ) = л / х + 3 -f л/Зл: — 2
. 2
определена для лг ^ —, возрастающая, непрерывная,
/(■|-) = < 7. Легко заметить, что лч = 6.
З а д а ч а 12. Уравнение
-/22 —л; —-/l0 —* = 2 (1)
преобразовали следующим образом:
(-/22 — х — -/l0 — х ) (~/22 — х + ~/l0 — л:) 2-
~у/22 — л: + “д/lO — х
* (22 — х) — (10 — х) _д.
^22 - л: + -т/Ю - л:
V — 6 . ----------= 1 - ( 2 )
”у22 — л; + "у 10 — х
Для каких значений х определена функция f ( x ) =
= “/ 22 — лс + ^Ю — х ?
Докажите, что функции f ( x ) и ф(лг)==__ монотонные.
1Х)
В каких пределах изменяются функции f ( x ) и ф(л:)?
Сколько решений имеют уравнения (2) и (1)? Назо­
вите целое число, которое является решением уравне­
ний (2) и (1).
З а д а ч а 13. Найдите наименьшее значение функ­
ции
t|)(jc) = -/l5 — 12 cosx + "^7 — 4д/з sin х (1)
на отрезке [0; 0,5я].
Р е ш е н и е . Т а к к а к | c o s x | ^ l и | s i n x | < l , то
функция я|)(лг) определена на всем отрезке [0; 0,5л1.
Для поиска свойств функций f ( x ) = ^ J 15 — 12 cos х ,
ф(х)= у7 — sin лг, ■ф(х) = f ( x ) -j- ф(лг) составляем
при помощи микрокалькулятора таблицу их значений:
102

35. * ° /<*) <рМ <р(х)
0 1,7320508 2,6457513 4,3778021
5 1,7451827 2,5290645 4,2742472
10 1,7839021 2,4076816 4,1915837
15 1,8463179 2,2818523 4,1281702
20 1,9296859 2,1518401 4,0815260
25 2,0308387 2,0179237 4,0487624
30 2,1465542 1,8803984 4,0269526
35 2,2738018 1,7395827 4,0133843
40 2,4098684 1,5958185 4,0056869
45 2,5523945 1,4494896 4,0018841
50 2,6993608 1,3010333 4,0003941
55 2,8490493 1,1509769 4,0000262
60 3,0000020 0,9999989 4,0000001
65 3,1509650 0,84906731 4,0000323
70 3,3008723 0,69972737 4,Q003597
75 3,4487928 0,55485998 4,0036527
80 3,5939145 0,42077535 4,0146899
85 3,7355228 0,31330512 4,0488279
90 3,8729833 0,26794924 4,1409325
На основании таблицы можно высказать предполо-
жение, что на отрезке [0; 0,5я] функция i|?(x)>4, при­
чем ) — 4-
Итак, попытаемся доказать, что
-л/15 — 12 cos х+ "^7 — 4^3 sin 4. (2)
Пусть д/7 — 4-/з sin x = t .
7 /2 I (7 /22
Отсюда sinx = —, cosx = - / l ---------------------- ^— и нера-
4 д/3 v
венство (2) принимает вид:
V l 5 - V 3 - V 4 8 - ( 7 - / 2 ) 2 > 4 - ^ . (3)
Обе части неравенства (3) неотрицательны, поэтому
после возведения его обеих частей в квадрат получаем
равносильное неравенство
15 — д/3 • л/48 — (7 — /2)2 >(4 - О2
ИЛИ
-/3'У48-(7-/2)2<8^- 1 -/2.
Отсюда /4 — 4/3 + 6/2 — 4/ + 1 ^ 0.
103

36. Применив теорему Безу, получаем ( t — 1) • ( t 3 —
— 31 + 3/ — 1 ) ^ 0 или ( t — 1 )4 ^ 0.
Таким образом доказано, что наименьшее значение
функции 'ф(х) равно 4.
З а д а ч а 14. Выясните, каким необходимым и до­
статочным условиям должны удовлетворять числа
а, b , с, для того чтобы уравнение х3 + а х 2 + Ь х + с =
= 0(1) имело три действительных корня, образующих
арифметическую прогрессию.
Р е ш е н и е . Обозначим х = р + t . После этого дан­
ное уравнение (1) преобразуется к виду:
+ (а + 3 p ) t 2 + (3 р2 + 2 а р + b ) t +
+ { р 3 + а р 2 + Ь р + с ) = 0. (2)
Если р = — а : 3,
принимает вид
т. е. а + 3р = 0, то уравнение (2)
t
I / и я3 j. I / 2а3 ab ,
+ (*- —)' + (^7------------------3- + С) =
ИЛИ
t3 =
а/?
“3~
2а3
"27“ о-
(3)
(4)
Построим графики функций f ( t ) = t 3 и ф(/) =
= (4 “ (рис* ТепеРь ясно>
что прямая <р(/) пересекает кубическую параболу f ( t )
в точках А и В , симметричных относительно начала
координат, если
a b
“з”
2 а
"27
а
Т (5)
Если — b ^ 0 и — с 0 и прямая ф(/)
функции /(/),
Рис. 1
ab 2 а3
“3 27
пересекает график функции ДГ), то
корни уравнения (4) не симметричны
относительно начала координат.
Итак, необходимым и достаточным
условиями, при которых корни данного
кубического уравнения вещественны
и образуют арифметическую прогрес­
сию, служат соотношения (5).
З а д а ч а 15. Решите уравнение
—s— = _L + ii. (и
х ± 1 2 [ )
104

37. Р е ш е н и е . Положительная функция Р ( х ) = —-
V1 — х2
определена на ( — 1 ; 0) и (0; 1). Положительную функ-
ч 1 , 85 / , 12
цию /г(х) = у + у2 рассматриваем на # — 1; — gg) и
(0; 1). Для получения гипотезы о числе корней уравне­
ния составляем таблицы функций Р ( х ) и F ( x ) :
X Р(х) F{x) ■X Р(х) F(x)
-1 оо 6,08 0 5 ОО
-0,9 11,4 5,97 0,1 5,02 17,1
-0,8 8,33 5,83 0,2 5,10 12,1
-0,7 7 5,65 0,3 5,24 10,4
-0,6 6,25 5,41 0,4 5,46 9,58
-0,5 5,77 5,08 0,5 5,77 9,08
-0,4 5,46 4,58 0,6 6,25 8,75
-0,3 5,24 3,75 0,7 7 8,51
-0,2 5,10 2,08 0,8
4 •т12
85
5,05 0 1 оо 8,08
(12
— 1; —J убывают.
Методом «ступенек» легко доказывается, что на этом
промежутке уравнение (1) корней не имеет. На (0; 1)
непрерывная функция Р ( х ) возрастает, функция F ( x )
убывает. Число 0,8 является единственным корнем
уравнения ( 1 ) .
З а д а ч а 16. Решите уравнение
lg(*2 + 9) — 3 • 2Л' + 5 == 0. (1)
Р е ш е н и е . Отрицательных корней уравнение не
имеет, потому что на (— оо; 0) функция Р { х ) = lg(*2 +
+ 9) + 5 убывает, функция К ( х ) = 3 • 2х возрастает и
Р(0)>/С(0).. Для получения гипотезы о числе корней
данного уравнения составляем таблицы функций Р ( х )
и К { х ) :
105

38. X Р(х) К(х) X Р(х) К{х)
0 5,954 3 1,6 6,062 9,09
0,2 5,956 3,45 1,8 6,087 10,4
0,4 5,961 3,95 2 6,113 12
0,6 5,971 4,55 2,2 6,141 13,8
0,8 5,984 5,22 2,4 6,169 15,8
1 6 6 2,6 6,197 18,2
1,2 6,018 6,89 2,8 6,226 20,9
1,4 6,039 7,92 3 5,255 24
Теперь можно сделать предположение, что если
х > 2 , то lg(x2 + 9)<2* (это неравенство легко дока­
зывается при помощи производной). После этого ста­
новится ясным, что все корни данного уравнения при­
надлежат отрезку [0; 2]. Число 1 является корнем
уравнения.
Из таблицы ясно, что отрезкам [0; 0,8] и [1,2; 2] не
могут принадлежать корни уравнения (1).
Для доказательства того, что 1 является единствен­
ным корнем уравнения (1), составляем таблицы функ­
ций Р ' ( х ) и к ' ( х ) :
Р'(х) К'(х) Р'(х) К'(х)
0,8 0,072 3,6 1,1 0,093 4,4
0,9 0,079 3,8 1,2 0,099 4,7
1 0,080 4,1
Теперь ясно, что на интервале (0,8; 1,2) функция
у = р ( х ) — К ( х ) убывает.
З а д а ч а 17. Вычислите наименьший корень Х о урав­
нения
л;2 — ->Jlg х + 100 = 0 (1)
(с относительной погрешностью не более 10“390 %).
Р е ш е н и е . Уравнение (1) определено на [10” 00;
+ оо). Пусть Р ( х ) = х 2 — ^ f g ^ c + 100. Очевидно,
Р(Ю-100)> 0; Р( 1 ) < 0 ; />(0,1) <0.
Заменим уравнение (1) равносильным ему уравне­
нием л:4 = lg л; + 100. Обозначим: М ( х ) = х F ( x ) =
= l g x + 1 0 0 . Находим М ' ( х ) = 4x3
t F ' ( x ) = 1 : ( х In 10).
106

39. Если 10“100 < х < 0,1, то М ' ( х ) <С F ' ( x ) . Отсюда
следует, что наименьший корень данного уравнения
принадлежит интервалу (10" ; 10“1). Этому интервалу
другие корни уравнения (1) не принадлежат.
Заменим уравнение (1) равносильным ему урав­
нением
| х = ~Jlgx+ 100. (2)
Если * = 10-100+10~396, то "/lgx + 100 = 10“".
Так как 10~100_^ 10-396 <С 10 ", то наименьший корень
уравнения (1) принадлежит интервалу (10“100;
lO-ioo+io-396). Но
Ю - 1 0 0 + 1 0 — _1 0 - ю о 96
10~юо
Теперь остается доказать, что Ю10 3% < 10“392. При
106/—
помощи микрокалькулятора получаем у Ю< 1,000003.
Так как л[+а < 1 + — (если 0 < а < 1), то
jq390 /-6 --- 6^ г—_______
Ю10'396 = д/ у 10 < 1 Vl.000003 < 1 + 10~395.
Ответ. 10_ l 0 0 <jc0 < io_100+10"39e.
З а д а ч а 18. Найдите корни уравнения F ( x ) =
= 2 2 х — 5 • 3 х + 29 = 0 (с точностью до 0,01).
Р е ш е н и е . Данное уравнение равносильно урав­
нениям:
4* + 29 = 5 • 3х, 1п(4х + 29) = 1п5 + *1пЗ.
Пусть Р ( х ) = 1п(4* + 29) — х In 3 — In 5.
Решив уравнение Р ' ( х ) = 0, получаем 4 х = 29 In 3:
:ln-i. Отсюда *1п 4 = In-Щ"^- и х0« 3,395578 (ко-
рень х о уравнения Р ( х ) = 0 получен на микрокальку­
ляторе).
Находим:
F ( x о)да - 68,73277; F { 0) = 29; F ( 6) = 480.
Теперь ясно, что уравнение F(x) = 0 имеет два корня.
Причем, Х =2, х о < х 2 < 6. После уточнения получаем
Х 2 ~ 5,55(4= 0,01).
107