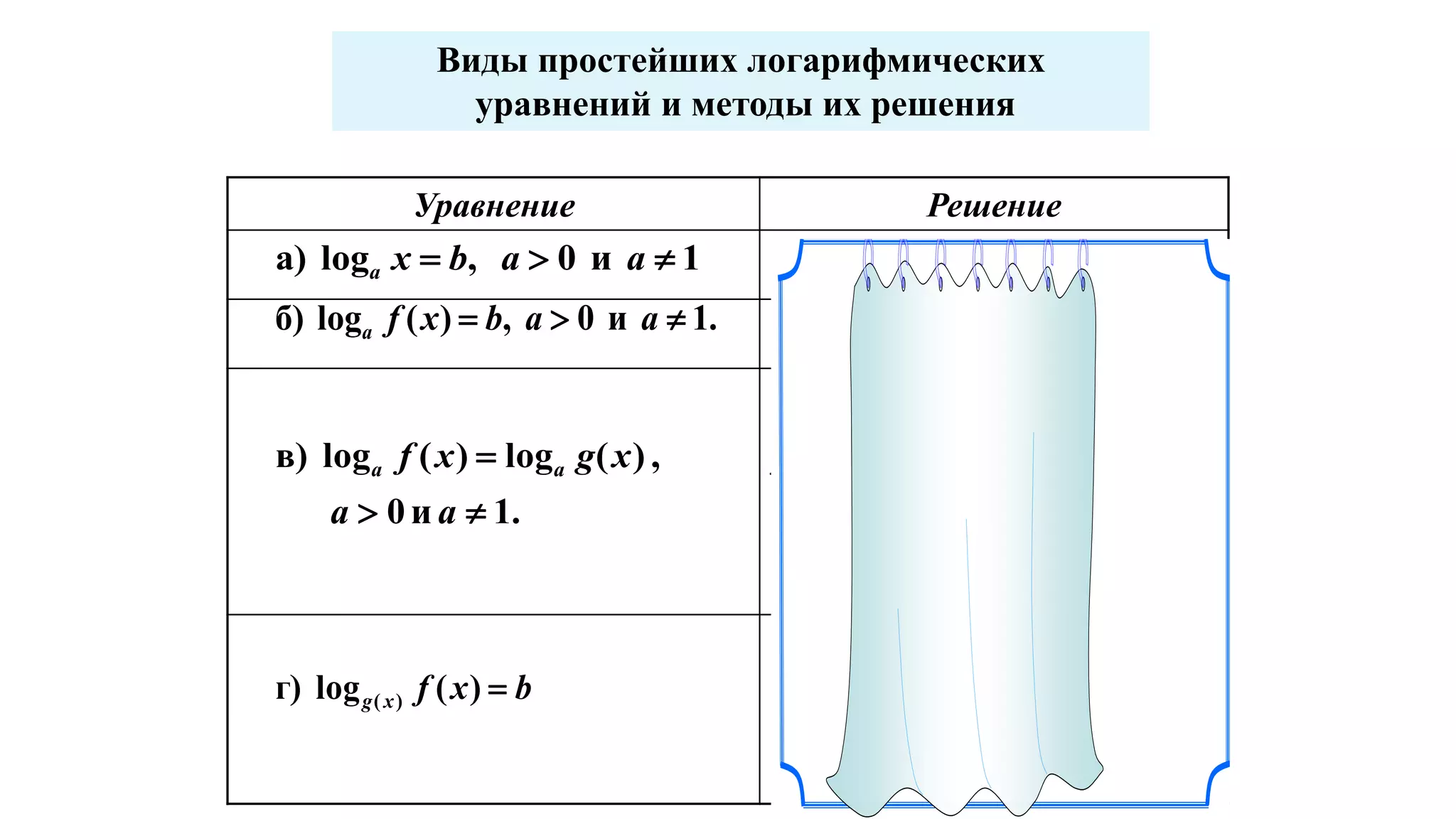
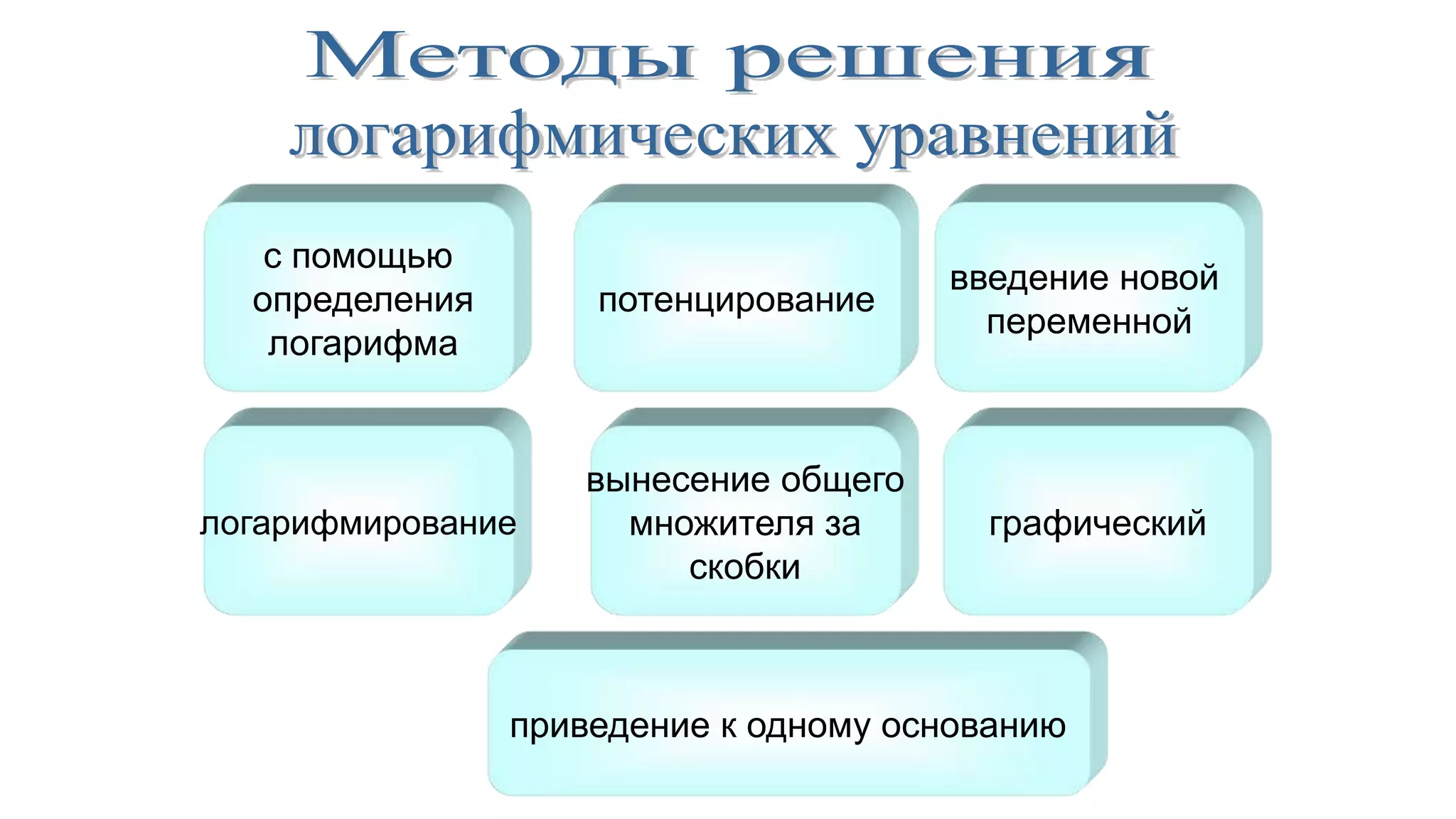
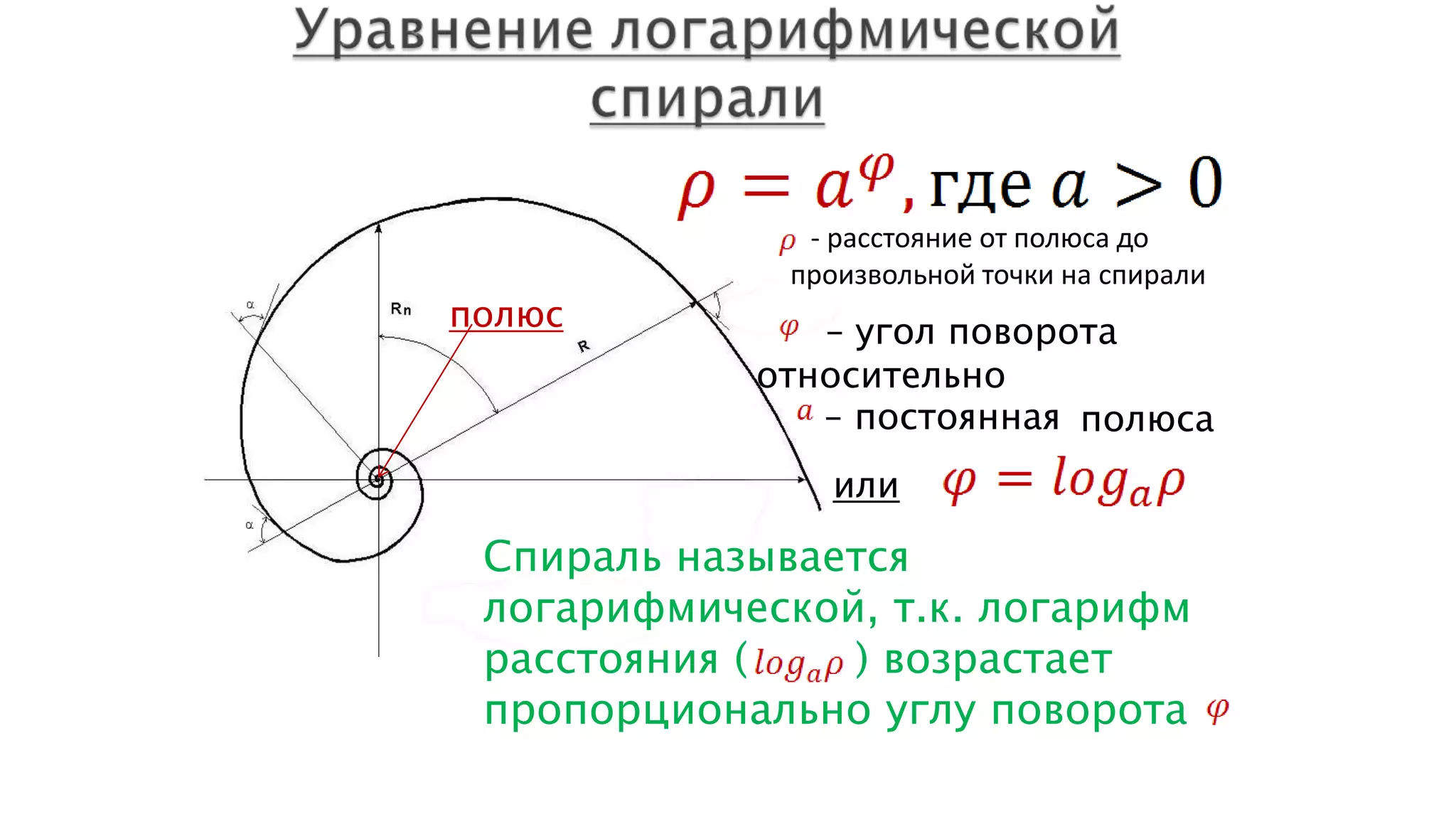
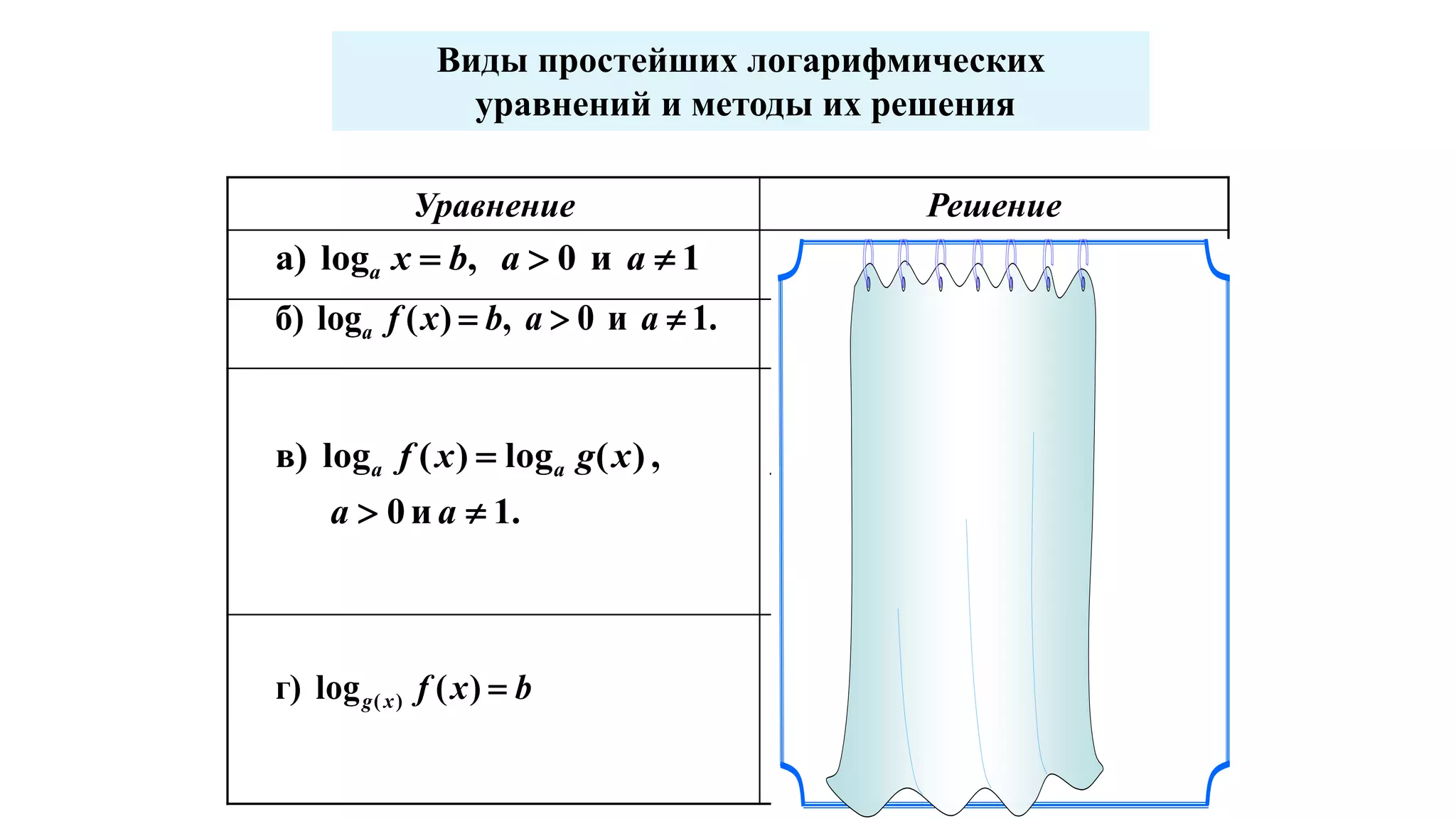
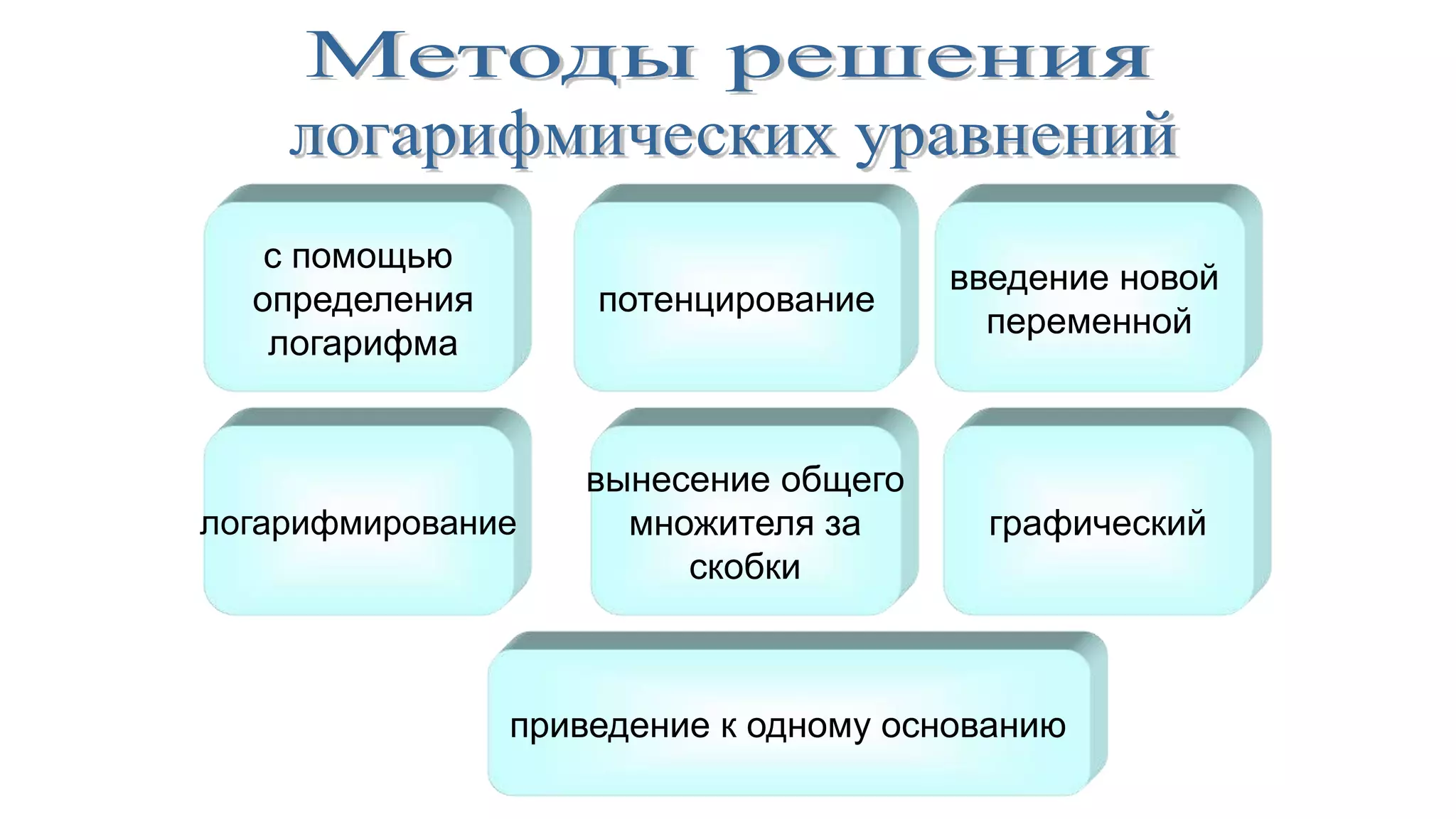
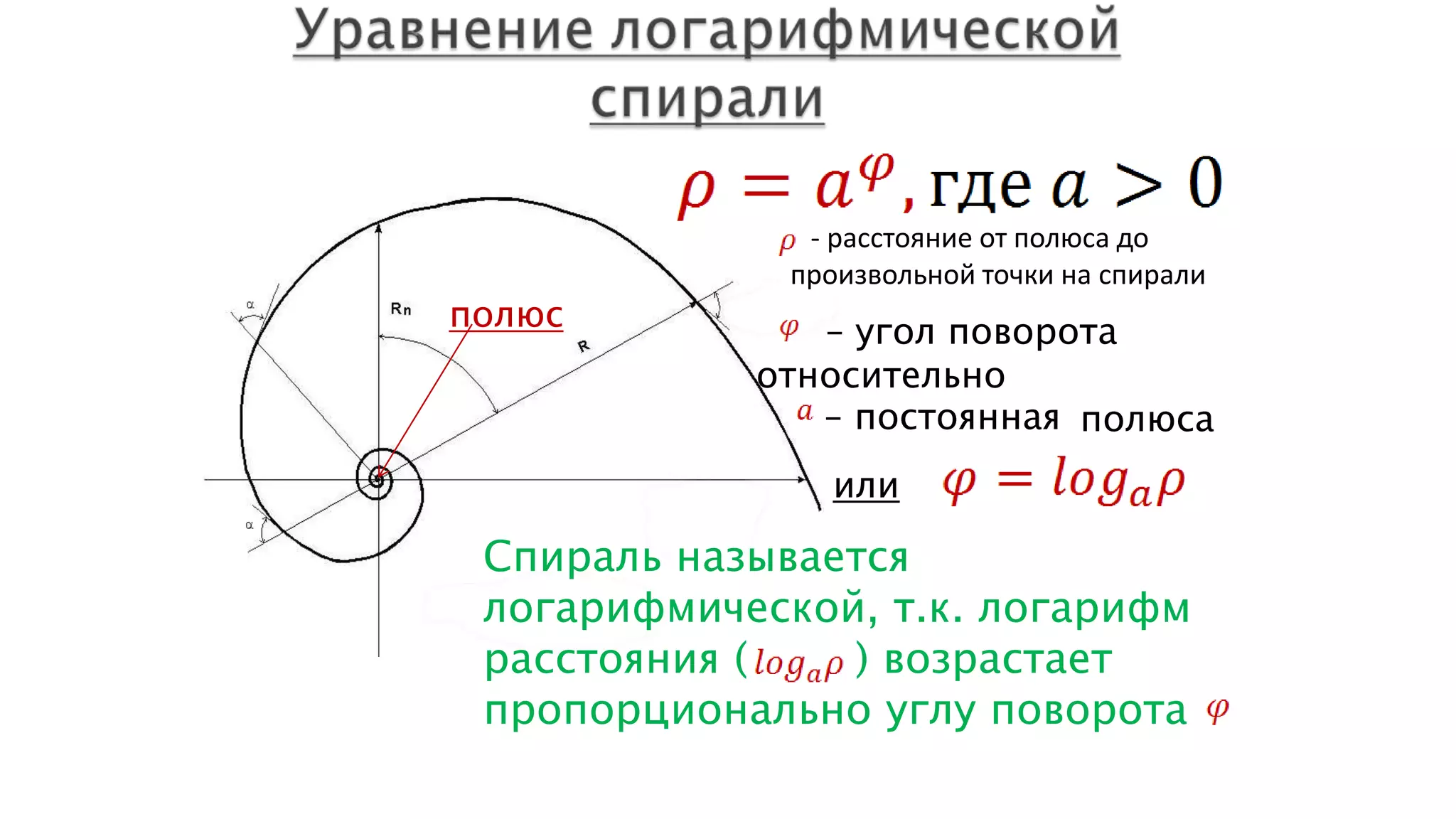
Документ обсуждает логарифмические функции и уравнения, предоставляя различные методы их решения, такие как метод потенцирования, введение новой переменной и графический метод. Он включает примеры простейших логарифмических уравнений и стратегии преобразования уравнений для нахождения их корней. В документе также рассматривается логарифмическая спираль и ее свойства.