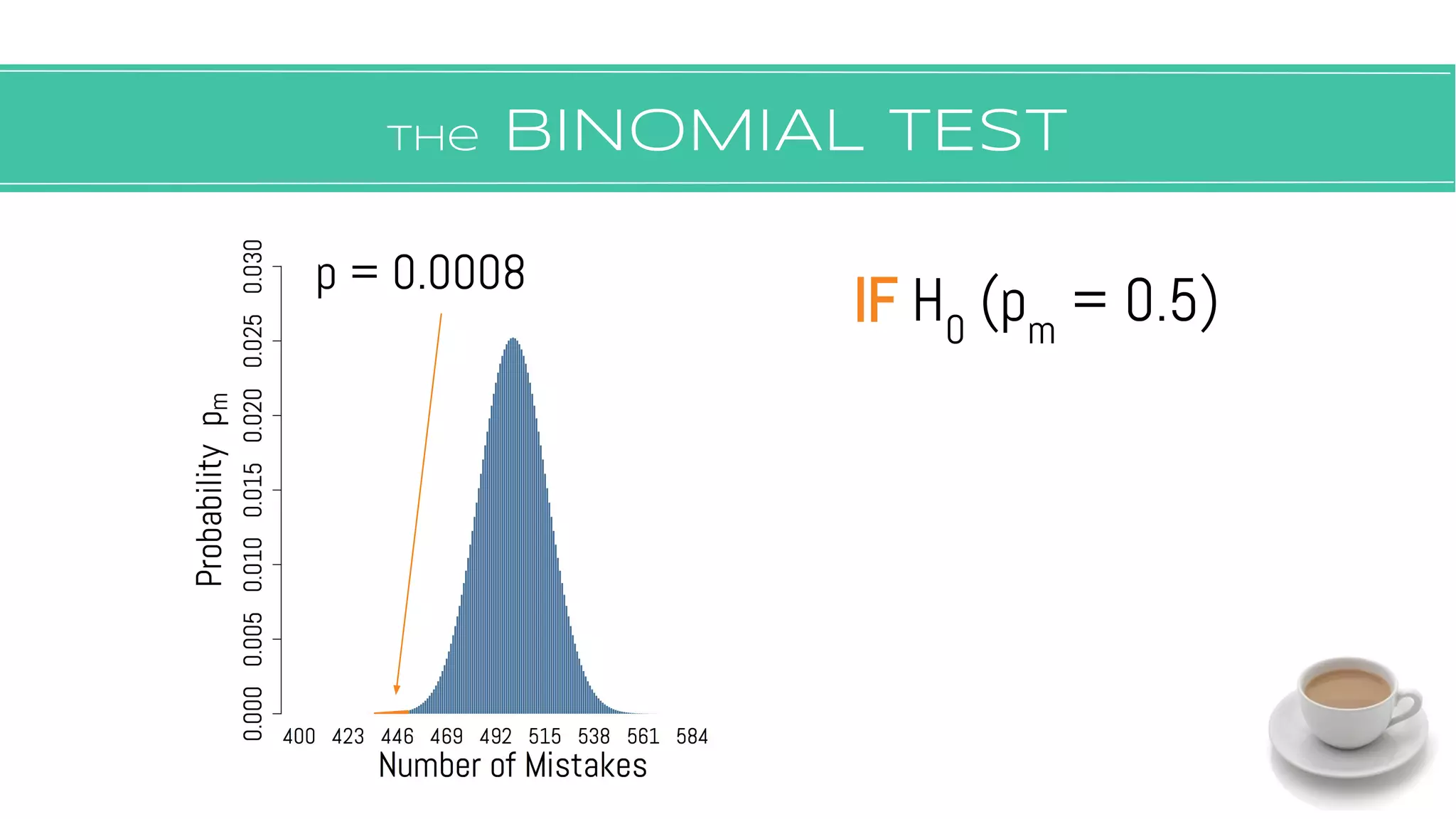
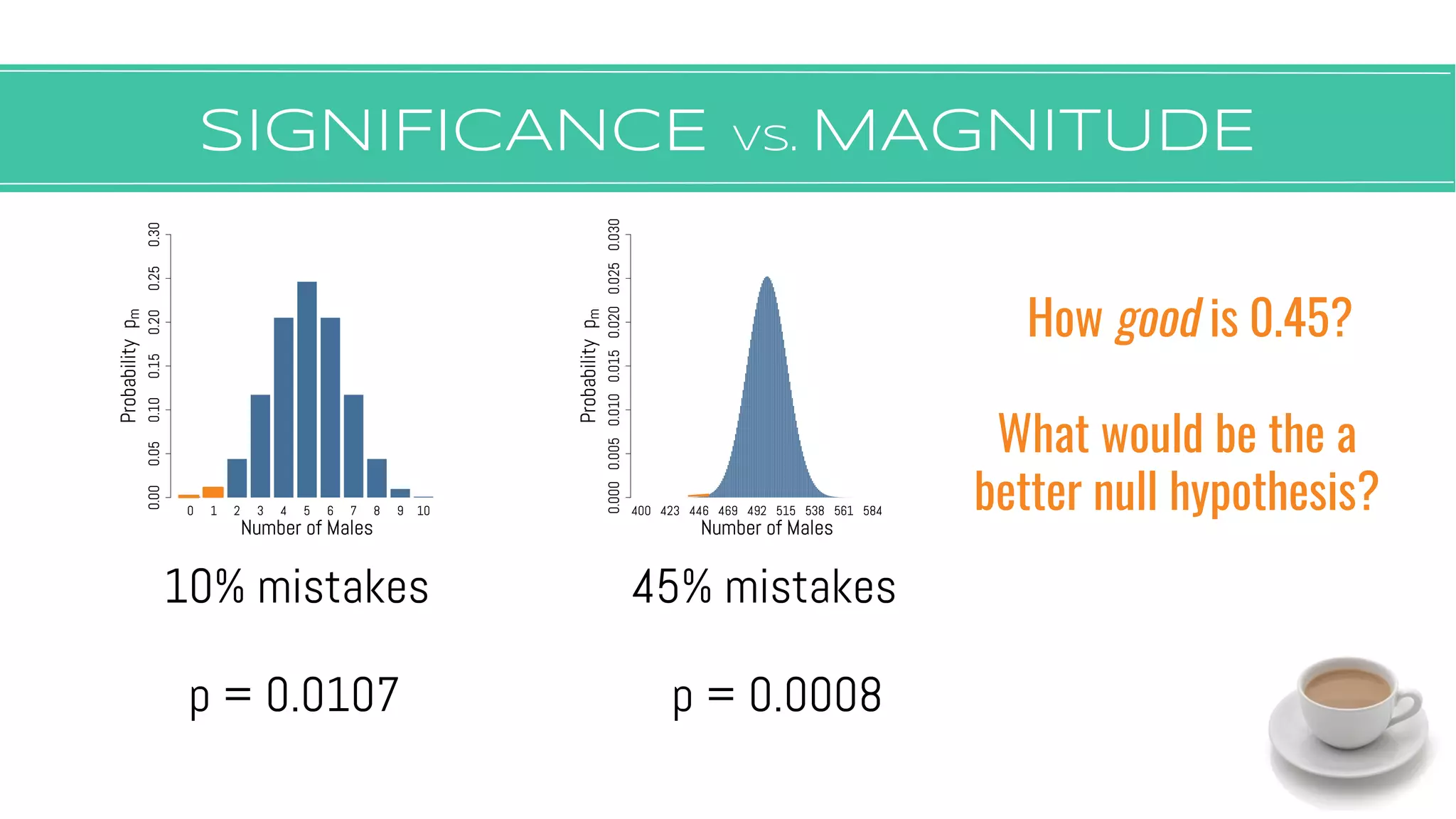
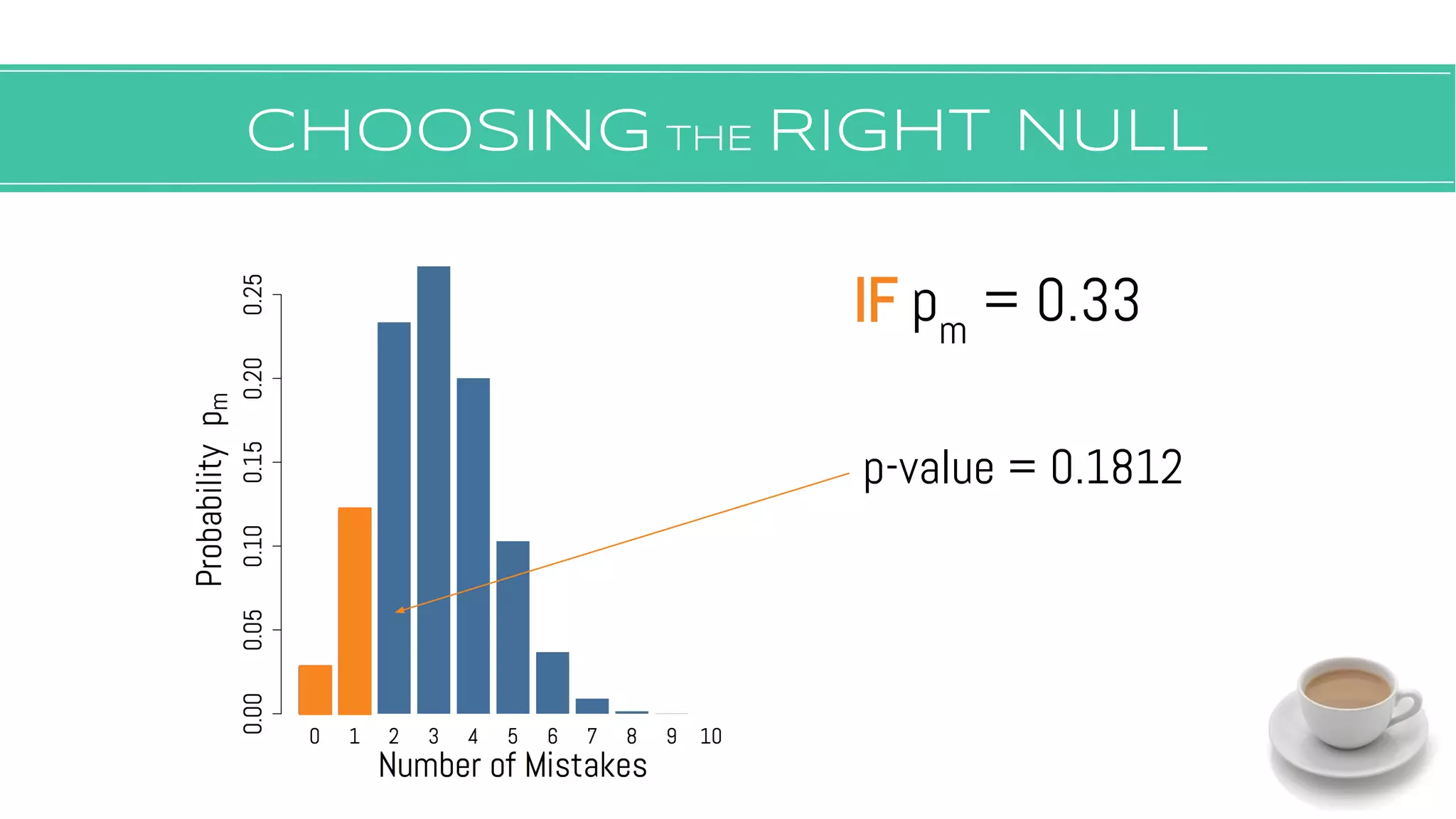
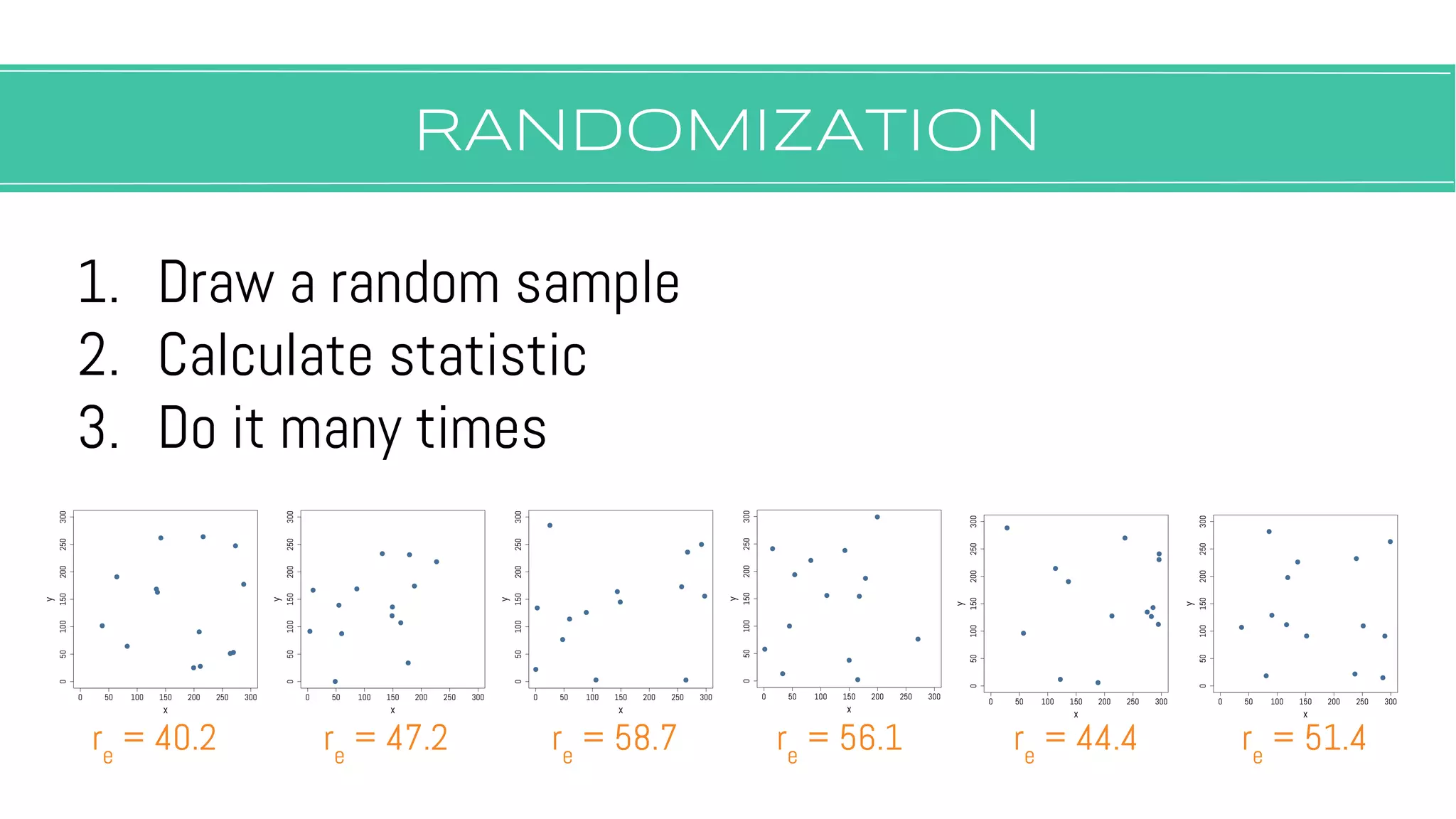
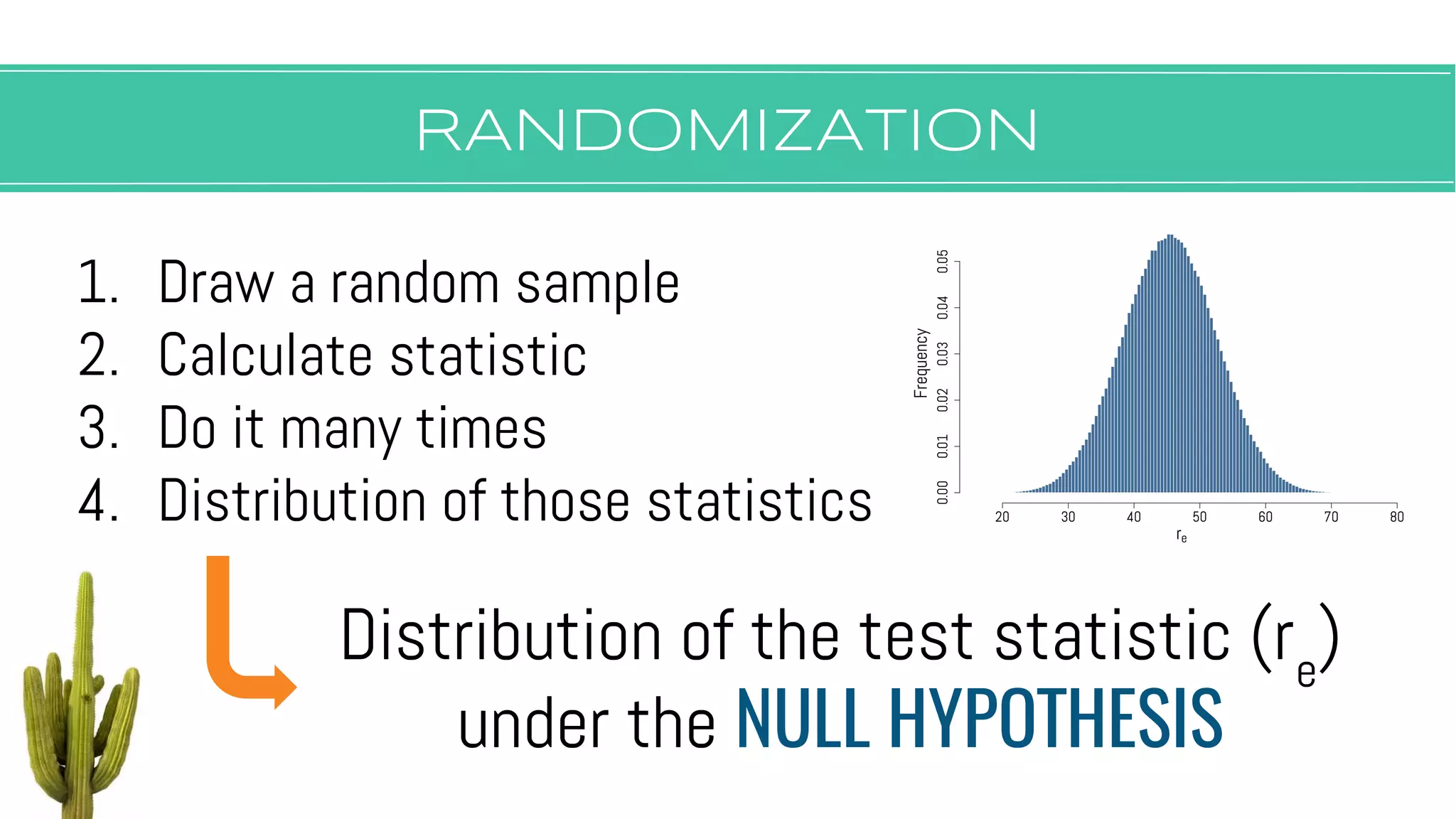
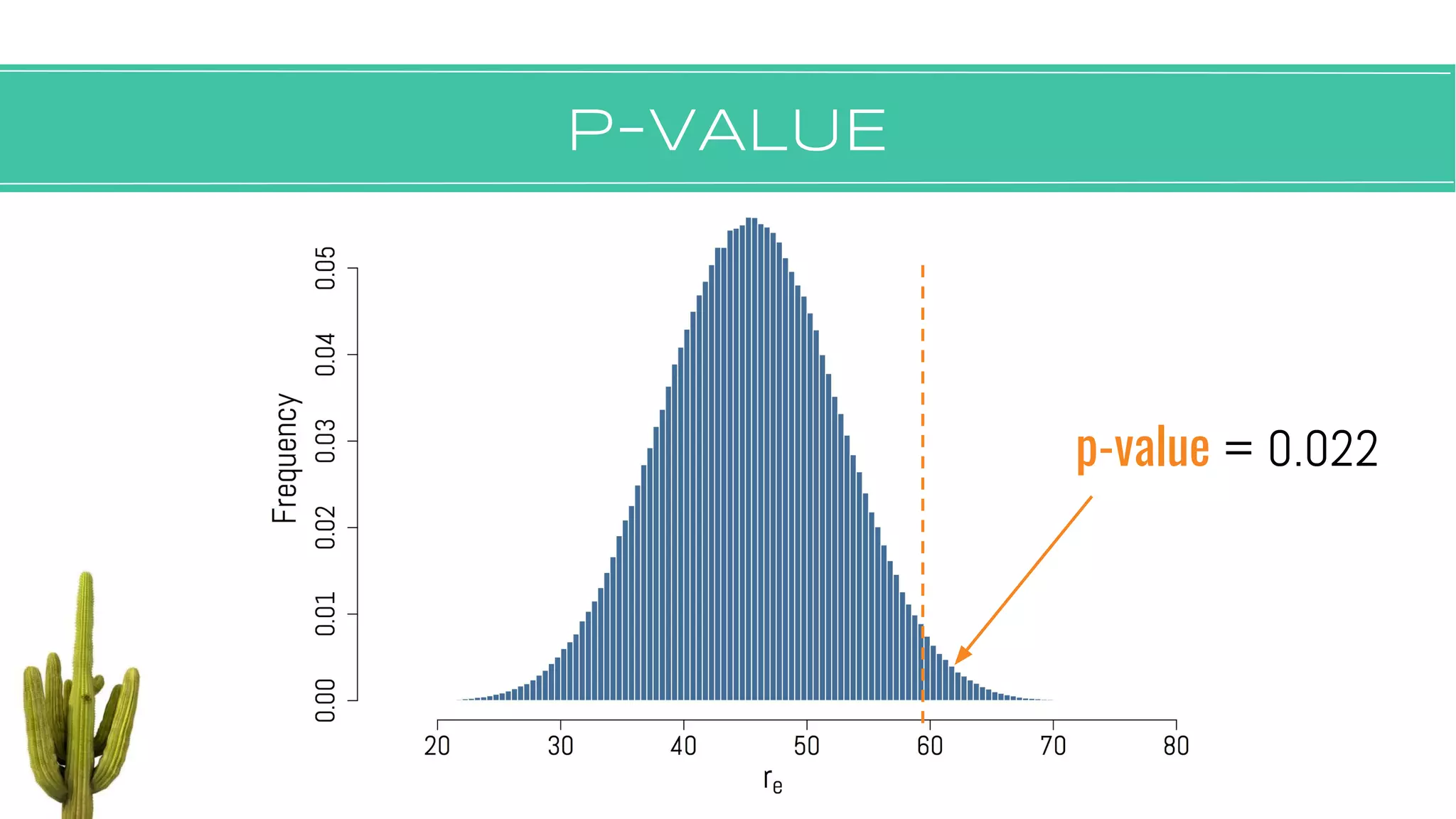
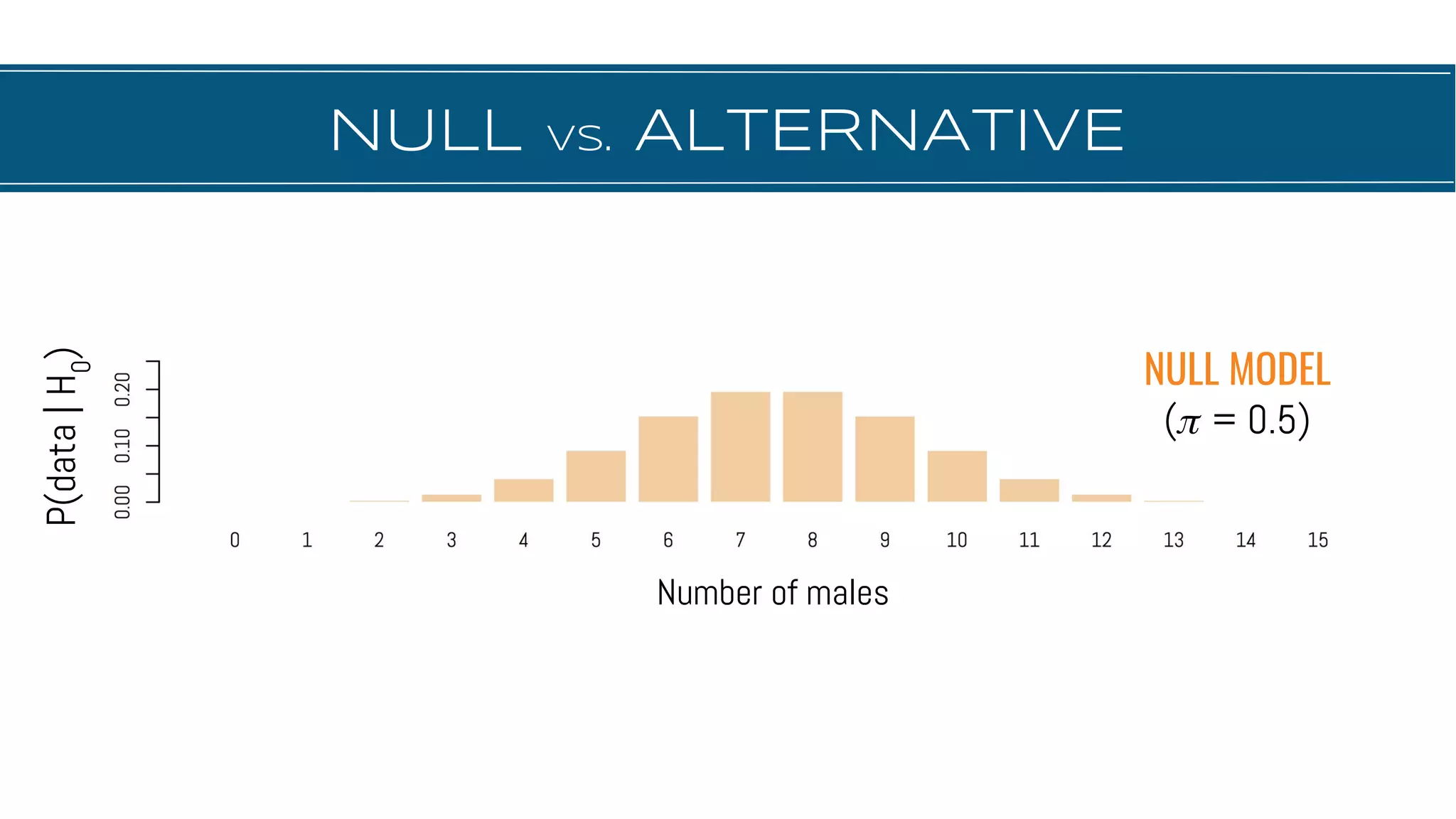
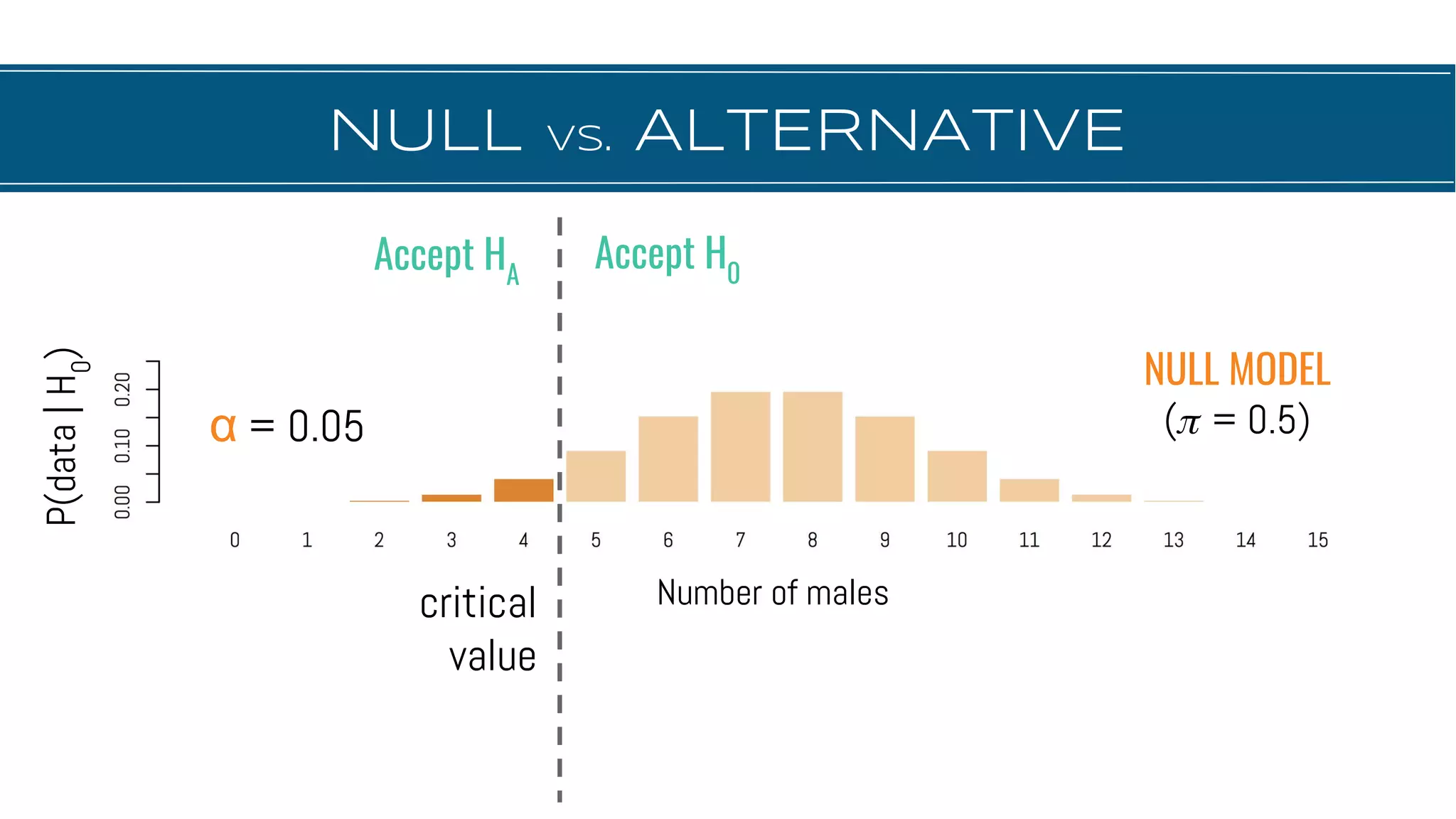
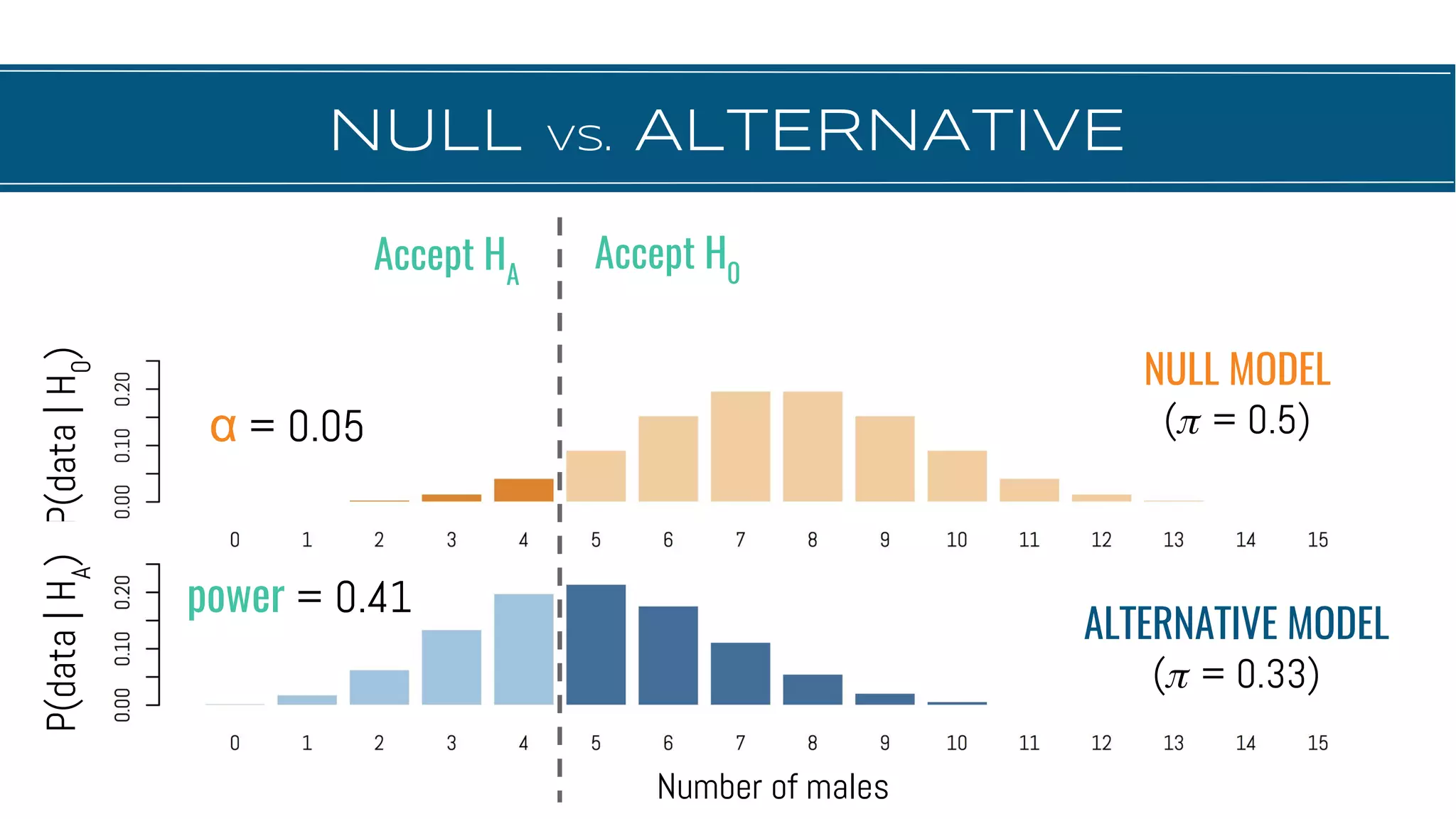
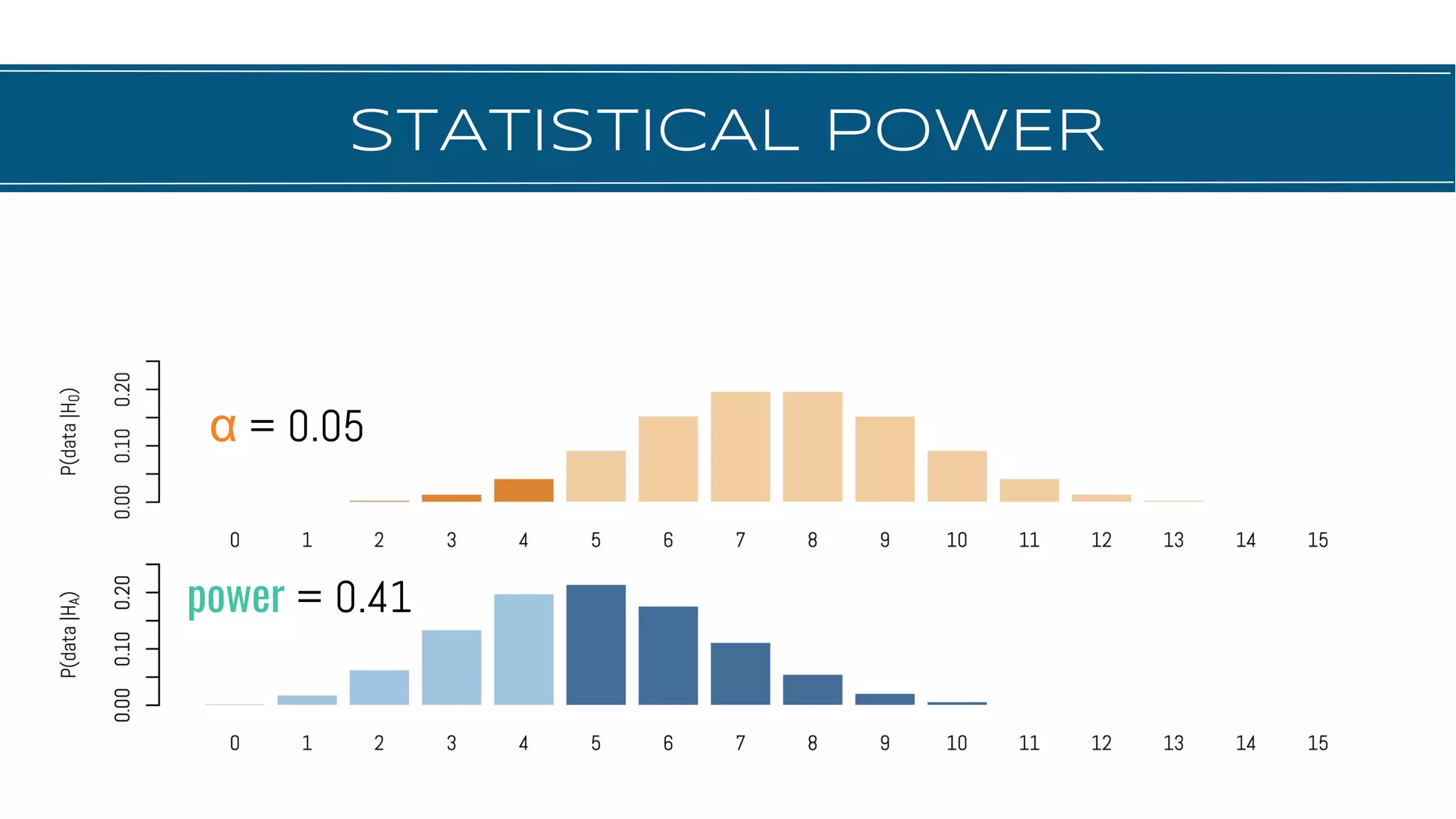
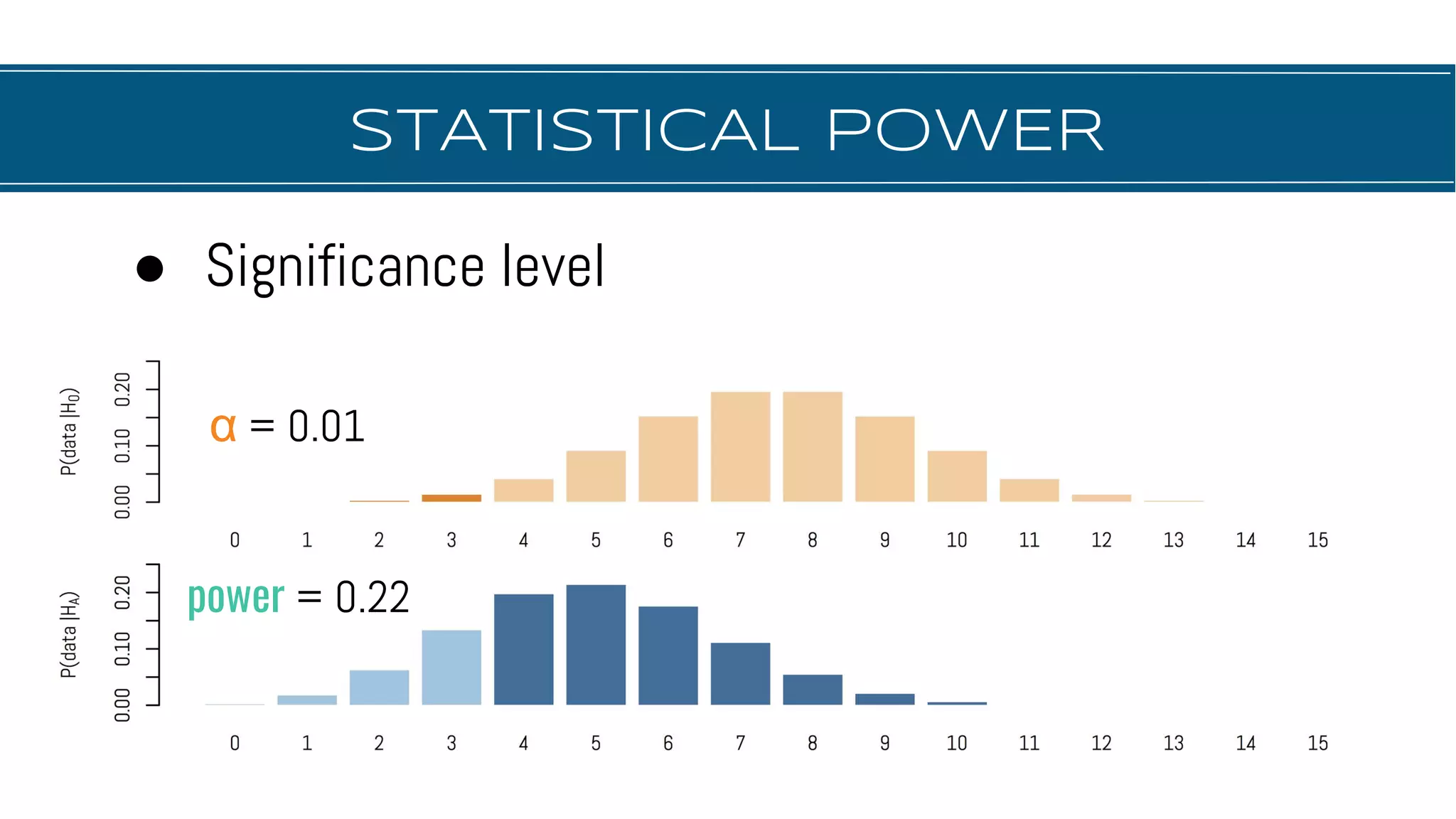
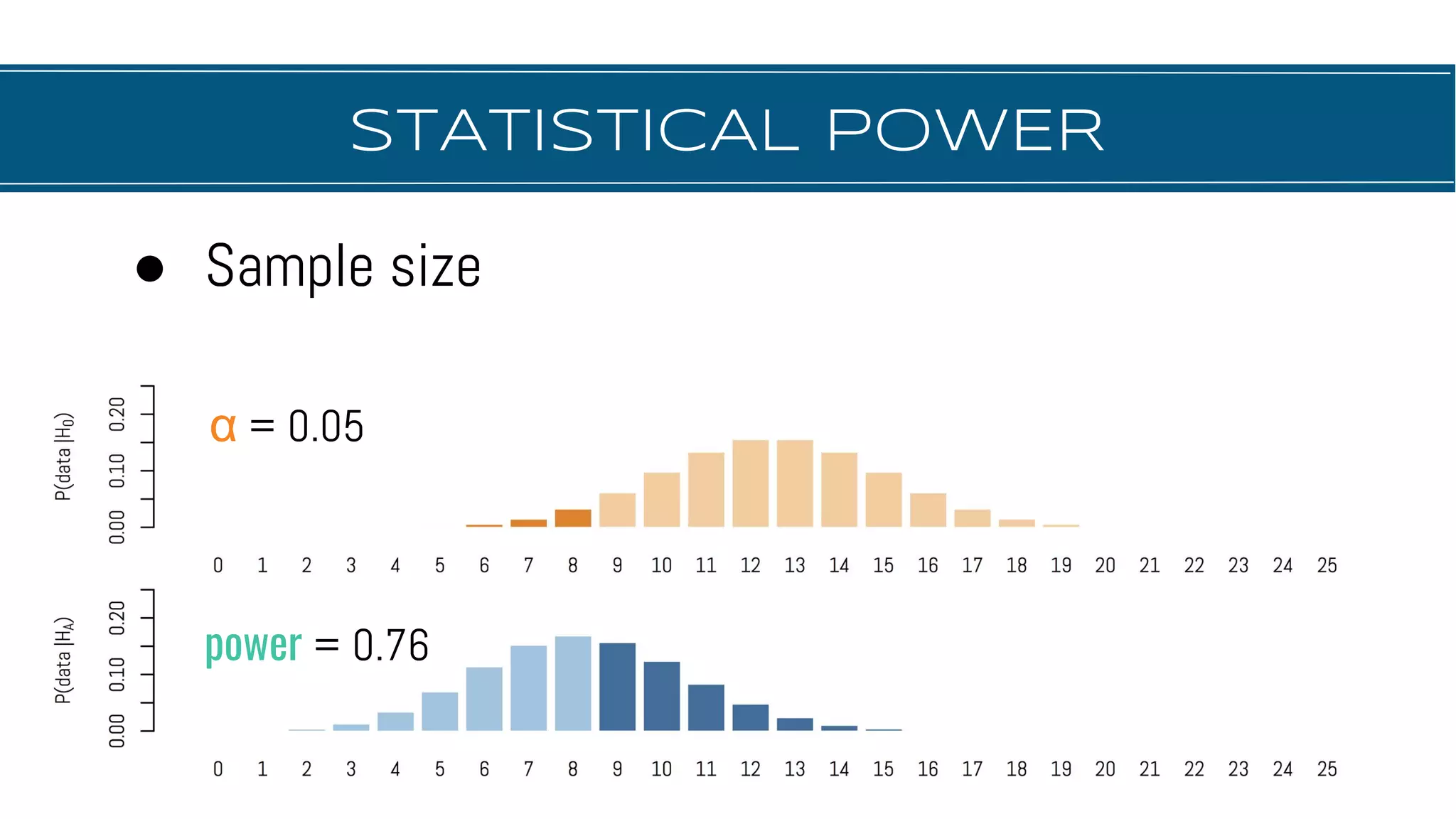
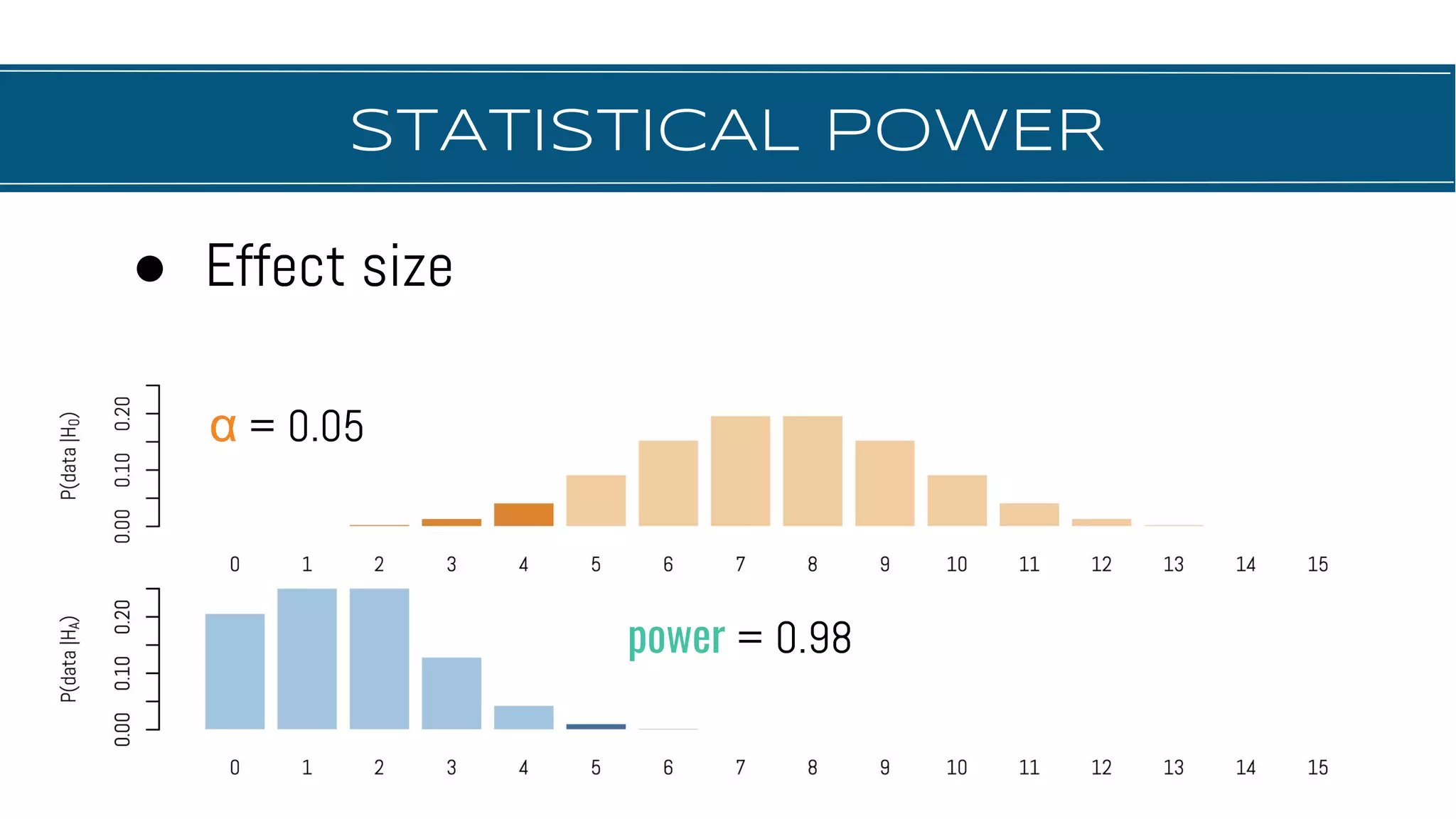
The document discusses hypothesis testing, focusing on aspects such as null and alternative hypotheses, significance testing, and the limitations of p-values. It highlights the importance of properly defining null models, statistical power, and the difference between statistical significance and effect size. Additionally, it provides examples and questions for applying nonparametric tests in biological research.

1. HYPOTHESIS TESTING

2. HYPOTHESIS TESTING
1. Science and Falsification
2. Significance Testing
2.1. What is a p-value?
2.2. How to build a Null Hypothesis
3. How about the Alternative Hypothesis?
3.1. False Alarms and Power

3. FALSIFICATIONISM
● Denying the consequent (modum tollens)
((P → Q) ^ ￢Q) → ￢P
(model → data) ^ ￢data) → ￢model
● Models can only be disproven
● Not explicitly probabilistic

4. STATISTICAL FALSIFICATIONISM
● Data is a consequence of the true model
● That consequence is probabilistic
Likelihood (Model) = P(Data | Model)
● Model unlikely if data obtained would have low
probability under that model.

5. tHE LADY
DRINKING TEA
Does tea taste different when the milk, instead of the tea, is poured first?

6. TEST INGREDIENTS
● A hypothesis to reject: the null model (H0
)
● Some data
● A summary of the data: a statistic
● A way to calculate the probability
distribution of the statistic given H0
NULL HYPOTHESIS SIGNIFICANCE TESTING

7. NHST
Null model (H0
)
Parameter
Data (X)
Statistic
Probability

8. NHST
Null model (H0
)
Parameter
Data (X)
Statistic
Probability
Null model (H0
) Lady can’t tell the difference
Parameter Probability of mistake (pm
= 0.5)
Data (X) 1 mistake out of 10 (n = 10)
Statistic Proportion of mistakes (Pm
=0.1)
Probability What is the probability of 1/10 mistakes
if H0
is true and pm
= 0.5?

9. The BINOMIAL DISTRIBUTION

10. WHITEBOARD TIME!

11. pr
(1-p)n-rn!
r! (n-r)!P(r, n | p ) =
What is the probability of making
r mistakes out of n trials given p?
p = probability of mistake r = number of mistakes
n = number of trials

12. The BINOMIAL TEST
Probability of 1 or less
mistakes= 0.0107
IF H0
(pm
= 0.5)
p-value
0.0009
0.0098
0.0439
0.1171
0.2051
0.2461
0.1171
0.2051
0.0439
0.0098
0.0009

13. P-vALUES
● NOT the probability of the null hypothesis being true

14. P-vALUES
● NOT the probability of the null hypothesis being true
● NOT applicable to all distributions

15. P-vALUES
● NOT the probability of the null hypothesis being true
● NOT applicable to all distributions
● NOT a measure of effect size or importance

16. NHST
Null model (H0
) Lady can’t tell the difference
Parameter Probability of mistake (pm
= 0.5)
Data (X) 450 mistakes out of 1000 (n = 1000)
Statistic Proportion of mistakes (Pm
= 0.45)
P-value What is the probability of making
≤ 450/1000 mistakes if pm
= 0.5?

17. The BINOMIAL TEST
p = 0.0008
IF H0
(pm
= 0.5)

18. P-vALUES
● NOT the probability of the null hypothesis being true
● NOT applicable to all distributions
● NOT a measure of effect size or importance
● ANY effect will be significant given enough data

19. SIGNIFICANCE VS. MAGNITUDE
10% mistakes
p = 0.0008p = 0.0107
45% mistakes
How good is 0.45?
What would be the a
better null hypothesis?

20. NHST
Null model (H0
) One in three mistakes
Parameter Probability of mistake (pm
= 0.33)
Data (X) 1 mistake out of 10 (n = 10)
Statistic Proportion of mistakes (Pm
=0.1)
P-value What is the probability of making
≤1/10 mistakes if pm
= 0.33?

21. CHOOSING THE RIGHT NULL
p-value = 0.1812
IF pm
= 0.33

22. SAGUAROS
iN SPACE
Do individuals distribute randomly in space?

23. PLAY
TIME!

24. RANDOMIZATION
1. Draw a random sample

25. RANDOMIZATION
1. Draw a random sample
2. Calculate statistic
3. Do it many times
re
= 40.2 re
= 47.2 re
= 58.7 re
= 56.1 re
= 44.4 re
= 51.4

26. RANDOMIZATION
1. Draw a random sample
2. Calculate statistic
3. Do it many times
re
= 40.2 re
= 47.2 re
= 58.7 re
= 56.1 re
= 44.4 re
= 51.4

27. RANDOMIZATION
1. Draw a random sample
2. Calculate statistic
3. Do it many times
4. Distribution of those statistics
Distribution of the test statistic (re
)
under the NULL HYPOTHESIS

28. P-VALUE
p-value = 0.022

29. NON-PARAMETRICPARAMETRIC
● Null model defined by
functions & parameters
● Null model constructed
through algorithms

30. P-vALUES
● NOT the probability of the null hypothesis being true
● NOT applicable to all distributions
● NOT a measure of effect size or importance
● NOT appropriate for modeling rare events

31. What is the probability of a Scientist winning a (science)
Nobel Prize?
P(Nobel | Scientist) = 0.00001
Marie Curie won 2 Nobel Prizes
p-value = P(≥2 Nobel | Scientist) ≅ 0.00000000001
Therefore, Marie Curie is unlikely to be a Scientist?
WHY IS THIS WRONG?

32. CONSIDERING the ALTERNATIVE
Probability of a Scientist winning a Nobel Prize?
P(2 Nobel | Scientist) = 0.000012
P(2 Nobel |￢ Scientist) ≅ 0.000000000012
Likelihood of
being a scientist
Likelihood of
NOT being a scientist
LIKELIHOOD RATIO = = 1012
0.000000000012
0.000012

33. NULL vs. ALTERNATIVE
H0
is true Ha
is true
Accept H0 ✓ Type II error
Accept Ha
Type I error ✓
● Consider both a NULL and an ALTERNATIVE hypothesis

34. NULL vs. ALTERNATIVE
H0
is true Ha
is true
Accept H0
1 − α 1 − β
Accept Ha
α β
False Positives
You’re
pregnant
POWER

35. JEWEL WASP
{Nasonia vitripennis}
EXTREME
SEX RATIOS
Do jewel wasps differ from the Fisherian (1:1) sex ratio?

36. Null model (H0
)
Parameter
Data (X)
Statistic
Probability
inspired by
Hamilton 1967.
Science

37. Null model (H0
) Even sex ratio (1:1)
Parameter Probability of producing a male ( = 0.5)
Data (X) Number of males and females (n = 15)
Statistic Proportion of males
Probability
inspired by
Hamilton 1967.
Science

38. Null model (H0
) Even sex ratio (1:1)
Parameter Probability of producing a male ( = 0.5)
Data (X) Number of males and females (n = 15)
Statistic Proportion of males
Alternative (HA
)
Model
inspired by
Hamilton 1967.
Science

39. Null model (H0
) Even sex ratio (1:1)
Parameter Probability of producing a male ( = 0.5)
Data (X) Number of males and females (n = 15)
Statistic Proportion of males
Alternative (HA
) Biased sex ratio (1:2)
Model Probability of producing a male ( = 0.33)
inspired by
Hamilton 1967.
Science

40. NULL vs. ALTERNATIVE
NULL MODEL
( = 0.5)
Number of males
P(data|H0
)

41. NULL vs. ALTERNATIVE
α = 0.05
P(data|H0
)
critical
value
NULL MODEL
( = 0.5)
Number of males
Accept HA
Accept H0

42. NULL vs. ALTERNATIVE
α = 0.05
P(data|H0
)
NULL MODEL
( = 0.5)
power = 0.41
Number of males
ALTERNATIVE MODEL
( = 0.33)
Accept HA
Accept H0
P(data|HA
)

43. WHAT GIVES
POWER?

44. STATISTICAL POWER
power = 0.41
α = 0.05

45. STATISTICAL POWER
power = 0.22
● Significance level
α = 0.01

46. STATISTICAL POWER
power = 0.76
● Sample size
α = 0.05

47. STATISTICAL POWER
power = 0.98
● Effect size
α = 0.05

48. Type I errorp-value
● Refers to single test
● Data-based random value
● Property of the data
● Inductive evidence
● Refers to multiple tests
● Fixed quantity set a priori
● Property of the test
● Deductive assessment
FISHER’s APPROACH NEYMAN-PEARSON APPROACH

49. UNDERSTANDING TESTS

50. STATISTICAL TESTS
● Sign test
● Mann-Whitney’s U
● Wilcoxon signed-rank test
● Siegel-Tukey test
● Mantel Test
● Permutation Test

51. HOMEWORK

52. HOMEWORK
● Work in groups
● Read one of the assigned articles applying a
nonparametric test in biological research
● Try to understand the test in question
● Present your findings to the class
30.01.17
10:00h

53. QUESTIONS
1. What is the question? What is the purpose of the test?
2. What is the statistic and what does it measure?
3. How is the null hypothesis built and what does it assume?
4. How does the test answer the question?
5. Find out how to implement the test in R
6. What other applications could this test have?

54. PRESENTATIONS
6 questions = 6 slides = 6 minutes

55. EvALUATION
● Questions: Relate lecture concepts to the new test
● Delivery: Quality and clarity of the presentation
● Discussion: Both asking and answering questions
● Group-level AND individual-level
Group work ≠ Dividing tasks
(except in presenting)