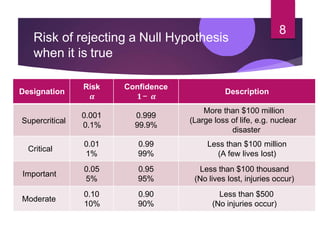
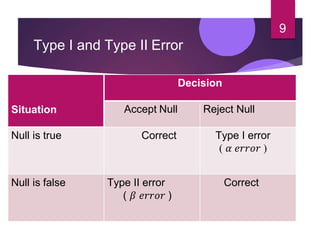
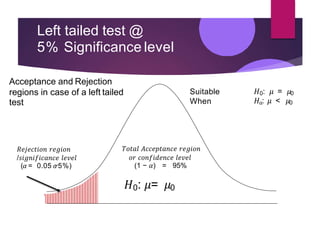
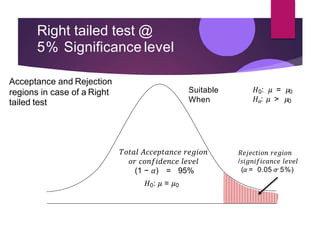
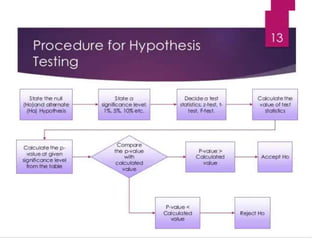
Hypothesis testing involves setting up a null hypothesis and alternative hypothesis, determining a significance level, calculating a test statistic, identifying the critical region, computing the test statistic value based on a sample, and making a decision to reject or fail to reject the null hypothesis. The z-test is used when the sample size is large and the population standard deviation is known, while the t-test is used for small samples when the population standard deviation is unknown. Both tests involve calculating a test statistic and comparing it to critical values to determine if there is sufficient evidence to reject the null hypothesis. Limitations include that the tests only indicate differences and not the reasons for them, and inferences are based on probabilities rather than certainty.

1. Hypothesis Testing;

2. What is Hypothesis?
Hypothesis is a predictive statement, capable of being
tested by scientific methods, that relates an independent
variables to some dependent variable.
A hypothesis states what we are looking for and it is a
proportion which can be put to a test to determine its
validity
e.g.
Students who receive counseling will show a greater increase
in creativity than students not receiving counseling

3. Characteristics of Hypothesis
Clear and precise.
Capable of being tested.
Stated relationship between variables.
limited in scope and must be specific.
Stated as far as possible in most simple terms so that the same is easily
understand by all concerned. But one must remember that simplicity of
hypothesis has nothing to do with its significance.
Consistent with most known facts.
Responsive to testing with in a reasonable time. One can’t spend a life time
collecting data to test it.
Explain what it claims to explain; it should have empirical reference.

4. Null Hypothesis
It is an assertion that we hold as true unless we
have sufficient statistical evidence to conclude
otherwise.
Null Hypothesis is denoted by 𝐻0
If a population mean is equal to hypothesised
mean then Null Hypothesis can be written as
𝐻0: 𝜇 = 𝜇0

5. Alternative Hypothesis
The Alternative hypothesis is negation of null hypothesis and is
denoted by 𝐻𝑎
If Null is given as
𝐻0: 𝜇= 𝜇0
Then alternative Hypothesis can be written as
𝐻𝑎: 𝜇 ≠ 𝜇0
𝐻𝑎: 𝜇 > 𝜇0
𝐻𝑎: 𝜇 < 𝜇0

7. Level of significance and
confidence
Significance means the percentage risk to
reject a null hypothesis when it is true and
it is denoted by 𝛼. Generally taken as 1%,
5%, 10%
(1 − 𝛼) is the confidence interval in
which the null hypothesis will exist
when it is true.

8. Risk of rejecting a Null Hypothesis
8
when it is true
Designation
Risk
𝜶
Confidence
𝟏− 𝜶
Description
Supercritical
0.001
0.1%
0.999
99.9%
More than $100 million
(Large loss of life, e.g. nuclear
disaster
Critical
0.01
1%
0.99
99%
Less than $100 million
(A few lives lost)
Important
0.05
5%
0.95
95%
Less than $100 thousand
(No lives lost, injuries occur)
Moderate
0.10
10%
0.90
90%
Less than $500
(No injuries occur)

9. Type I and Type II Error
Situation
Decision
Accept Null Reject Null
Null is true Correct Type I error
( 𝛼 𝑒𝑟𝑟𝑜𝑟 )
Null is false Type II error
( 𝛽 𝑒𝑟𝑟𝑜𝑟 )
Correct
9

10. Two tailed test @
5% Significance level
Acceptance and Rejection
regions in case of a Two
tailed test
𝑅𝑒𝑗𝑒𝑐𝑡𝑖𝑜𝑛 𝑟𝑒𝑔𝑖𝑜𝑛
/𝑠𝑖𝑔𝑛𝑖𝑓𝑖𝑐𝑎𝑛𝑐𝑒 𝑙𝑒𝑣𝑒𝑙
(𝛼 = 0.025 𝑜
𝑟 2.5%)
𝑅𝑒𝑗𝑒𝑐𝑡𝑖𝑜𝑛 𝑟𝑒𝑔𝑖𝑜𝑛
/𝑠𝑖𝑔𝑛𝑖𝑓𝑖𝑐𝑎𝑛𝑐𝑒 𝑙𝑒𝑣𝑒𝑙
(𝛼 = 0.025 𝑜𝑟 2.5%)
Suitable
When
𝐻0: 𝜇 = 𝜇0
𝐻𝑎: 𝜇 ≠ 𝜇0
𝑇𝑜𝑡𝑎𝑙 𝐴𝑐𝑐𝑒𝑝𝑡𝑎𝑛𝑐𝑒 𝑟𝑒𝑔𝑖𝑜𝑛
𝑜𝑟 𝑐𝑜𝑛𝑓𝑖𝑑𝑒𝑛𝑐𝑒 𝑙𝑒𝑣𝑒𝑙
(1 − 𝛼) = 95%
𝐻0: 𝜇 = 𝜇0

11. Left tailed test @
5% Significance level
Acceptance and Rejection
regions in case of a left tailed
test
𝐻0: 𝜇= 𝜇0
𝑇𝑜𝑡𝑎𝑙 𝐴𝑐𝑐𝑒𝑝𝑡𝑎𝑛𝑐𝑒 𝑟𝑒𝑔𝑖𝑜𝑛
𝑜𝑟 𝑐𝑜𝑛𝑓𝑖𝑑𝑒𝑛𝑐𝑒 𝑙𝑒𝑣𝑒𝑙
(1 − 𝛼) = 95%
𝑅𝑒𝑗𝑒𝑐𝑡𝑖𝑜𝑛 𝑟𝑒𝑔𝑖𝑜𝑛
/𝑠𝑖𝑔𝑛𝑖𝑓𝑖𝑐𝑎𝑛𝑐𝑒 𝑙𝑒𝑣𝑒𝑙
(𝛼 = 0.05 𝑜
𝑟5%)
Suitable
When
𝐻0: 𝜇 = 𝜇0
𝐻𝑎: 𝜇 < 𝜇0

12. Right tailed test @
5% Significance level
Acceptance and Rejection
regions in case of a Right
tailed test
Suitable
When
𝐻0: 𝜇 = 𝜇0
𝐻𝑎: 𝜇 > 𝜇0
𝑇𝑜𝑡𝑎𝑙 𝐴𝑐𝑐𝑒𝑝𝑡𝑎𝑛𝑐𝑒 𝑟𝑒𝑔𝑖𝑜𝑛
𝑜𝑟 𝑐𝑜𝑛𝑓𝑖𝑑𝑒𝑛𝑐𝑒 𝑙𝑒𝑣𝑒𝑙
(1 − 𝛼) = 95%
𝐻0: 𝜇 = 𝜇0
𝑅𝑒𝑗𝑒𝑐𝑡𝑖𝑜𝑛 𝑟𝑒𝑔𝑖𝑜𝑛
/𝑠𝑖𝑔𝑛𝑖𝑓𝑖𝑐𝑎𝑛𝑐𝑒 𝑙𝑒𝑣𝑒𝑙
(𝛼 = 0.05 𝑜
𝑟 5%)

14. Hypothesis testingsteps
Setting up Hypothesis
Setting up suitable significancelevel
Determination of a test statistic
Determination of critical region
Computing the value of teststatistics
Making Decision

15. Hypothesis testingsteps
• Setting up of a hypothesis:
– Hypothesis are generally assumptionsabout
the value of the populationparameter.
– Hypothesis specifies a single value or a range of values for
two different hypothesis rather than constructing a single
hypothesis. These hypothesis are
• H = Null Hypothesis
0
• H1 = Alternate Hypothesis
– A null hypothesis is set as the hypothesis of no
relationship between those two variables;
whereas the alternative hypothesis is the
hypothesis of the relationship between
variables. MakingDecision
Computingthevalue of test
statistics
Determination ofcritical
region
Determination of atest
statistic
Setting upsuitable
significancelevel
Setting upHypothesis

16. Hypothesis testing steps
• Setting up of suitable significance level:
– The level of significance is denoted by α is
chosen before drawing sample any sample. The
level of significance denotes the probability of
rejecting the null hypothesis when it istrue.
– The value of α varies from problem to problem, but
usually it is taken as either 5 percent or 1 percent.
– A 5 percent level of significance means that there
are 5 chances out of hundred that a null hypothesis
will get rejected when it should be accepted. This
means that the researcher is 95 percent confident
that a right decision has beentaken.
Determination ofcritical
region
Computingthevalue of test
statistics
Making Decision
Determination of atest
statistic
Setting upsuitable
significancelevel
Setting upHypothesis

17. Hypothesis testing steps
• Determination of a test
statistic:
– The next step is to determine a
suitable test statistic and its
distribution. Aswould be seen later
,
the test statistic could be t,Z,
2
or F
, depending upon various
Setting upsuitable
significancelevel
Determination of atest
statistic
Determination ofcritical
region
Computingthevalue of test
statistics
Making Decision
Setting upHypothesis

18. Hypothesis testing steps
• Determination of critical region:
– Before a sample is drawn from the population,
it is very important to specify the values of test
statistic that will lead to rejection or acceptance
of the null hypothesis. The one that leads to the
rejection of the null hypothesis is called the
critical region.
– Given a level of significance, α, the optimal
critical region for a two-tailed test consists of
that α/2 percent area in the right hand tail of
the distribution plus that α/2 percent in the left
hand tail of the distribution where that null
hypothesis is rejected.
Computingthevalue of test
statistics
Making Decision
Determination ofcritical
region
Determination of atest
statistic
Setting upsuitable
significancelevel
Setting upHypothesis

19. Hypothesis testing steps
• Computing the value of
test- statistic:
– The next step is to compute the value
of the test statistic based upon
random sample size n. Once the value
of test statistic is computed, oneneeds
to examine whether the sampleresults
fall in the critical region or in the
acceptance region.
Computingthevalue of test
statistics
Making Decision
Determination ofcritical
region
Determination of atest
statistic
Setting upsuitable
significancelevel
Setting upHypothesis

20. Hypothesis testing steps
• Making Decision:
– The hypothesis may be rejected or accepted
depending upon whetherthe value of the test
statistic falls in the rejection or the
acceptance region
. Management decisions are based
upon the statistical decision of either
rejecting or accepting the null
hypothesis.
Determination ofcritical
region
Computingthevalue of test
statistics
Making Decision
Determination of atest
statistic
Setting upsuitable
significancelevel
Setting upHypothesis

21. Hypothesis Testing
of Means Z-TEST AND T-TEST

22. Hypothesis testing
• T
eststatistic for testing
Hypothesis about
Population mean: incase
sample size is large
(n>30),Z statistic would
be used. For a small
sample size(n≤30) a
further question
regarding the knowledge
of population standard
deviation() isasked.
Sample size
Knowledge of
population standard
deviation ()
Known Not Known
Large
(n>30)
Z Z
Small
(n≤30)
Z t

23. T test
The t-test is a test in statistics that is used for testing hypotheses regarding the
mean of a small sample taken population when the standard deviation of the
population is not known.
•The t-test is used to determine if there is a significant difference between the
means of two groups.
•The t-test is used for hypothesis testing to determine whether a process has
an effect on both samples or if the groups are different from each other.
•Basically, the t-test allows the comparison of the mean of two sets of data and
the determination if the two sets are derived from the same population.
•After the null and alternative hypotheses are established, t-test formulas are
used to calculate values that are then compared with standard values.
•Based on the comparison, the null hypothesis is either rejected or accepted.
•The T-test is similar to other tests like the z-test and f-test except that t-test is
usually performed in cases where the sample size is small (n≤30).

24. T-test formula
T-tests can be performed either manually by using a formula or through some
software.
The formula for the manual calculation of t-value is given below:
where x
̅ is the mean of the sample, and µ is the assumed mean, σ is the
standard deviation, and n is the number of observations.
T-test for the difference in mean:
where x
̅ 1 and x
̅ 2 are the mean of two samples and σ1 and σ2 is the standard
deviation of two samples, and n1 and n2 are the numbers of observation of two
samples.

25. z-test
•z-test is a statistical tool used for the comparison or determination of the
significance of several statistical measures, particularly the mean in a
sample from a normally distributed population or between two
independent samples.
•Like t-tests, z tests are also based on normal probability distribution.
•Z-test is the most commonly used statistical tool in research
methodology, with it being used for studies where the sample size is large
(n>30).
•In the case of the z-test, the variance is usually known.
•Z-test is more convenient than t-test as the critical value at each
significance level in the confidence interval is the sample for all sample
sizes.
•A z-score is a number indicating how many standard deviations above or
below the mean of the population is.

26. z-test formula
For the normal population with one sample:
where x
̄ is the mean of the sample, and µ is the assumed mean, σ is the
standard deviation, and n is the number of observations.
z-test for the difference in mean:
where x
̄ 1 and x
̄ 2 are the means of two samples, σ is the standard deviation of
the samples, and n1 and n2 are the numbers of observations of two samples.

29. Limitations of the test of
Hypothesis
Testing of hypothesis is not decision making itself; but help for
decision making
Test does not explain the reasons as why the difference
exist, it only indicate that the difference is due to fluctuations
of sampling or because of other reasons but the tests do not
tell about the reason causing the difference.
Tests are based on the probabilities and as such cannot be
expressed with full certainty.
Statistical inferences based on the significance tests
cannot be said to be entirely correct evidences
concerning the truth of the hypothesis.