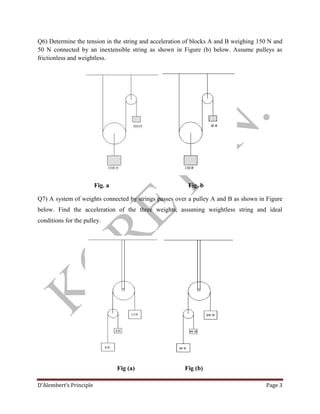
D'Alembert's Principle states that the resultant of all external forces and inertia forces acting on a body is zero for the body to be in dynamic equilibrium. Inertia forces are represented as minus mass times acceleration. The principle allows equations of static equilibrium to be applied to bodies undergoing translational motion by considering an imaginary inertia force equal and opposite to actual inertia. Several example problems are provided applying the principle to analyze motion of connected bodies over pulleys, motion on inclined planes, and motion within elevators.

1. D’Alembert’s Principle Page 1
CHAPTER NO. 7
D’Alembert’s Principle
Q.1 What do you understand by Dynamic Equilibrium?
Ans: 1) A body move with certain acceleration due to the effect of applied force according to
the Newton’s second law. So this body cannot be in equilibrium because of the resultant
applied force. Then the equations of static equilibrium are not applicable here.
2) If now an imaginary force F = ma is applied to the body opposite to the direction of
acceleration ‘a’, then the body is said to be in dynamic equilibrium. Then all equations of
static equilibrium are applicable to dynamic equilibrium.
Q.2 State and explain D’Alembert’s Principle of dynamic equilibrium.
Ans: 1) Due to application of force or force system, a body has a motion of translation and it is
not in equilibrium.
2) D’Alembert’s suggested to write Newton’s second law Σ F = ma in the form
Σ F – ma = 0
This is the equation of the dynamic equilibrium.
Where,
Σ F = resultant of external forces and
(-ma) = D’Alembert’s inertia force.

2. D’Alembert’s Principle Page 2
Therefore, the motion of acceleration is brought to dynamic equilibrium by adding
reversed effective force (-ma) on the body.
Statement:
D’Alembert’s Principle states that, “the impressed forces acting on the body are in
dynamic equilibrium with inertia forces of the body under motion”.
3) In short, D’Alembert’s Principle states that, the resultant of external force Σ F and the
inertia force (-ma) is always zero. This is the condition of dynamic equilibrium.
------------------------------------------------------------------------------------------------------------
Type I) Analysis of the motion of two bodies connected by a string: (egs. on Pulley)
Q1) Two weights W1 and W2 are connected by a light and inextensible string, passing over a
smooth pulley. If W1 > W2. Prove that the acceleration ‘a’ of the system and tension in string are
given by,
a =
g (W1− W2)
W1+ W2
and T =
2W1 W2
W1+ W2
Q2) Two bodies of weight 50 N and 30 N are connected to the two ends of light inextensible
string. The string is passing over a smooth pulley. Determine:
a) The acceleration of the system and
b) Tension in the string (g = 9.81 m/s2
)
Q3) Two bodies of weight 300 N and 450 N are connected to two ends of light inextensible
string. The string is passing over a smooth pulley. Determine: (Assignment Problem)
a) The acceleration of the system and
b) Tension in the string (g = 9.81 m/s2
)
Q4) Two bodies of different weights are connected to two ends of light inextensible string. The
string is passing over a smooth pulley. If the acceleration of the system is 3 m/s2
and bigger
weight is 60N, determine: (Assignment Problem)
a) The smaller weight and
b) Tension in the string (g = 9.81 m/s2
)
Q5) Determine the tension in the string and acceleration of blocks A and B weighing 1500 N and
500 N connected by an inextensible string as shown in Figure (a) below. Assume pulleys as
frictionless and weightless.

3. D’Alembert’s Principle Page 3
Q6) Determine the tension in the string and acceleration of blocks A and B weighing 150 N and
50 N connected by an inextensible string as shown in Figure (b) below. Assume pulleys as
frictionless and weightless.
Fig. a Fig. b
Q7) A system of weights connected by strings passes over a pulley A and B as shown in Figure
below. Find the acceleration of the three weights, assuming weightless string and ideal
conditions for the pulley.
Fig (a) Fig (b)

4. D’Alembert’s Principle Page 4
Q8) Solve same problem for system shown in fig (b) above.
Type II) Motion on an inclined smooth surface:
Q1) A body of weight 200 N is initially stationary on a 450
inclined plane. What distance along
plane must the body slide, before it reaches a speed of 2 m/s (𝜇 = 0.1)
Q2) A motorist travelling at a speed of 70 kmph suddenly applies brakes and halts after skidding
50 m. Determine:
a) The time required to stop the car and
b) The co-efficient of friction between the tyres and the roads. (Dec 2005) (10 Mks)
Q3) Two rough planes inclined at 300
and 600
to horizontal are placed back to back as shown in
Fig below. The blocks of weights 50 N and 100 N are placed on the faces and are connected by a
string running parallel to planes and passing over a frictionless pulley. If μ =
1
3
, find the resulting
acceleration and tension in the string.
Figure (a)
Q4) Two weights 800 N and 200 N are connected by a thread and they move along a rough
horizontal plane under the action of a force 400 N applied to the 800 N weight as shown in Fig.
below. μ = 0.3. Using D’Alembert’s Principle determine the acceleration of the weight and
tension in the thread.

5. D’Alembert’s Principle Page 5
Q5) A body weighing 1200 N rests on a rough plane inclined at 120 to the horizontal. It is pulled
up the plane by means of a light flexible rope running parallel to the plane and passing over a
light frictionless pulley at the top of the plane as shown in Figure in Figure below. The portion of
the rope beyond the pulley hangs verticlley down and carries a weight of 800 N at its end.
μ = 0.2. Determine:
A) Tension in the rope
B) Acceleration with which the body moves up the plane and
C) The distance moved by the body in 3 sec after starting from rest.
Q6) Two bodies of weights 40 N and 15 N are connected to the two ends of a light inextensible
string which passes over a smooth pulley. The weight 40 N is placed on a smooth inclined plane
while the weight 15 N is hanging free in air. If the angle of the plane is 150
determine
a) Acceleration of the system and
b) Tension in the string ( May 2002 8 Mks)

6. D’Alembert’s Principle Page 6
Q7) A body weighing 300 N on a horizontal table 1.2 m from the edge is attached by a string to a
30 N weight which hangs over the edge. The co-efficient of friction between the 300 N body and
table is
1
16
. Find the acceleration of the system and the time required for the 300 N body to fall
over the edge. (May 2007 12 Mks)
Q8) A block weighing 1 kN on a horizontal plane as showing in Figure below. Find the
magnitude of the force P required to give the block an acceleration of 3 m/s2
to the right. Take μ
= 0.25.

7. D’Alembert’s Principle Page 7
Type III) Analysis of Lift Motion:
Q1) A man weighing ‘W’ N exerted a lift which moves with an acceleration of ‘a’ m/s2
. Find the
force exerted by the man on the floor of lift when
a) Lift is moving downward
b) Lift is moving upward
Q2) A elevator cage of a mine shaft weighing 8 kN when empty, is lifted or lowered by means of
a wire rope. Once a man weighing 600 N, entered it and lowered with uniform acceleration such
that, when a distance of 187.5 m was covered, the velocity of the cage was 25 m/s. determine the
tension in the rope and the force exerted by the man on the floor of the cage.
Q3) An elevator of weight 4.5 kN starts to move upwards with a constant acceleration and
acquires a velocity of 1.8 m/s after travelling a distance of 2.4 m. Find the pull in the cable
during accelerated motion. The elevator moves further with constant deceleration from a velocity
of 1.8 m/s and comes to rest in 2 sec. Calculate the pressure exerted by a man weighing 680 N on
the floor of the elevator during this motion. (Dec 2008 13 mks)
Q4) A 750 N crate rests on a 500 N cart. The co-efficient of friction between the crate and the
cart is 0.3 and between cart and the road is 0.2. if the cart is to be pulled by a force P (as shown
in Figure below) such that the crate does not slip, determine
a) The maximum allowable magnitude of P and
b) The corresponding acceleration of the cart.

8. D’Alembert’s Principle Page 8
Q5) A force of 200 N acts on a body having mass of 300 kg for 90 sec. If the initial velocity
of the body is 20 m/s, determine the final velocity of the body
a) When the force acts in the direction of motion, and
b) When the force acts in the opposite direction of the motion
Q6) A man weighing 637 N dives into a swimming pool from a tower of height 19.6 m. He
was found to go down in water by 2 m and then started rising. Find the average resistance of
water. Neglect the resistance of air.
Q7) A man mass 60 kg jumps into a swimming pool from a tower of height 6 m. He was
found to go down in water by 0.9 m and then started rising. Find the average resistance of
water. Neglect the resistance of air. (8 Mks)