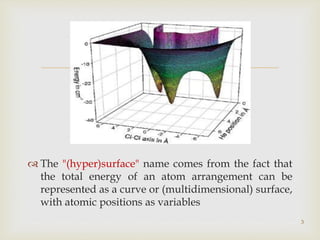
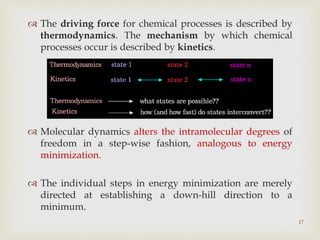
The document discusses the conformation and potential energy of molecules, highlighting different methodologies for calculating these energies, including molecular mechanics and quantum mechanics. It emphasizes the role of molecular dynamics in simulating molecular interactions and the importance of energy minimization to identify local energy minima within a biomolecule's energy landscape. Additionally, it addresses the computational aspects and challenges associated with molecular dynamics simulations and the factors guiding molecular movement.

1. By
Mr.Bhavesh B.Amrute
( M.Pharm, Pharmaceutical Chemistry )
1

2. 
 All molecules have a range of conformation produced
by vibrations of all the bonds and the torsional rotations
about the single bonds.
 Potential energy of the molecule is directly proportional
to its conformation.
 Denoted by PES (Potential energy Surface).
Introduction
2

3. 
 The "(hyper)surface" name comes from the fact that
the total energy of an atom arrangement can be
represented as a curve or (multidimensional) surface,
with atomic positions as variables
.
3

4. 
 There are various methodologies to calculate
Potential Energy of the different types of molecules.
 Molecular Mechanics (MM)
 Quantum Mechanics (QM)
How to calculate Potential Energy?
4

5. 
 Small molecular structure can be minimized using ab
initio or semi-empirical quantum mechanics (using
programs such as Spartan).
 Large molecular structures (like DNA, RNA,
proteins and their complexes) must be minimized
using molecular mechanics, based on Newton's
laws.
Quantum Mechanics Vs Molecular Mechanics
5

6. 
 Molecular dynamics (MD) is a computer simulation
of physical movements of atoms and molecules.
 The atoms and molecules are allowed to interact for
a period of time, giving a view of the motion of the
atoms.
 The goal of molecular dynamics is to simulate the
actual changes in a molecule as a function of time
after an energy input (heat application at a higher
temperature) is added to a molecule at equilibrium.
Then what is Molecular Dynamics?
6

7. 
Particular Role
Molecular Mechanics Energy minimization of larger molecules
Quantum Mechanics Energy minimization of smaller molecules
Molecular Dynamics To study the interaction of small-large
and/or large-large molecules by
simulation
Whose Role is What?
7

8. 
 Function optimization is a calculation that pervades
much of numerical analysis.
 In the context of macromolecules, the function to be
optimized (minimized) is an energy.
 The energy landscape of a biomolecule possesses an
enormous number of minima, or conformational
substates.
Energy Minimization
aka Energy Optimization aka Geometry
Optimization
8

9. 
 Nonetheless, the goal of energy minimization is
simply to find the local energy minimum.
 The energy at this local minimum may be much
higher than the energy of the global minimum.
 Physically, energy minimization corresponds to an
instantaneous freezing of the system; a static
structure in which no atom feels a net force
corresponds to a temperature of 0 K.
9

10. 
 Very briefly, a force field is a mathematical function
which returns the energy of a system as a function of the
conformation of the system.
 The "mechanical" molecular model was developed out of
a need to describe molecular structures and properties in
as practical manner as possible.
 The range of applicability of molecular mechanics
includes:
 Molecules containing thousands of atoms.
 Organics, oligonucleotides, peptides, and saccharides
(metallo-organics and inorganics in some cases).
 Thermodynamic and kinetic (via molecular dynamics)
properties.
Force Field aka Molecular
Mechanics
10

11. 

11

12. 

12

13. 
 The great computational speed of molecular mechanics
allows for its use in procedures such as molecular
dynamics, conformational energy searching, and docking.
All the procedures require large numbers of energy
evaluations.
 Molecular mechanics methods are based on the following
principles:
 Nuclei and electrons are lumped into atom-like particles.
 Atom-like particles are spherical (radii obtained from
measurements or theory) and have a net charge (obtained
from theory).
 Interactions are based on springs and classical potentials.
 Interactions must be preassigned to specific sets of atoms.
 Interactions determine the spatial distribution of atom-like
particles and their energies.
13

14. 
 The goal of molecular dynamics is to simulate the actual
changes in a molecule as a function of time after an energy
input (heat application at a higher temperature) is added to a
molecule at equilibrium.
 To make the simulation realistic, the structure is placed in a
"bath" of thousands of water molecules.
 In the most common version, the trajectories of molecules and
atoms are determined by numerically solving the Newton's
equations of motion for a system of interacting particles, where
forces between the particles and potential energy are defined by
molecular mechanics force fields.
Molecular Dynamics (MD)
14

15. 15
 Because molecular systems consist of a vast number
of particles, it is impossible to find the properties of
such complex systems analytically; MD simulation
circumvents this problem by using numerical
methods.
 However, long MD simulations are mathematically
ill-conditioned, generating cumulative errors in
numerical integration that can be minimized with
proper selection of algorithms and parameters, but
not eliminated entirely.

16. 16
 In the broadest sense, molecular dynamics is
concerned with molecular motion. Motion is
inherent to all chemical processes.
 Simple vibrations, like bond stretching and angle
bending, give rise to IR spectra.
 Chemical reactions, hormone-receptor binding, and
other complex processes are associated with many
kinds of intra- and intermolecular motions.

17. 17
 The driving force for chemical processes is described by
thermodynamics. The mechanism by which chemical
processes occur is described by kinetics.
 Molecular dynamics alters the intramolecular degrees of
freedom in a step-wise fashion, analogous to energy
minimization.
 The individual steps in energy minimization are merely
directed at establishing a down-hill direction to a
minimum.

18. 
 The rate and direction of motion (velocity) are governed by the
forces that the atoms of the system exert on each other as
described by Newton's equation.
 In practice, the atoms are assigned initial velocities that
conform to the total kinetic energy of the system, which in turn,
is dictated by the desired simulation temperature.
 The basic ingredients of molecular dynamics are the calculation
of the force on each atom, and from that information, the
position of each atom throughout a specified period of time
(typically on the order of picoseconds = 10^-12 seconds).
Newton’s Equation in MD
18

19. 19
 Energies can be calculated using either molecular mechanics or
quantum mechanics methods.
 Molecular mechanics energies are limited to applications that
do not involve drastic changes in electronic structure such as
bond making/breaking.
 Quantum mechanical energies can be used to study dynamic
processes involving chemical changes.