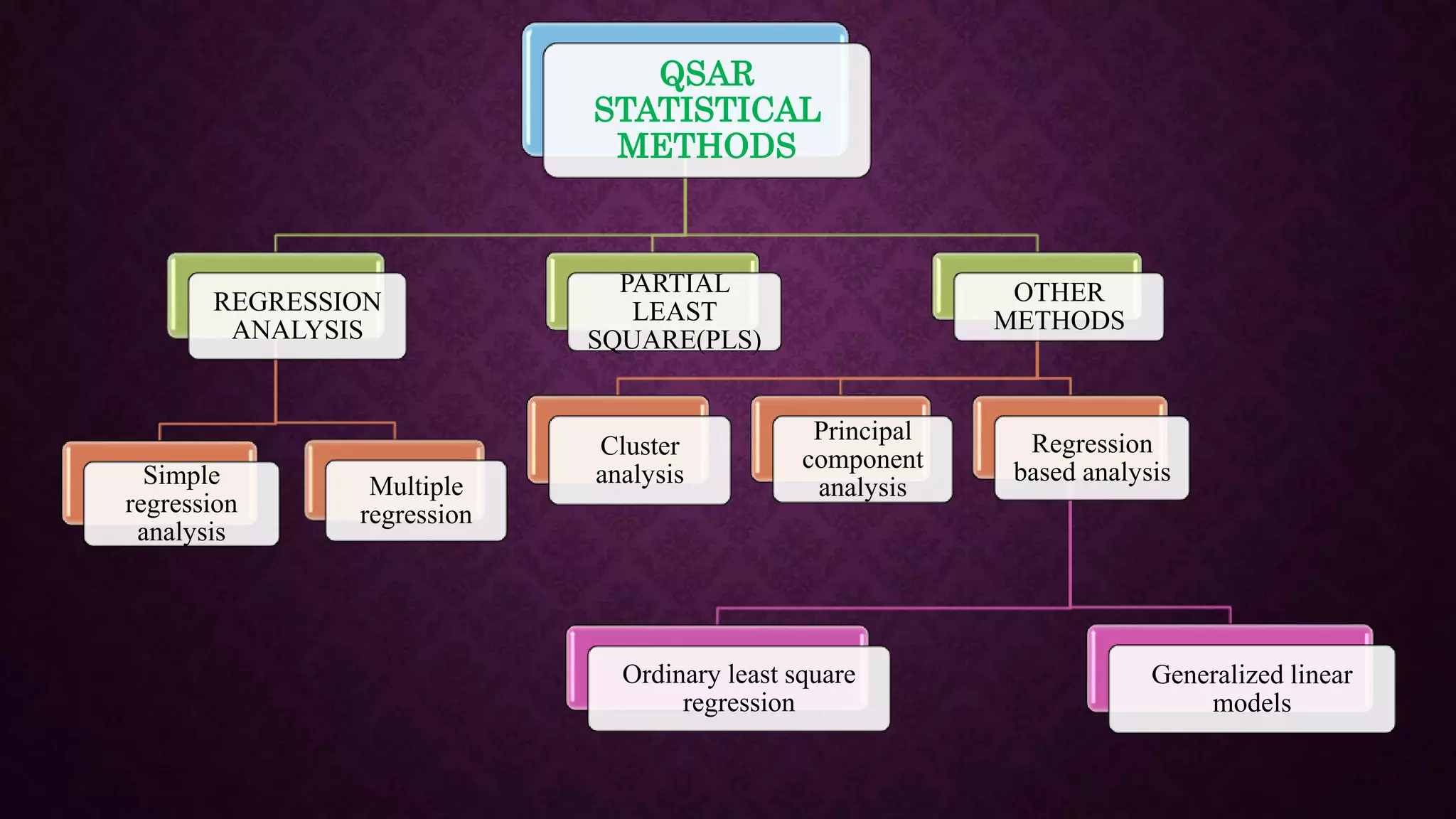
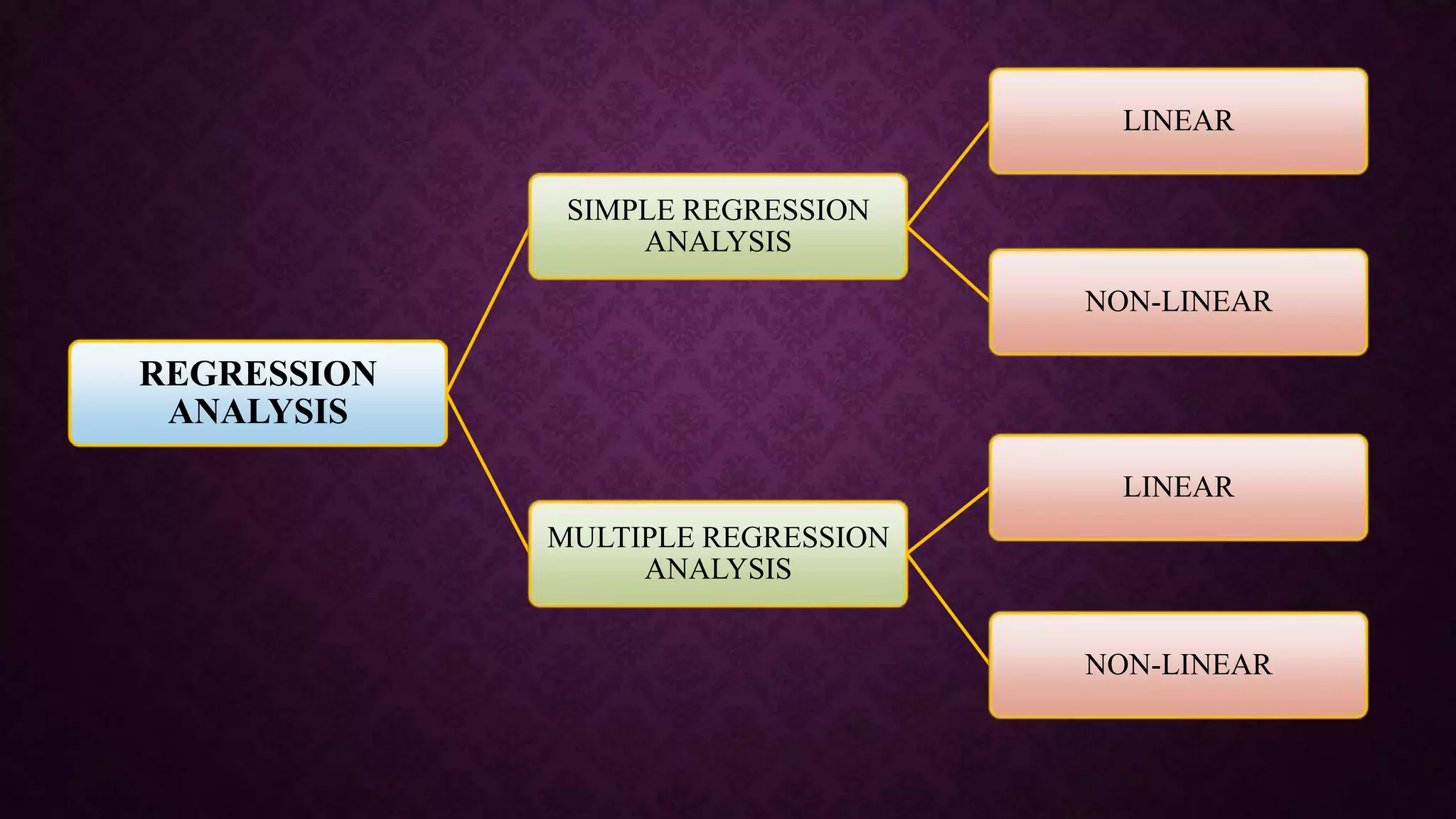
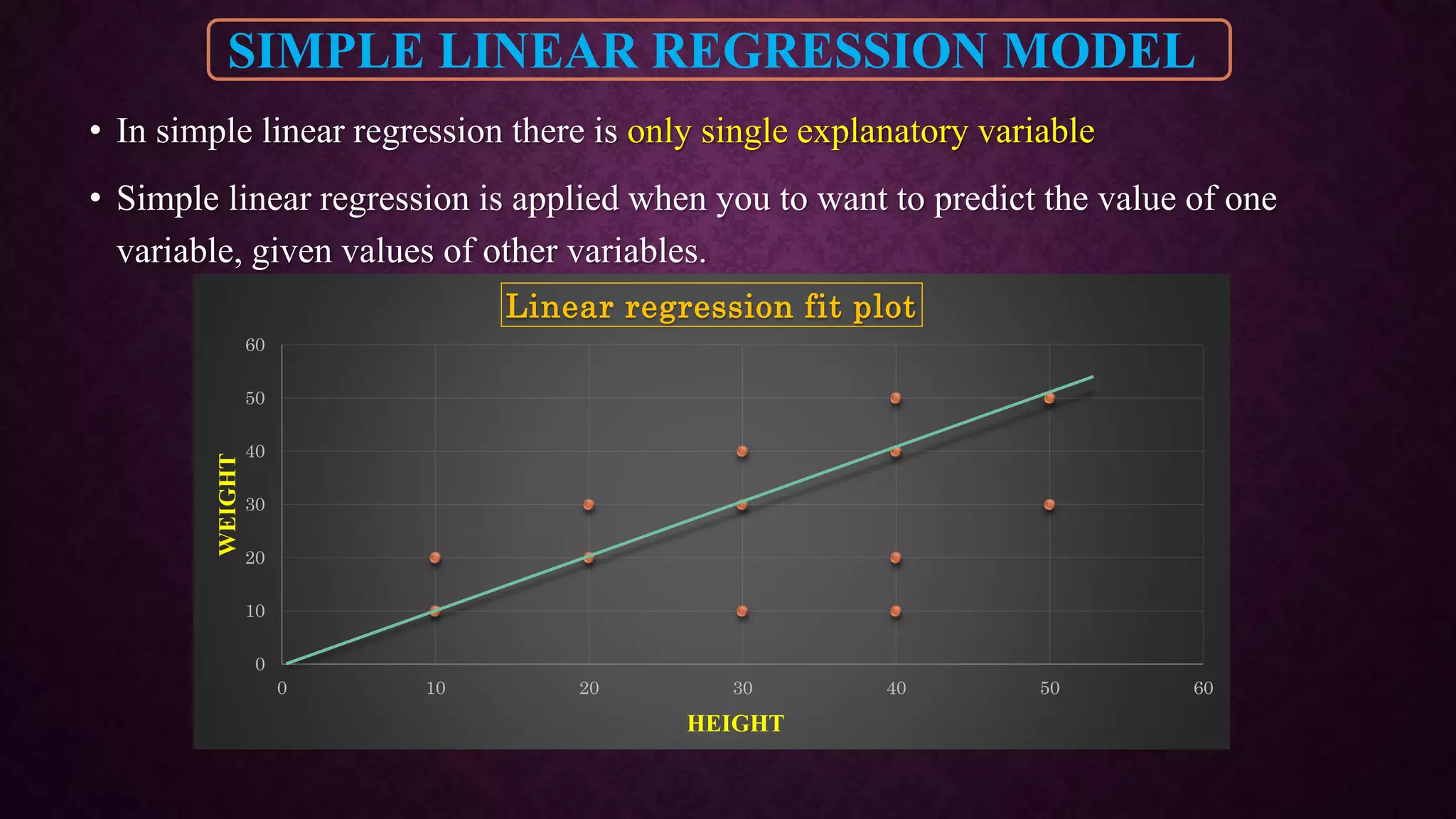
The document provides an overview of quantitative structure-activity relationship (QSAR) and its statistical methods, including regression analysis and partial least squares (PLS). It outlines various regression techniques, their applications, and the significance of statistical modeling in establishing relationships among variables in pharmacology and chemistry. Additional methods discussed include cluster analysis and principal component analysis, emphasizing their roles and applications across different fields.

1. QSAR STATISTICAL
METHODS
PRESENTED BY-GAYATRI SATI
CLASS-M.PHARMA-2nd sem
(PHARMACOLOGY)

2. TABLE OF CONTENTS
1. INTRODUCTION OF QSAR
2. QSAR STATISTICAL METHODS
3. REGRESSION ANALYSIS
4. APPLICATION OF REGRESSION ANALYSIS
5. PARTIAL LEAST SQUARE ANALYSIS
6. APLICATION OF PLS
7. OTHER METHODS
8. REFERENCES

3. INTRODUCTION OF QSAR
• Quantitative structure activity relationship (QSAR) is a strategy of the essential
importance for chemistry and pharmacy, based on the idea that when we change a
structure of a molecule then also the activity or property of the substance will be
modified.
• QSAR are mathematical relationships between the physicochemical properties and
pharmacological/biological activity in a quantitative manner for a series of compound.
Biological activity=f (physicochemical properties and /or structure properties)
• Statistics is a branch of mathematics dealing with data collection, organization, analysis,
interpretation and presentation

5. QSAR
STATISTICAL
METHODS
REGRESSION
ANALYSIS
Simple
regression
analysis
Multiple
regression
PARTIAL
LEAST
SQUARE(PLS)
OTHER
METHODS
Cluster
analysis
Principal
component
analysis
Regression
based analysis
Ordinary least square
regression
Generalized linear
models

6. INDTRODUCTION REGRESSION ANALYSIS
• In statistical modeling, regression analysis is a set of statistical processes for
estimating the relationships among variables.
• Regression analysis correlates independent X variables with dependent Y variables.
• If two variables are involved, the variable that is basis of estimation is called the
independent variable and the variable whose value is to be estimated is called as
dependent variable.
• For any given values of X, the Y values are independent and follow a normal
distribution curve.

7. DEFINITION OF REGRESSION ANALYSIS
Regression analysis is a technique of studying the dependence of one variable (called
dependent Y variable e.g. biological data) on one or more variables (called independent X
variable e.g. physicochemical parameters) with a view to estimate or predict the average
value of dependent variable in terms of known or fixed values of the independent variable.
The dependent variable is also called as-
»Explained »Response »Endogenous
The independent variable is also called as-
»Explanatory »Regressor »Exogenous

8. REGRESSION MODELS
• Regression models involve the following parameters and variables. The unknown
parameter known as β, which may be a scalar or vector
• A regression model relates Y to a function of X and β
Y ≈ f (X, β)
where;
f = function
β = unknown parameter
X=independent variable
Y=dependent variable

9. Assume now that the vector of unknown parameters β is of length K, In order to
perform a regression analysis the user must provide information about the dependent
variable Y
 If N data points of the form (Y, X) are observed, where N < K, most classical
approaches to regression analysis cannot be performed.
If N = K data points are observed, and the function f is linear, the equations Y ≈ f (X,
β) can be solved exactly rather than approximately.
If N > K data points are observed, there is enough information in the data to estimate
the unique value for β.

10. REGRESSION
ANALYSIS
SIMPLE REGRESSION
ANALYSIS
LINEAR
NON-LINEAR
MULTIPLE REGRESSION
ANALYSIS
LINEAR
NON-LINEAR

11. SIMPLE LINEAR REGRESSION MODEL
• In simple linear regression there is only single explanatory variable
• Simple linear regression is applied when you to want to predict the value of one
variable, given values of other variables.
0
10
20
30
40
50
60
0 10 20 30 40 50 60
WEIGHT
HEIGHT
Linear regression fit plot

12. SIMPLE LINEAR REGRESSION
Simple linear regression for a derivation of these formulas
Yᵢ = β̥+ β1 Xᵢ + εᵢ
Where,
Yᵢ=Dependent variable
β̥=Population Y intercept
β1= Population slope coefficient linear component
Xᵢ=Independent variable
εᵢ=Random error term Random error component

13. MULTIPLE LINEAR REGRESSION
• Multiple linear regression is the same idea as simple linear regression, except how you
have several independent variables predicting the dependent variables
• It is used when we want to predict the value of a variable based on the value of two or
more other variables
Y=β ̥+ β1X1 + β2 X2 +……….+ βn Xn + ε
Where,
N=number of variable
β̥=intercept term
βn=Coefficients for independent variable
β= unknown parameter

14. USES OF REGRESSION ANALYSIS
1. Regression analysis helps in establishing the relationship between two or more
variables
2. Regression analysis predicts the value of dependent variables from the values of
independent variables
3. Coefficient of correlation and coefficient of determination can be calculated with the
help of regression analysis
4. Regression analysis is widely used as statistical tool in QSAR.

15. PARTIAL LEAST SQUARE ANALYSIS(PLS)
• Partial least square analysis (PLS) is a method for constructing predictive models when
the factors are many and collinear
• It is a recent technique that generalizes and combines features from principal
component analysis and multiple regression
• Goal-predict set of dependent variables Y from a set of independent variables X
describe their common structure
• Used to Find the fundamental relations between the two variables/matrices (X and Y)
• COMPACT (computer optimized molecular parametric analysis of chemical toxicity),
a PLS approach, is described to predict carcinogenicity and other forms of toxicity.

16. SOFTWARES USED IN PLS
Its application depends on the availability of software
• SIMCA-P
• UNSCRAMBLER
• SPM
• SAS PROC PLS

17. APPLICATIONS OF PLS
• PLS is used to find the fundamental relations between two matrices (X and Y)
• PLS model will try to find the maximum multidirectional direction in the X space
and the maximum multidimensional direction in the Y space
• PLS regression is widely used in chemo metrics especially in the case where the
number of independent variables is significantly larger than the number of data
points and related areas
• It is also used in bioinformatics, sensometrics, neuroscience and anthropology.

18. OTHER MULTIVARIABLE STATISTICAL MODELS
1. Cluster analysis
2. Principal component analysis
3. Regression based analysis methods
a) Ordinary least square regression
b) Generalized linear models

19. 1. CLUSTER ANALYSIS
• Cluster analysis is a group of multivariate techniques whose primary purpose is to group
objects based on the characteristics they possess.
• In cluster analysis, the grouping is based on the distance (proximity)
• It is the main task of exploratory data mining, statistical data analysis, pattern
recognition, image analysis, bioinformatics, data compression and computer graphics

20. ROLE &APPLICATIONS OF CLUSTER ANALYSIS
ROLES-
1. Data reduction
2. Hypotheses generation
APPLICATIONS-
1. Medicine
2. Analysis of antimicrobial activity
3. Biology & bioinformatics
4. Field of psychiatry
5. Climate
6. Sequence analysis
7. Crime analysis & transcriptomic

21. 2. PRINCIPAL COMPONENT ANALYSIS
• It is a exploratory technique used to reduce the dimensionality of data set to 2D or 3D
• PCA is a procedure that transforms a number of possibly correlated variables into a
smaller number of uncorrelated variables called principal components
• Objective of PCA:-
PCA is a dimensionality reduction or data compression method
• Goal of PCA:-
To select a subset of variables from a larger set, based on which original variables have
the highest correlations with the principal component

22. APPLICATIONS OF PCA
1. Neuroscience: A variant of PCA is used in neuroscience to identify the specific
properties of a stimulus that increase a neuron’s probability of generating an action
potential. This technique is known as spike triggered covariance analysis. In
neuroscience, PCA is also used to discern the identify of a neuron from the shape of
its action potential.
2. Quantitative finance: PCA can be directly applied to the risk management of interest
rate derivatives portfolios.

23. 3. REGRESSION BASED ANALYSIS
a) Ordinary least squares:-
• In statistics, ordinary least squares (OLS) is a type of linear least squares
method for estimating the unknown parameters in a linear regression model.
• OLS is used in fields as diverse as economics (econometrics), data science,
political science, psychology and engineering (control theory and signal
processing)
b) Generalized linear model:-
• In statistics, the generalized linear model (GLM) is a flexible generalization
of ordinary linear regression that allows for response variables that have error
distribution models other than a normal distribution.

24. REFERENCES
1. https://en.wikipedia.org/wiki/Statistics
2. www.statstutor.ac.uk/resources/uploaded/1introduction3.pdf
3. http://home.iitk.ac.in/~kundu/Statistical
4. Methods.pdfhttps://en.wikipedia.org/wiki/Regression_analysis#Linear_regression

25. ”NEVER TRUST A STATISTICS YOU DIDN’T FORGE YOURSELF ”
-WINSTON CHURCHILL