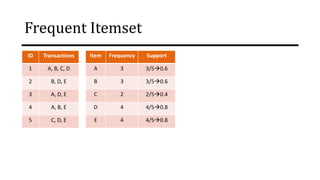
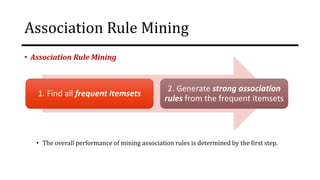
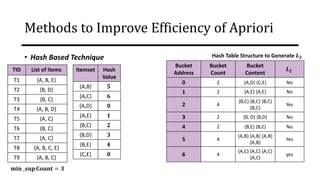
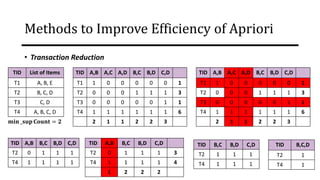
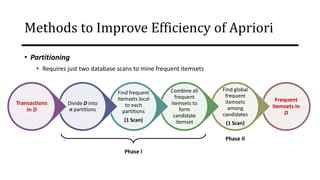
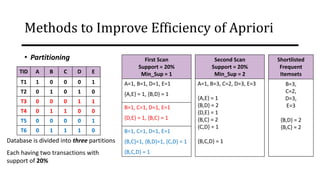
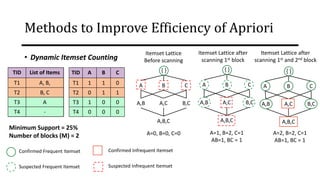
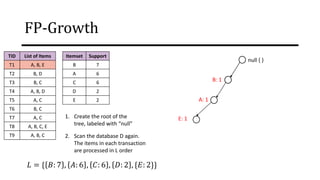
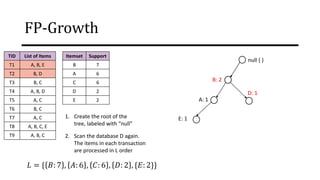
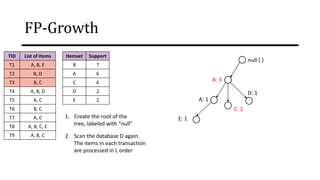
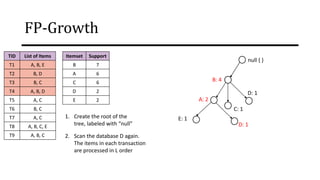
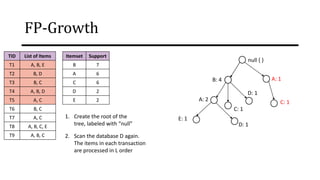
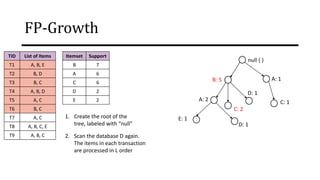
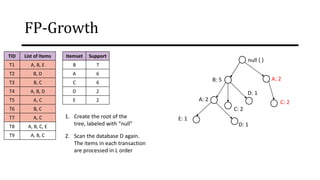
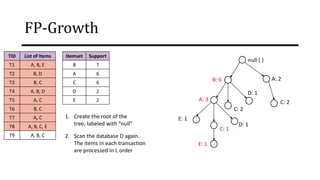
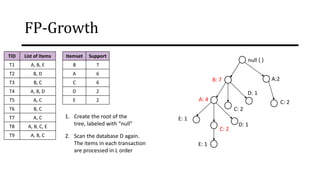
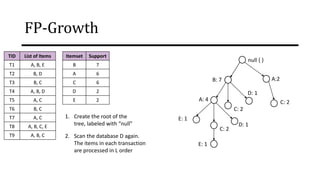
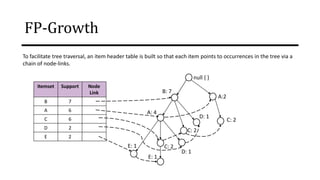
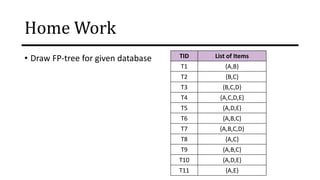
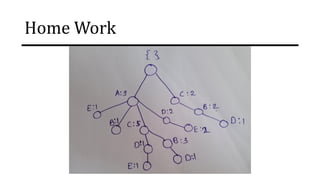
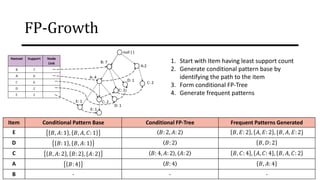
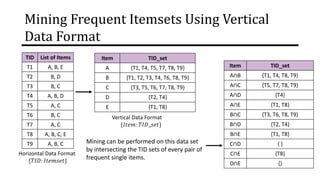
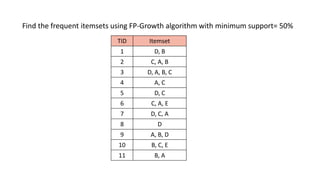
The document discusses frequent pattern mining and association rule mining. It defines key concepts like frequent itemsets, association rules, support and confidence. It explains the Apriori algorithm for mining frequent itemsets in multiple steps. The algorithm uses a level-wise search approach and the Apriori property to reduce the search space. It generates candidate itemsets in the join step and determines frequent itemsets by pruning infrequent candidates in the prune step. An example applying the Apriori algorithm to a retail transaction database is also provided to illustrate the working of the algorithm.

1. Ms. Rashmi Bhat
Mining Frequent
Patterns And
Association
Rules

2. Does This Look
Familiar???

3. What is a Frequent Pattern?
• A frequent pattern is a pattern that appears in a data set frequently.
• What are these frequent patterns?
Frequent Itemsets

4. What is a Frequent Pattern?
• A frequent pattern is a pattern that appears in a data set frequently.
• What are these frequent patterns?
• Frequent Itemsets
• Frequent Sequential Pattern
• Frequent Structured Patterns etc
• Searching for recurring relationships in a given data set.
• Discovering interesting associations and correlations
between itemsets in transactional databases.
What is Frequent Pattern Mining?

5. Market Basket Analysis

6. Market Basket Analysis
• Analyzes customer buying habits by finding associations between the different
items that customers place in their “shopping baskets”.
• How does this help retailers?
• Helps to develop marketing strategies by gaining insight into which items are frequently
purchased together by customers.

7. Market Basket Analysis
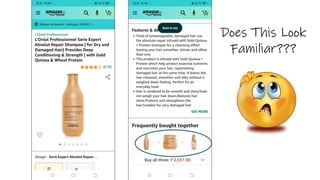
• Buying patterns which reflect items frequently purchased or associated together
can be represented in rules form, known as association rules.
• e.g.
{𝑴𝒐𝒃𝒊𝒍𝒆} ⇒ 𝑺𝒄𝒓𝒆𝒆𝒏𝑮𝒖𝒂𝒓𝒅, 𝑩𝒂𝒄𝒌𝒄𝒐𝒗𝒆𝒓 [𝑠𝑢𝑝𝑝𝑜𝑟𝑡 = 5%, 𝑐𝑜𝑛𝑓𝑖𝑑𝑒𝑛𝑐𝑒 = 65%]
• Interestingness measures: 𝑺𝒖𝒑𝒑𝒐𝒓𝒕 and 𝑪𝒐𝒏𝒇𝒊𝒅𝒆𝒏𝒄𝒆
• Reflect the usefulness and certainty of discovered rules.
• Association rules are considered interesting if they satisfy both a minimum support
threshold and a minimum confidence threshold.
• Thresholds can be set by users or domain experts.

8. Association Rule
Let
𝑰 = 𝑷𝒆𝒏, 𝑷𝒆𝒏𝒄𝒊𝒍, 𝑬𝒓𝒂𝒔𝒆𝒓, 𝑵𝒐𝒕𝒆𝒃𝒐𝒐𝒌, 𝑹𝒖𝒍𝒆𝒓, 𝑴𝒂𝒓𝒌𝒆𝒓, 𝑺𝒄𝒊𝒔𝒔𝒐𝒓𝒔, 𝑮𝒍𝒖𝒆 … …Set of items in shop
𝑫 is task relevant dataset
𝑻 = 𝑷𝒆𝒏𝒄𝒊𝒍, 𝑷𝒆𝒏, 𝑵𝒐𝒕𝒆𝒃𝒐𝒐𝒌, 𝑬𝒓𝒂𝒔𝒆𝒓 , 𝑻 ⊂ 𝑰 …Transaction
𝑨 = 𝑷𝒆𝒏, 𝑷𝒆𝒏𝒄𝒊𝒍, 𝑵𝒐𝒕𝒆𝒃𝒐𝒐𝒌, 𝑺𝒄𝒊𝒔𝒔𝒐𝒓𝒔 , 𝑩 = 𝑬𝒓𝒂𝒔𝒆𝒓, 𝑮𝒍𝒖𝒆 … Set of items
𝑨 ⇒ 𝑩
An Association Rule … 𝑤ℎ𝑒𝑟𝑒 𝐴 ⊂ 𝐼, 𝐵 ⊂ 𝐼 𝑎𝑛𝑑 𝐴 ∩ 𝐵 = ∅
An Association Rule 𝑨 ⇒ 𝑩 holds in transaction set with support 𝒔 and confidence 𝒄

9. Association Rule
Support s, where s is the percentage of transactions in D that contain 𝑨 ∪ 𝑩
Confidence c, where c is the the percentage of transactions in D
containing 𝑨 that also contain 𝐵.
𝑺𝒖𝒑𝒑𝒐𝒓𝒕 𝑨 ⇒ 𝑩 = 𝑷(𝑨 ∪ 𝑩)
𝑪𝒐𝒏𝒇𝒊𝒅𝒆𝒏𝒄𝒆 𝑨 ⇒ 𝑩 = 𝑷(𝑩|𝑨)
Rules that satisfy both a minimum support threshold (min_sup) and a minimum
confidence threshold (min_conf) are called strong rules.

10. Some Important Terminologies
• Itemset is a set of items.
• An itemset that contains k items is a k-itemset.
• The occurrence frequency of an itemset is the number of transactions that contain the
itemset. This is also known as the frequency, support count, or count of the itemset.
• The occurrence frequency is called the absolute support.
• If an itemset 𝐼 satisfies a prespecified minimum support threshold, then 𝐼 is a frequent
itemset
• The set of frequent 𝑘-itemsets is commonly denoted by 𝐿𝑘
𝒄𝒐𝒏𝒇𝒊𝒅𝒆𝒏𝒄𝒆 𝑨 ⇒ 𝑩 =
𝒔𝒖𝒑𝒑𝒐𝒓𝒕(𝑨 ∪ 𝑩)
𝑺𝒖𝒑𝒑𝒐𝒓𝒕(𝑨)
=
𝒔𝒖𝒑𝒑𝒐𝒓𝒕_𝒄𝒐𝒖𝒏𝒕(𝑨 ∪ 𝑩)
𝒔𝒖𝒑𝒑𝒐𝒓𝒕_𝒄𝒐𝒖𝒏𝒕(𝑨)

11. Frequent Itemset
ID Transactions
1 A, B, C, D
2 B, D, E
3 A, D, E
4 A, B, E
5 C, D, E
Item Frequency
A 3
B 3
C 2
D 4
E 4
Item Frequency Support
A 3 3/5→0.6
B 3 3/5→0.6
C 2 2/5→0.4
D 4 4/5→0.8
E 4 4/5→0.8

12. Association Rule Mining
• Association Rule Mining
• The overall performance of mining association rules is determined by the first step.
1. Find all frequent Itemsets
2. Generate strong association
rules from the frequent itemsets

13. Itemsets
• Closed Itemset
• An itemset 𝑋 is closed in a data set 𝑆 if there exists no proper super-itemset 𝑌 such that 𝑌
has the same support count as 𝑋 in 𝑆.
• If 𝑋 is both closed and frequent in 𝑆, then 𝑋 is a closed frequent itemset in 𝑆.
• Maximal Itemset
• An itemset 𝑋 is a maximal frequent itemset (or max-itemset) in set 𝑆, if 𝑋 is frequent,
and there exists no super-itemset 𝑌 such that 𝑋 ⊂ 𝑌 and 𝑌 is frequent in 𝑆.

14. Closed and Maximal Itemsets
• Frequent itemset 𝑋 ∈ 𝐹 is maximal if it does not have any frequent
supersets
• That is, for all 𝑋 ⊂ 𝑌, 𝑌 ∉ 𝐹
• Frequent itemset 𝑋 ∈ 𝐹 is closed if it has no immediate superset with
the same frequency
• That is, for all 𝑋 ⊂ 𝑌, 𝑠𝑢𝑝𝑝𝑜𝑟𝑡 𝑌, 𝐷 < 𝑠𝑢𝑝𝑝𝑜𝑟𝑡(𝑋, 𝐷)

15. TID Itemset
1 {A, C, D}
2 {B, C, D}
3 {A, B, C, D}
4 {B, D}
5 {A, B, C, D}
min_sup = 3
i.e. min_sup = 60%
null
A B C D
A,B A,C A,D B,C B,D C,D
A,B,C A,B,D A,C,D B,C,D
A,B,C,D
3 4 4 5
2
3 3 3 4 4
2 2 3 3
2
1- Item set
2-Item set
3-Item set
4-Item set
A B C D
A,B A,C A,D B,C

16. TID Itemset
1 {A, C, D}
2 {B, C, D}
3 {A, B, C, D}
4 {B, D}
5 {A, B, C, D}
min_sup = 3
i.e. min_sup = 60%
null
A B C D
A,B A,C A,D B,C B,D C,D
A,B,C A,B,D A,C,D B,C,D
A,B,C,D
3 4 4 5
2
3 3 3 4 4
2 2 3 3
2
Frequent Itemset Infrequent Itemset
1- Item set
2-Item set
3-Item set
4-frequent Item set

17. TID Itemset
1 {A, C, D}
2 {B, C, D}
3 {A, B, C, D}
4 {B, D}
5 {A, B, C, D}
min_sup = 3
i.e. min_sup = 60%
null
A B C D
A,B A,C A,D B,C B,D C,D
A,B,C A,B,D A,C,D B,C,D
A,B,C,D
3 4 4 5
2
3 3 3 4 4
2 2 3 3
2
Frequent Itemset Infrequent Itemset
D 1- Item set
2-Item set
3- Item set
4-Item set
Closed Frequent Itemset
B,D C,D
(but not maximal)

18. TID Itemset
1 {A, C, D}
2 {B, C, D}
3 {A, B, C, D}
4 {B, D}
5 {A, B, C, D}
min_sup = 3
i.e. min_sup = 60%
null
A B C D
A,B A,C A,D B,C B,D C,D
A,B,C A,B,D A,C,D B,C,D
A,B,C,D
3 4 4 5
2
3 3 3 4 4
2 2 3 3
2
Frequent Itemset Infrequent Itemset
D 1- Item set
2-Item set
3- Item set
4- Item set
Closed Frequent Itemset
B,D C,D
Maximal Frequent Itemset
A,C,D B,C,D
(but not maximal)

19. Frequent Pattern Mining
• Frequent pattern mining can be classified in various ways as follows:
Based on the completeness of patterns to be mined
Based on the levels of abstraction involved in the rule set
Based on the number of data dimensions involved in the rule
Based on the types of values handled in the rule
Based on the kinds of rules to be mined
Based on the kinds of patterns to be mined

20. Frequent Pattern Mining
• Based on the completeness of the patterns to be mined
• The complete set of frequent itemsets,
• The closed frequent itemsets, and the maximal frequent itemsets
• The constrained frequent itemsets
• The approximate frequent itemsets
• The near-match frequent itemsets
• The top-k frequent itemsets

21. Frequent Pattern Mining
• Based on the levels of abstraction involved in the rule set
• We can find rules at differing levels of abstraction
• multilevel association rules
• Based on the number of data dimensions involved in the rule
• Single-dimensional association rule
• Multidimensional association rule
• Based on the types of values handled in the rule
• Boolean association rule
• Quantitative association rule

22. Frequent Pattern Mining
• Based on the kinds of rules to be mined
• Association rules
• Correlation rules
• Based on the kinds of patterns to be mined
• Frequent itemset mining
• Sequential pattern mining
• Structured pattern mining

23. Efficient and Scalable Frequent Itemset
Mining Methods
• Methods for mining the simplest form of frequent patterns
• Single-dimensional,
• Single-level,
• Boolean frequent itemsets
• Apriori Algorithm
• basic algorithm for finding frequent itemsets
• How to generate strong association rules from frequent itemsets?
• Variations to the Apriori algorithm

24. Apriori Algorithm
• Finds Frequent Itemsets Using Candidate Generation
• The algorithm uses prior knowledge of frequent itemset properties
• Employs an iterative approach known as a level-wise search
• k-itemsets are used to explore (k+1)-itemsets
• Apriori property, is used to reduce the search space.
• If a set cannot pass a test, all of its supersets will fail the same test as well.
Apriori property: All nonempty subsets of a frequent itemset must also be frequent.

25. Apriori Algorithm
• Apriori algorithm follows a two step process
• Join Step:
• To find 𝐿𝑘, a set of candidate 𝑘-itemsets is generated by joning 𝐿𝑘−1 with itself.
• This set of candidates is denoted 𝐶𝑘
• Prune Step:
• 𝐶𝑘 is a superset of 𝐿𝑘, that is, its members may or may not be frequent, but all of the
frequent 𝑘-itemsets are included in 𝐶𝑘.
• A scan of the database to determine the count of each candidate in 𝐶𝑘 would result in the
determination of 𝐿𝑘.
• To reduce the size of 𝐶𝑘, the Apriori property is used
• Any (𝑘 − 1)-itemset that is not frequent cannot be a subset of a frequent 𝑘-itemset.
Prune
Step
Join
Step

26. Apriori Algorithm
Transactional data for a retail shop
• Find the frequent itemsets using Apriori algorithm
• There are eight transactions in this database, that is,
𝐷 = 8.
T_id List of Item
1 { Milk, Eggs, Bread, Butter }
2 {Milk, Bread }
3 { Eggs, Bread, Butter }
4 {Milk, Bread, Butter }
5 { Milk, Bread, Cheese }
6 { Eggs, Bread, Cheese }
7 { Milk, Bread, Butter, Cheese}
8 { Milk, Eggs, }

27. Apriori Algorithm
Iteration 1:
• Generate candidate itemset 𝐶1 (1-itemset)
• Suppose that the minimum support count required is 3, i.e ,
𝒎𝒊𝒏 _𝒔𝒖𝒑=𝟑 (relative support is 3/8=37.5%)
Item
{ Milk }
{ Eggs }
{ Bread }
{ Butter }
{ Cheese }
T_id List of Item
1 { Milk, Eggs, Bread, Butter }
2 {Milk, Bread }
3 { Eggs, Bread, Butter }
4 {Milk, Bread, Butter }
5 { Milk, Bread, Cheese }
6 { Eggs, Bread, Cheese }
7 { Milk, Bread, Butter, Cheese}
8 { Milk, Eggs, }
Support
Count
6
4
7
4
3
𝑪𝟏

28. Apriori Algorithm
Iteration 1:
• Generate candidate itemset 𝐶1
• Suppose that the minimum support
count required is 3, i.e , 𝒎𝒊𝒏 _𝒔𝒖𝒑=𝟑
(relative support is 3/8=37.5%)
• The set of frequent 1-itemsets, 𝑳𝟏,
can then be determined.
• Prune Step: Remove all the itemsets
not satisfying minimum support.
• 𝐿1 consists Candidate 1-itemsets
satisfying minimum support.
Frequent 1-Itemset 𝑳𝟏
Item Support
{ Milk } 6
{ Eggs } 4
{ Bread } 7
{ Butter } 4
{ Cheese } 3
T_id List of Item
1 { Milk, Eggs, Bread, Butter }
2 {Milk, Bread }
3 { Eggs, Bread, Butter }
4 {Milk, Bread, Butter }
5 { Milk, Bread, Cheese }
6 { Eggs, Bread, Cheese }
7 { Milk, Bread, Butter, Cheese}
8 { Milk, Eggs, }

29. Apriori Algorithm
Iteration 2:
• Join Step: Join 𝐿1 × 𝐿1 to generate candidate itemset 𝐶2
𝑪𝟐
Item
{ Milk, Eggs }
{ Milk, Bread }
{ Milk, Butter }
{ Milk, Cheese }
{ Eggs, Bread}
{ Eggs, Butter }
{Eggs, Cheese }
{Bread, Butter}
{Bread, Cheese}
{Butter, Cheese}
Support Count
2
5
3
2
3
2
1
4
3
1
T_id List of Item
1 { Milk, Eggs, Bread, Butter }
2 {Milk, Bread }
3 { Eggs, Bread, Butter }
4 {Milk, Bread, Butter }
5 { Milk, Bread, Cheese }
6 { Eggs, Bread, Cheese }
7 { Milk, Bread, Butter, Cheese}
8 { Milk, Eggs, }

30. Apriori Algorithm
Iteration 2:
• Join Step: Join 𝐿1 × 𝐿1 to generate
candidate itemset 𝐶2
• 𝒎𝒊𝒏_𝒔𝒖𝒑=3
• The set of frequent 2-itemsets, 𝐿2 ,
can then be determined.
• Prune Step: Remove all the itemsets
not satisfying minimum support.
• 𝐿2 consists Candidate 2-itemsets
satisfying minimum support.
𝑪𝟐
Item Support
Count
{ Milk, Eggs } 2
{ Milk, Bread } 5
{ Milk, Butter } 3
{ Milk, Cheese } 2
{ Eggs, Bread} 3
{ Eggs, Butter } 2
{Eggs, Cheese } 1
{Bread, Butter} 4
{Bread, Cheese} 3
{Butter, Cheese} 1
Item Support
Count
{ Milk, Eggs } 2
{ Milk, Bread } 5
{ Milk, Butter } 3
{ Milk, Cheese } 2
{ Eggs, Bread} 3
{ Eggs, Butter } 2
{Eggs, Cheese } 1
{Bread, Butter} 4
{Bread, Cheese} 3
{Butter, Cheese} 1
T_id List of Item
1 { Milk, Eggs, Bread, Butter }
2 {Milk, Bread }
3 { Eggs, Bread, Butter }
4 {Milk, Bread, Butter }
5 { Milk, Bread, Cheese }
6 { Eggs, Bread, Cheese }
7 { Milk, Bread, Butter, Cheese}
8 { Milk, Eggs, }

31. Apriori Algorithm
Iteration 2:
• Join Step: Join 𝐿1 × 𝐿1 to generate
candidate itemset 𝐶2
• 𝒎𝒊𝒏_𝒔𝒖𝒑=3
• The set of frequent 2-itemsets, 𝐿2 ,
can then be determined.
• Prune Step: Remove all the itemsets
not satisfying minimum support.
• 𝐿2 consists Candidate 2-itemsets
satisfying minimum support.
Item Support
Count
{ Milk, Bread } 5
{ Milk, Butter } 3
{ Eggs, Bread} 3
{Bread, Butter} 4
{Bread, Cheese} 3
Frequent 2-Itemset 𝑳𝟐
T_id List of Item
1 { Milk, Eggs, Bread, Butter }
2 {Milk, Bread }
3 { Eggs, Bread, Butter }
4 {Milk, Bread, Butter }
5 { Milk, Bread, Cheese }
6 { Eggs, Bread, Cheese }
7 { Milk, Bread, Butter, Cheese}
8 { Milk, Eggs, }

32. Apriori Algorithm
Iteration 3:
• Join Step: Join 𝐿2 × 𝐿2 to
generate candidate itemset
𝐶3.
𝑪𝟑
Item
{ Milk, Bread, Butter }
{ Milk, Eggs, Bread }
{ Milk, Bread, Cheese }
{ Eggs, Bread, Butter }
T_id List of Item
1 { Milk, Eggs, Bread, Butter }
2 {Milk, Bread }
3 { Eggs, Bread, Butter }
4 {Milk, Bread, Butter }
5 { Milk, Bread, Cheese }
6 { Eggs, Bread, Cheese }
7 { Milk, Bread, Butter, Cheese}
8 { Milk, Eggs, }

33. Apriori Algorithm
Iteration 3:
• Join Step: Join 𝐿2 × 𝐿2 to
generate candidate itemset 𝑪𝟑
• 𝒎𝒊𝒏_𝒔𝒖𝒑=3
• The set of frequent 3-itemsets,
𝐿3 , can then be determined.
• Prune Step: Remove all the
itemsets not satisfying
minimum support.
• 𝐿3 consists Candidate 3-
itemsets satisfying minimum
support.
𝑪𝟑
Item
{ Milk, Bread, Butter }
{ Milk, Eggs, Bread }
{ Milk, Bread, Cheese }
{ Eggs, Bread, Butter }
Item Support
Count
{ Milk, Bread, Butter } 3
{ Milk, Eggs, Bread } 1
{ Milk, Bread, Cheese } 2
{ Eggs, Bread, Butter } 2
Item Support
Count
{ Milk, Bread, Butter } 3
{ Milk, Eggs, Bread } 1
{ Milk, Bread, Cheese } 2
{ Eggs, Bread, Butter } 2
frequent 3-itemsets, 𝐿3
T_id List of Item
1 { Milk, Eggs, Bread, Butter }
2 {Milk, Bread }
3 { Eggs, Bread, Butter }
4 {Milk, Bread, Butter }
5 { Milk, Bread, Cheese }
6 { Eggs, Bread, Cheese }
7 { Milk, Bread, Butter, Cheese}
8 { Milk, Eggs, }

34. Apriori Algorithm
Iteration 3:
• Join Step: Join 𝐿2 × 𝐿2 to
generate candidate itemset 𝑪𝟑
• 𝒎𝒊𝒏_𝒔𝒖𝒑=3
• The set of frequent 3-itemsets,
𝐿3 , can then be determined.
• Prune Step: Remove all the
itemsets not satisfying
minimum support.
• 𝐿3 consists Candidate 3-
itemsets satisfying minimum
support.
Item Support
Count
{ Milk, Bread, Butter } 3
frequent 3-itemsets, 𝐿3
T_id List of Item
1 { Milk, Eggs, Bread, Butter }
2 {Milk, Bread }
3 { Eggs, Bread, Butter }
4 {Milk, Bread, Butter }
5 { Milk, Bread, Cheese }
6 { Eggs, Bread, Cheese }
7 { Milk, Bread, Butter, Cheese}
8 { Milk, Eggs, }

35. Algorithm:

36. Algorithm:

37. Generating Association Rules from Frequent
Itemsets
• To generate strong association rules from frequent itemsets, calculate confidence of
a rule using
𝑐𝑜𝑛𝑓𝑖𝑑𝑒𝑛𝑐𝑒 𝐴 ⟹ 𝐵 =
𝑆𝑢𝑝𝑝𝑜𝑟𝑡_𝑐𝑜𝑢𝑛𝑡(𝐴 ∪ 𝐵)
𝑆𝑢𝑝𝑝𝑜𝑟𝑡_𝑐𝑜𝑢𝑛𝑡(𝐴)
• Based on this, association rules can be generated as follows:
• For each frequent itemset 𝑙, generate all nonempty subsets of 𝑙.
• For every nonempty subset 𝑠 of 𝑙, output the rule 𝑠 ⟹ (𝑙 − 𝑠) if
𝑠𝑢𝑝𝑝𝑜𝑟𝑡−𝑐𝑜𝑢𝑛𝑡(𝑙)
𝑠𝑢𝑝𝑝𝑜𝑟𝑡_𝑐𝑜𝑢𝑛𝑡(𝑠)
≥ 𝑚𝑖𝑛 _𝑐𝑜𝑛𝑓,
where 𝑚𝑖𝑛 _𝑐𝑜𝑛𝑓 is the minimum confidence threshold

38. Generating Association Rules from Frequent
Itemsets
• E.g. Example contains frequent itemset 𝑙 = {𝑀𝑖𝑙𝑘, 𝐵𝑟𝑒𝑎𝑑, 𝐵𝑢𝑡𝑡𝑒𝑟}. What are the
association rules can be generated from 𝑙.
• Subsets of l = {milk}, {Bread}, {butter}, {Milk,Bread}, {Milk,Butter}, {Bread, Butter}
• Resulting association rules are
𝑀𝑖𝑙𝑘, 𝐵𝑟𝑒𝑎𝑑 ⟹ {𝐵𝑢𝑡𝑡𝑒𝑟}
𝑀𝑖𝑙𝑘, 𝐵𝑢𝑡𝑡𝑒𝑟 ⟹ {𝐵𝑟𝑒𝑎𝑑}
𝐵𝑟𝑒𝑎𝑑, 𝐵𝑢𝑡𝑡𝑒𝑟 ⟹ {𝑀𝑖𝑙𝑘}
𝑀𝑖𝑙𝑘 ⟹ {𝐵𝑟𝑒𝑎𝑑, 𝐵𝑢𝑡𝑡𝑒𝑟}
𝐵𝑟𝑒𝑎𝑑 ⟹ {𝑀𝑖𝑙𝑘, 𝐵𝑢𝑡𝑡𝑒𝑟}
𝐵𝑢𝑡𝑡𝑒𝑟 ⟹ {𝑀𝑖𝑙𝑘, 𝐵𝑟𝑒𝑎𝑑}
𝒄𝒐𝒏𝒇𝒊𝒅𝒆𝒏𝒄𝒆 = Τ
𝟑 𝟓 = 𝟔𝟎%
𝒄𝒐𝒏𝒇𝒊𝒅𝒆𝒏𝒄𝒆 = Τ
𝟑 𝟑 = 𝟏𝟎𝟎%
𝒄𝒐𝒏𝒇𝒊𝒅𝒆𝒏𝒄𝒆 = Τ
𝟑 𝟒 = 𝟕𝟓%
𝒄𝒐𝒏𝒇𝒊𝒅𝒆𝒏𝒄𝒆 = Τ
𝟑 𝟔 = 𝟓𝟎%
𝒄𝒐𝒏𝒇𝒊𝒅𝒆𝒏𝒄𝒆 = Τ
𝟑 𝟕 = 𝟒𝟐. 𝟖𝟓%
𝒄𝒐𝒏𝒇𝒊𝒅𝒆𝒏𝒄𝒆 = Τ
𝟑 𝟒 = 𝟕𝟓%
List of Item
{ Milk, Eggs, Bread, Butter }
{Milk, Bread }
{ Eggs, Bread, Butter }
{Milk, Bread, Butter }
{ Milk, Bread, Cheese }
{ Eggs, Bread, Cheese }
{ Milk, Bread, Butter, Cheese}
{ Milk, Eggs, }

39. Generating Association Rules from Frequent
Itemsets
Sr. No. Rule Confidence Is Strong Rule?
1 𝑀𝑖𝑙𝑘, 𝐵𝑟𝑒𝑎𝑑 ⟹ {𝐵𝑢𝑡𝑡𝑒𝑟} 60.00
2 𝑀𝑖𝑙𝑘, 𝐵𝑢𝑡𝑡𝑒𝑟 ⟹ {𝐵𝑟𝑒𝑎𝑑} 100.00
3 𝐵𝑟𝑒𝑎𝑑, 𝐵𝑢𝑡𝑡𝑒𝑟 ⟹ {𝑀𝑖𝑙𝑘} 75.00
4 𝑀𝑖𝑙𝑘 ⟹ {𝐵𝑟𝑒𝑎𝑑, 𝐵𝑢𝑡𝑡𝑒𝑟} 50.00
5 𝐵𝑟𝑒𝑎𝑑 ⟹ {𝑀𝑖𝑙𝑘, 𝐵𝑢𝑡𝑡𝑒𝑟} 42.85
6 𝐵𝑢𝑡𝑡𝑒𝑟 ⟹ {𝑀𝑖𝑙𝑘, 𝐵𝑟𝑒𝑎𝑑} 75.00
Minimum Confidence is
60%
Rule Confidence
𝑀𝑖𝑙𝑘, 𝐵𝑟𝑒𝑎𝑑 ⟹ {𝐵𝑢𝑡𝑡𝑒𝑟} 60.00
𝑀𝑖𝑙𝑘, 𝐵𝑢𝑡𝑡𝑒𝑟 ⟹ {𝐵𝑟𝑒𝑎𝑑} 100.00
𝐵𝑟𝑒𝑎𝑑, 𝐵𝑢𝑡𝑡𝑒𝑟 ⟹ {𝑀𝑖𝑙𝑘} 75.00
𝑀𝑖𝑙𝑘 ⟹ {𝐵𝑟𝑒𝑎𝑑, 𝐵𝑢𝑡𝑡𝑒𝑟} 50.00
𝐵𝑟𝑒𝑎𝑑 ⟹ {𝑀𝑖𝑙𝑘, 𝐵𝑢𝑡𝑡𝑒𝑟} 42.85
𝐵𝑢𝑡𝑡𝑒𝑟 ⟹ {𝑀𝑖𝑙𝑘, 𝐵𝑟𝑒𝑎𝑑} 75.00

40. Minimum Support = 30% and Minimum Confidence = 65%

41. Methods to Improve Efficiency of Apriori
Hash Based Technique
Transaction reduction
Partitioning
Dynamic Itemset Counting
Sampling

42. • Hash Based Technique
• Can be used to reduce the size of the candidate 𝑘-itemsets, 𝐶𝑘, for 𝑘 > 1.
• Such a hash-based technique may substantially reduce the number of the candidate
𝑘 −itemsets examined (especially when 𝑘 = 2).
• In 2nd iteration, i.e. generation of 2-itemset, every combination of two items, map them on
different buckets of a hash table structure and increment the bucket count.
• If count of bucket is less than min_sup count, then remove them from candidate sets.
Methods to Improve Efficiency of Apriori

43. • Hash Based Technique
TID List of Items
T1 A, B, E
T2 B, D
T3 B, C
T4 A, B, D
T5 A, C
T6 B, C
T7 A, C
T8 A, B, C, E
T9 A, B, C
𝐦𝐢𝐧 _𝐬𝐮𝐩 𝐂𝐨𝐮𝐧𝐭 = 𝟑
Itemset Support Count
A 6
B 7
C 6
D 2
E 2
𝑪𝟏
Order of items
A = 1, B = 2, C = 3, D = 4 and E = 5
Itemset Count Hash Function
A,B 4 1 × 10 + 2 𝑚𝑜𝑑 7 = 𝟓
A,C 4 1 × 10 + 3 𝑚𝑜𝑑 7 = 𝟔
A,D 1 1 × 10 + 4 𝑚𝑜𝑑 7 = 𝟎
A,E 2 1 × 10 + 5 𝑚𝑜𝑑 7 = 𝟏
B,C 4 2 × 10 + 3 𝑚𝑜𝑑 7 = 𝟐
B,D 2 2 × 10 + 4 𝑚𝑜𝑑 7 = 𝟑
B,E 2 2 × 10 + 5 𝑚𝑜𝑑 7 = 𝟒
C,D 0 −
C,E 1 3 × 10 + 5 𝑚𝑜𝑑 7 = 𝟎
D,E 0 −
𝑯 𝒙, 𝒚 = (𝒐𝒓𝒅𝒆𝒓 𝒐𝒇 𝒙 × 𝟏𝟎 + (𝒐𝒓𝒅𝒆𝒓 𝒐𝒇 𝒚)) 𝒎𝒐𝒅 𝟕
Hash Table
Methods to Improve Efficiency of Apriori

44. • Hash Based Technique
Bucket
Address
Bucket
Count
Bucket
Content
𝑳𝟐
0 2 {A,D} {C,E} No
1 2 {A,E} {A,E} No
2 4
{B,C} {B,C} {B,C}
{B,C}
Yes
3 2 {B, D} {B,D} No
4 2 {B,E} {B,E} No
5 4
{A,B} {A,B} {A,B}
{A,B}
Yes
6 4
{A,C} {A,C} {A,C}
{A,C}
yes
Hash Table Structure to Generate 𝑳𝟐
𝐦𝐢𝐧 _𝐬𝐮𝐩 𝐂𝐨𝐮𝐧𝐭 = 𝟑
TID List of Items
T1 {A, B, E}
T2 {B, D}
T3 {B, C}
T4 {A, B, D}
T5 {A, C}
T6 {B, C}
T7 {A, C}
T8 {A, B, C, E}
T9 {A, B, C}
Methods to Improve Efficiency of Apriori
Itemset Hash
Value
{A,B} 𝟓
{A,C} 𝟔
{A,D} 𝟎
{A,E} 𝟏
{B,C} 𝟐
{B,D} 𝟑
{B,E} 𝟒
{C,E} 𝟎

45. • Transaction Reduction
• A transaction that does not contain any frequent 𝑘-itemsets cannot contain any frequent
(𝑘 + 1)-itemsets.
• Such transaction can be marked or removed from further consideration
TID List of
Items
T1 A, B, E
T2 B, C, D
T3 C, D
T4 A, B, C, D
TID A B C D E
T1 1 1 0 0 1 3
T2 0 1 1 1 0 3
T3 0 0 1 1 0 2
T4 1 1 1 1 0 4
2 3 3 3 1
𝐦𝐢𝐧 _𝐬𝐮𝐩 𝐂𝐨𝐮𝐧𝐭 = 𝟐
TID A B C D E
T1 1 1 0 0 1
T2 0 1 1 1 0
T3 0 0 1 1 0
T4 1 1 1 1 0
TID A B C D
T1 1 1 0 0
T2 0 1 1 1
T3 0 0 1 1
T4 1 1 1 1
Methods to Improve Efficiency of Apriori

46. • Transaction Reduction
TID List of Items
T1 A, B, E
T2 B, C, D
T3 C, D
T4 A, B, C, D
TID A,B A,C A,D B,C B,D C,D
T1 1 0 0 0 0 0 1
T2 0 0 0 1 1 1 3
T3 0 0 0 0 0 1 1
T4 1 1 1 1 1 1 6
2 1 1 2 2 3
𝐦𝐢𝐧 _𝐬𝐮𝐩 𝐂𝐨𝐮𝐧𝐭 = 𝟐
TID A,B A,C A,D B,C B,D C,D
T1 1 0 0 0 0 0 1
T2 0 0 0 1 1 1 3
T3 0 0 0 0 0 1 1
T4 1 1 1 1 1 1 6
2 1 1 2 2 3
TID A,B B,C B,D C,D
T2 0 1 1 1
T4 1 1 1 1
TID A,B B,C B,D C,D
T2 0 1 1 1 3
T4 1 1 1 1 4
1 2 2 2
TID B,C,D
T2 1
T4 1
TID B,C B,D C,D
T2 1 1 1
T4 1 1 1
Methods to Improve Efficiency of Apriori

47. • Partitioning
• Requires just two database scans to mine frequent itemsets
Transactions
in D
Frequent
itemsets in
D
Find global
frequent
itemsets
among
candidates
(1 Scan)
Combine all
frequent
itemsets to
form
candidate
itemset
Find frequent
Itemsets local
to each
partitions
(1 Scan)
Divide D into
n partitions
Transactions
in D
Phase I
Phase II
Methods to Improve Efficiency of Apriori

48. • Partitioning
Transactions
in D
TID A B C D E
T1 1 0 0 0 1
T2 0 1 0 1 0
T3 0 0 0 1 1
T4 0 1 1 0 0
T5 0 0 0 0 1
T6 0 1 1 1 0
Database is divided into three partitions
Each having two transactions with
support of 20%
First Scan
Support = 20%
Min_Sup = 1
A=1, B=1, D=1, E=1
{A,E} = 1, {B,D} = 1
B=1, C=1, D=1, E=1
{D,E} = 1, {B,C} = 1
B=1, C=1, D=1, E=1
{B,C}=1, {B,D}=1, {C,D} = 1
{B,C,D} = 1
Shortlisted
Frequent
Itemsets
B=3,
C=2,
D=3,
E=3
{B,D} = 2
{B,C} = 2
Second Scan
Support = 20%
Min_Sup = 2
A=1, B=3, C=2, D=3, E=3
{A,E} = 1
{B,D} = 2
{D,E} = 1
{B,C} = 2
{C,D} = 1
{B,C,D} = 1
Methods to Improve Efficiency of Apriori

49. • Dynamic Itemset Counting
• Database is partitioned into blocks marked by start points.
• New candidate can be added at any start point.
• This technique uses the count-so-far as the lower bound of the actual count
• If the count-so-far passes the min_sup, the itemset is added into frequent itemset collection
and can be used to generate longer candidates
• Leads to fewer database scans
Transactions
in D
Methods to Improve Efficiency of Apriori

50. C
B
• Dynamic Itemset Counting
Transactions
in D
TID List of Items
T1 A, B,
T2 B, C
T3 A
T4 -
TID A B C
T1 1 1 0
T2 0 1 1
Minimum Support = 25%
Number of blocks (M) = 2
{ }
A
A,B A,C B,C
A,B,C
Confirmed Frequent Itemset
Suspected Frequent Itemset
Confirmed Infrequent Itemset
Suspected Infrequent Itemset
{ }
A B C
A,B A,C B,C
A,B,C
A,C
{ }
A B C
A,B B,C
A,B,C
A=0, B=0, C=0 A=1, B=2, C=1
AB=1, BC = 1
A=2, B=2, C=1
AB=1, BC = 1
Itemset Lattice
Before scanning
Itemset Lattice after
scanning 1st block
Itemset Lattice after
scanning 1st and 2nd block
Methods to Improve Efficiency of Apriori
TID List of Items
T1 A, B,
T2 B, C
T3 A
T4 -
T3 1 0 0
T4 0 0 0

51. • Sampling
• Pick up a random sample S of a given dataset D,
• Search for frequent itemsets in S instead of D
• We trade off some degree of accuracy against efficiency.
• We may lose a global frequent itemset, so we use a lower support threshold than minimum
support to find frequent itemsets local to S denoted as 𝐿𝑆
.
• The rest of the database is used to compute the actual frequencies of each itemset in 𝐿𝑆.
• If 𝐿𝑆
contains all frequent itemsets in D, then only one scan of D is required.
Transactions
in D
Methods to Improve Efficiency of Apriori

52. • Reducing the size of candidate sets may lead to good performance, it can suffer
from two nontrivial costs:
• It may still need to generate a huge number of candidate sets.
• It may need to repeatedly scan the whole databases and check a large set of candidate by
pattern matching.
• A method is required that will mine the complete set of frequent itemsets
without a costly candidate generation process
• This method is called as Frequent Pattern Growth or FP-Growth
FP-Growth

53. • Adopts a divide-and-conquer strategy as:
• First it compresses the database representing frequent items into a frequent pattern tree or
FP-tree which retains itemset association information
• Then it divides the compressed database into a set of conditional databases, each associated
with one frequent item or pattern fragment
• And then mines each database separately.
FP-Growth

54. FP-Growth
TID List of Items
T1 A, B, E
T2 B, D
T3 B, C
T4 A, B, D
T5 A, C
T6 B, C
T7 A, C
T8 A, B, C, E
T9 A, B, C
Itemset Support
B 7
A 6
C 6
D 2
E 2
Scan the database
Derive set of frequent 1-
itemset and their support
count (min_sup=2)
Itemset Support
A 6
B 7
C 6
D 2
E 2
Sort in order of
descending support
count
𝐿 = { 𝐵: 7 , 𝐴: 6 , 𝐶: 6 , 𝐷: 2 , {𝐸: 2}}

55. FP-Growth
TID List of Items
T1 A, B, E
T2 B, D
T3 B, C
T4 A, B, D
T5 A, C
T6 B, C
T7 A, C
T8 A, B, C, E
T9 A, B, C
Itemset Support
B 7
A 6
C 6
D 2
E 2
1. Create the root of the
tree, labeled with “null”
2. Scan the database D again.
The items in each transaction
are processed in L order
null { }
𝐿 = { 𝐵: 7 , 𝐴: 6 , 𝐶: 6 , 𝐷: 2 , {𝐸: 2}}

56. FP-Growth
TID List of Items
T1 A, B, E
T2 B, D
T3 B, C
T4 A, B, D
T5 A, C
T6 B, C
T7 A, C
T8 A, B, C, E
T9 A, B, C
Itemset Support
B 7
A 6
C 6
D 2
E 2
1. Create the root of the
tree, labeled with “null”
2. Scan the database D again.
The items in each transaction
are processed in L order
null { }
B: 1
A: 1
E: 1
𝐿 = { 𝐵: 7 , 𝐴: 6 , 𝐶: 6 , 𝐷: 2 , {𝐸: 2}}

57. FP-Growth
TID List of Items
T1 A, B, E
T2 B, D
T3 B, C
T4 A, B, D
T5 A, C
T6 B, C
T7 A, C
T8 A, B, C, E
T9 A, B, C
Itemset Support
B 7
A 6
C 6
D 2
E 2
1. Create the root of the
tree, labeled with “null”
2. Scan the database D again.
The items in each transaction
are processed in L order
null { }
B: 2
A: 1
E: 1
D: 1
B: 2
D: 1
𝐿 = { 𝐵: 7 , 𝐴: 6 , 𝐶: 6 , 𝐷: 2 , {𝐸: 2}}

58. FP-Growth
TID List of Items
T1 A, B, E
T2 B, D
T3 B, C
T4 A, B, D
T5 A, C
T6 B, C
T7 A, C
T8 A, B, C, E
T9 A, B, C
Itemset Support
B 7
A 6
C 6
D 2
E 2
1. Create the root of the
tree, labeled with “null”
2. Scan the database D again.
The items in each transaction
are processed in L order
null { }
B: 3
A: 1
E: 1
D: 1
C: 1

59. FP-Growth
TID List of Items
T1 A, B, E
T2 B, D
T3 B, C
T4 A, B, D
T5 A, C
T6 B, C
T7 A, C
T8 A, B, C, E
T9 A, B, C
Itemset Support
B 7
A 6
C 6
D 2
E 2
1. Create the root of the
tree, labeled with “null”
2. Scan the database D again.
The items in each transaction
are processed in L order
null { }
B: 4
A: 2
E: 1
D: 1
C: 1
D: 1

60. FP-Growth
TID List of Items
T1 A, B, E
T2 B, D
T3 B, C
T4 A, B, D
T5 A, C
T6 B, C
T7 A, C
T8 A, B, C, E
T9 A, B, C
Itemset Support
B 7
A 6
C 6
D 2
E 2
1. Create the root of the
tree, labeled with “null”
2. Scan the database D again.
The items in each transaction
are processed in L order
null { }
B: 4
A: 2
E: 1
D: 1
C: 1
D: 1
A: 1
C: 1

61. FP-Growth
TID List of Items
T1 A, B, E
T2 B, D
T3 B, C
T4 A, B, D
T5 A, C
T6 B, C
T7 A, C
T8 A, B, C, E
T9 A, B, C
Itemset Support
B 7
A 6
C 6
D 2
E 2
1. Create the root of the
tree, labeled with “null”
2. Scan the database D again.
The items in each transaction
are processed in L order
null { }
B: 5
A: 2
E: 1
D: 1
C: 2
D: 1
A: 1
C: 1

62. FP-Growth
TID List of Items
T1 A, B, E
T2 B, D
T3 B, C
T4 A, B, D
T5 A, C
T6 B, C
T7 A, C
T8 A, B, C, E
T9 A, B, C
Itemset Support
B 7
A 6
C 6
D 2
E 2
1. Create the root of the
tree, labeled with “null”
2. Scan the database D again.
The items in each transaction
are processed in L order
null { }
B: 5
A: 2
E: 1
D: 1
C: 2
D: 1
A: 2
C: 2

63. FP-Growth
TID List of Items
T1 A, B, E
T2 B, D
T3 B, C
T4 A, B, D
T5 A, C
T6 B, C
T7 A, C
T8 A, B, C, E
T9 A, B, C
Itemset Support
B 7
A 6
C 6
D 2
E 2
1. Create the root of the
tree, labeled with “null”
2. Scan the database D again.
The items in each transaction
are processed in L order
null { }
B: 6
A: 3
E: 1
D: 1
C: 2
D: 1
C: 1
E: 1
A: 2
C: 2

64. FP-Growth
TID List of Items
T1 A, B, E
T2 B, D
T3 B, C
T4 A, B, D
T5 A, C
T6 B, C
T7 A, C
T8 A, B, C, E
T9 A, B, C
Itemset Support
B 7
A 6
C 6
D 2
E 2
1. Create the root of the
tree, labeled with “null”
2. Scan the database D again.
The items in each transaction
are processed in L order
null { }
B: 7
A: 4
E: 1
D: 1
C: 2
D: 1
C: 2
E: 1
A:2
C: 2

65. FP-Growth
TID List of Items
T1 A, B, E
T2 B, D
T3 B, C
T4 A, B, D
T5 A, C
T6 B, C
T7 A, C
T8 A, B, C, E
T9 A, B, C
Itemset Support
B 7
A 6
C 6
D 2
E 2
1. Create the root of the
tree, labeled with “null”
2. Scan the database D again.
The items in each transaction
are processed in L order
null { }
B: 7
A: 4
E: 1
D: 1
C: 2
D: 1
C: 2
E: 1
A:2
C: 2

66. FP-Growth
Itemset Support Node
Link
B 7
A 6
C 6
D 2
E 2
To facilitate tree traversal, an item header table is built so that each item points to occurrences in the tree via a
chain of node-links.
null { }
B: 7
A: 4
E: 1
D: 1
C: 2
D: 1
C: 2
E: 1
A:2
C: 2

67. Home Work
• Draw FP-tree for given database TID List of Items
T1 {A,B}
T2 {B,C}
T3 {B,C,D}
T4 {A,C,D,E}
T5 {A,D,E}
T6 {A,B,C}
T7 {A,B,C,D}
T8 {A,C}
T9 {A,B,C}
T10 {A,D,E}
T11 {A,E}

68. Home Work

69. FP-Growth
• The FP-tree is mined as follows
• Start from each frequent length-1 pattern (as an initial suffix pattern), construct its
conditional pattern base (a “subdatabase,”which consists of the set of prefix paths in the FP-
tree co-occurring with the suffix pattern),
• Then construct its (conditional) FP-tree,
• perform mining recursively on such a tree.
• The pattern growth is achieved by the concatenation of the suffix pattern with
the frequent patterns generated from a conditional FP-tree.

70. FP-Growth
Item Conditional Pattern Base Conditional FP-Tree Frequent Patterns Generated
E 𝐵, 𝐴: 1 , 𝐵, 𝐴, 𝐶: 1 𝐵: 2, 𝐴: 2 𝐵, 𝐸: 2 , 𝐴, 𝐸: 2 , {𝐵, 𝐴, 𝐸: 2}
D 𝐵: 1 , 𝐵, 𝐴: 1 𝐵: 2 𝐵, 𝐷: 2
C 𝐵, 𝐴: 2 , 𝐵: 2 , {𝐴: 2} 𝐵: 4, 𝐴: 2 , 𝐴: 2 𝐵, 𝐶: 4 , 𝐴, 𝐶: 4 , 𝐵, 𝐴, 𝐶: 2
A 𝐵: 4 𝐵: 4 𝐵, 𝐴: 4
B - - -
1. Start with Item having least support count
2. Generate conditional pattern base by
identifying the path to the item
3. Form conditional FP-Tree
4. Generate frequent patterns

71. Mining Frequent Itemsets Using Vertical
Data Format
TID List of Items
T1 A, B, E
T2 B, D
T3 B, C
T4 A, B, D
T5 A, C
T6 B, C
T7 A, C
T8 A, B, C, E
T9 A, B, C
Item TID_set
A {T1, T4, T5, T7, T8, T9}
B {T1, T2, T3, T4, T6, T8, T9}
C {T3, T5, T6, T7, T8, T9}
D {T2, T4}
E {T1, T8}
Horizontal Data Format
{𝑇𝐼𝐷: 𝐼𝑡𝑒𝑚𝑠𝑒𝑡}
Vertical Data Format
{𝐼𝑡𝑒𝑚: 𝑇𝐼𝐷_𝑠𝑒𝑡}
Mining can be performed on this data set
by intersecting the TID sets of every pair of
frequent single items.
Item TID_set
A∩B {T1, T4, T8, T9}
A∩C {T5, T7, T8, T9}
A∩D {T4}
A∩E {T1, T8}
B∩C {T3, T6, T8, T9}
B∩D {T2, T4}
B∩E {T1, T8}
C∩D { }
C∩E {T8}
D∩E {}

72. Mining Frequent Itemsets Using Vertical
Data Format
Item TID_set
{A, B} {T1, T4, T8, T9}
{A, C} {T5, T7, T8, T9}
{A, D} {T4}
{A, E} {T1, T8}
{B, C} {T3, T6, T8, T9}
{B, D} {T2, T4}
{B, E} {T1, T8}
{C, E} {T8}
2-Itemset in vertical format
Item TID_set
{A, B, C, E} {T8}
3-Itemset in vertical format
4-Itemset in vertical format
There are only two frequent 3-itemsets:
𝑨, 𝑩, 𝑪: 𝟐 and 𝑨, 𝑩, 𝑬: 𝟐
Item TID_set
{A, B} {T1, T4, T8, T9}
{A, C} {T5, T7, T8, T9}
{A, D} {T4}
{A, E} {T1, T8}
{B, C} {T3, T6, T8, T9}
{B, D} {T2, T4}
{B, E} {T1, T8}
{C, E} {T8}
Item TID_set
{A, B, C} {T8, T9}
{A, B, E} {T1, T8}
Item TID_set
{A, B, C, E} {T8}
The support count of an itemset is simply the length of
the TID_set of the itemset.

73. TID Itemset
1 D, B
2 C, A, B
3 D, A, B, C
4 A, C
5 D, C
6 C, A, E
7 D, C, A
8 D
9 A, B, D
10 B, C, E
11 B, A
Find the frequent itemsets using FP-Growth algorithm with minimum support= 50%

74. Mining Multilevel Association Rules
• Strong associations discovered at high levels of abstraction may represent
commonsense knowledge.
• So, data mining systems should provide capabilities for mining association rules at
multiple levels of abstraction, with sufficient flexibility for easy traversal among
different abstraction spaces.

75. Mining Multilevel Association Rules

76. Mining Multilevel Association Rules
Concept Hierarchy for Computer Items at Shop
Level 0
Level 1
Level 2
Level 3
Level 4

77. Mining Multilevel Association Rules
• It is difficult to find interesting purchase patterns at such raw or primitive-level
data.
• It is easier to find strong associations between generalized abstractions of these
items at primitive levels.
• Association rules generated from mining data at multiple levels of abstraction are
called multiple-level or multilevel association rules.
• Multilevel association rules can be mined efficiently using concept hierarchies
under a support-confidence framework.
• A top-down strategy is employed.

78. Mining Multilevel Association Rules
• Using uniform minimum support for all levels:
• The same minimum support threshold is used when mining at each level of abstraction.
• The search procedure is simplified.
• If min_sup is set too high, it could miss some meaningful associations at low abstraction levels
• If min_sup is set too low, it may generate many uninteresting associations at high abstraction
levels

79. Mining Multilevel Association Rules
• Using reduced minimum support at lower levels:
• Each level of abstraction has its own minimum support threshold.
• The deeper the level of abstraction, the smaller the corresponding threshold is

80. Mining Multilevel Association Rules
• Using item or group-based minimum support:
• It is sometimes more desirable to set up user-specific, item, or group based minimal support
thresholds when mining multilevel rules
• e.g. a user could set up the minimum support thresholds based on product price, or on items of
interest, such as by setting particularly low support thresholds for laptop computers and flash
drives in order to pay particular attention to the association patterns containing items in these
categories.
• A serious side effect of mining multilevel association rules is its generation of many
redundant rules across multiple levels of abstraction due to the “ancestor”
relationships among items.

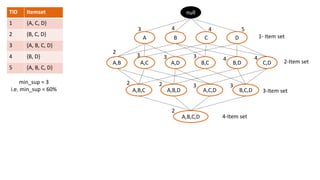
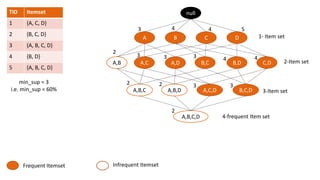
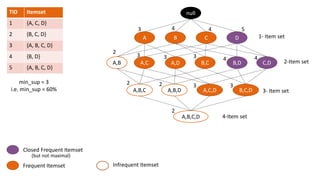
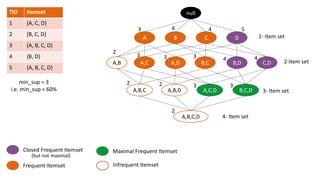
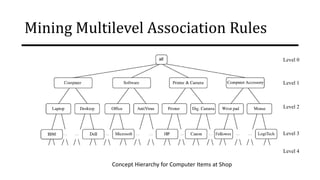
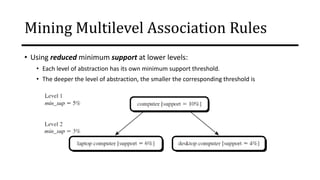
81. Mining Multilevel Association Rules
• A serious side effect of mining multilevel association rules is its generation of many
redundant rules across multiple levels of abstraction due to the “ancestor”
relationships among items.
𝑏𝑢𝑦𝑠(𝑋, "Laptop computer") ⇒ 𝑏𝑢𝑦𝑠(𝑋, "HP Printer")
[𝑠𝑢𝑝𝑝𝑜𝑟𝑡 = 8%, 𝑐𝑜𝑛𝑓𝑖𝑑𝑒𝑛𝑐𝑒 = 70%]
𝑏𝑢𝑦𝑠(𝑋, "IBM Laptop computer") ⇒ 𝑏𝑢𝑦𝑠(𝑋, "HP Printer")
[𝑠𝑢𝑝𝑝𝑜𝑟𝑡 = 2%, 𝑐𝑜𝑛𝑓𝑖𝑑𝑒𝑛𝑐𝑒 = 72%]
• Does the later rule really provide any novel information??
• A rule 𝑅1 is an ancestor of a rule 𝑅2, if 𝑅1 can be obtained by replacing the items in
𝑅2 by their ancestors in a concept hierarchy.

82. Mining Multidimensional Association Rules
• Single Dimensional Rule
𝑏𝑢𝑦𝑠(𝑋, "Milk") ⇒ buys(X,"𝐵𝑢𝑡𝑡𝑒𝑟")
• Instead of considering transaction data only, sales and related information are also
linked with relational data in data warehouse.
• Such data stores are multidimensional in nature
• Additional information of customers who purchased the items may also be stored.
• We can mine association rules containing multiple predicates/dimesions
𝒂𝒈𝒆(𝑋, "20−29" ) ∧ 𝒐𝒄𝒄𝒖𝒑𝒂𝒕𝒊𝒐𝒏(𝑋, "Housewife") ⇒ 𝒃𝒖𝒚𝒔(𝑋, "Milk" )
• Association rules which involve two or more dimensions or predicates are referred
as multidimensional association rules.

83. Mining Multidimensional Association Rules
𝒂𝒈𝒆(𝑋, "20−29" ) ∧ 𝒐𝒄𝒄𝒖𝒑𝒂𝒕𝒊𝒐𝒏(𝑋, "Housewife") ⇒ 𝒃𝒖𝒚𝒔(𝑋, "Milk" )
• No repeated predicates.
• Association rules which involve with no repeated predicates are referred as
interdimensional association rules.
• Association rules with repeated predicates are called as Hybrid-dimensional
association rules
𝒂𝒈𝒆(𝑋, "20−29" ) ∧ 𝒃𝒖𝒚𝒔(𝑋, "Milk") ⇒ 𝒃𝒖𝒚𝒔(𝑋, "Bread" )

84. Mining Multidimensional Association Rules
• Data attributes can be nominal or quantitative.
• Mining multidimensional association rules (with quantitative attributes) can be
categorized in to two approaches
1. Mining multidimensional association rules using Static discretization of
quantitative attributes
• Quantitative attributes are discretization using predefined concept hierarchies
• Discretization is done before mining.
2. Mining multidimensional association rules using Dynamic discretization of
quantitative attributes
• Quantitative attributes are discretization or clustered into bins based on the data distribution
• Bins may be combined during the mining process, that’s why dynamic process.