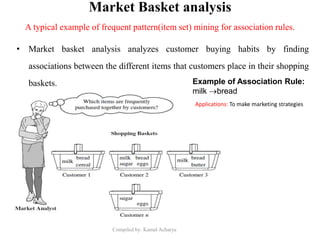
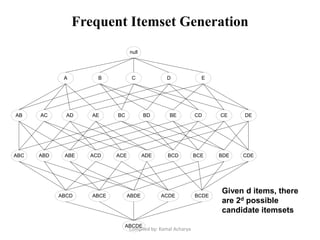
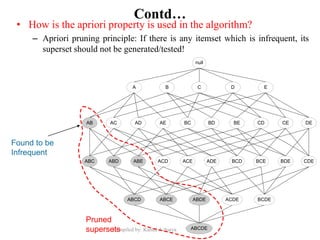
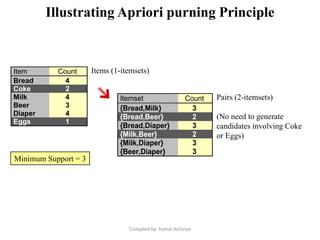
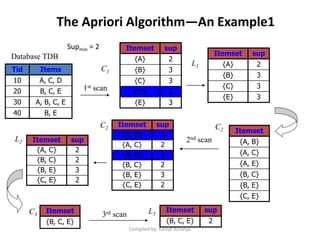
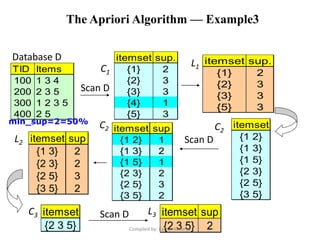
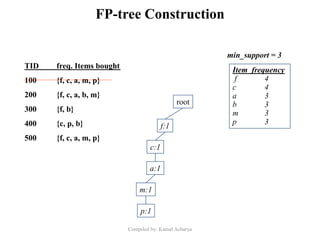
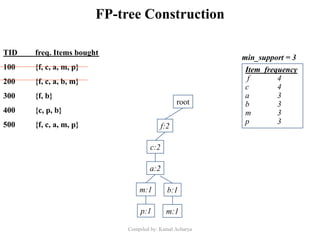
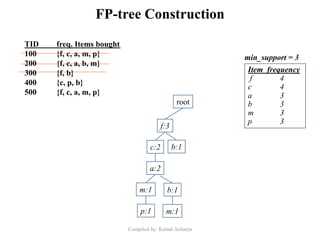
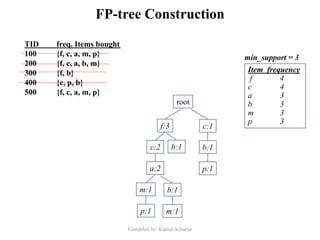
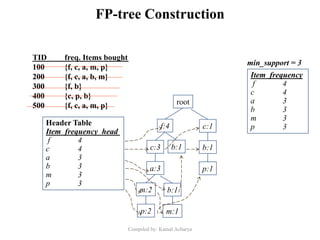
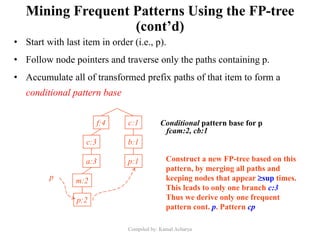
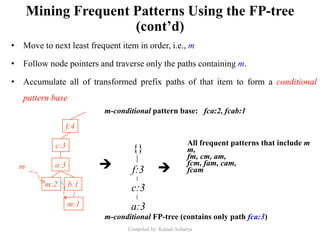
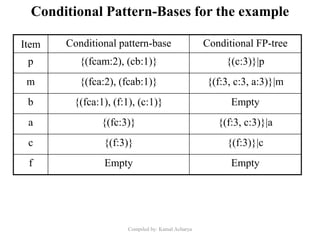
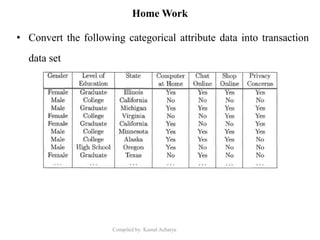
Association analysis is a technique used to uncover relationships between items in transactional data. It involves finding frequent itemsets whose occurrence exceeds a minimum support threshold, and then generating association rules from these itemsets that satisfy minimum confidence. The Apriori algorithm is commonly used for this task, as it leverages the Apriori property to prune the search space - if an itemset is infrequent, its supersets cannot be frequent. It performs multiple database scans to iteratively grow frequent itemsets and extract high confidence rules.