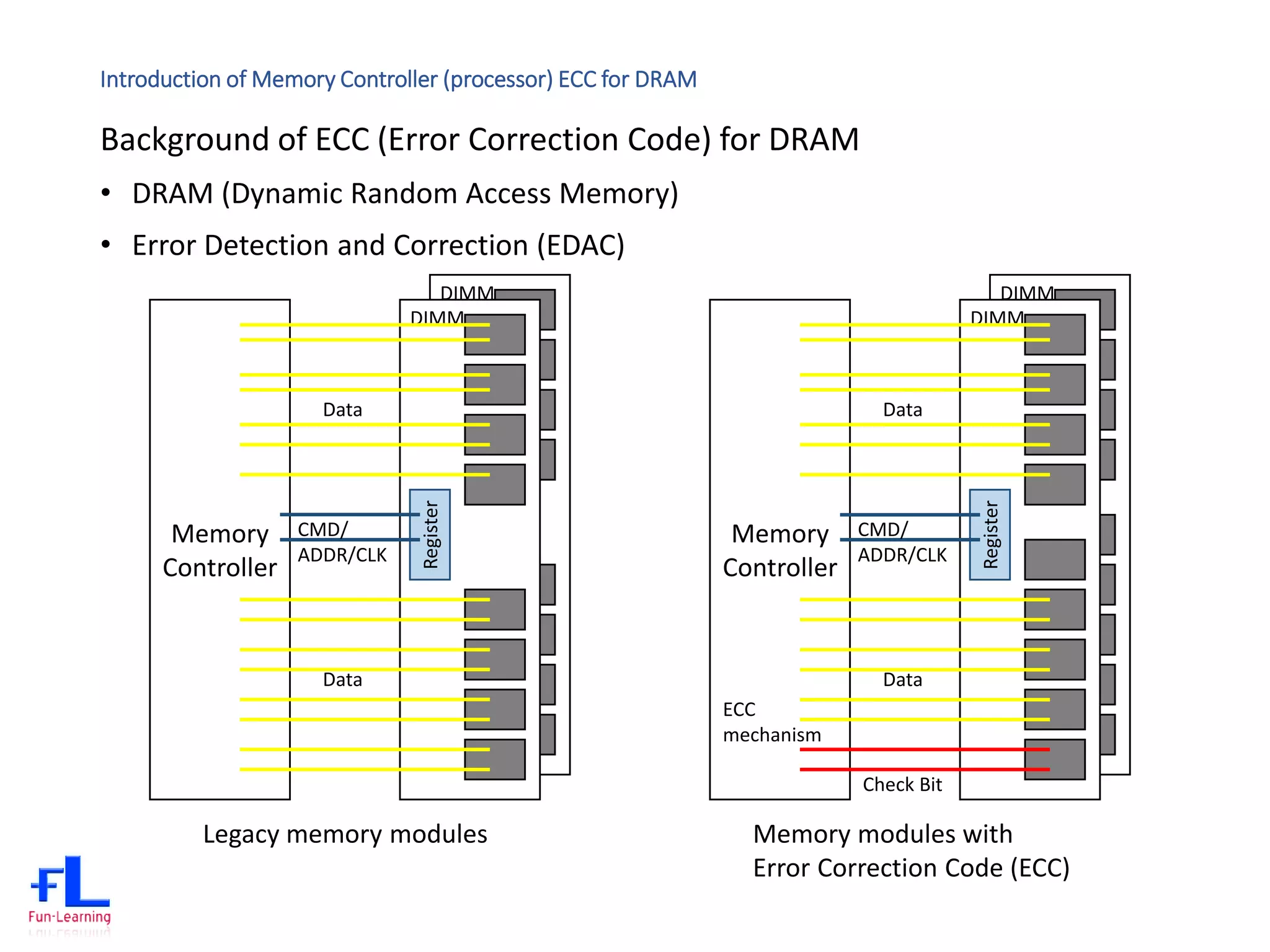
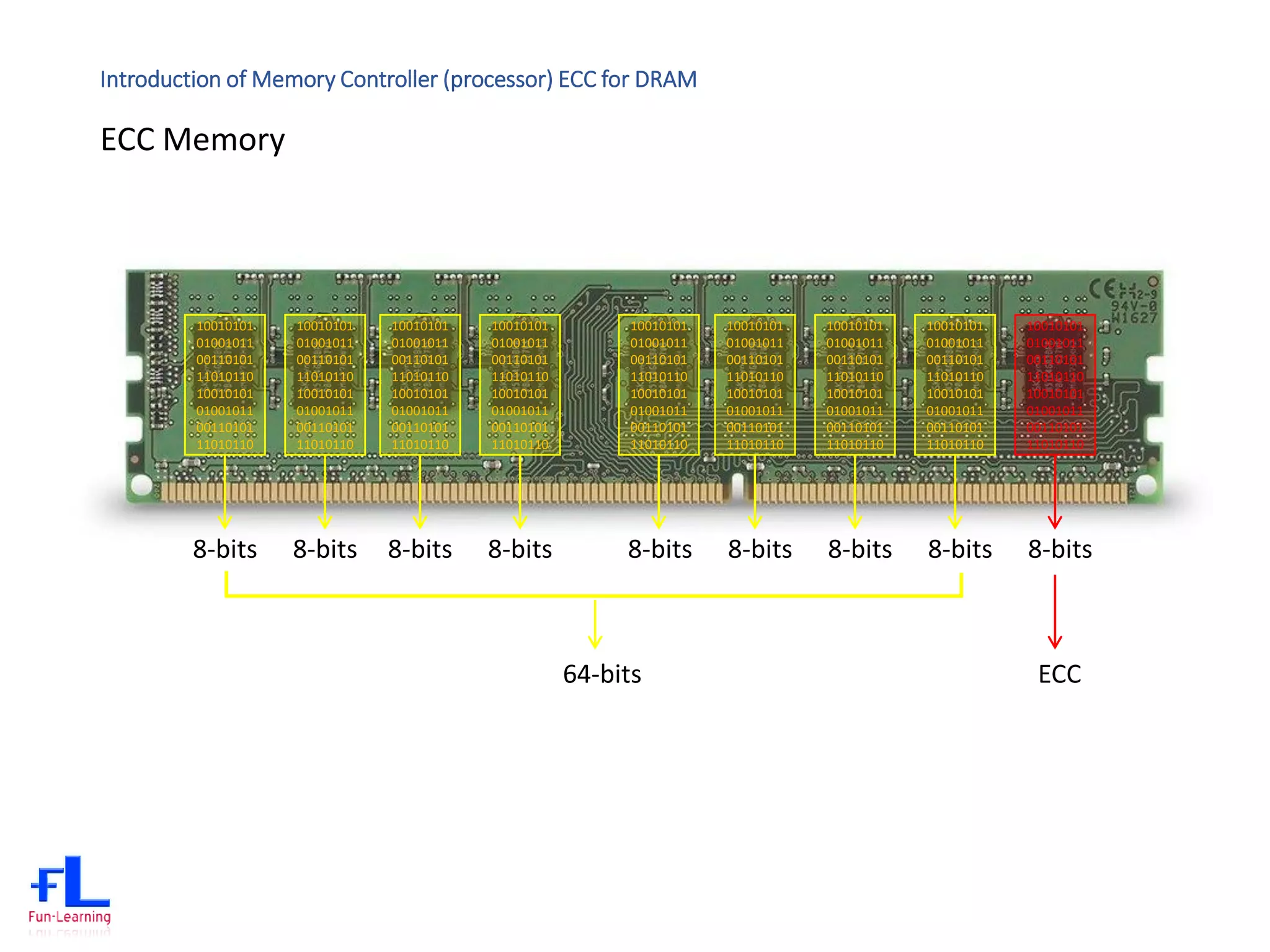
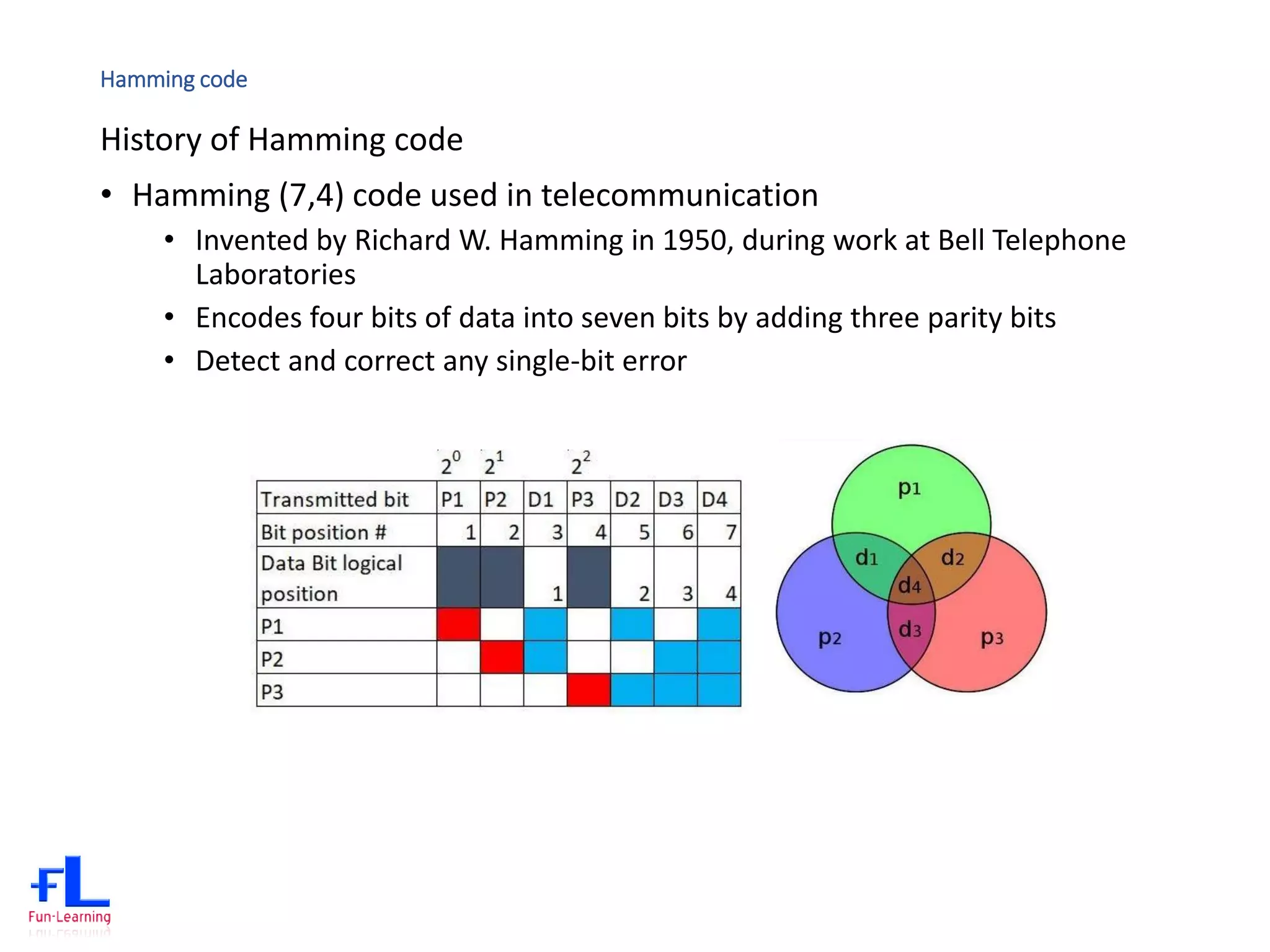
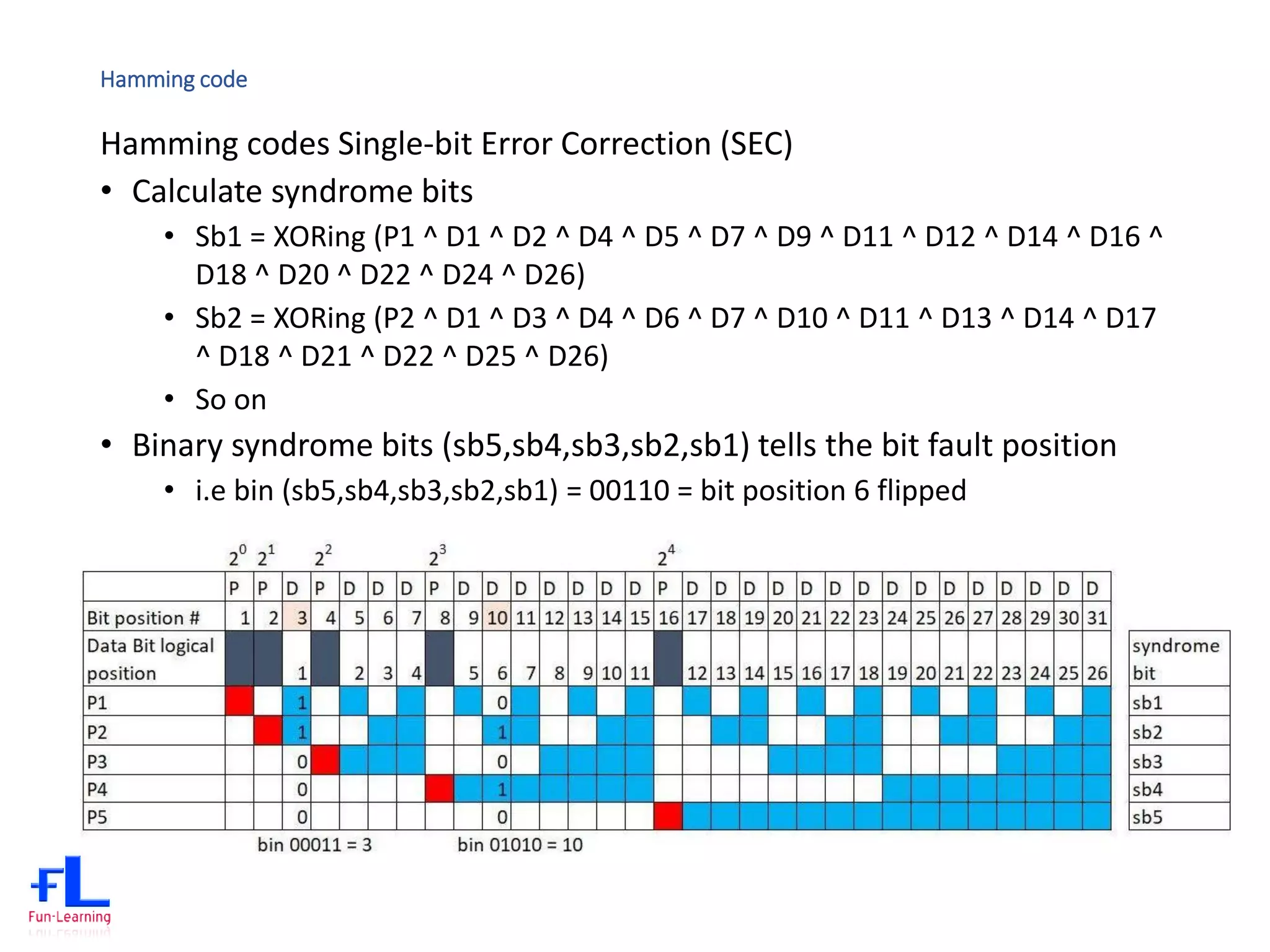
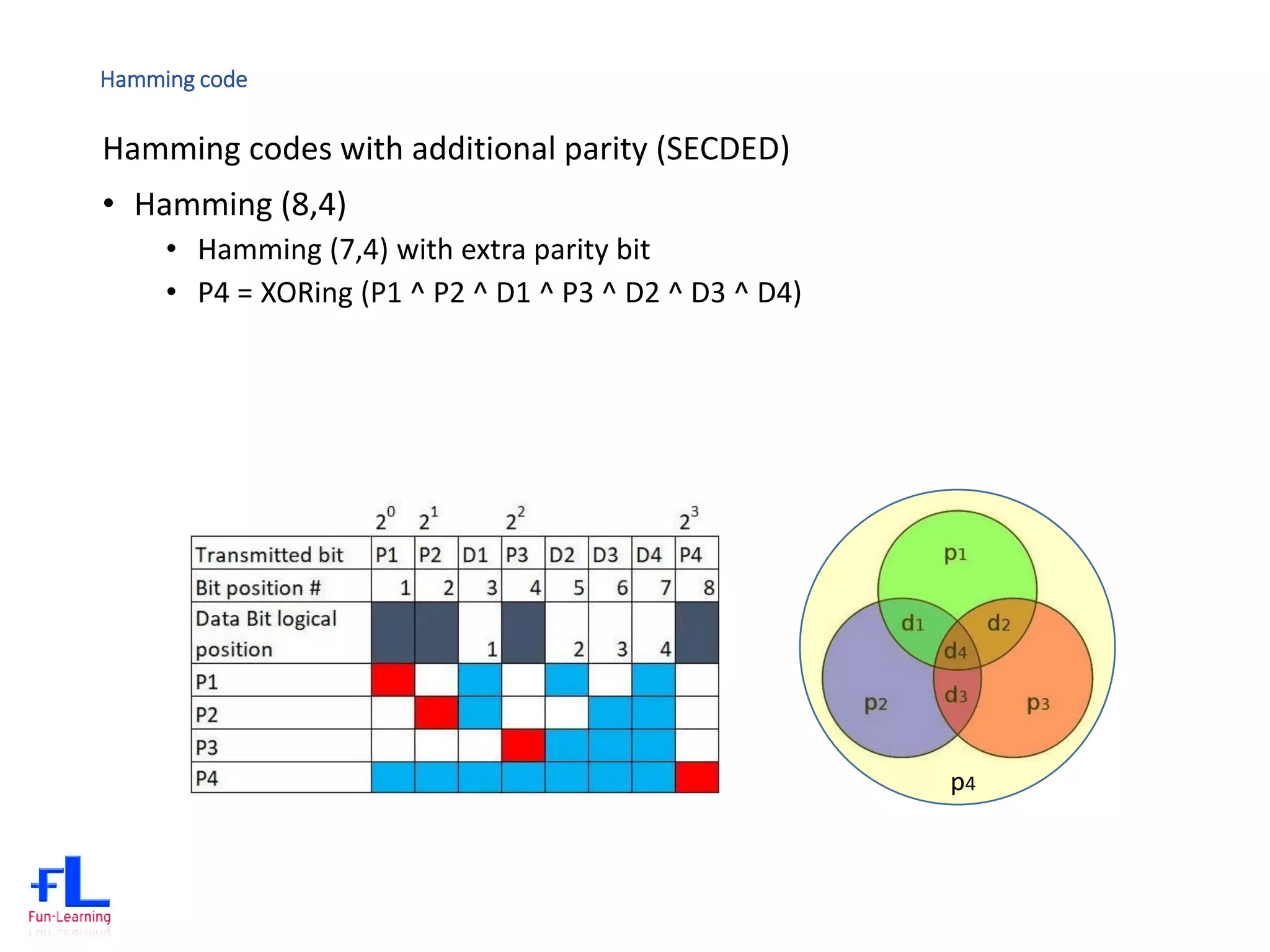
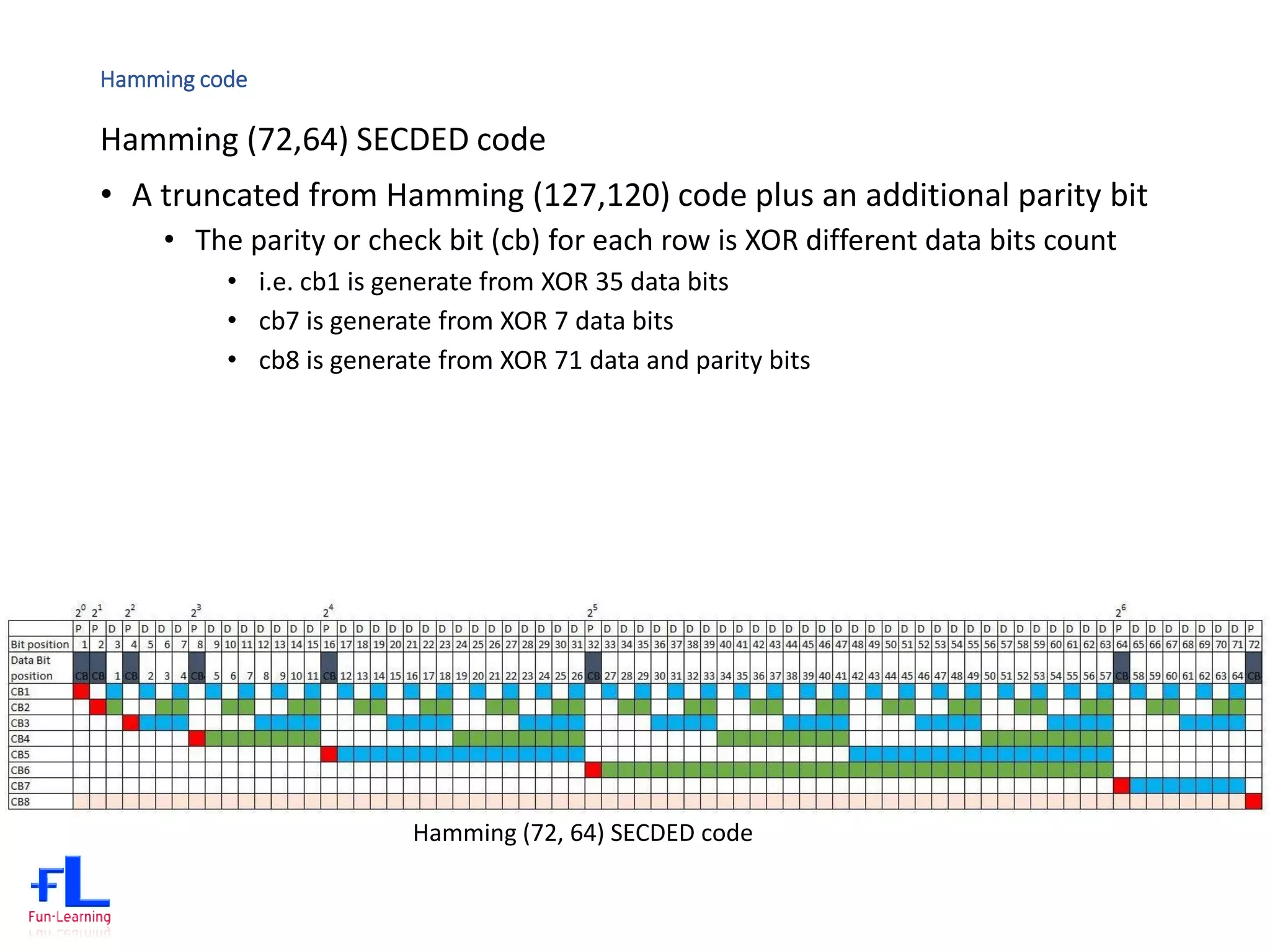
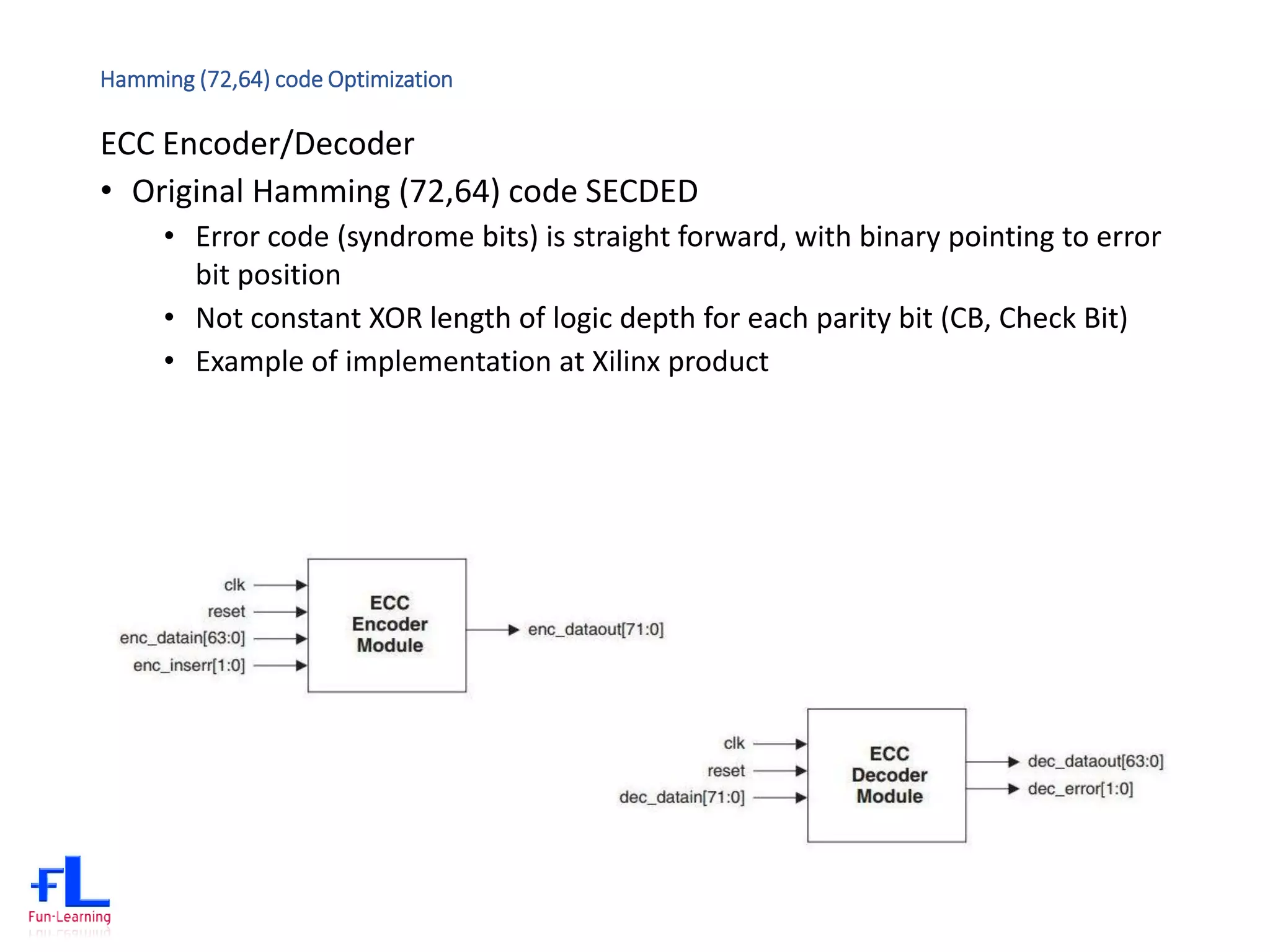
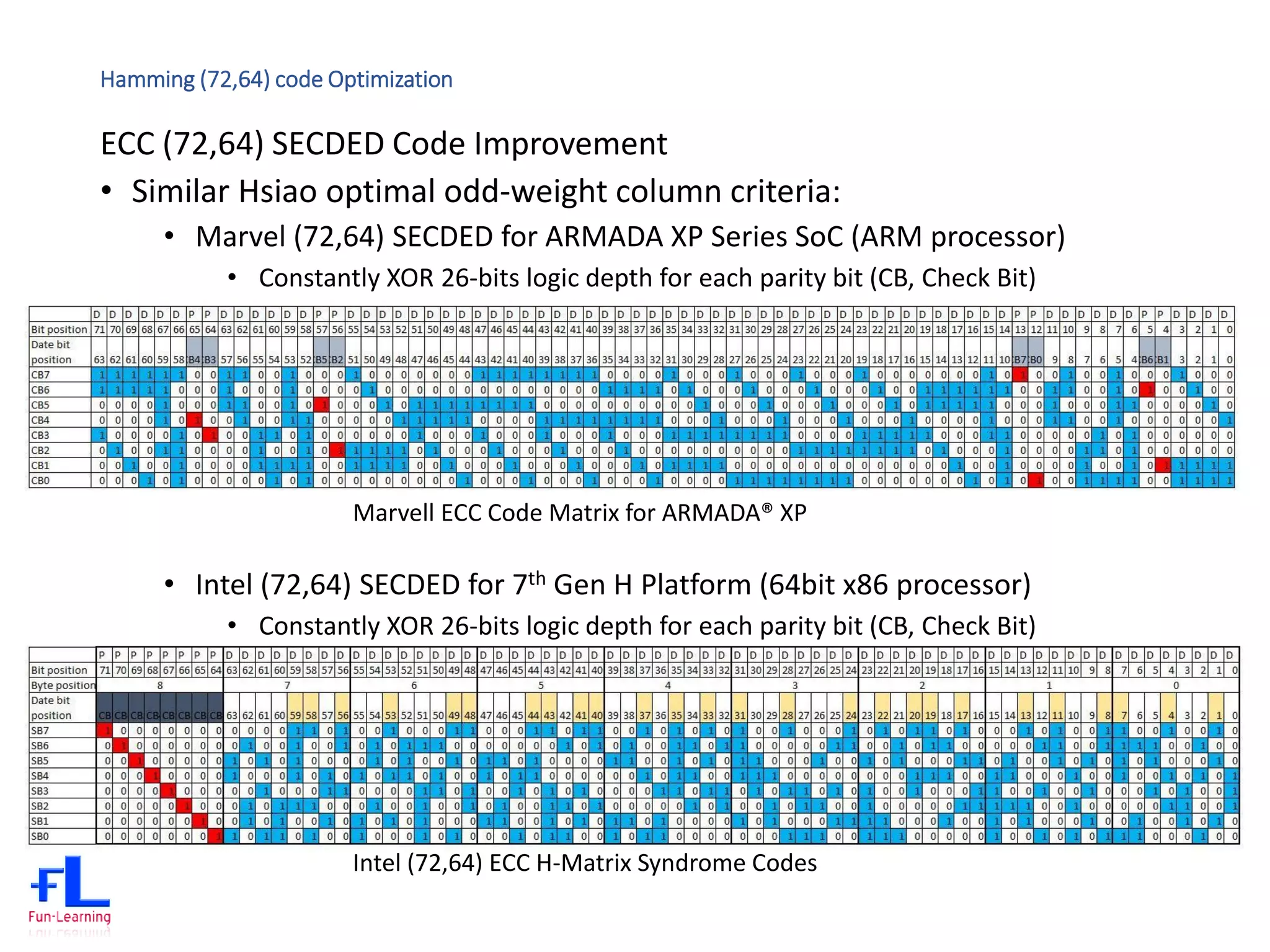
The document discusses error correction codes (ECC) used for dynamic random access memory (DRAM). It introduces how ECC is implemented using a memory controller on the processor. It describes the academic background of Hamming codes, including the commonly used (72,64) single error correction, double error detection (SECDED) code. It also discusses optimizations of the (72,64) SECDED code implemented in industrial systems to simplify the logic and reduce gate counts.

1. Mechanism Insight: Memory ECC -
The Comprehensive of SEC-DED
Close the gaps between academic and industrial practice.

2. Processor - Memory ECC
Academic:
• Introduction of Memory Controller (processor) ECC for DRAM
• Hamming code
• M.Y. Hsiao (72,64) SECDED Code “Optimal Minimum Odd-weight-
column”
• ECC Encoder/Decoder
Industrial 64+ECC Implementation:
• Xilinx unmodified Hamming code
• Lattice ECC module with Hsiao-Code
• Intel Gen 7th Processor DDR4 ECC
• Marvell Multi-Core ARMv7 Based SOC Processor DDR3 ECC
• Multiple-bits failure and manually decode

3. Processor - Memory ECC
Where is bit flipped error occur?
• Inside memory controller
• SEU (Single Event Upset)
• Circuitry signal
• IC component - DRAM
• DRAM cell
• DRAM SEU (Single Event Upset)
• DRAM Fault

4. Academic:
Introduction of Memory Controller
(processor) ECC for DRAM

5. Introduction of Memory Controller (processor) ECC for DRAM
Background of ECC (Error Correction Code) for DRAM
• DRAM (Dynamic Random Access Memory)
• Error Detection and Correction (EDAC)
Memory modules with
Error Correction Code (ECC)
Legacy memory modules
DIMM
Register
Memory
Controller
DIMM
Register
Data
Data
CMD/
ADDR/CLK
DIMM
Register
Memory
Controller
DIMM
Register
Data
Data
CMD/
ADDR/CLK
Check Bit
ECC
mechanism

6. Introduction of Memory Controller (processor) ECC for DRAM
ECC Memory
10010101
01001011
00110101
11010110
10010101
01001011
00110101
11010110
10010101
01001011
00110101
11010110
10010101
01001011
00110101
11010110
10010101
01001011
00110101
11010110
10010101
01001011
00110101
11010110
10010101
01001011
00110101
11010110
10010101
01001011
00110101
11010110
10010101
01001011
00110101
11010110
10010101
01001011
00110101
11010110
10010101
01001011
00110101
11010110
10010101
01001011
00110101
11010110
10010101
01001011
00110101
11010110
10010101
01001011
00110101
11010110
10010101
01001011
00110101
11010110
10010101
01001011
00110101
11010110
10010101
01001011
00110101
11010110
10010101
01001011
00110101
11010110
8-bits 8-bits 8-bits 8-bits 8-bits 8-bits 8-bits 8-bits 8-bits
64-bits ECC

7. Introduction of Memory Controller (processor) ECC for DRAM
Introduction of Memory Controller ECC Implementation
• Hamming code - Single-bit Error Correction, Double-bit Error Detection
(SECDED)
• 32-bit Processor
• 32-bit memory + ECC is commonly using (39,32) SECDED Code
• 64-bit Processor
• 64-bit memory + ECC is commonly using (72,64) SECDED Code
• 32-bit compatible mode – mostly half 32-bit set to zero, either high-32 or
low-32
• 9 chips DDR3 DIMM
• Each DRAM ICs has 8-bit data width, so a total of 64 data bits will be
transferred. It is 4GB (512MBx8) configuration.
• In addition, the extra ECC chip will output another 8 bits, making the module
72-bit wide

8. Introduction of Memory Controller (processor) ECC for DRAM
Endianness
• How the 32-bit or 64-bit hex value stored in memory?
• Big Endian vs Little Endian
• Least Significant Byte (LSB) – smallest quantity or weight byte
• Most Significant Byte (MSB) – largest quantity or weight byte
• Least Significant Bit (LSb) – smallest quantity or weight bit
• Most Significant Bit (MSb) – largest quantity or weight bit
• Bi-endian processors
• Operate in either little-endian or big-endian
mode

9. Academic:
Hamming code

10. Hamming code
History of Hamming code
• Hamming (7,4) code used in telecommunication
• Invented by Richard W. Hamming in 1950, during work at Bell Telephone
Laboratories
• Encodes four bits of data into seven bits by adding three parity bits
• Detect and correct any single-bit error

11. Hamming code
Hamming codes algorithm
• The general algorithm generates a single-error correcting (SEC) code for
any number of bits
1) Arrange bits position starting from 1: bit 1, 2, 3, 4, 5, etc.
2) All bit positions powers of two (2n) are parity bits
3) All other bit positions are data bits in sequence
4) Each data bit is covers with parity bits of its binary form position.
• m parity bits, cover bits from 1 up to 2m − 1. i.e. Hamming (31,26)

12. Hamming code
Hamming codes algorithm
• Generate parity bits for Hamming(31,26) code
• P1 = XORing (D1 ^ D2 ^ D4 ^ D5 ^ D7 ^ D9 ^ D11 ^ D12 ^ D14 ^ D16 ^ D18 ^
D20 ^ D22 ^ D24 ^ D26)
• P2 = XORing (D1 ^ D3 ^ D4 ^ D6 ^ D7 ^ D10 ^ D11 ^ D13 ^ D14 ^ D17 ^ D18
^ D21 ^ D22 ^ D25 ^ D26)
• So on

13. Hamming code
Hamming codes Single-bit Error Correction (SEC)
• Calculate syndrome bits
• Sb1 = XORing (P1 ^ D1 ^ D2 ^ D4 ^ D5 ^ D7 ^ D9 ^ D11 ^ D12 ^ D14 ^ D16 ^
D18 ^ D20 ^ D22 ^ D24 ^ D26)
• Sb2 = XORing (P2 ^ D1 ^ D3 ^ D4 ^ D6 ^ D7 ^ D10 ^ D11 ^ D13 ^ D14 ^ D17
^ D18 ^ D21 ^ D22 ^ D25 ^ D26)
• So on
• Binary syndrome bits (sb5,sb4,sb3,sb2,sb1) tells the bit fault position
• i.e bin (sb5,sb4,sb3,sb2,sb1) = 00110 = bit position 6 flipped

14. Hamming code
Hamming codes
• The possible Hamming codes
• m parity bits, cover bits from 1 up to 2m − 1.
• ECC Algorithm
• Uses Hamming (72,64) code SECDED algorithm
• A truncated from Hamming (127,120) code plus an additional parity bit,
which has the same space overhead as a (9,8) parity code

15. Hamming code
Hamming codes with additional parity (SECDED)
• Basic concept of parity check (9,8)
• Encode for parity bit:
• Parity generate by XOR 8-bits logic depth
• Decode (parity check):
• Total 9 bits are XORing to obtain result: Even (0) is no error; Odd (1) is found
error
• Double-bit error detection for Hamming (31,26) code
• Add extra parity bit to calculate all 31 bits from Hamming(31,26) code
• Hamming (32,26) code is SECDED
Traditional XOR Symbol IEEE XOR Symbol

16. Hamming codes with additional parity (SECDED)
• Hamming (8,4)
• Hamming (7,4) with extra parity bit
• P4 = XORing (P1 ^ P2 ^ D1 ^ P3 ^ D2 ^ D3 ^ D4)
Hamming code
p4

17. Hamming code
Hamming (72,64) SECDED code
• A truncated from Hamming (127,120) code plus an additional parity bit
• The parity or check bit (cb) for each row is XOR different data bits count
• i.e. cb1 is generate from XOR 35 data bits
• cb7 is generate from XOR 7 data bits
• cb8 is generate from XOR 71 data and parity bits
Hamming (72, 64) SECDED code

18. Academic:
Hamming (72,64) code Optimization

19. Hamming (72,64) code Optimization
ECC Encoder/Decoder
• Original Hamming (72,64) code SECDED
• Error code (syndrome bits) is straight forward, with binary pointing to error
bit position
• Not constant XOR length of logic depth for each parity bit (CB, Check Bit)
• Example of implementation at Xilinx product

20. ECC (72,64) SECDED Code Improvement
• (72,64) SECDED by M. Y. Hsiao (1970)
• Constantly XOR 26-bits logic depth for each parity bit (CB, Check Bit)
• Simpler to implement at silicon with reduce gates count
• Example of implementation at Lattice product
• The constructing optimal odd-weight column criteria (ref. 1):
1) There are no all-0 columns (or all-1 columns)
2) Every column is distinct
3) Every column contains an odd number of 1's (here odd weight)
• The columns used odd-weight 3 or 5 of 1's, and no odd-weight of 7
Hsiao Parity-check matrix of the (72, 64) SECDED code, version 1
Hamming (72,64) code Optimization

21. ECC (72,64) SECDED Code Improvement
• Similar Hsiao optimal odd-weight column criteria:
• Marvel (72,64) SECDED for ARMADA XP Series SoC (ARM processor)
• Constantly XOR 26-bits logic depth for each parity bit (CB, Check Bit)
• Intel (72,64) SECDED for 7th Gen H Platform (64bit x86 processor)
• Constantly XOR 26-bits logic depth for each parity bit (CB, Check Bit)
Intel (72,64) ECC H-Matrix Syndrome Codes
Marvell ECC Code Matrix for ARMADA® XP
Hamming (72,64) code Optimization