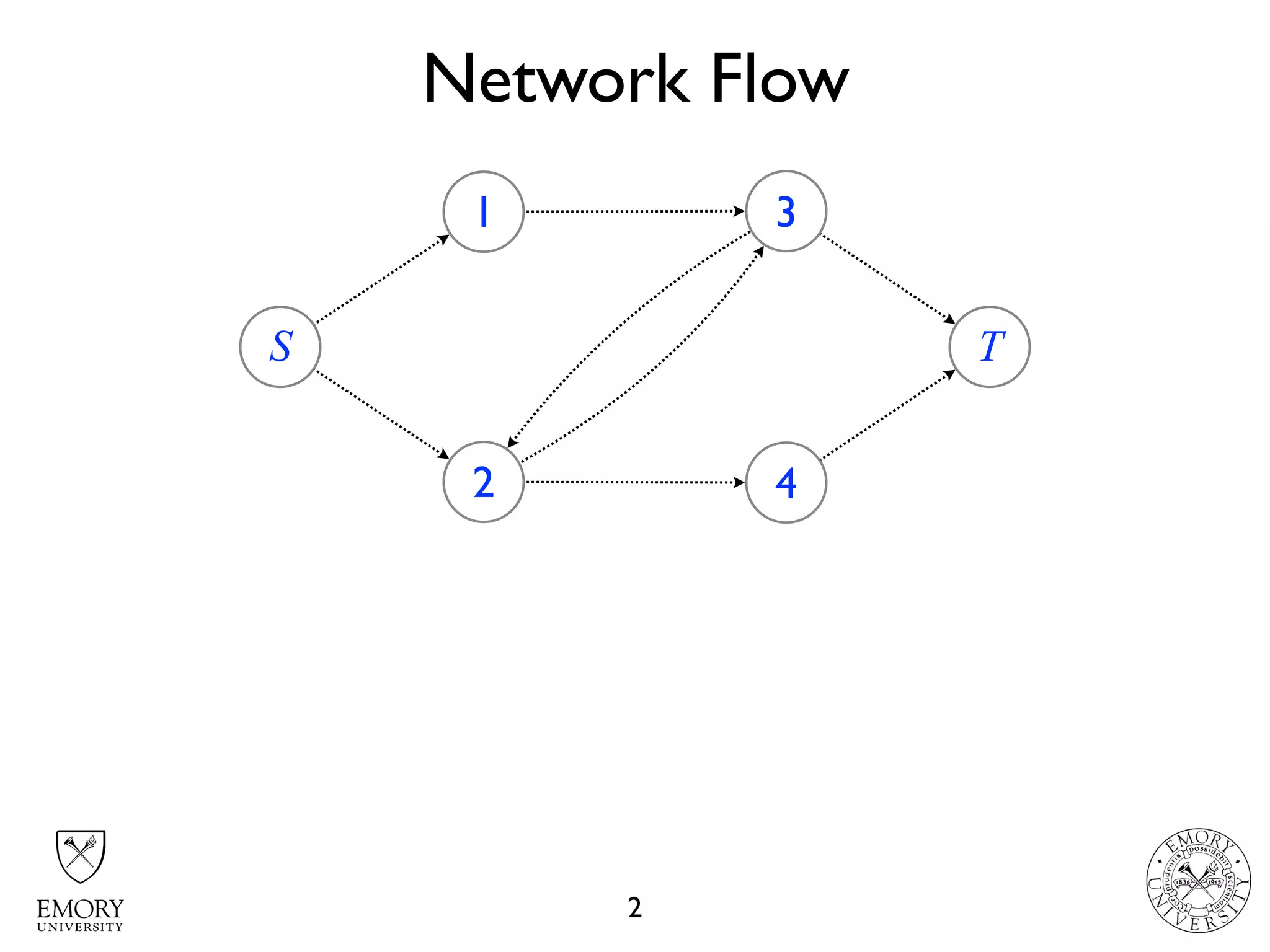
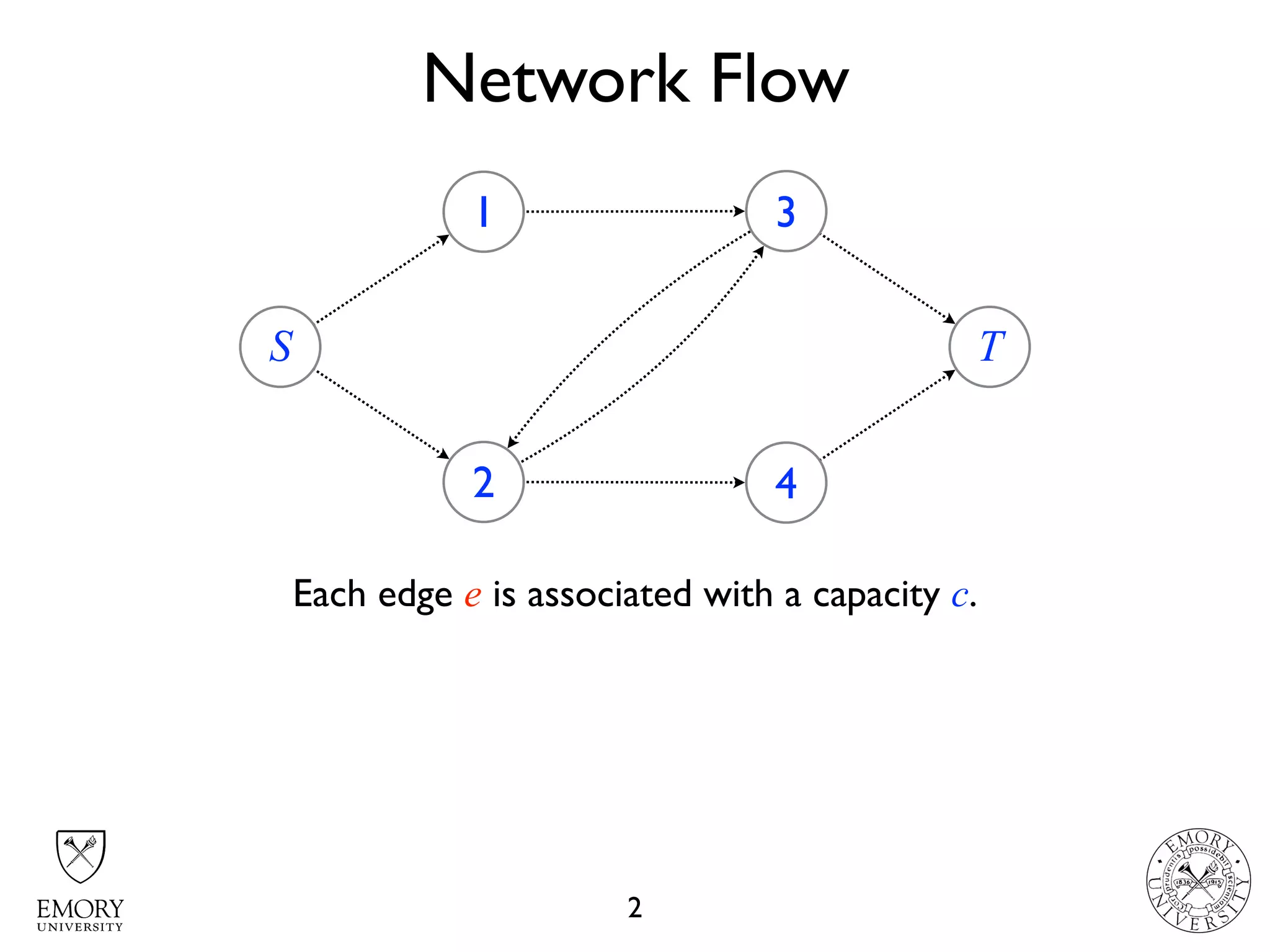
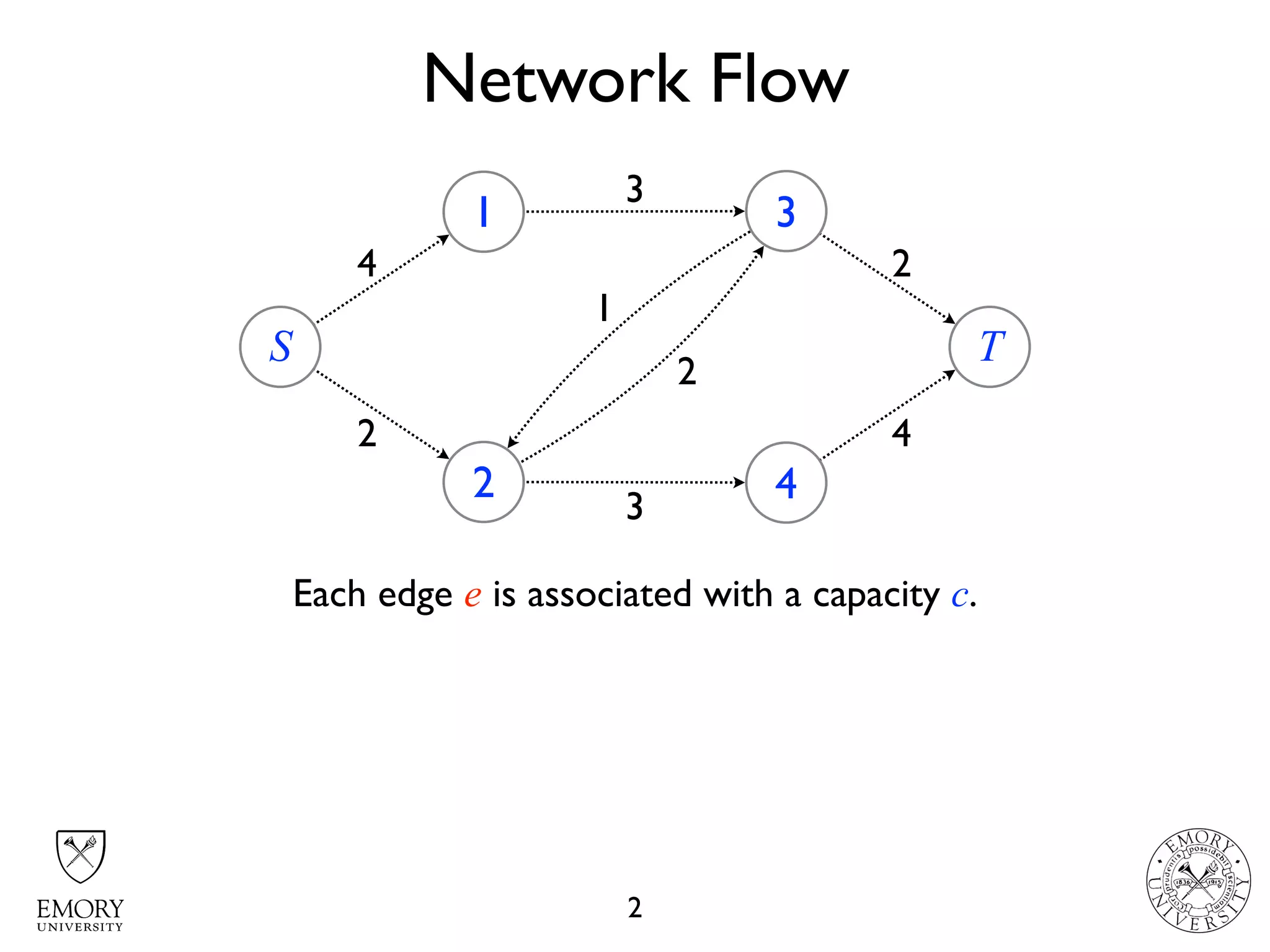
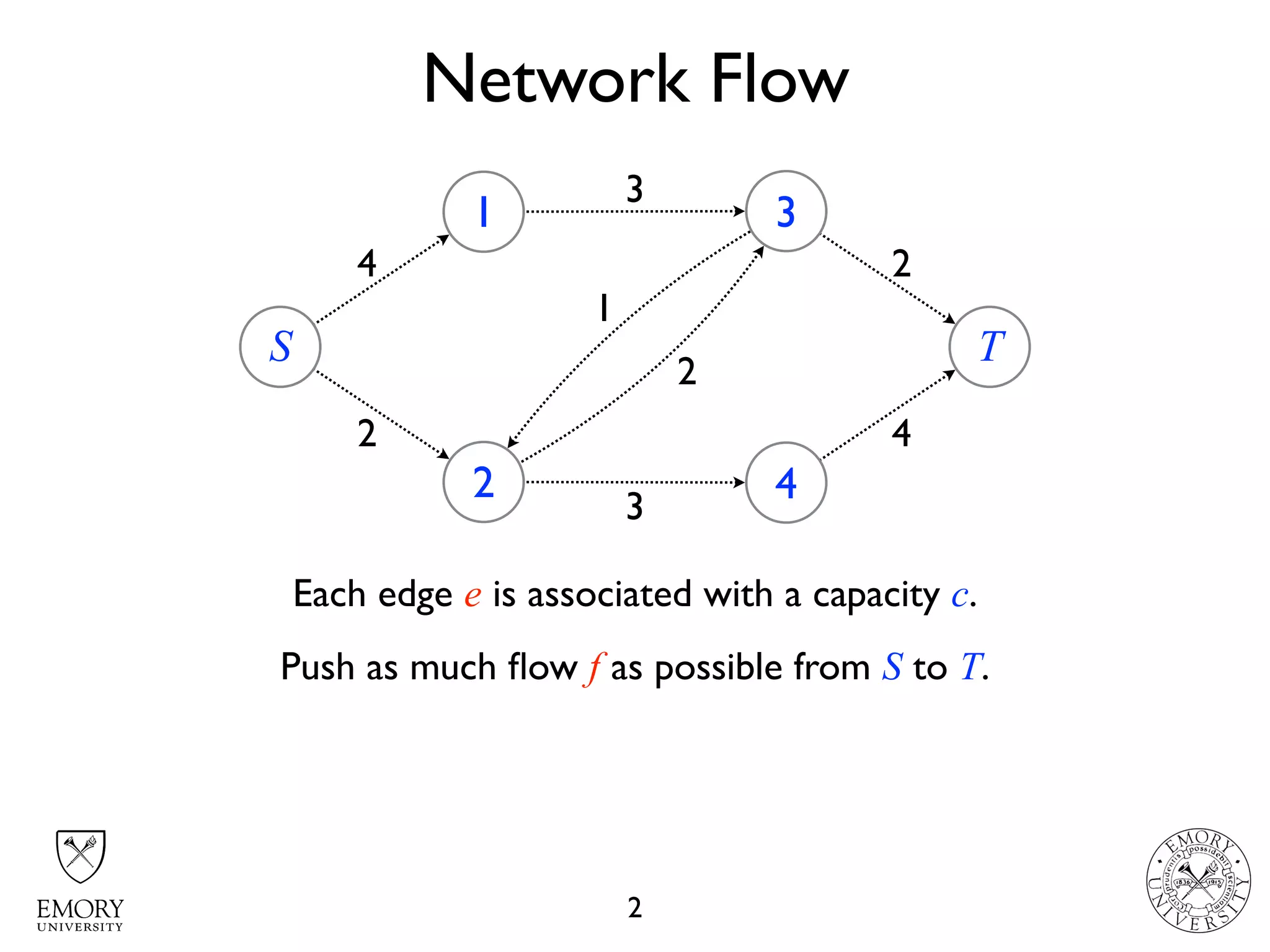
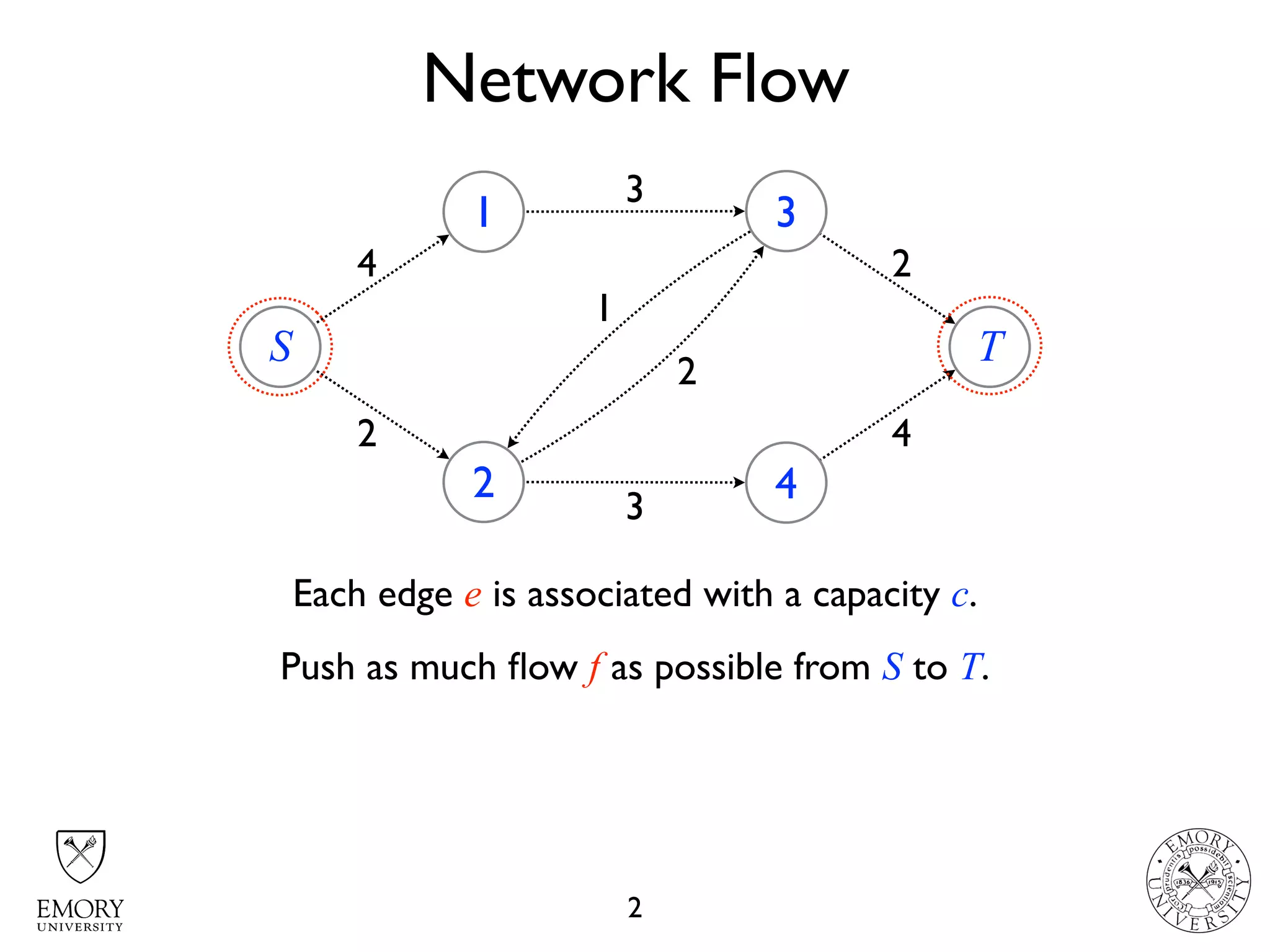
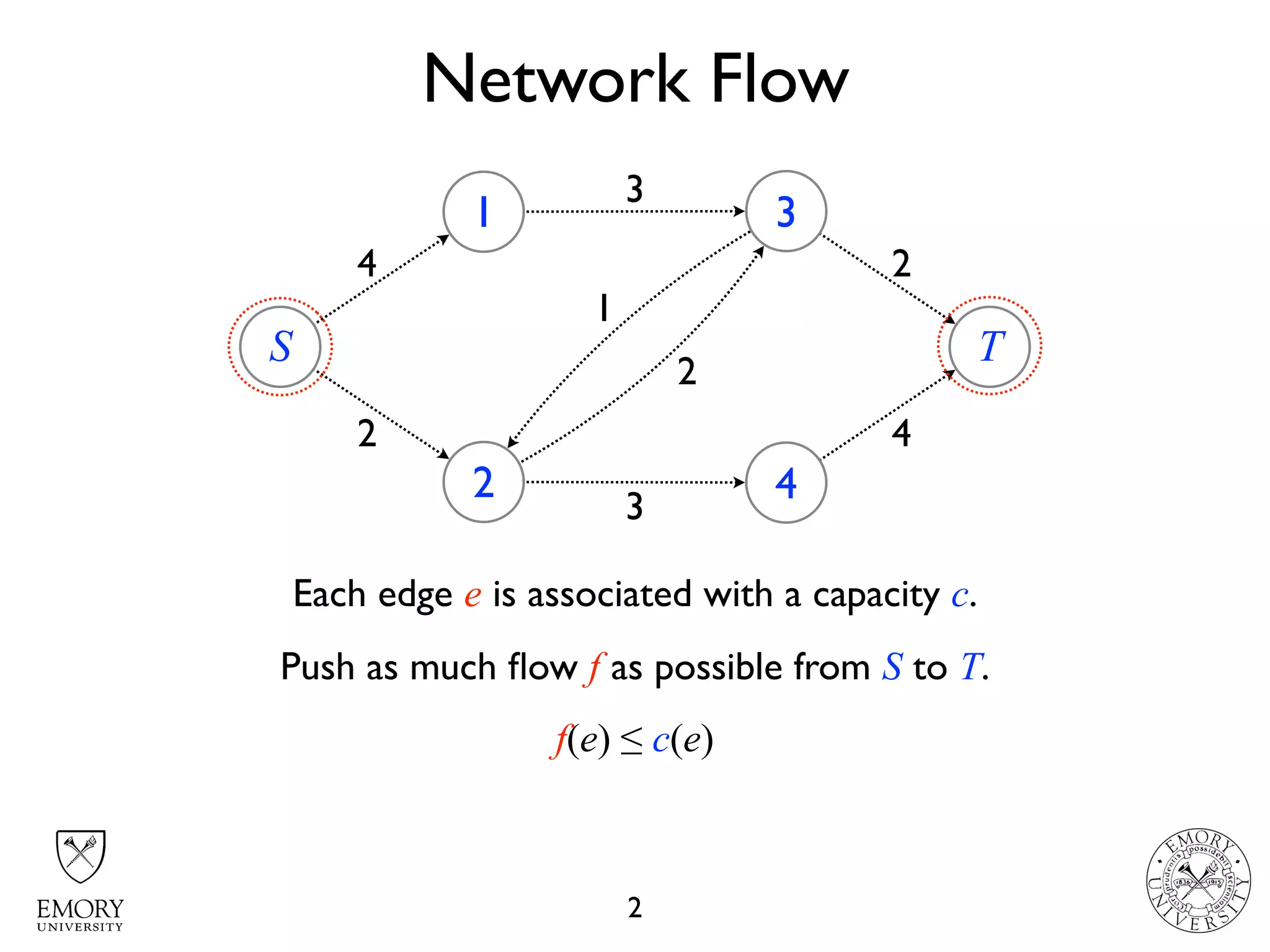
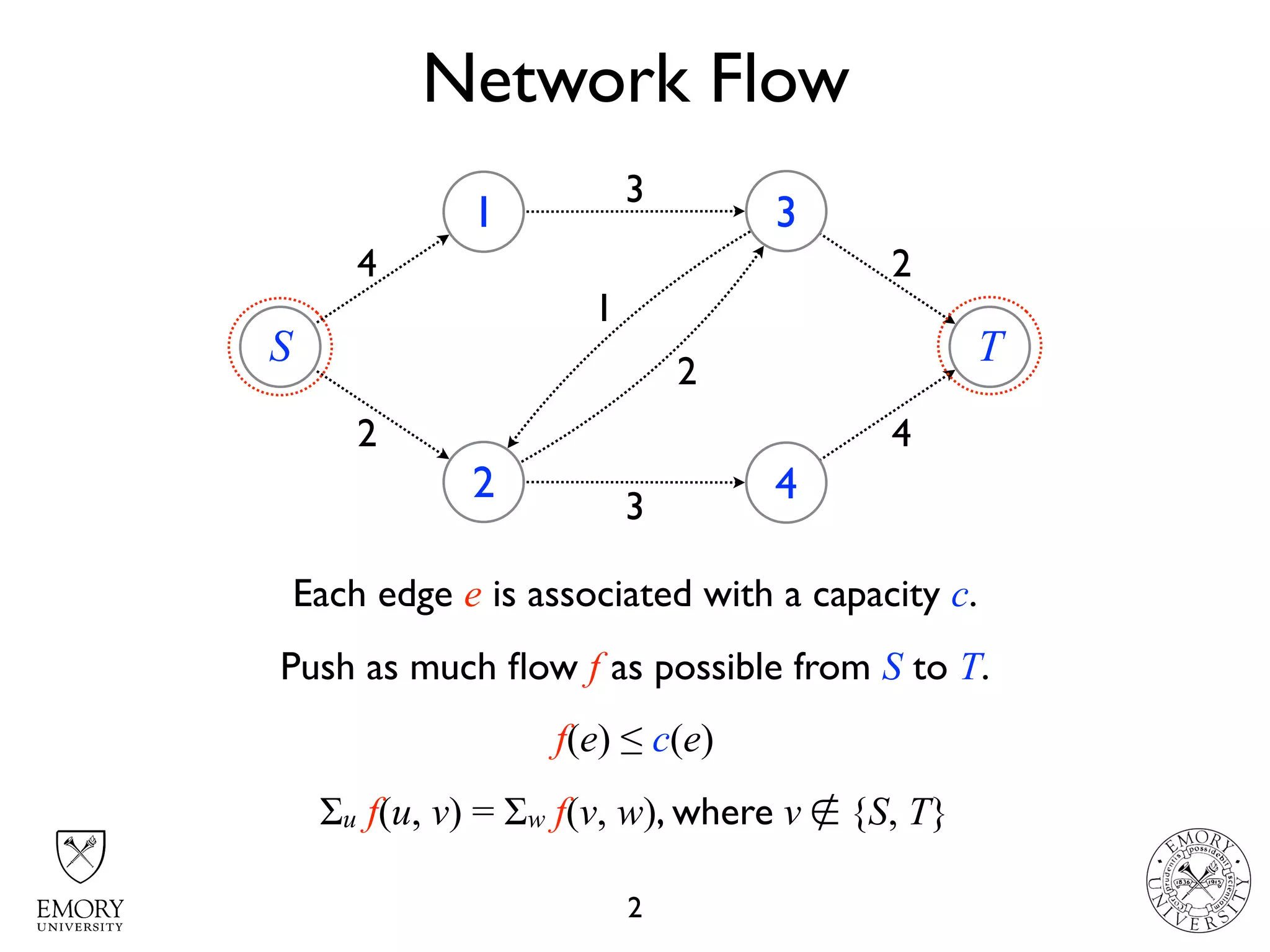
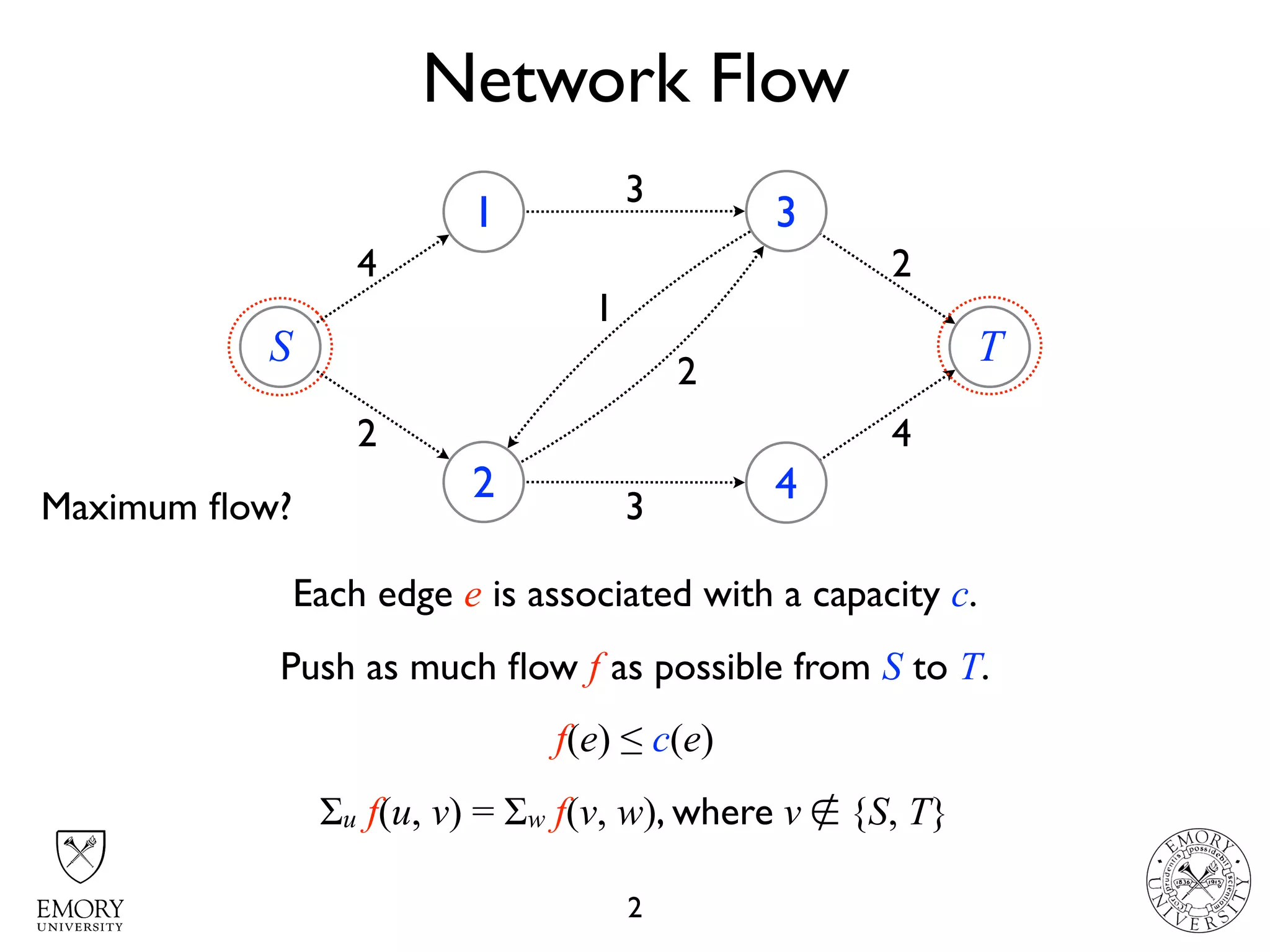
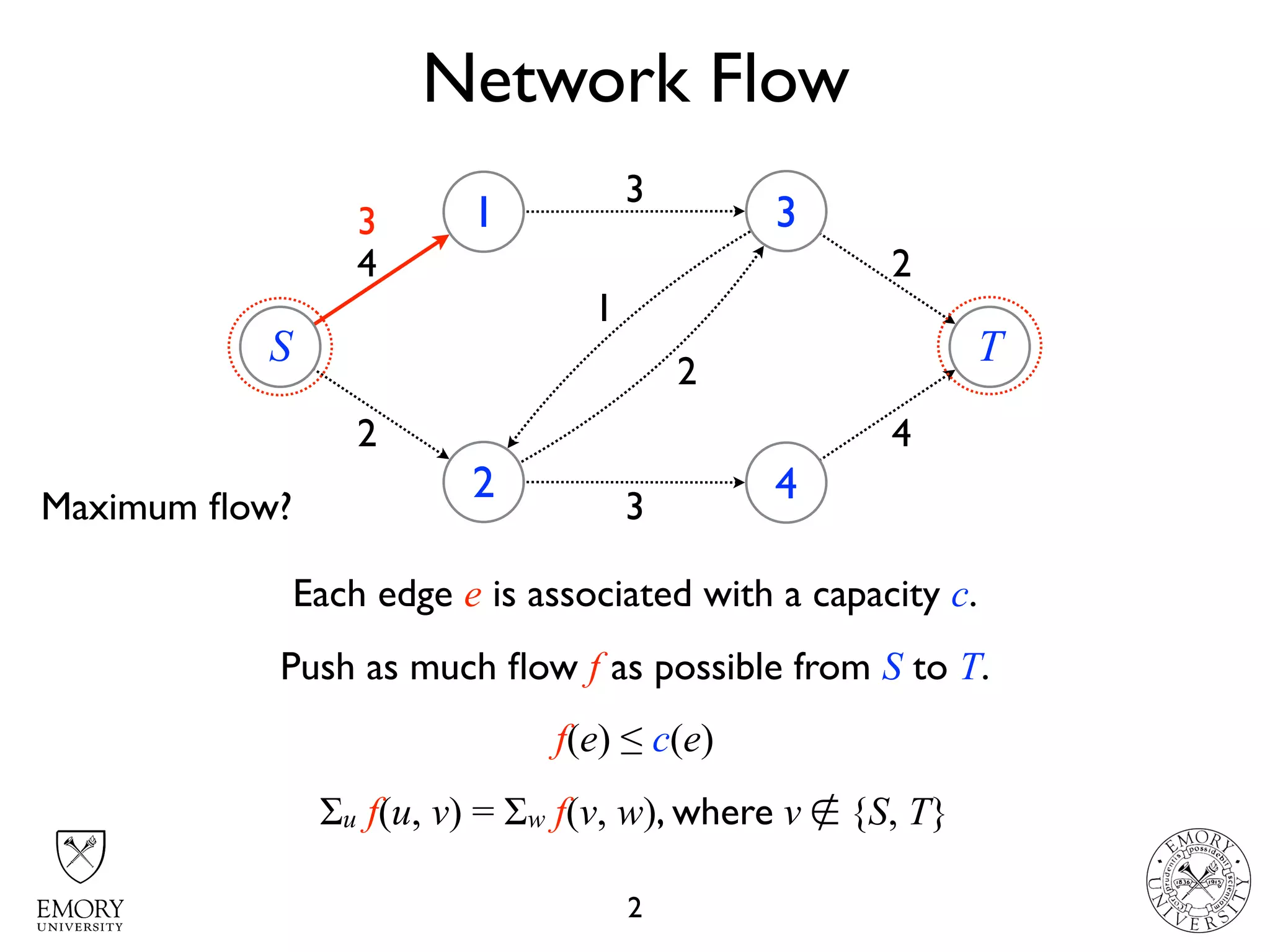
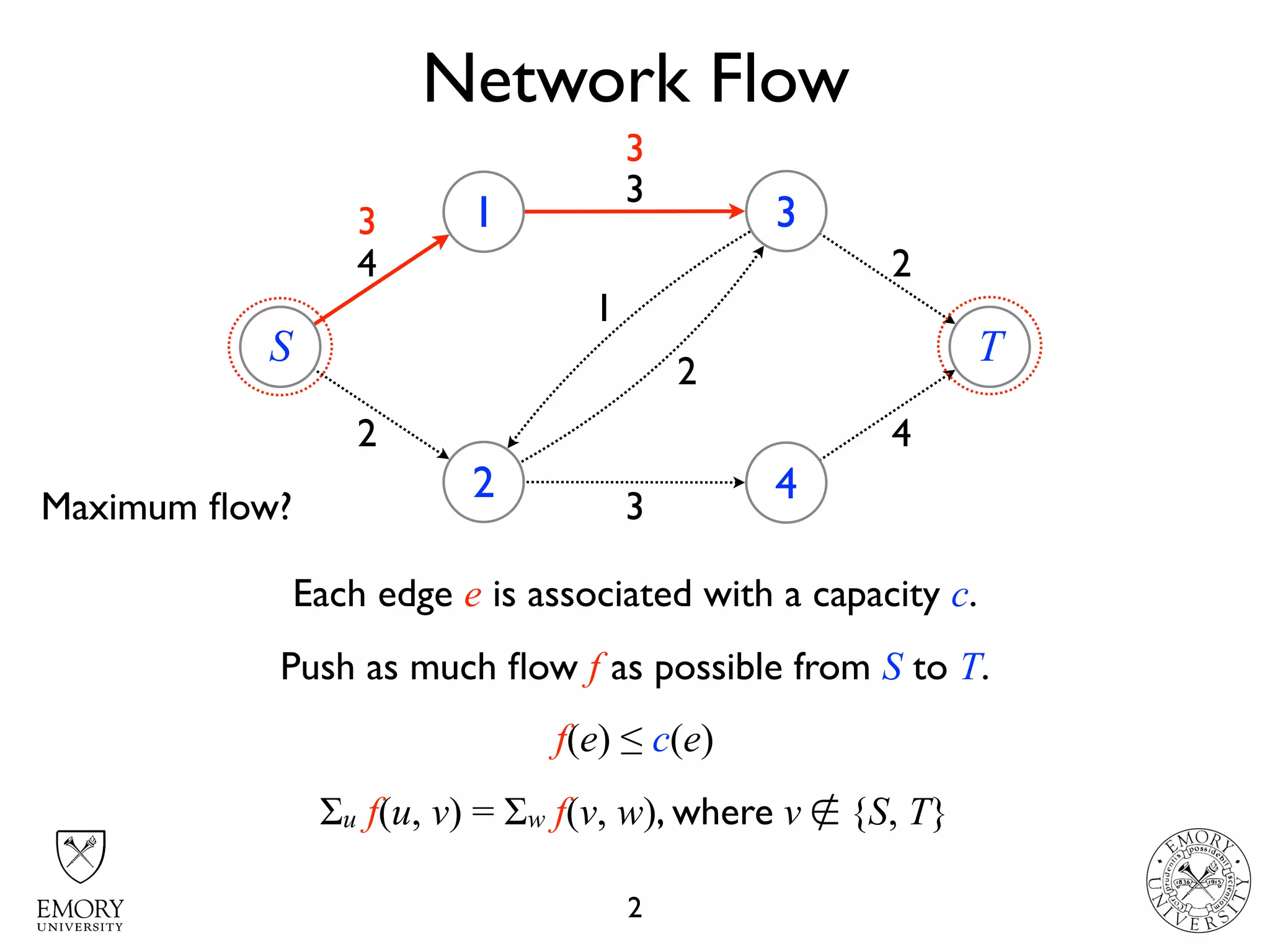
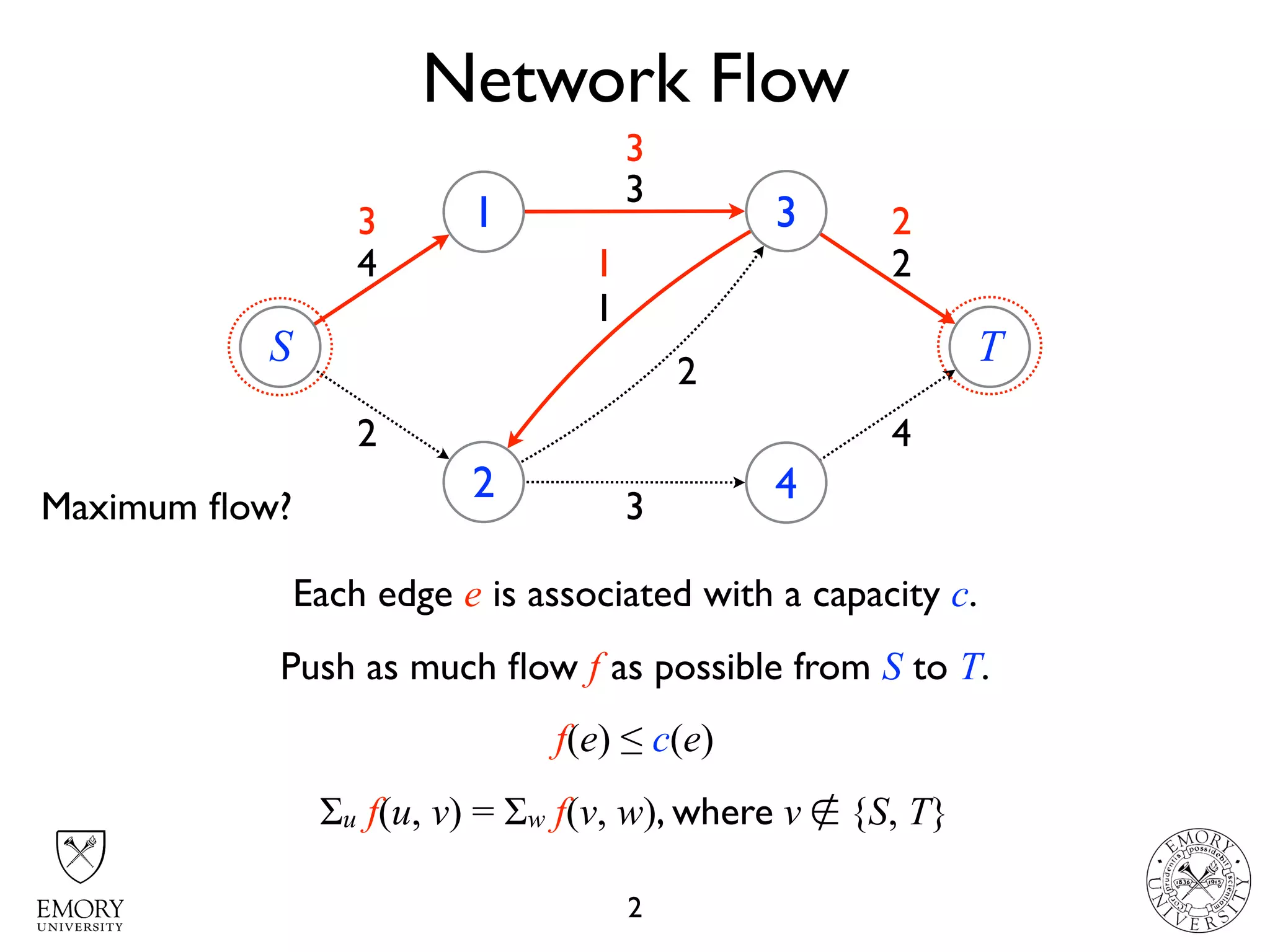
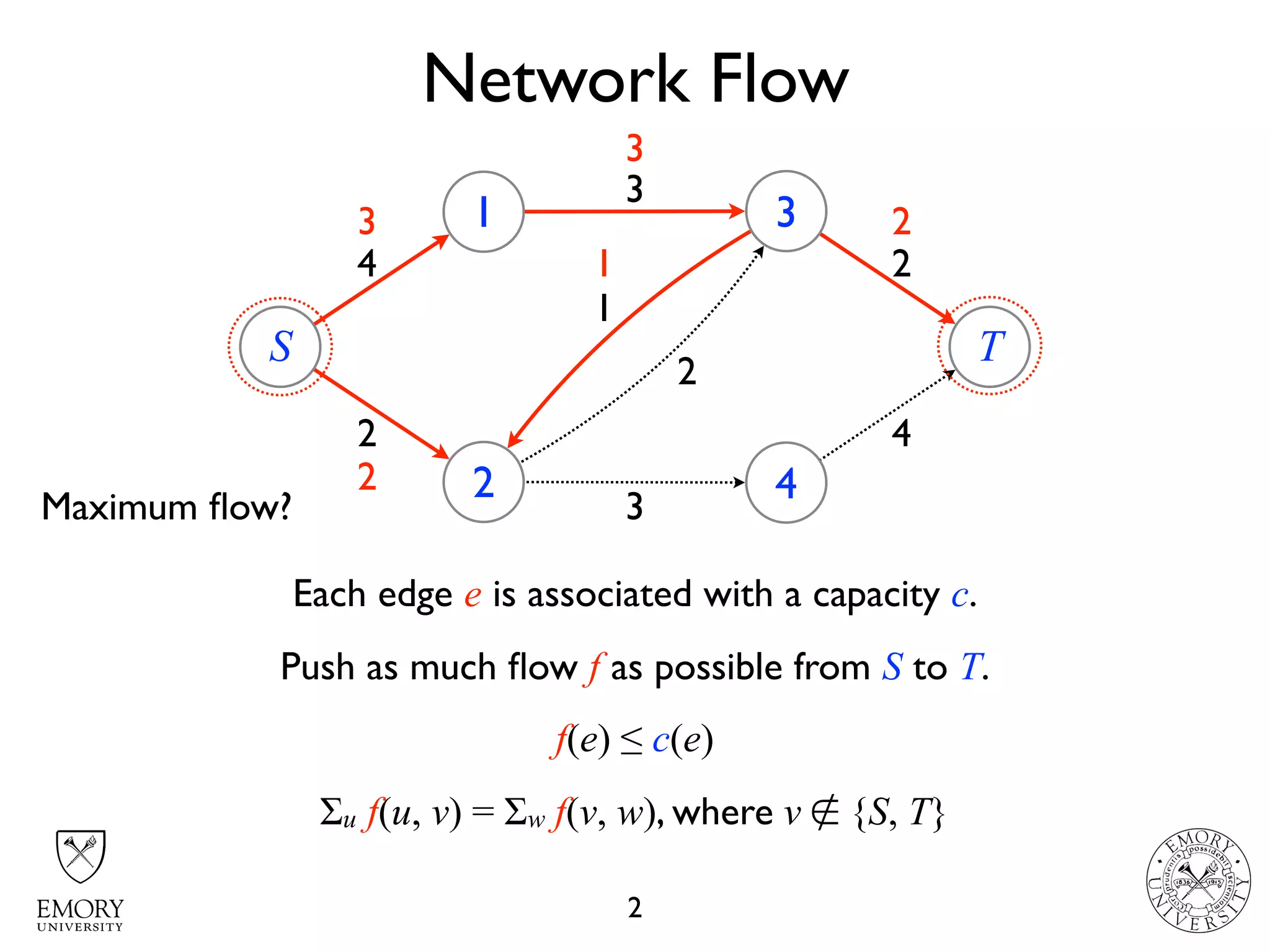
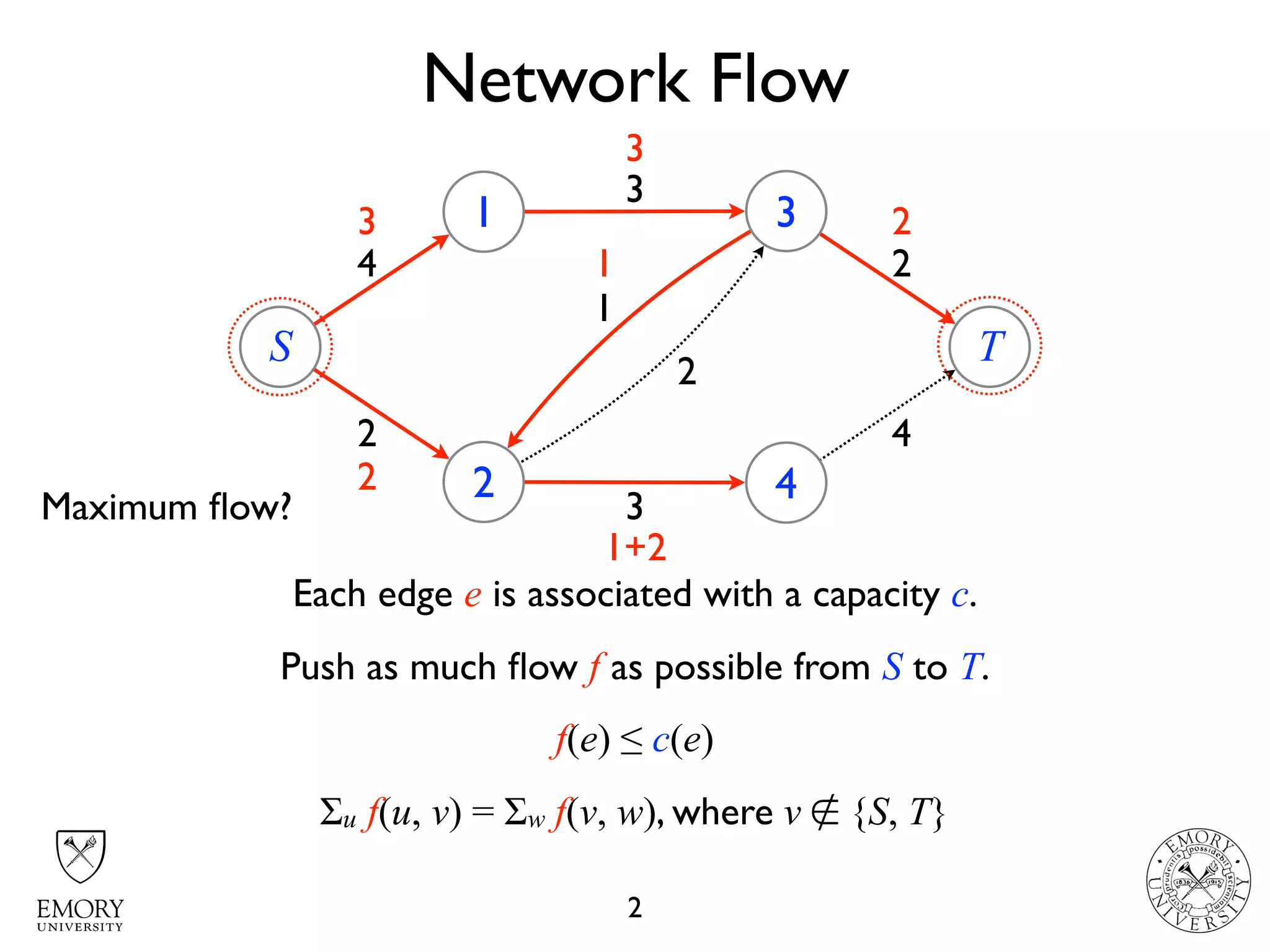
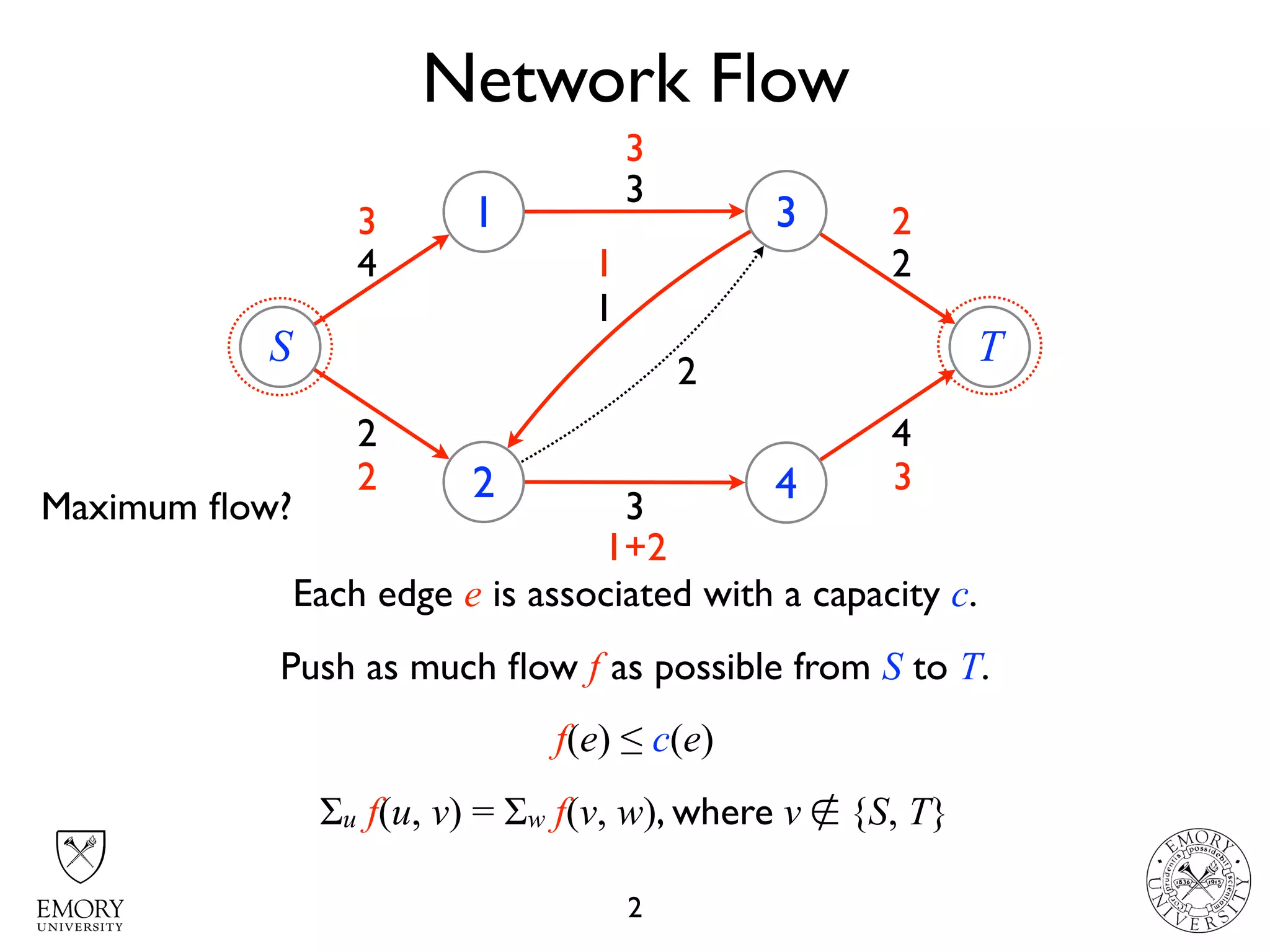
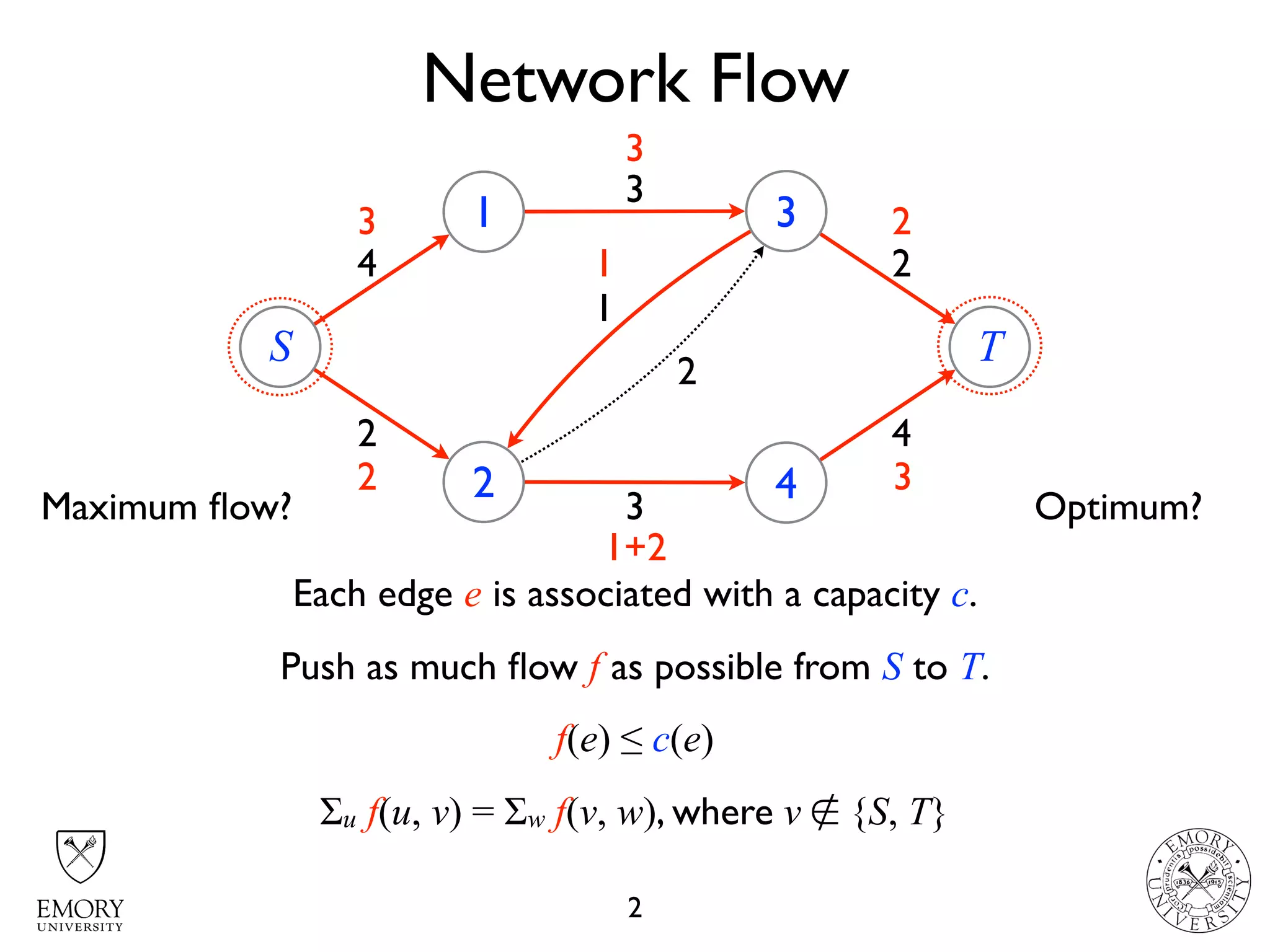
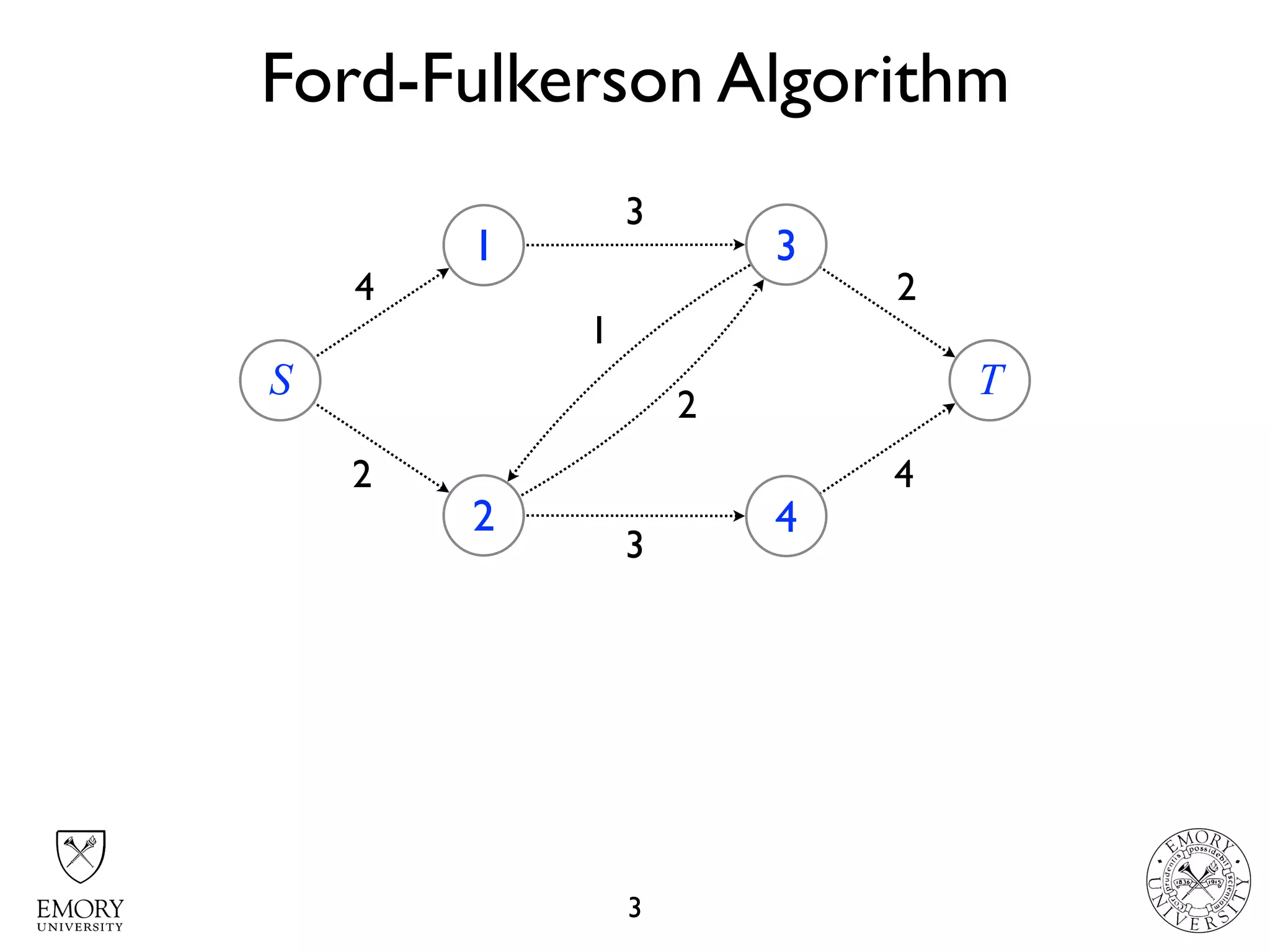
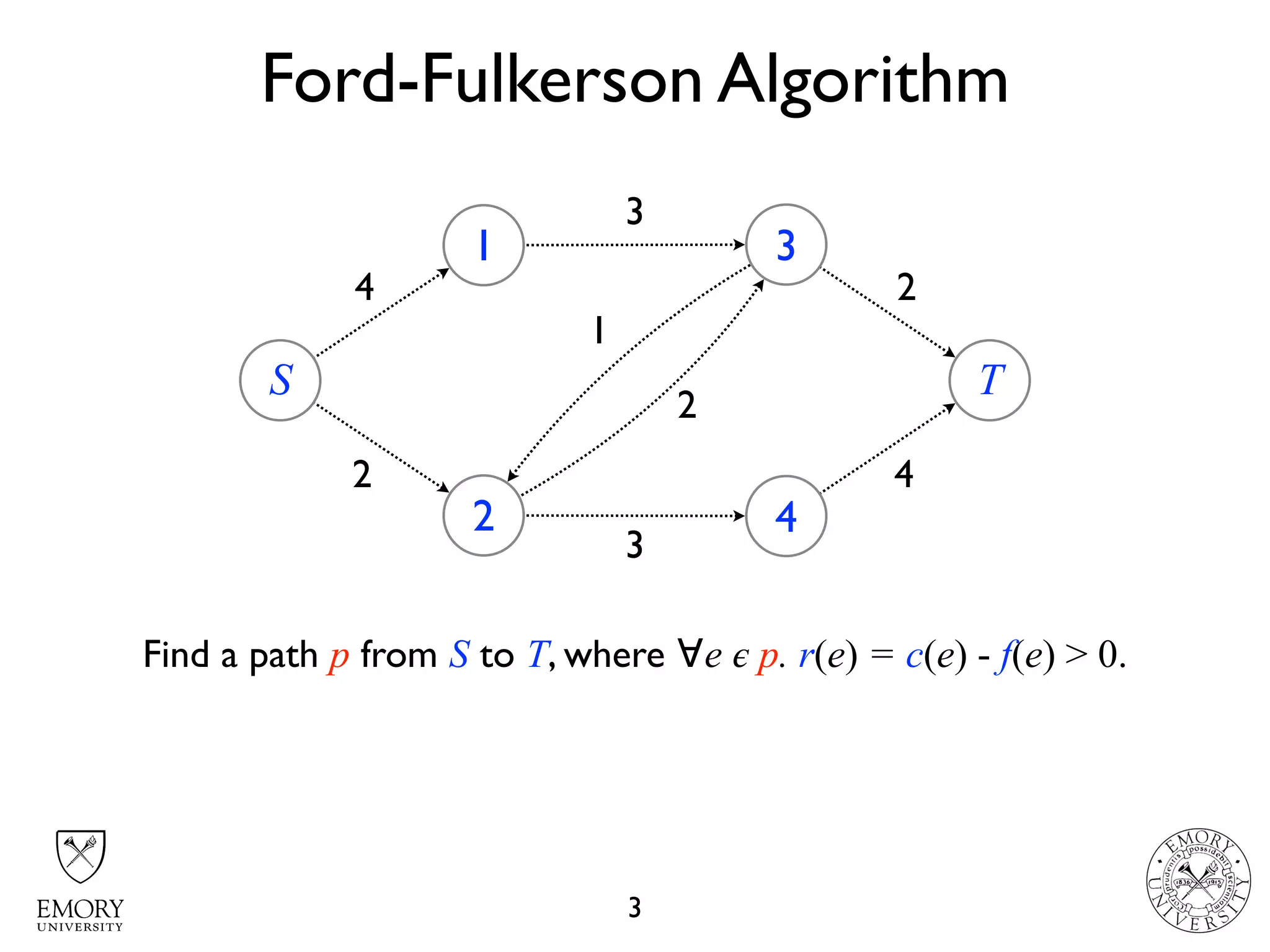
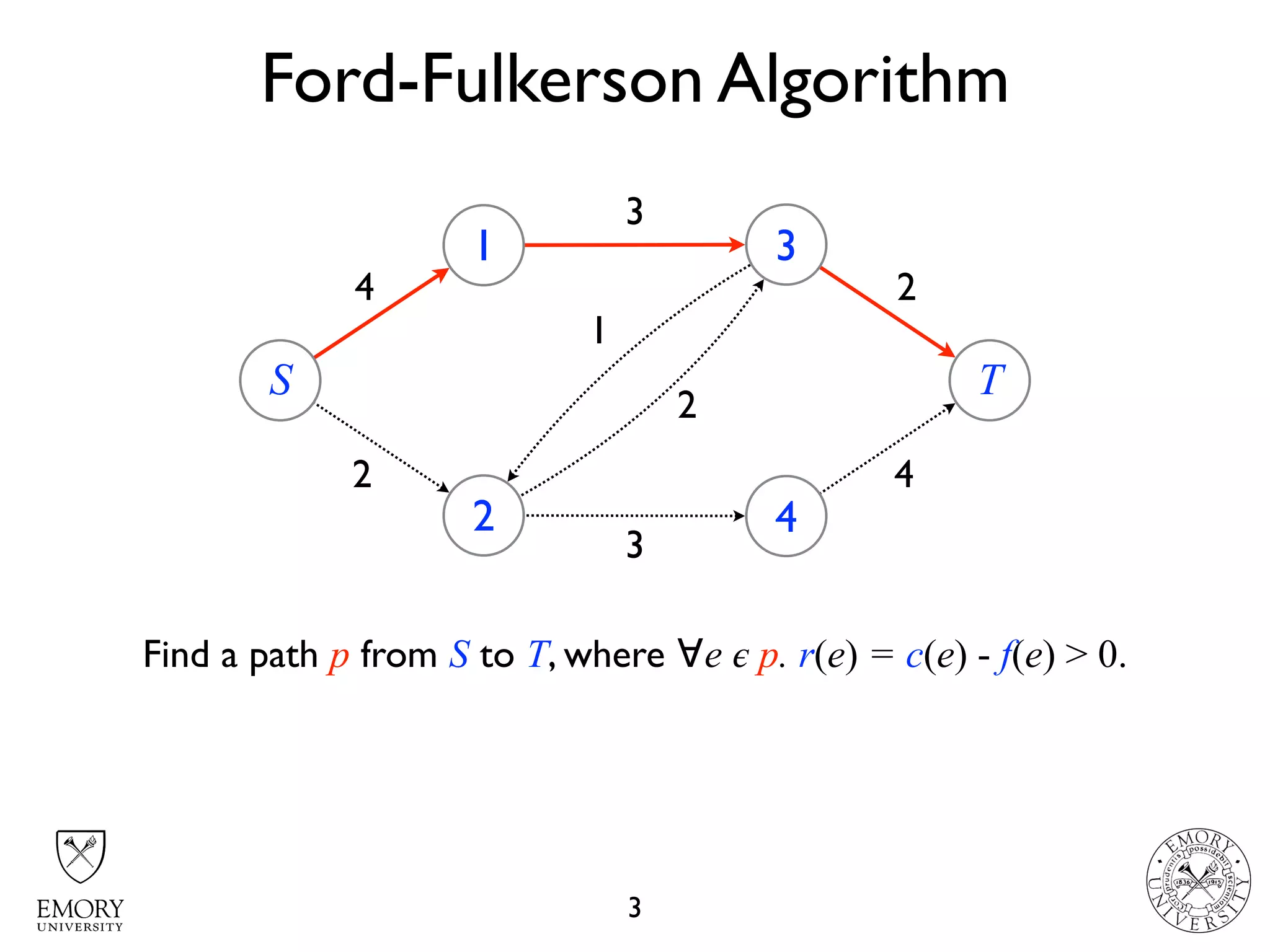
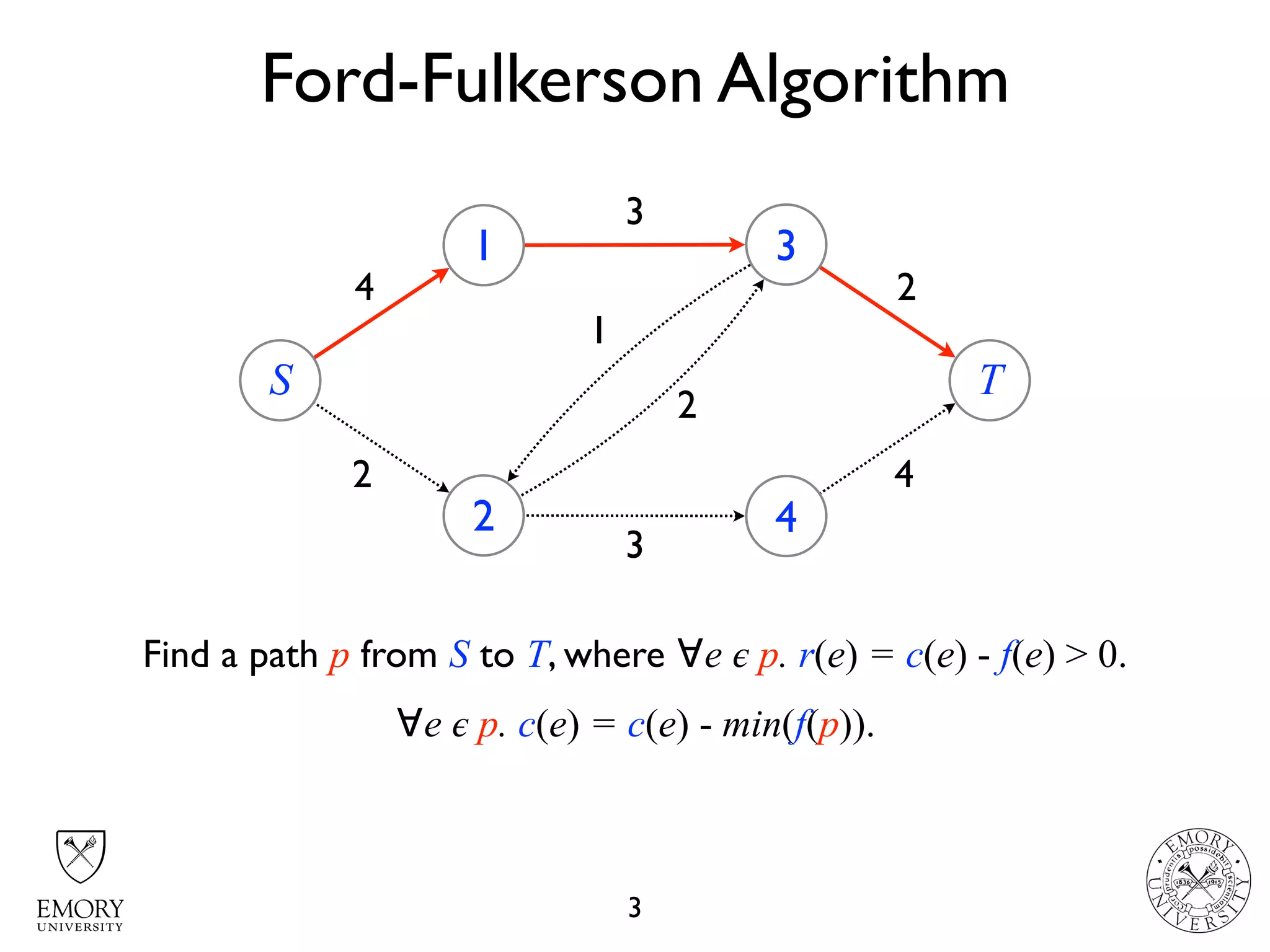
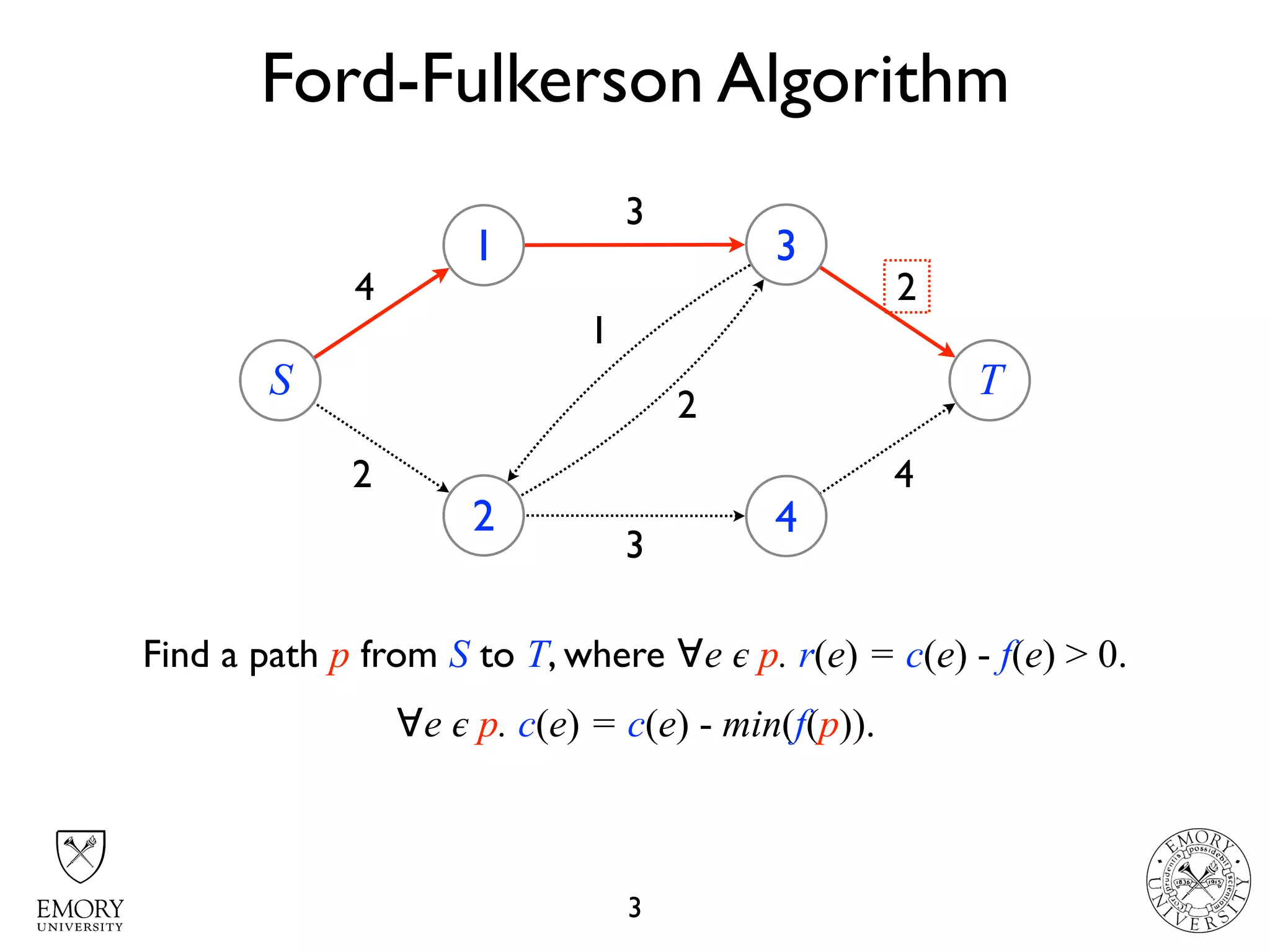
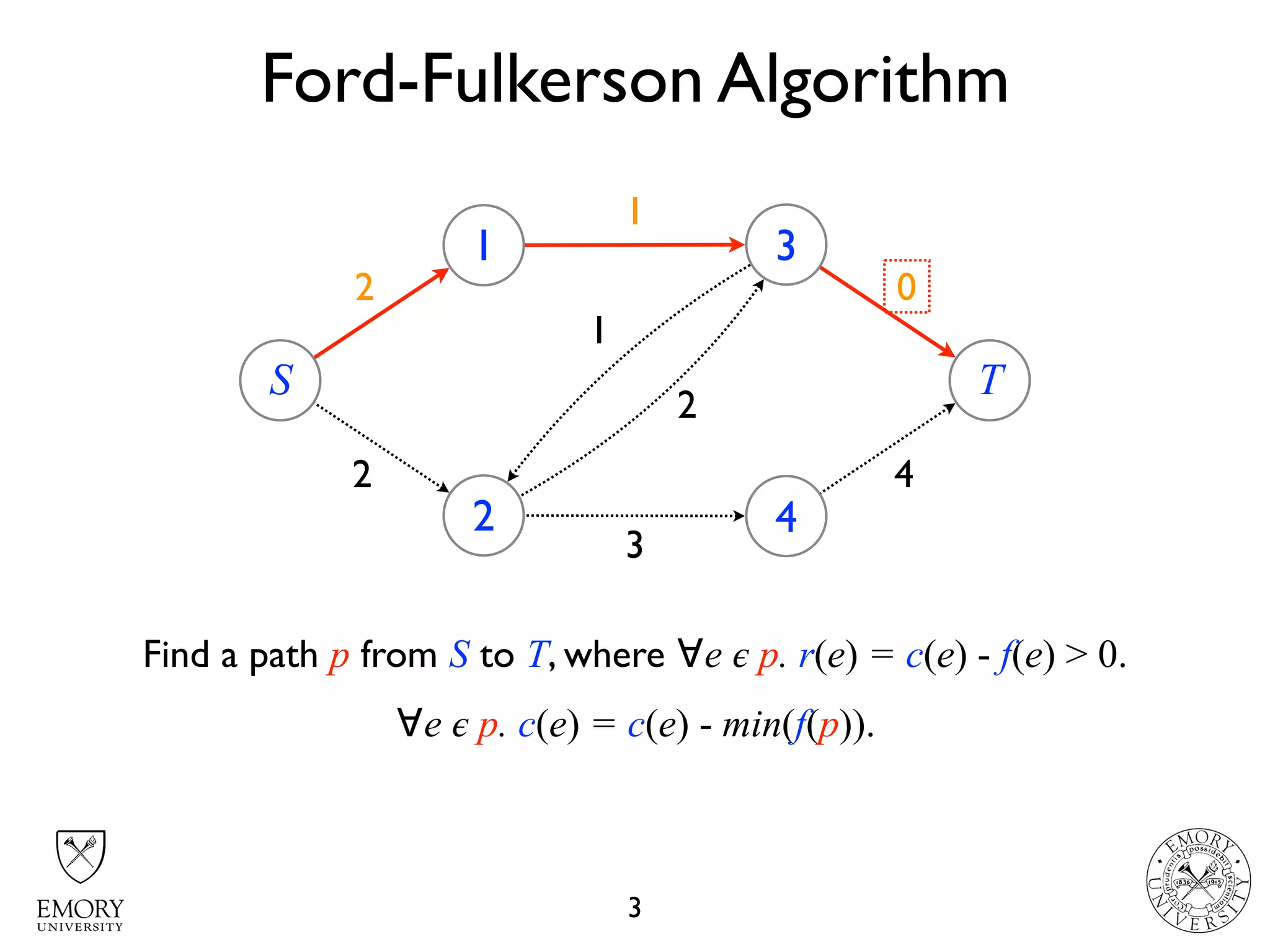
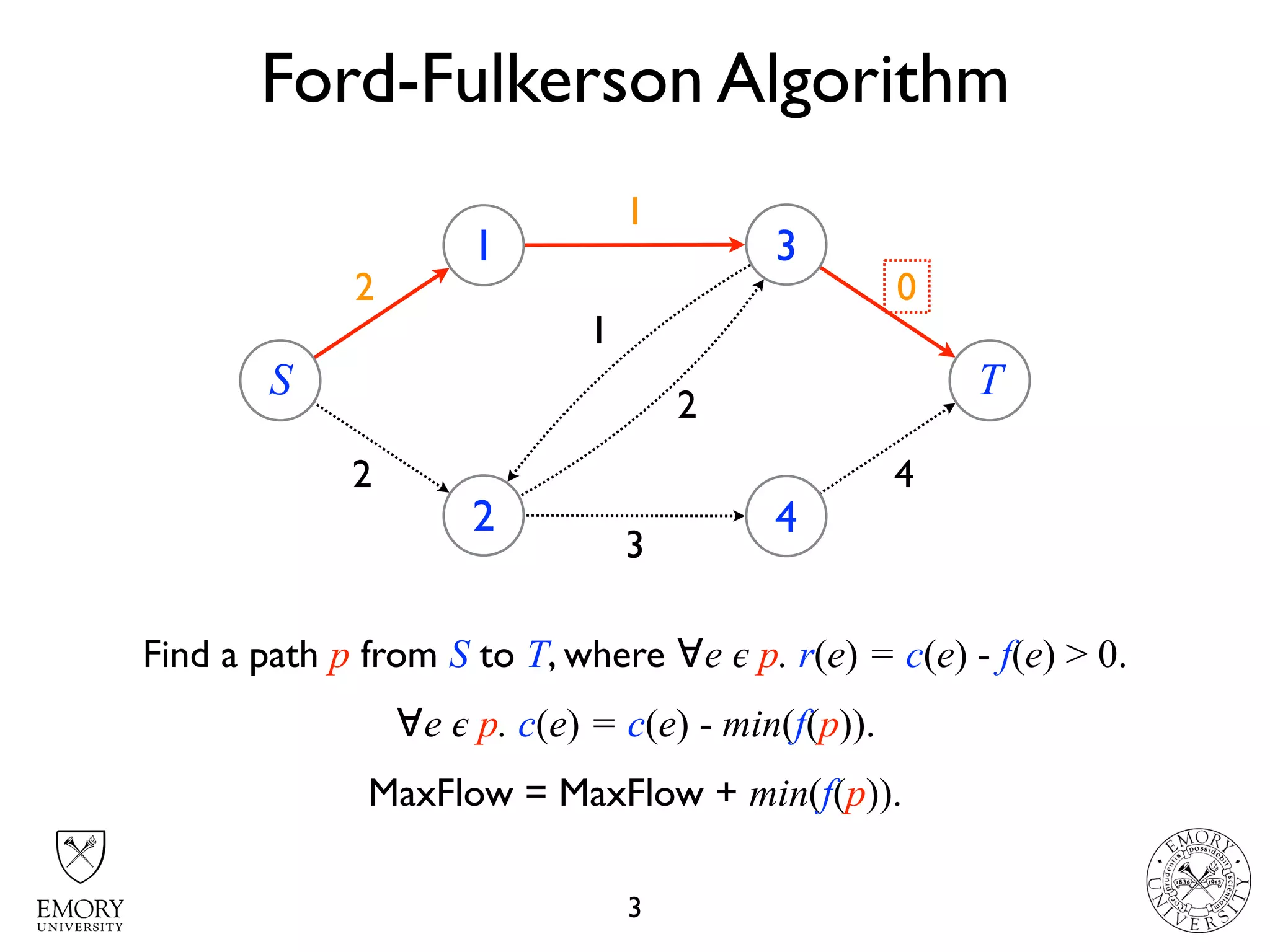
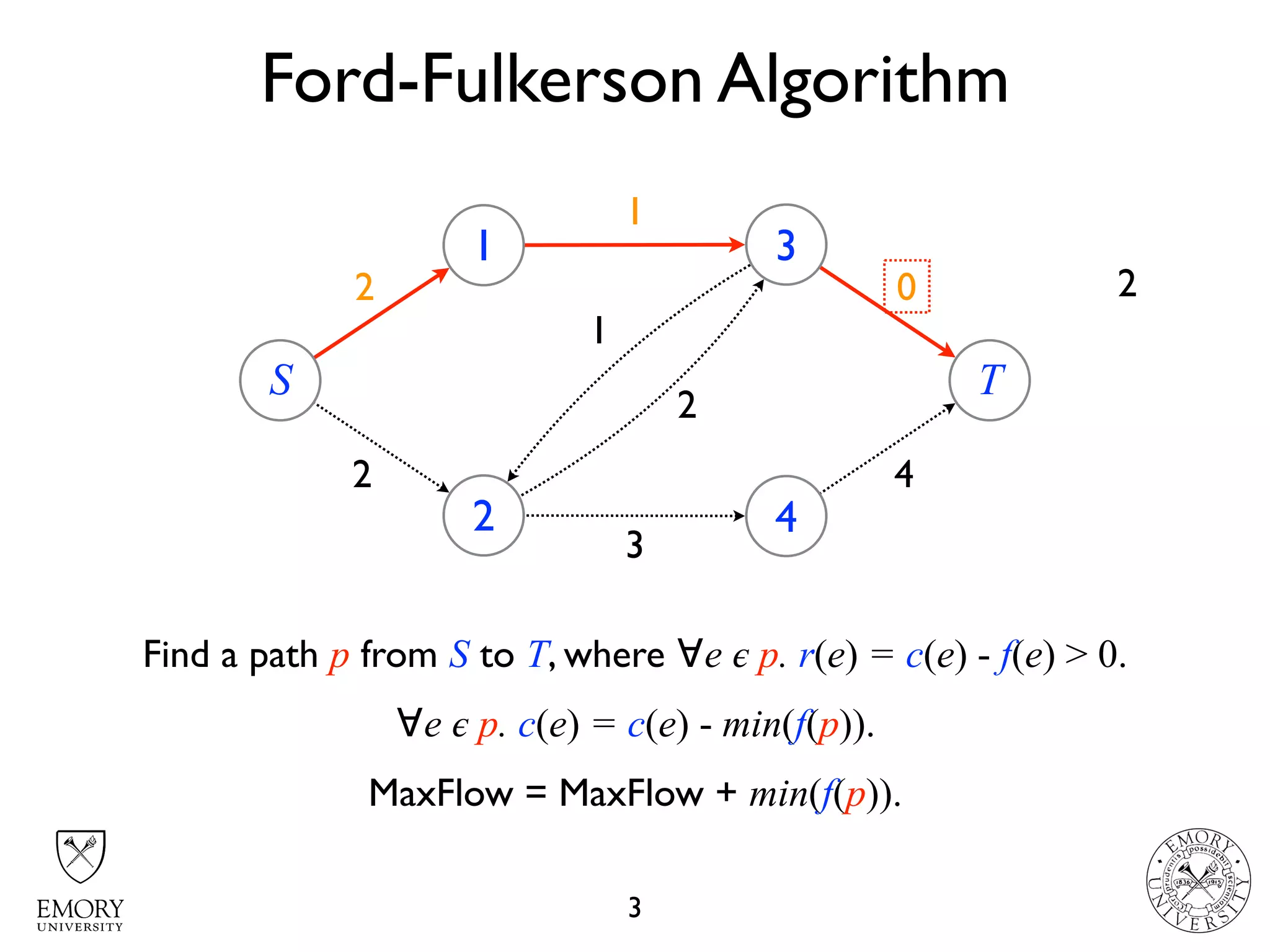
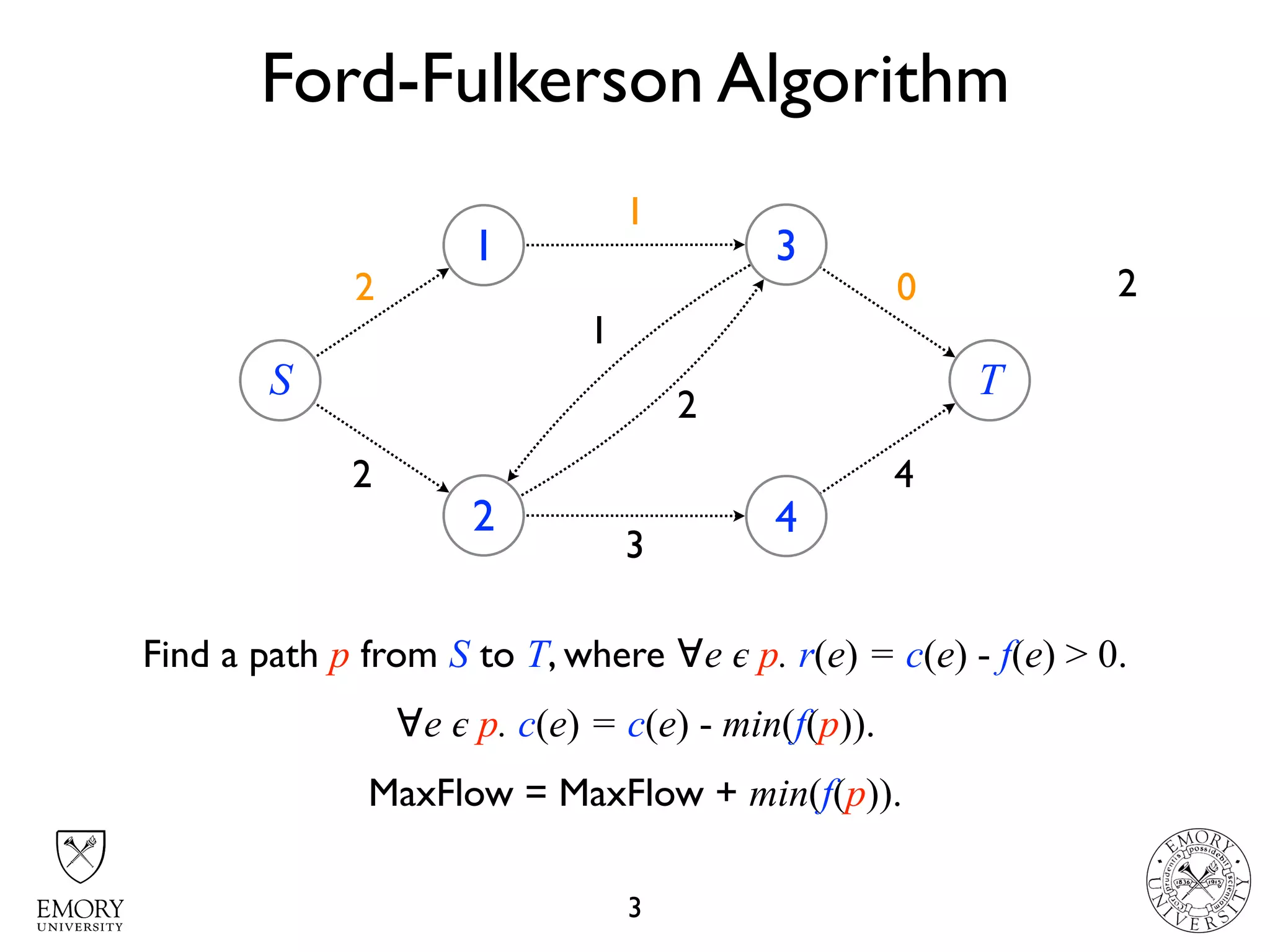
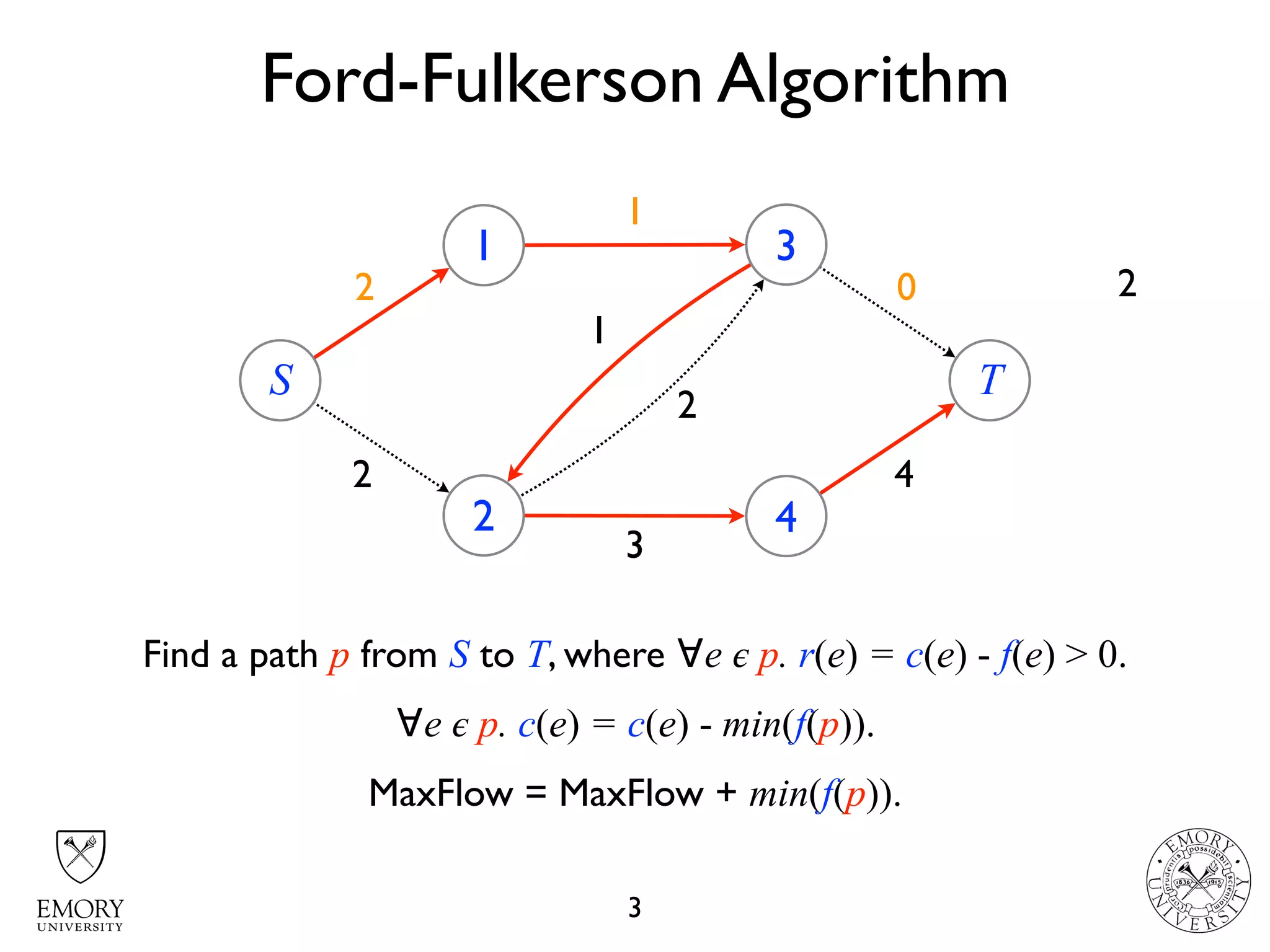
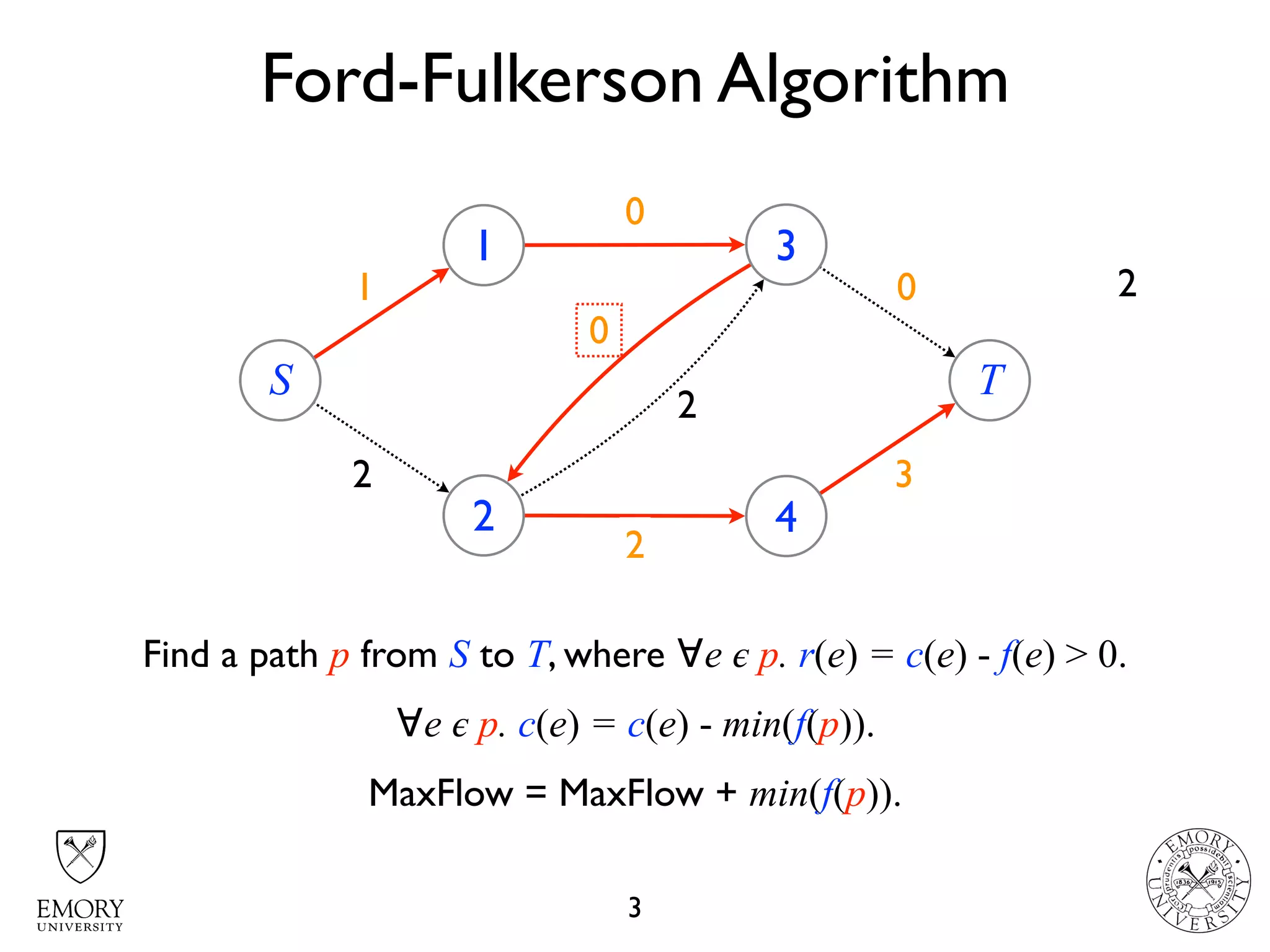
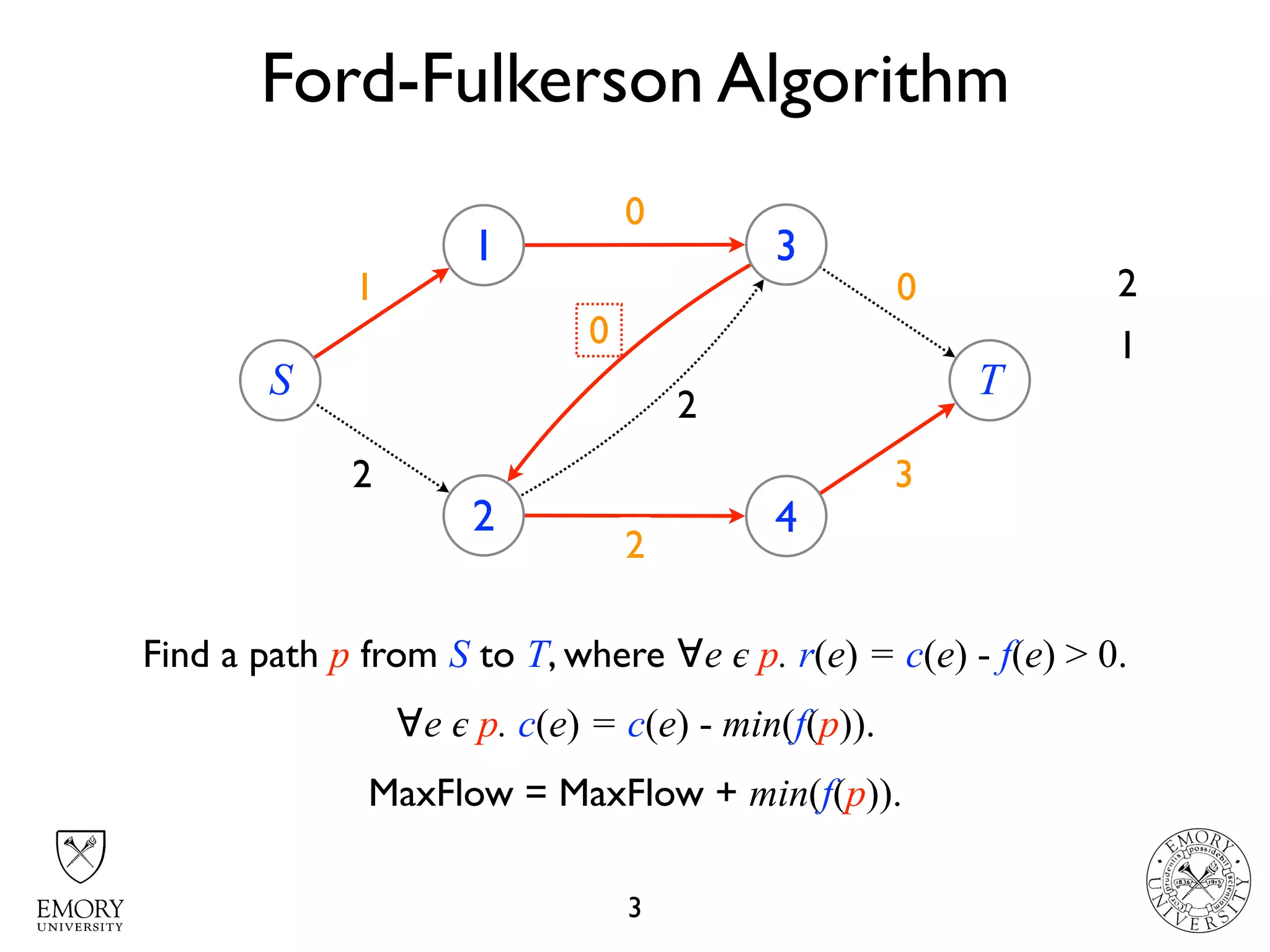
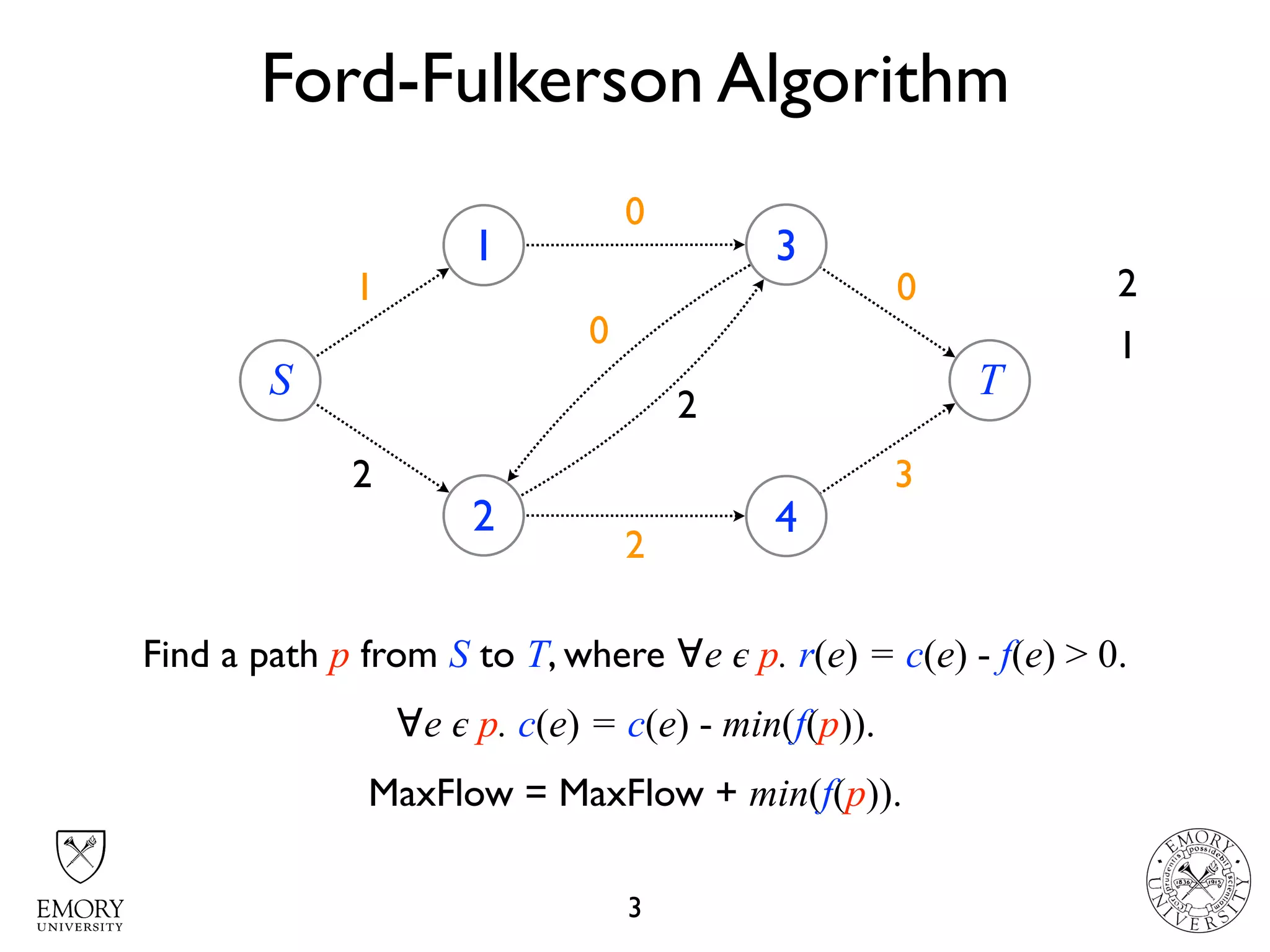
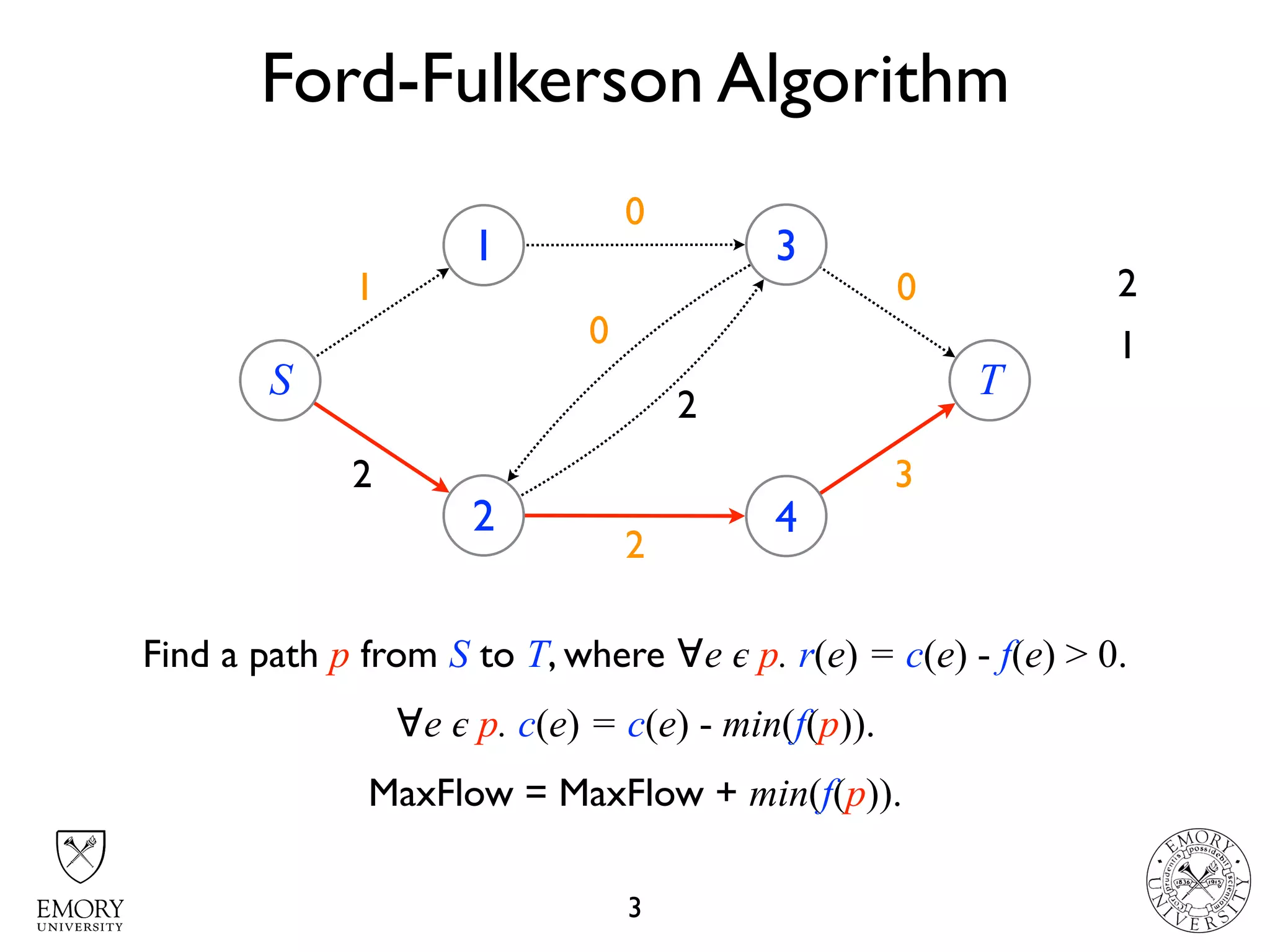
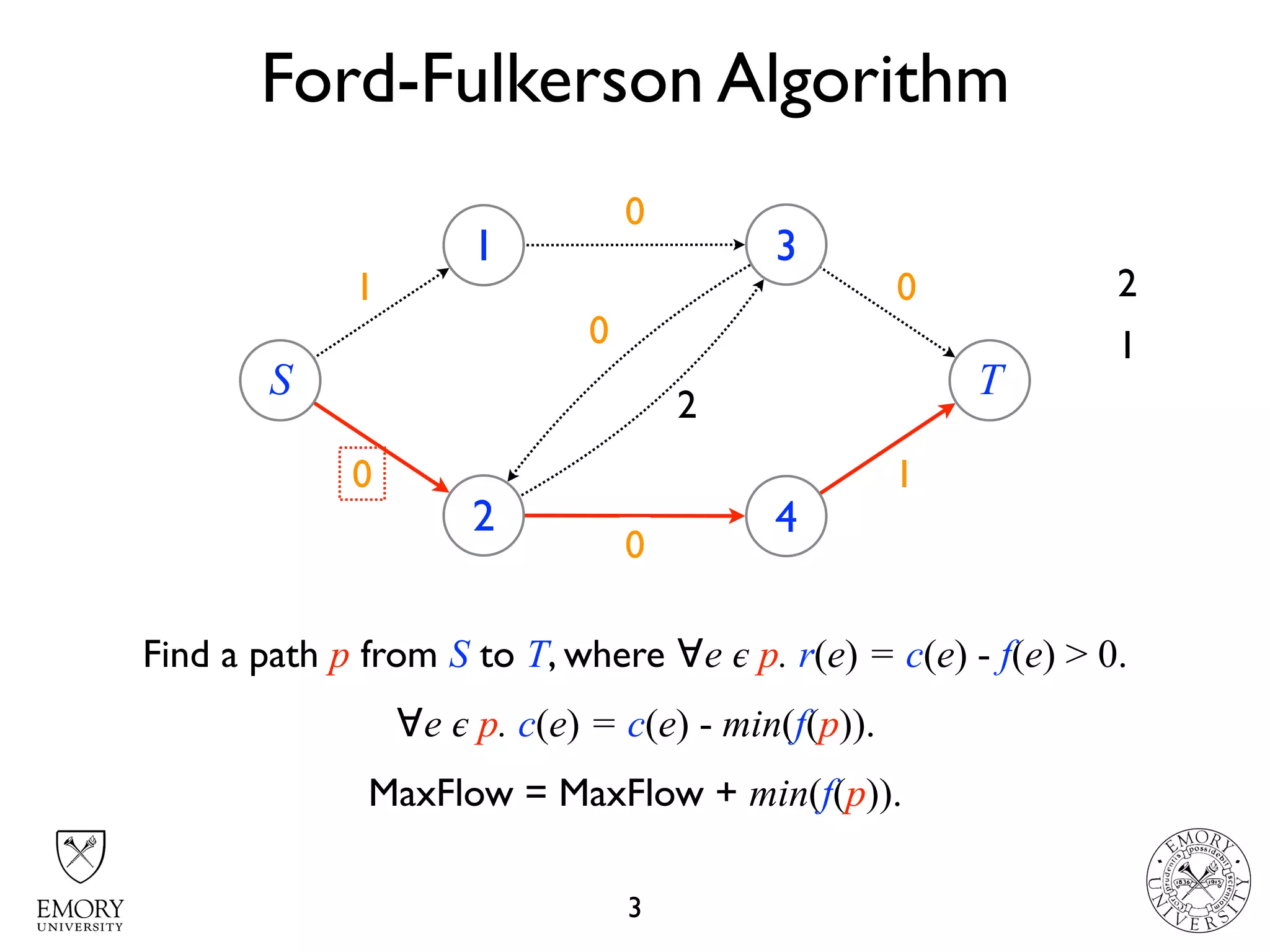
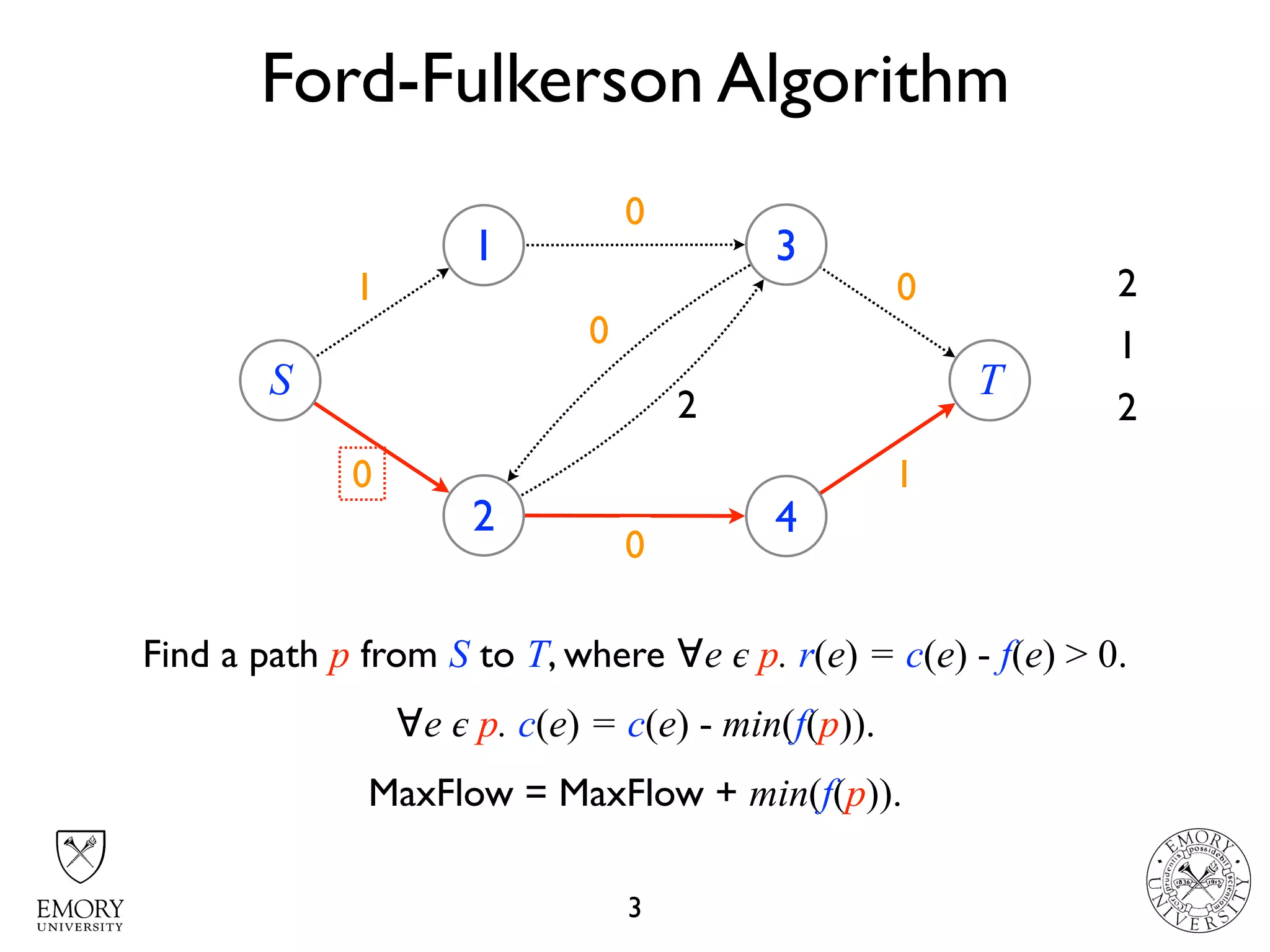
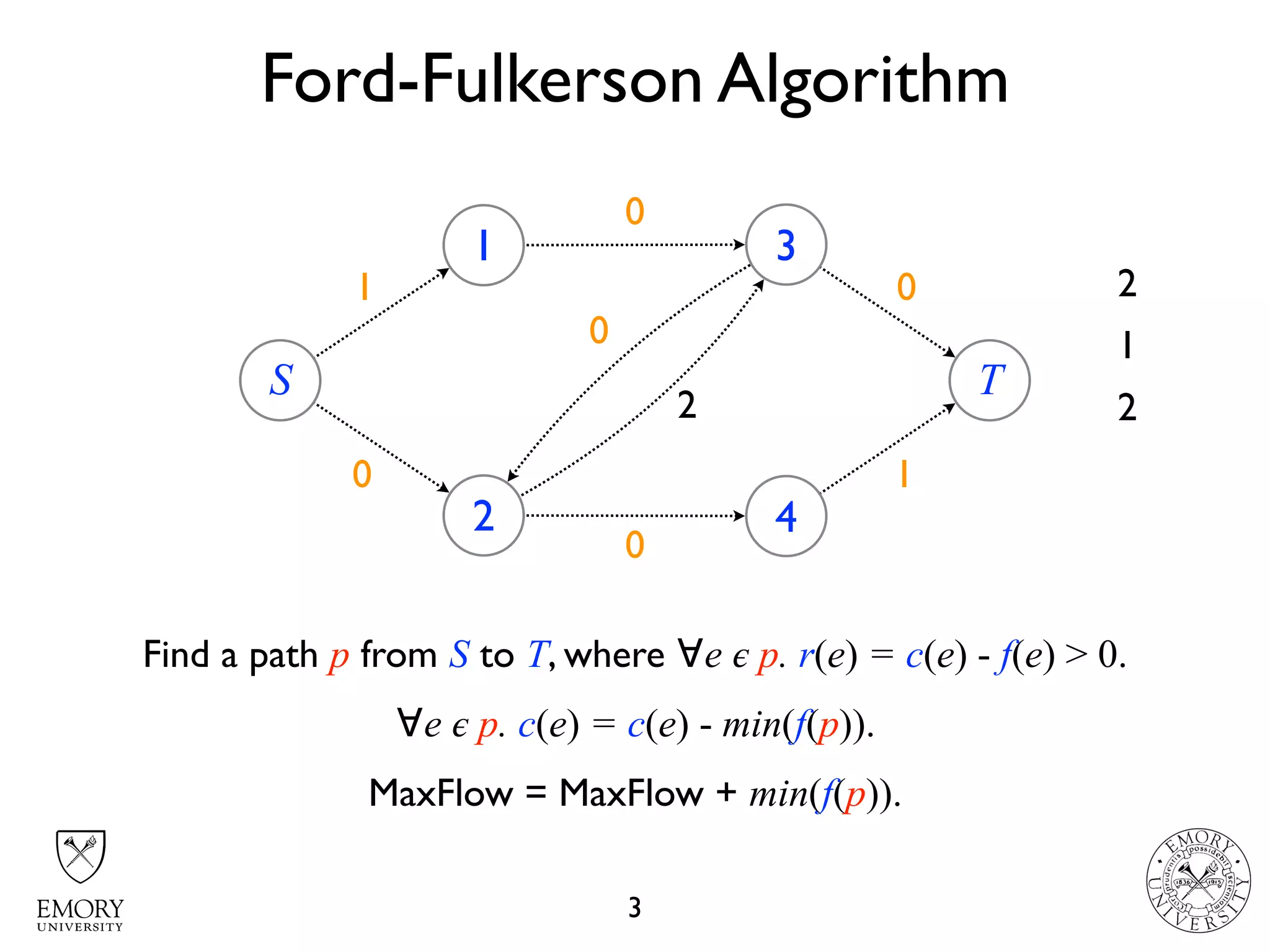
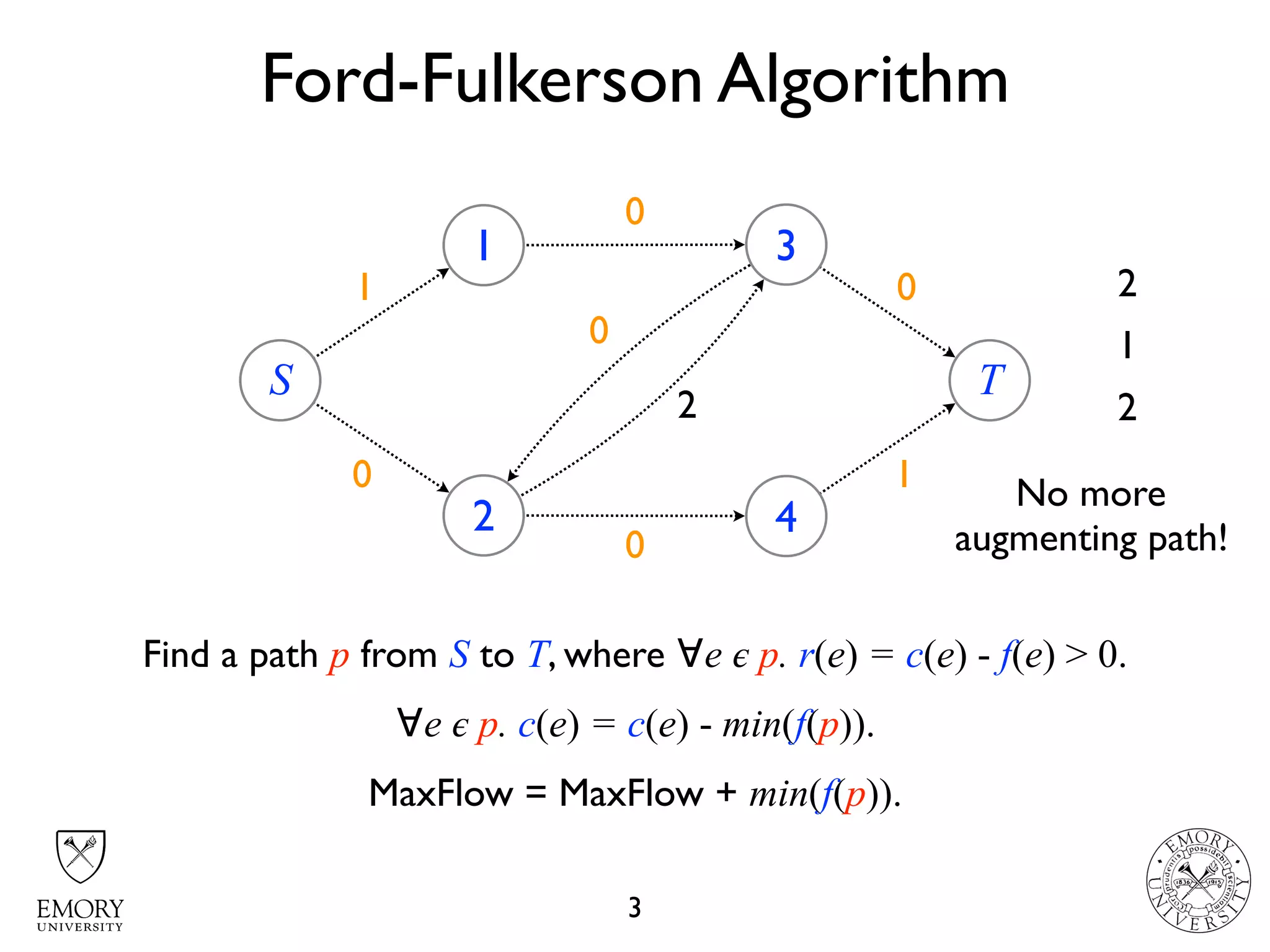
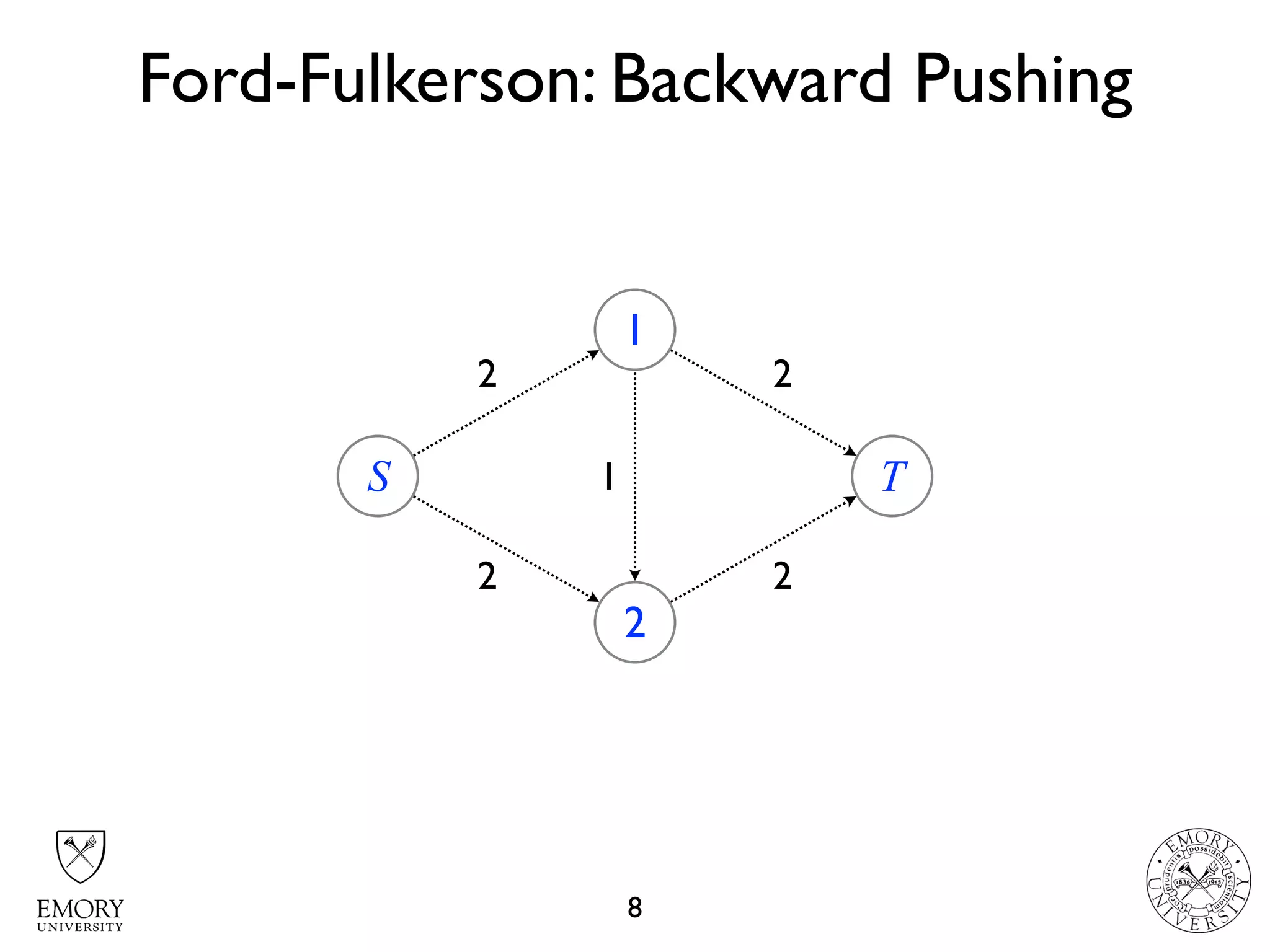
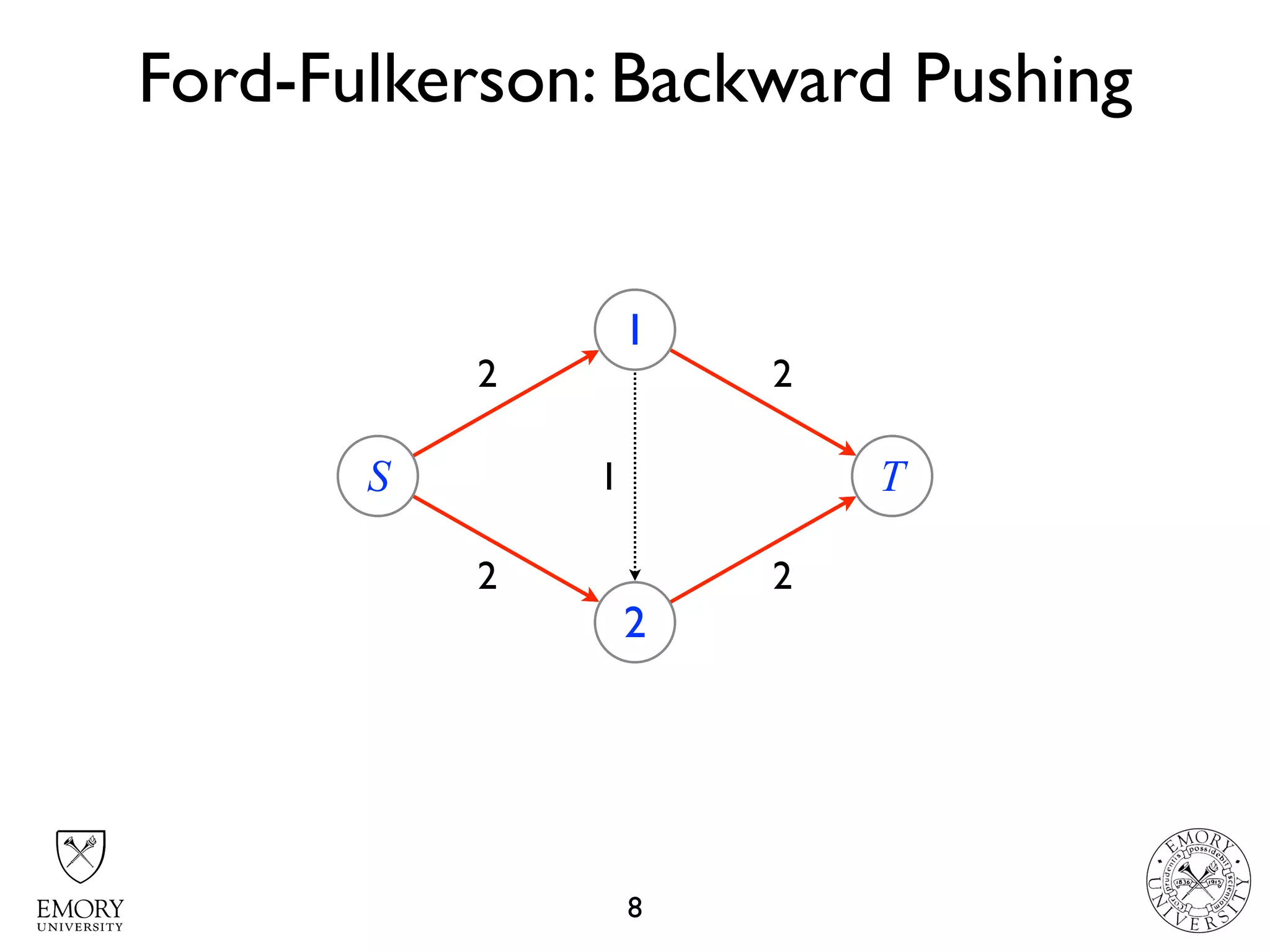
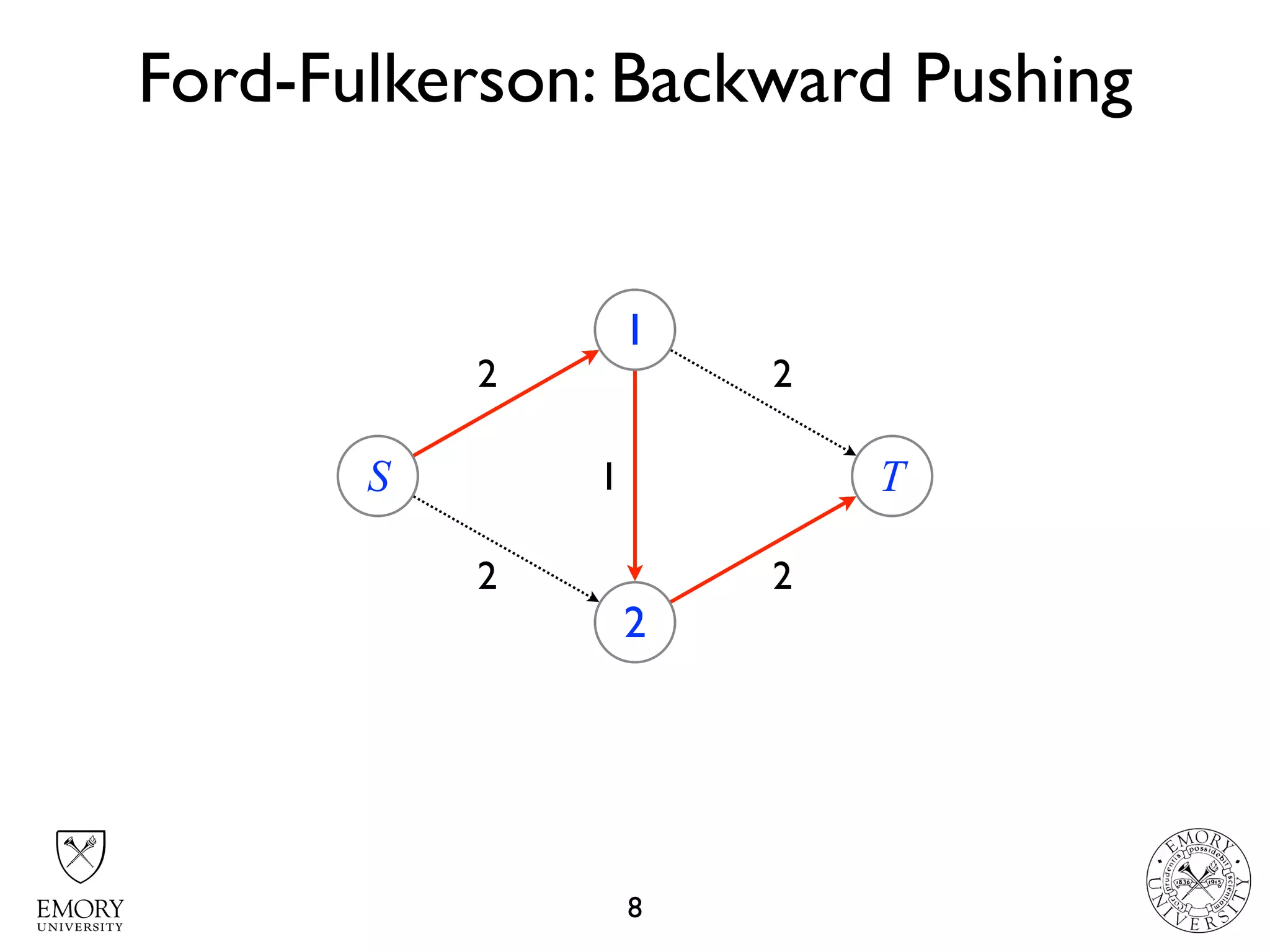
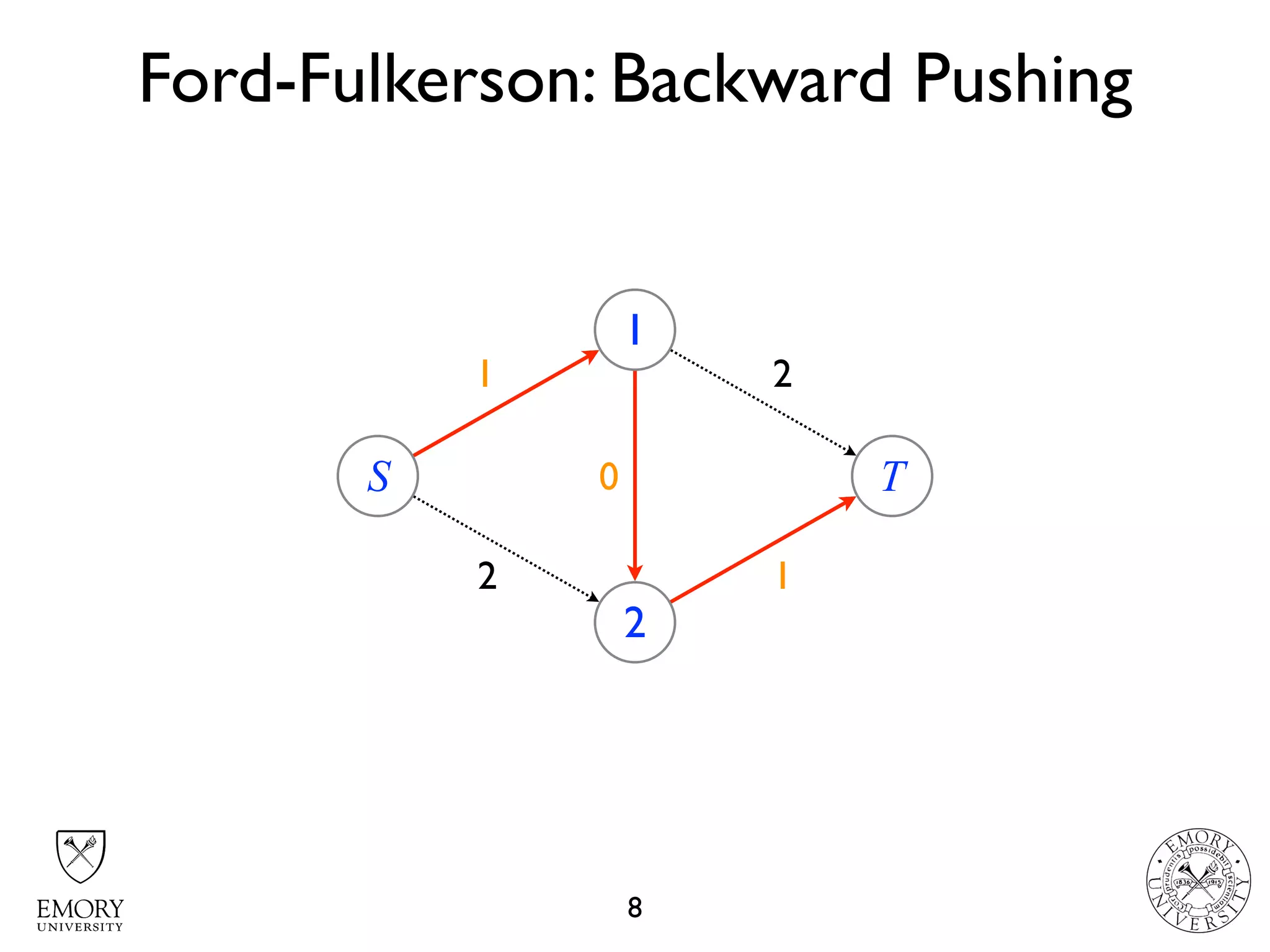
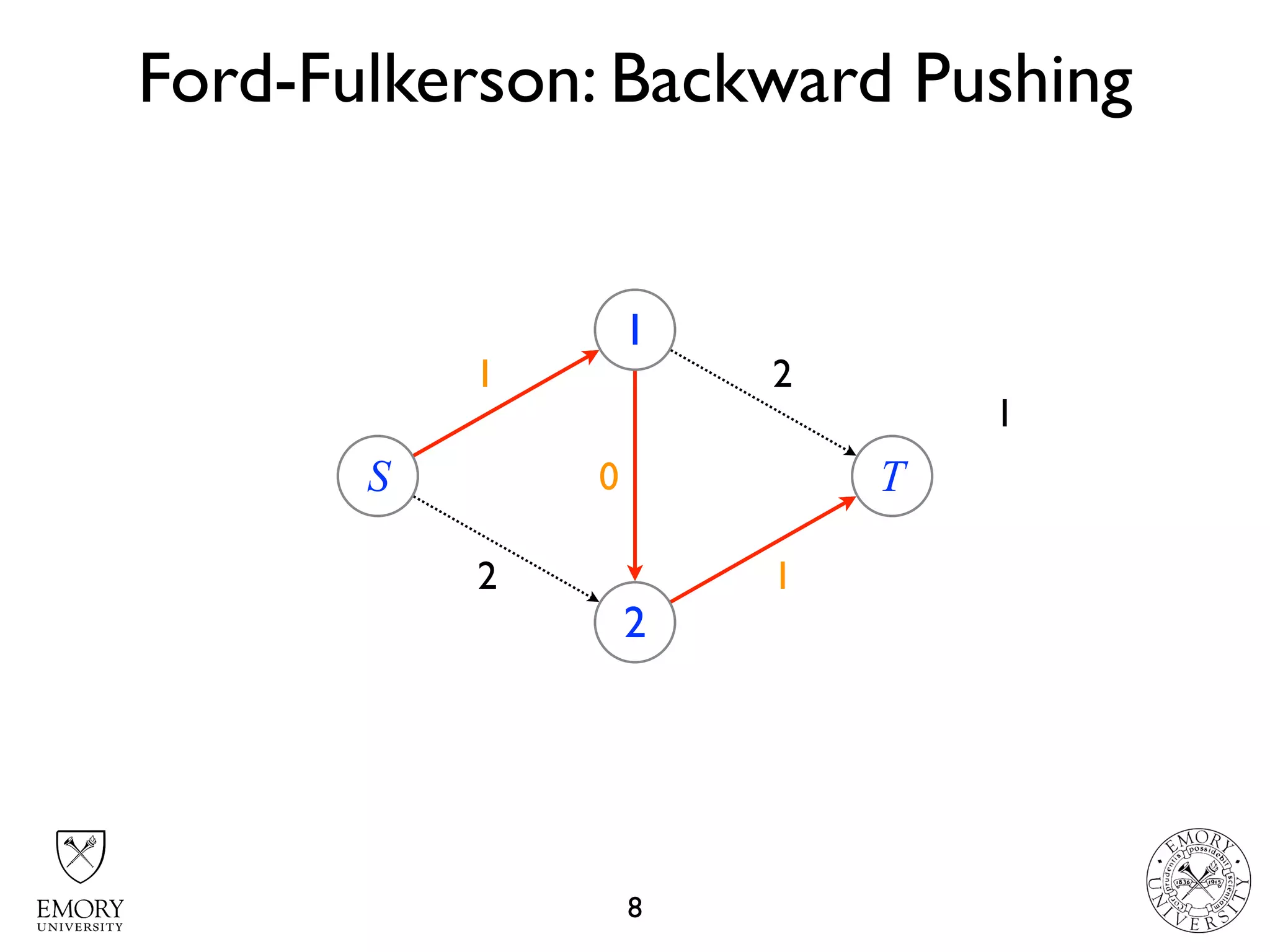
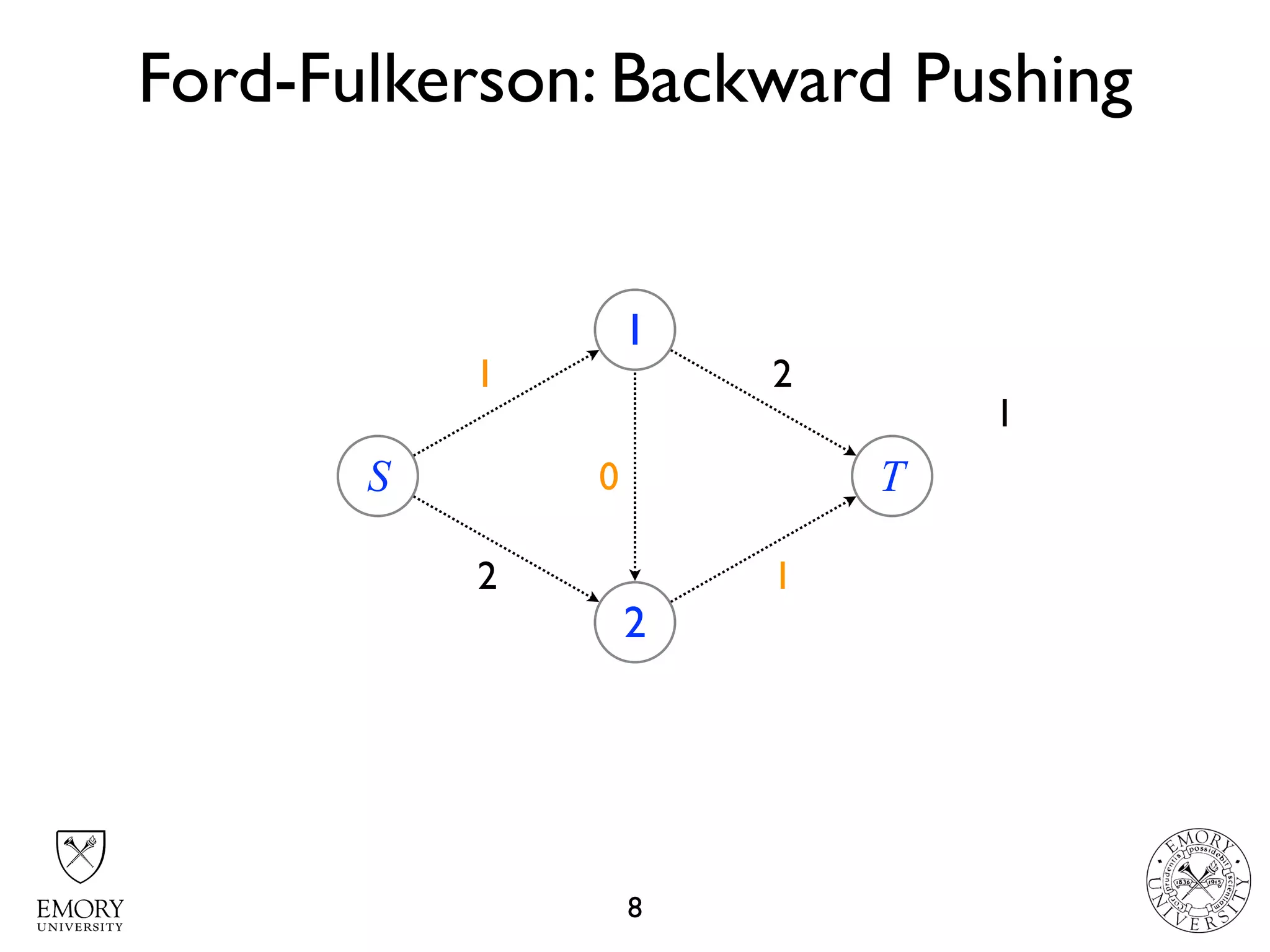
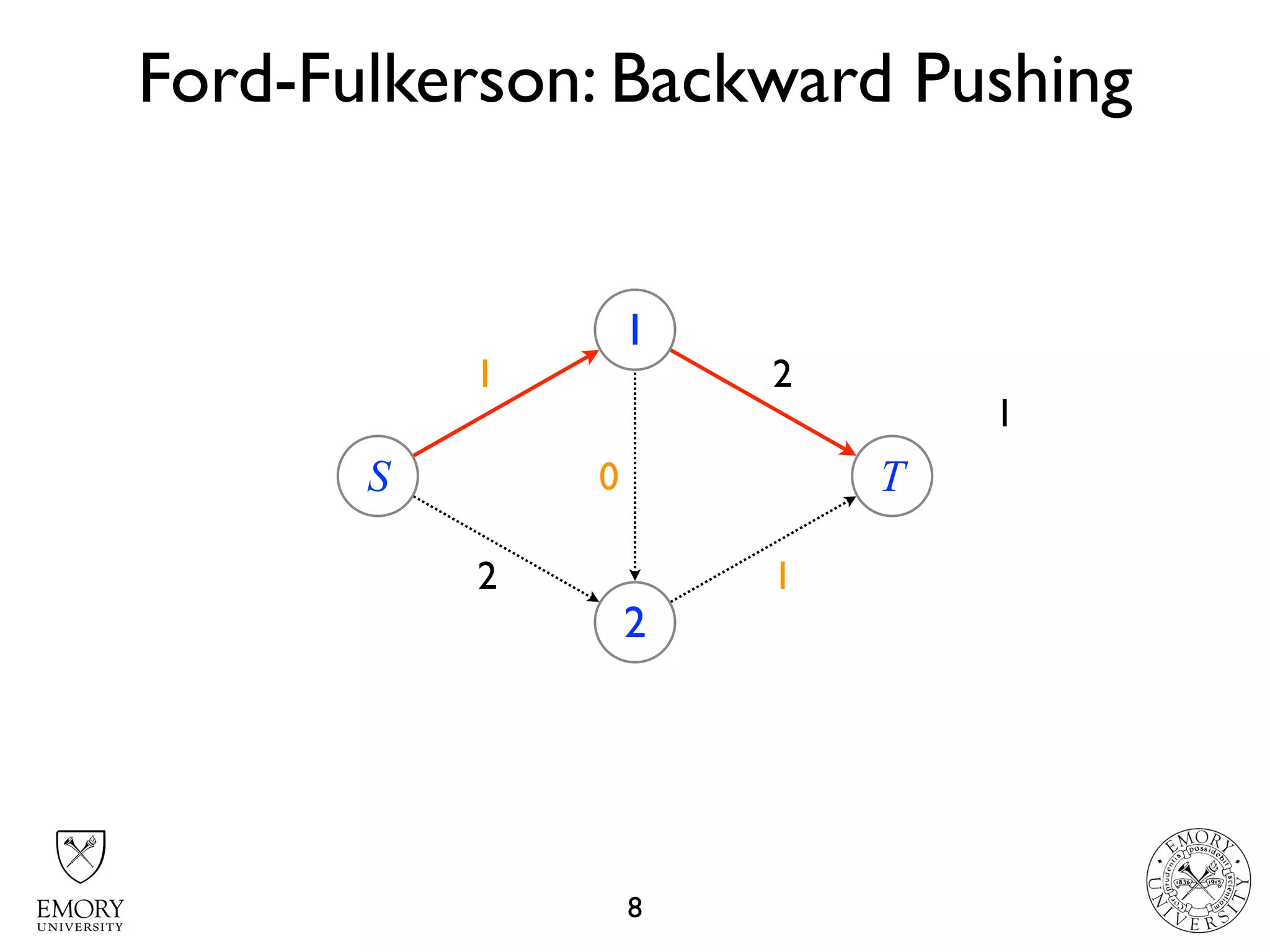
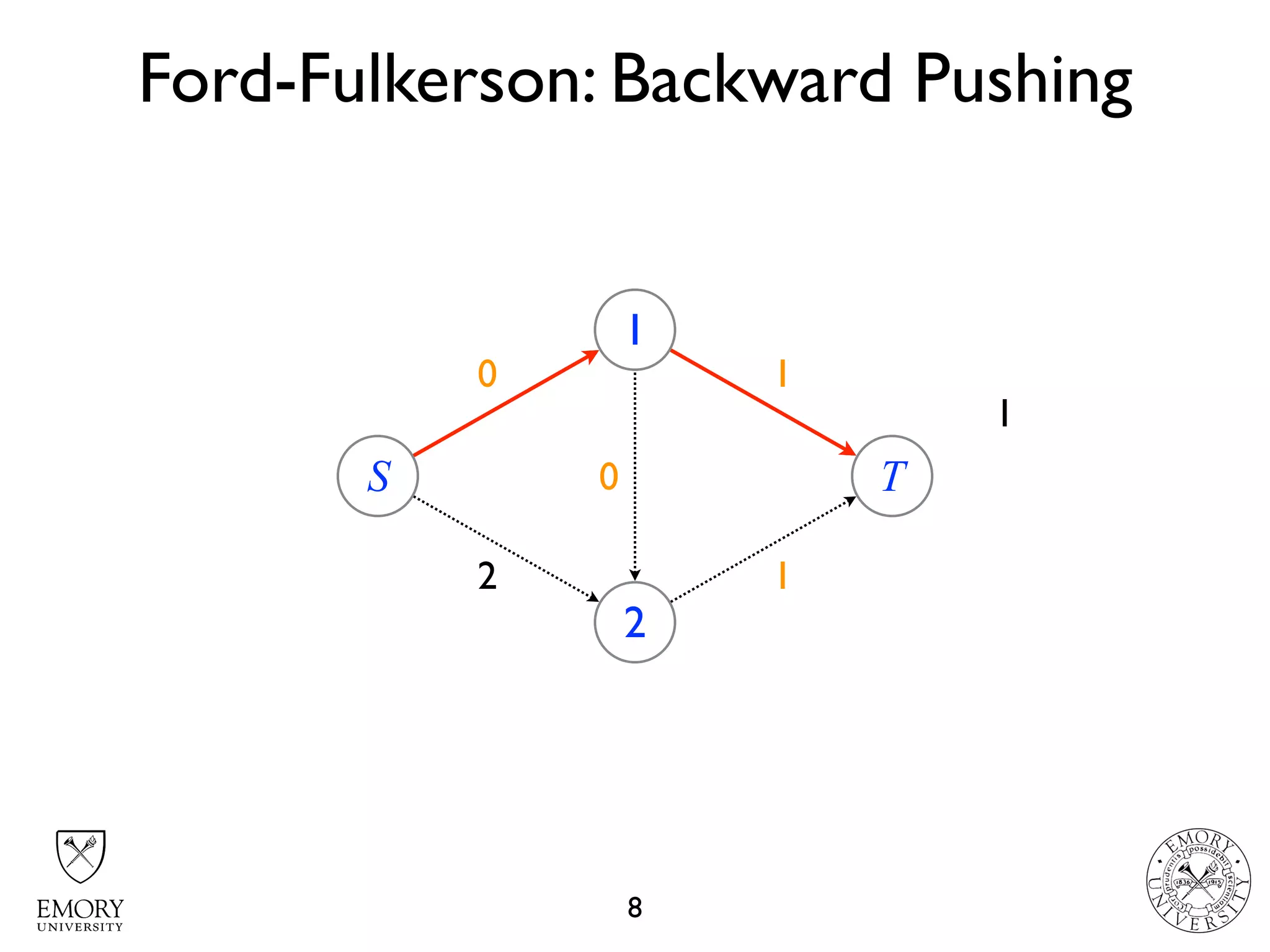
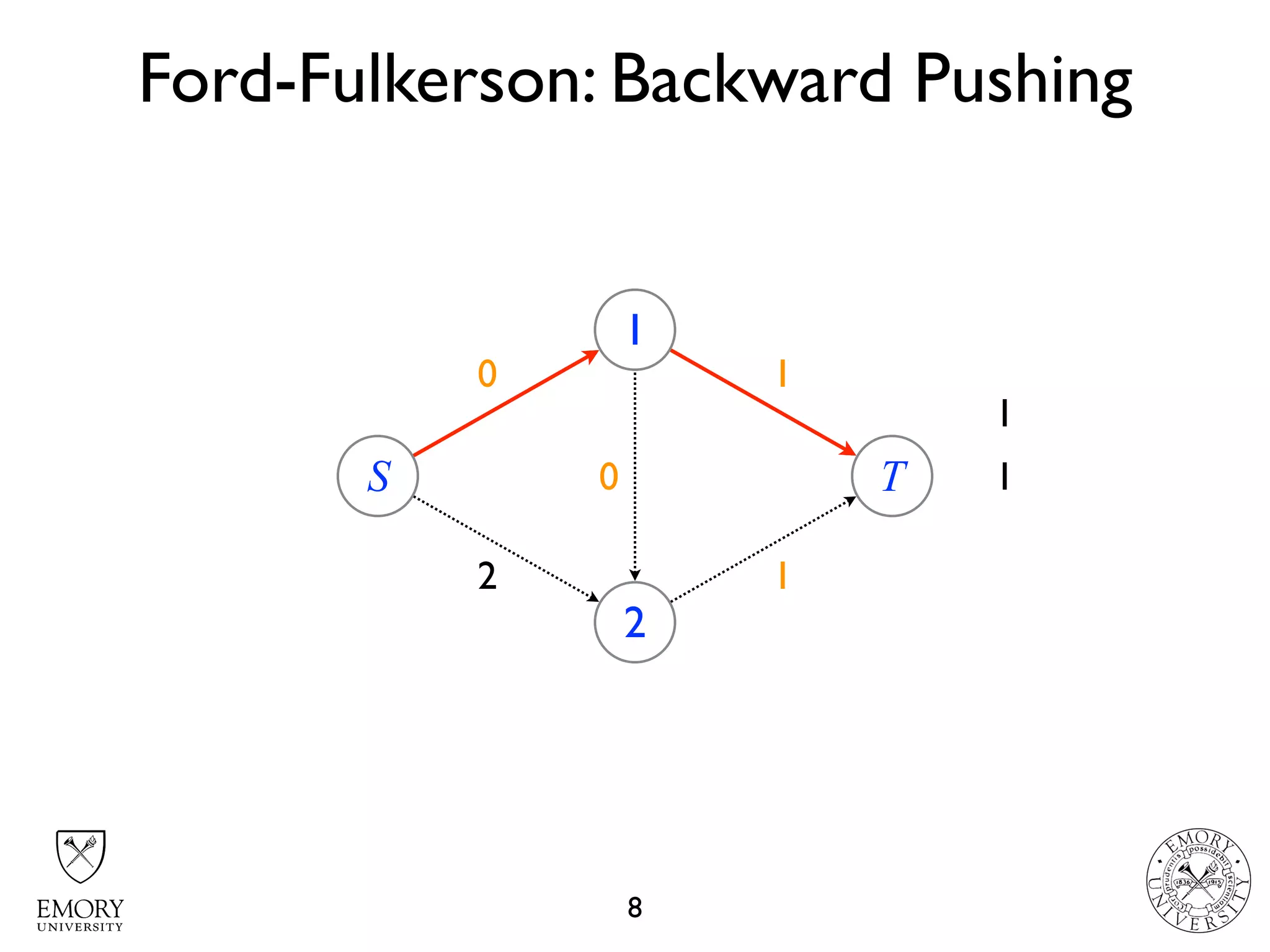
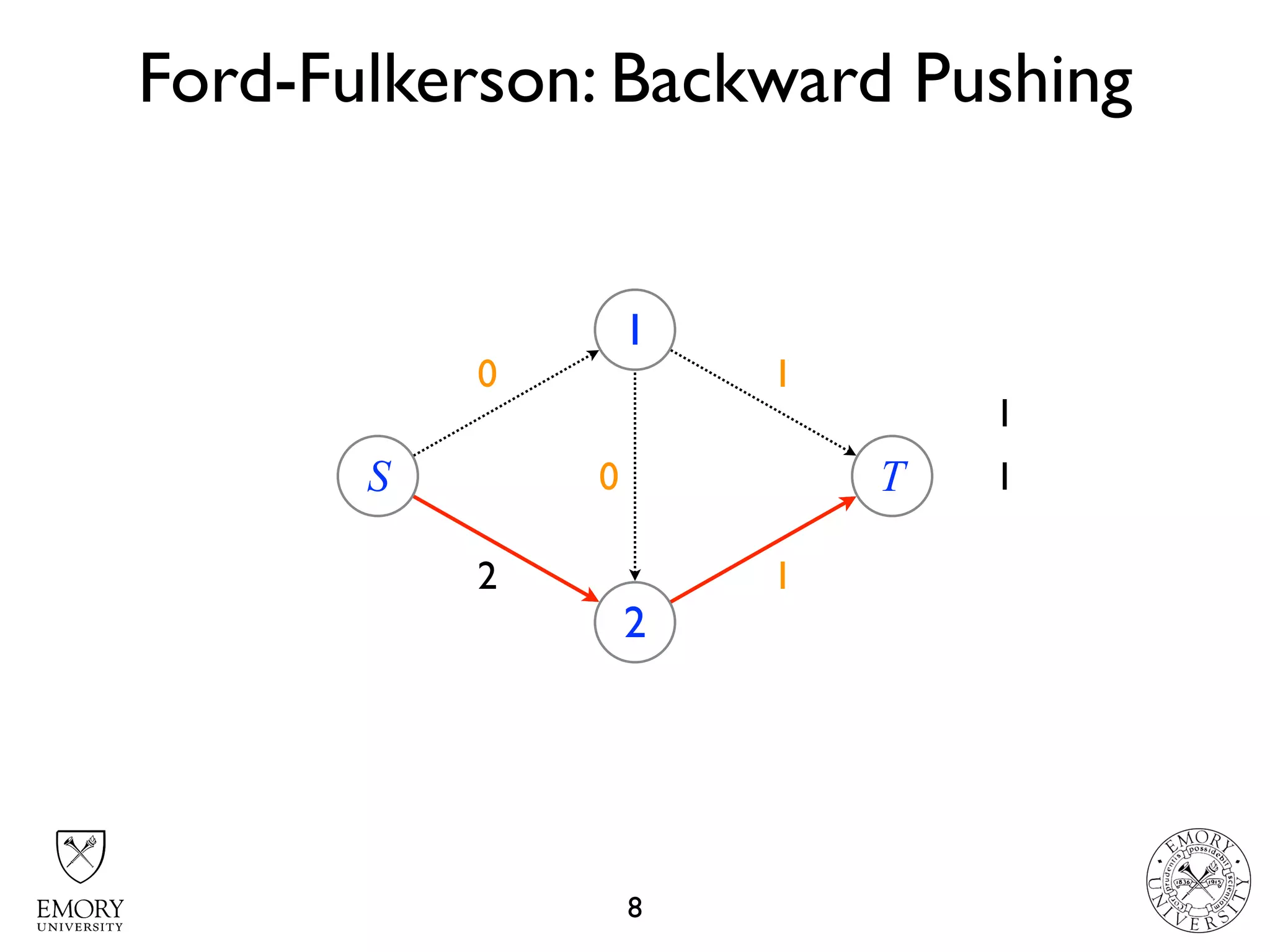
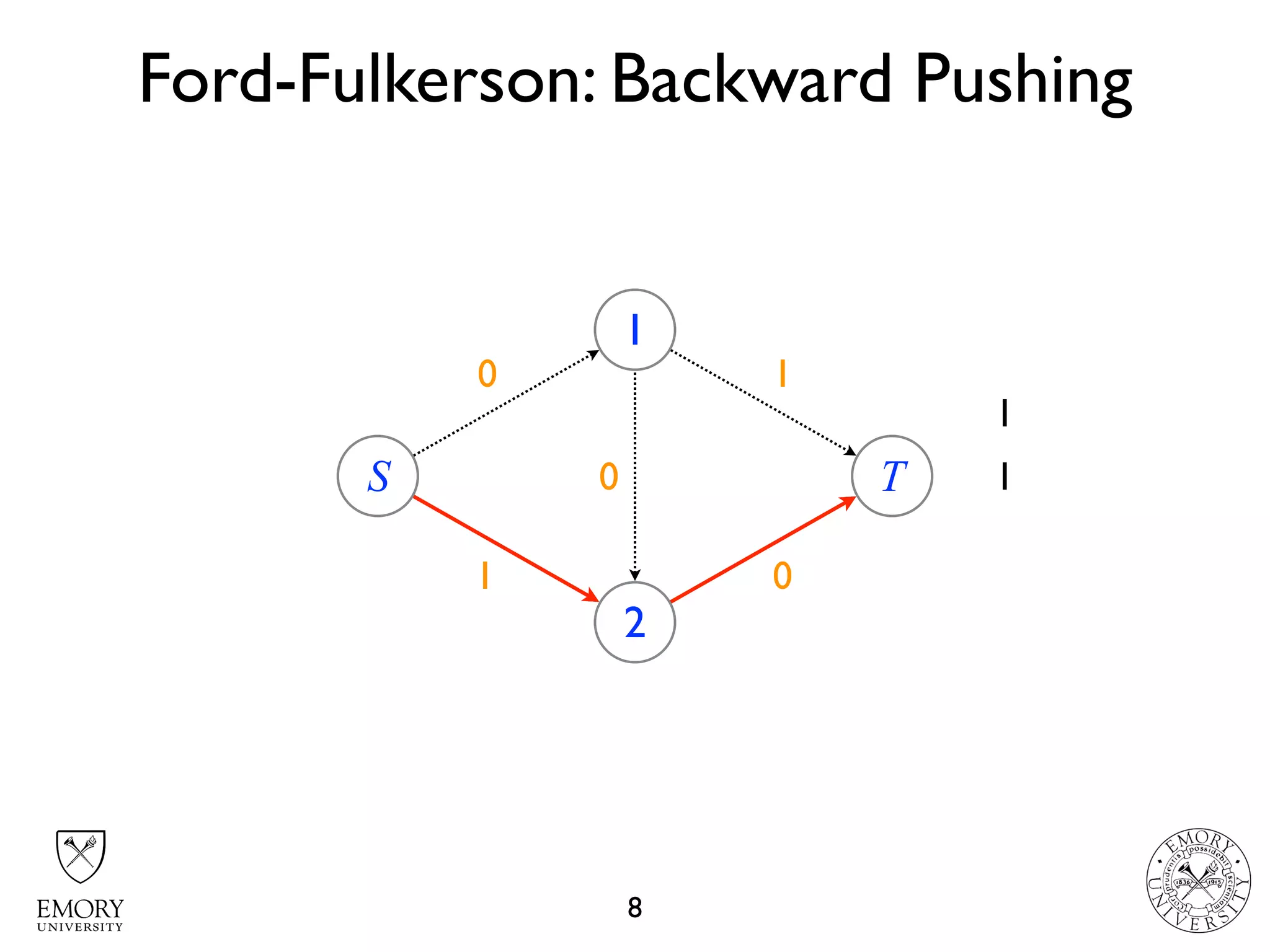
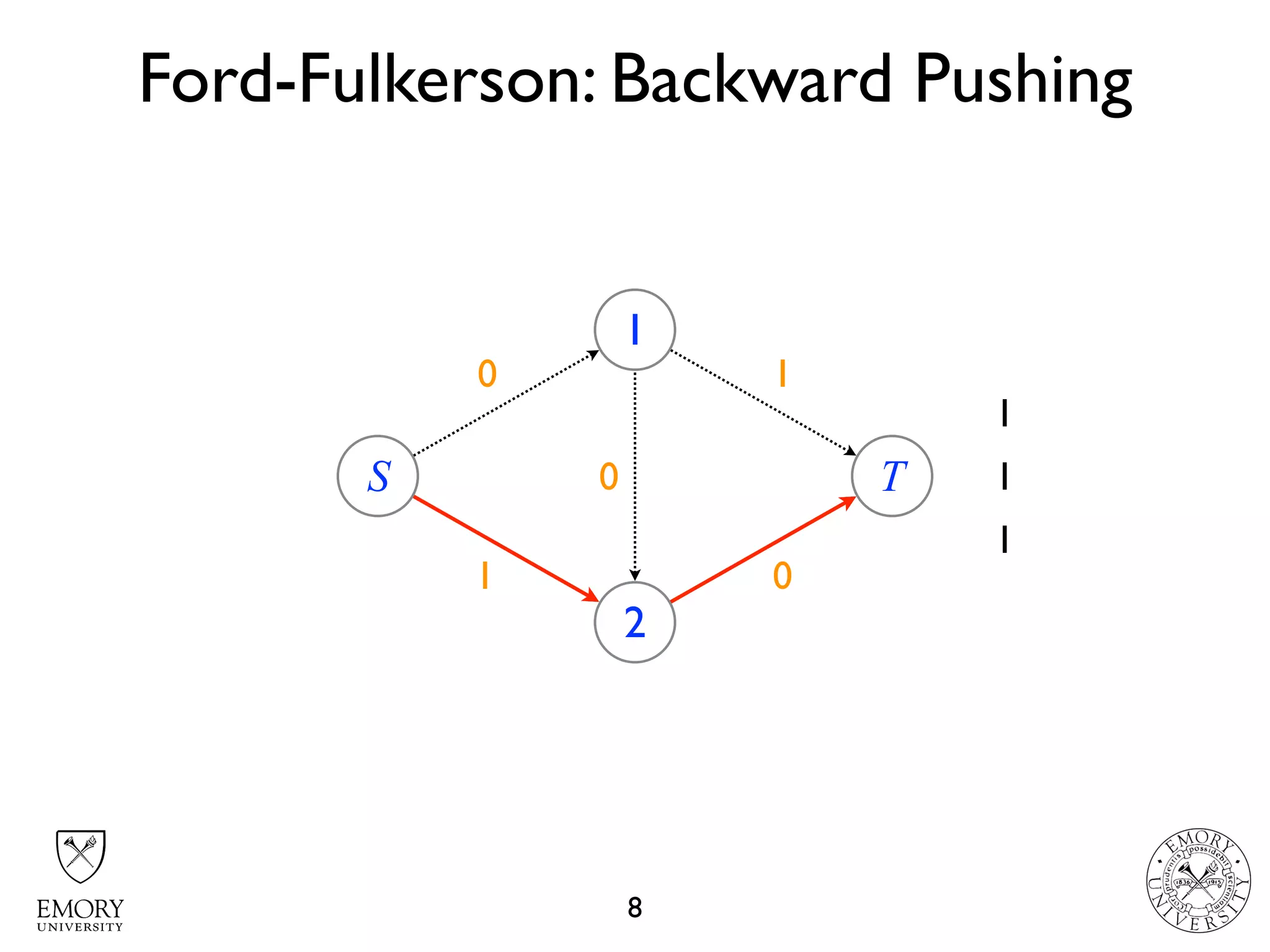
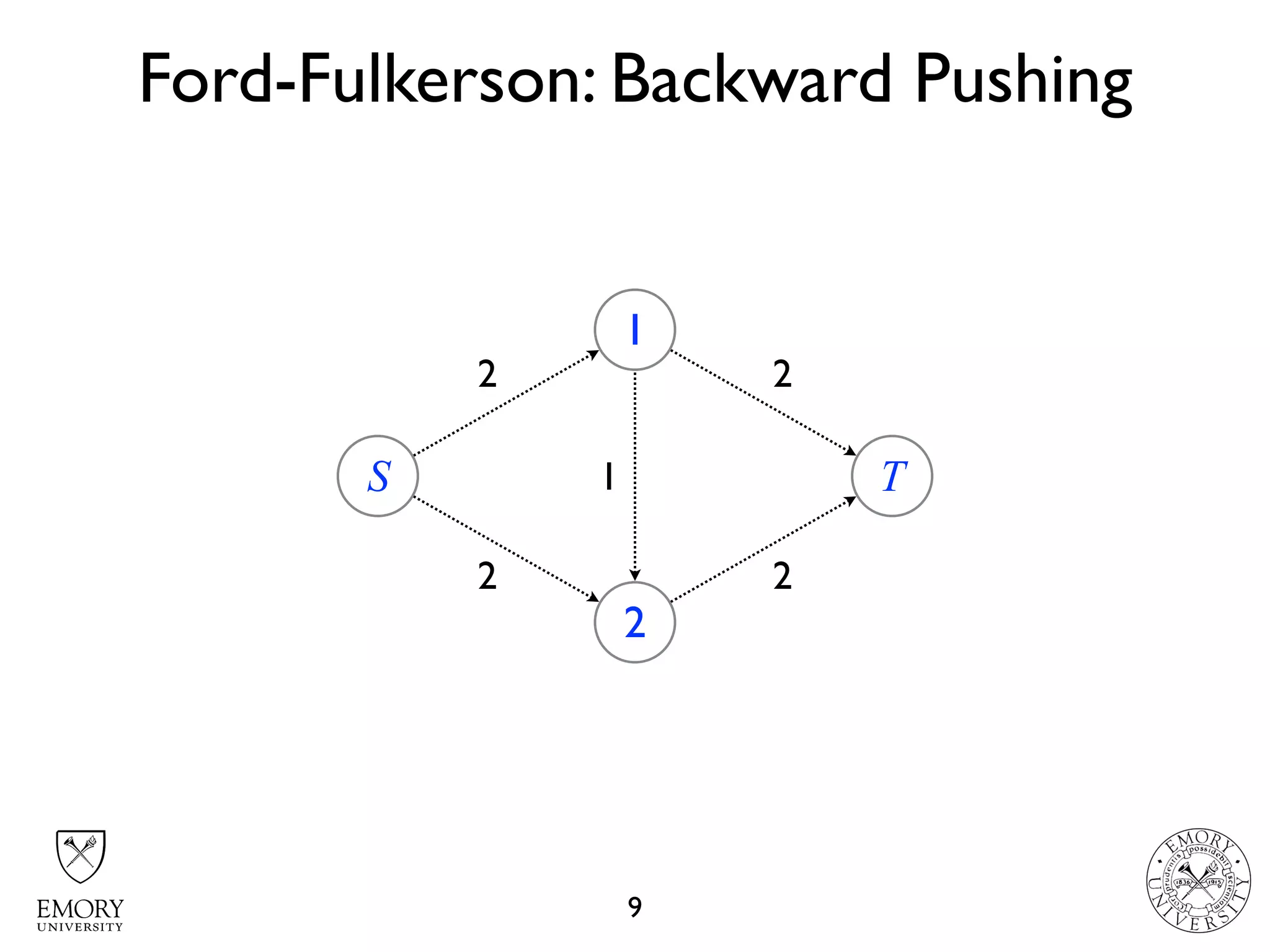
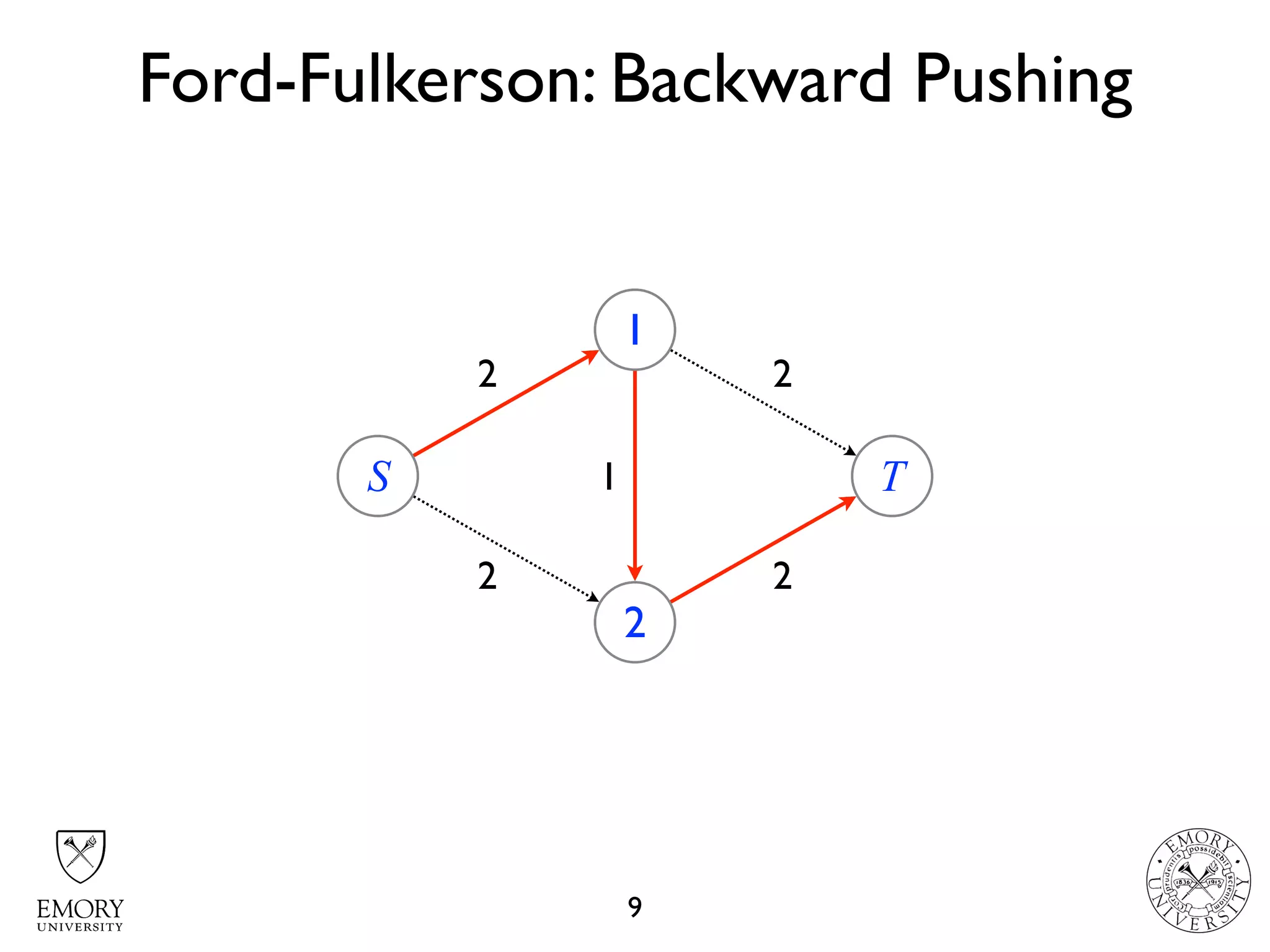
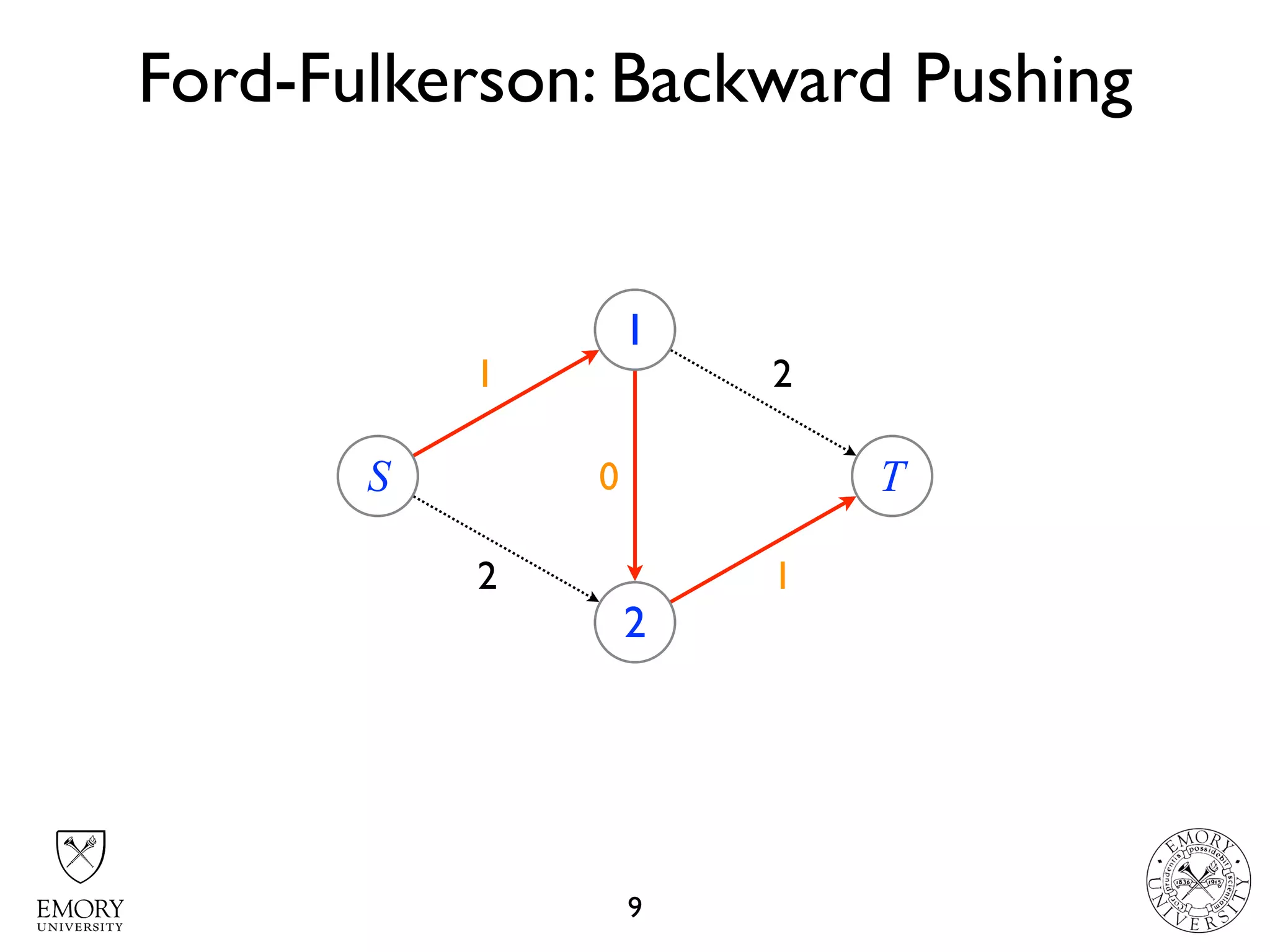
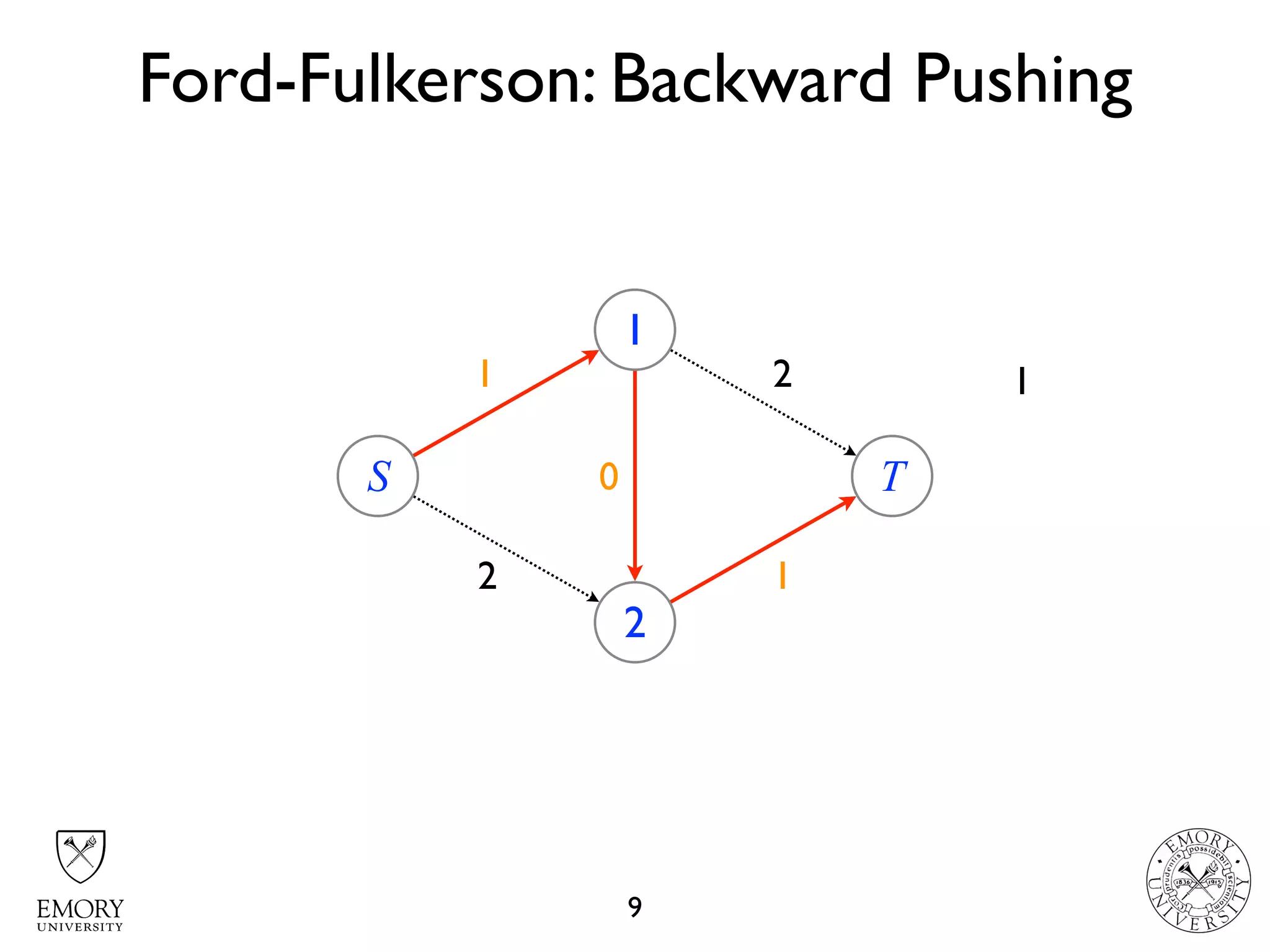
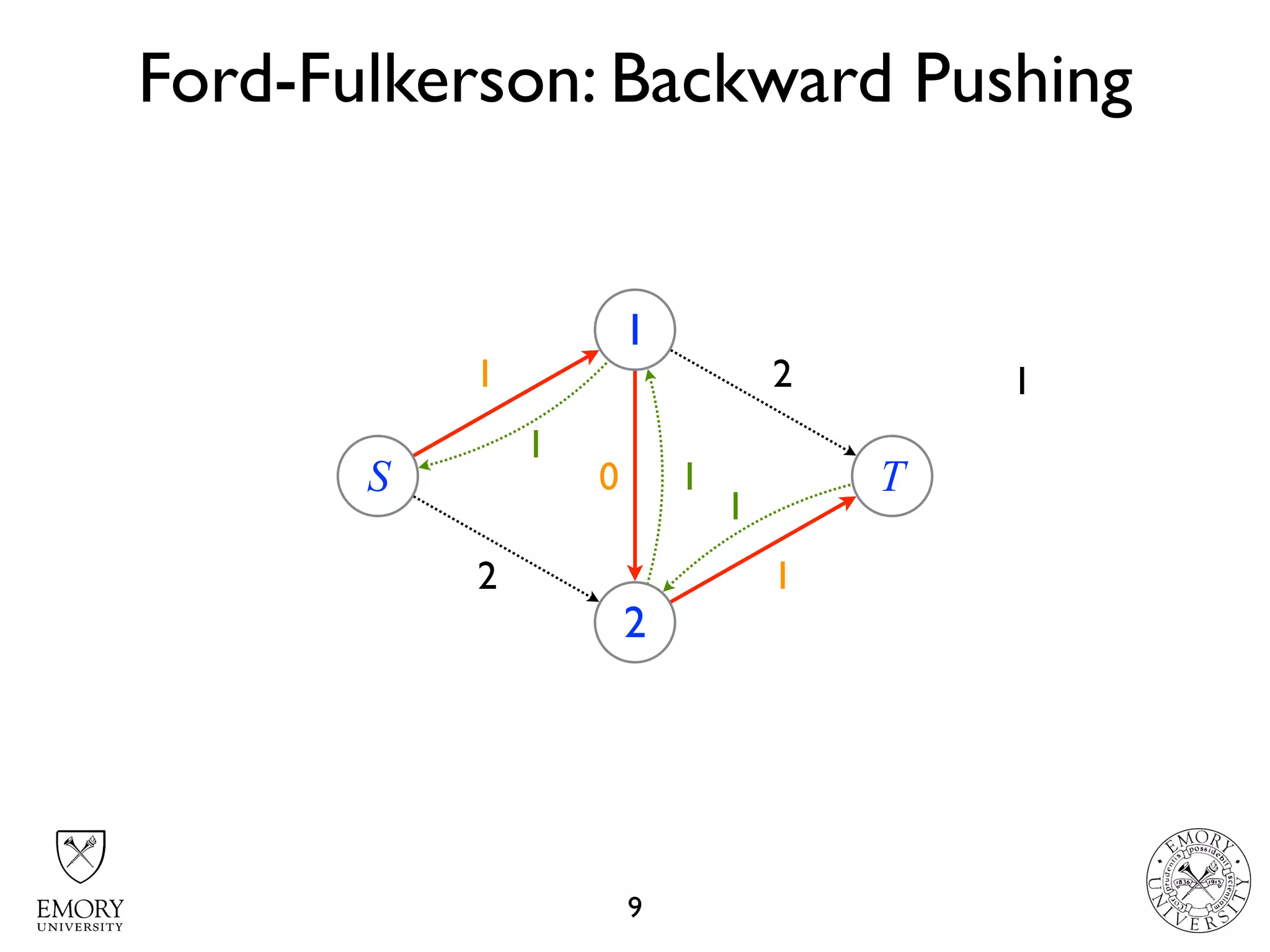
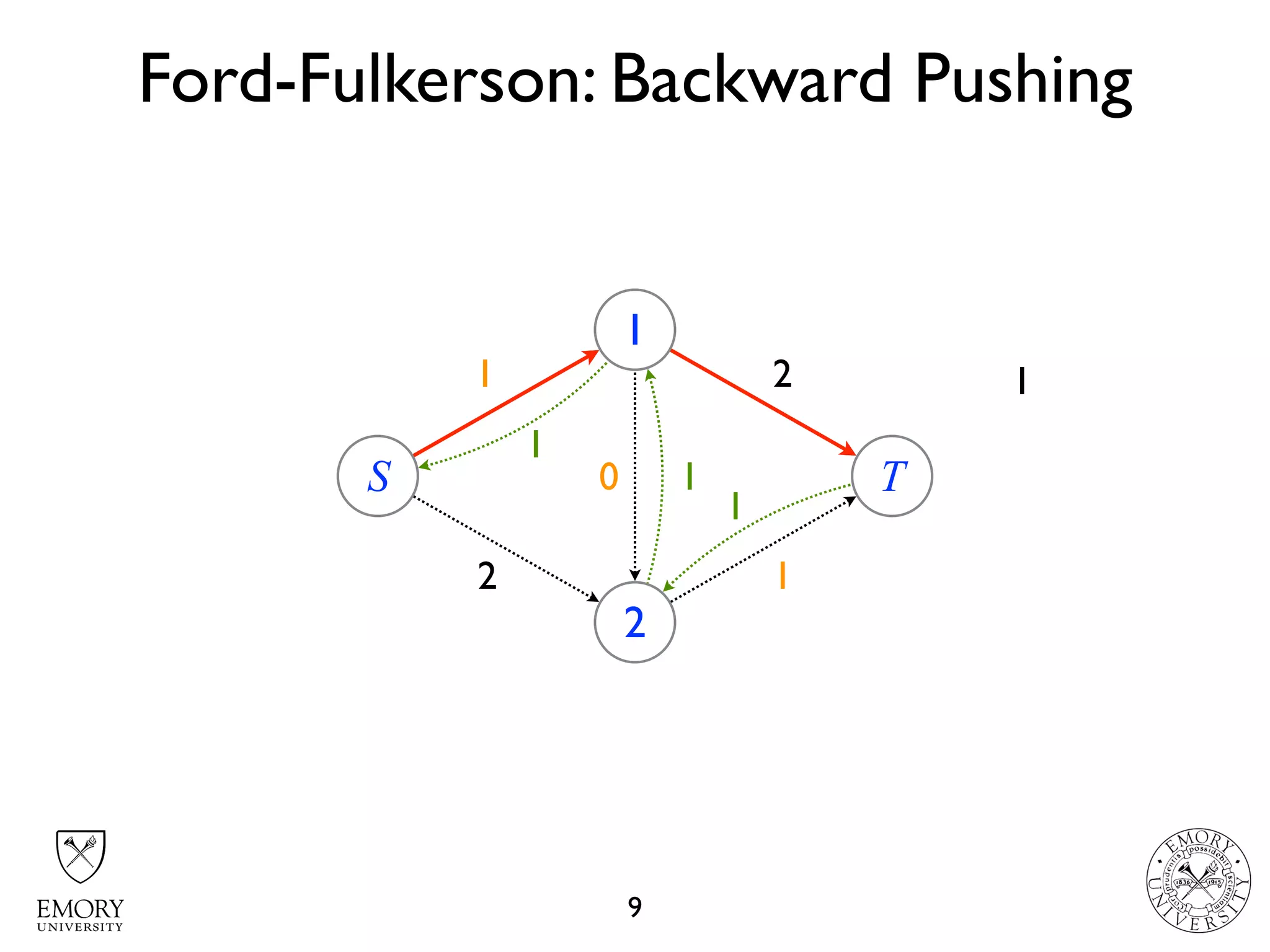
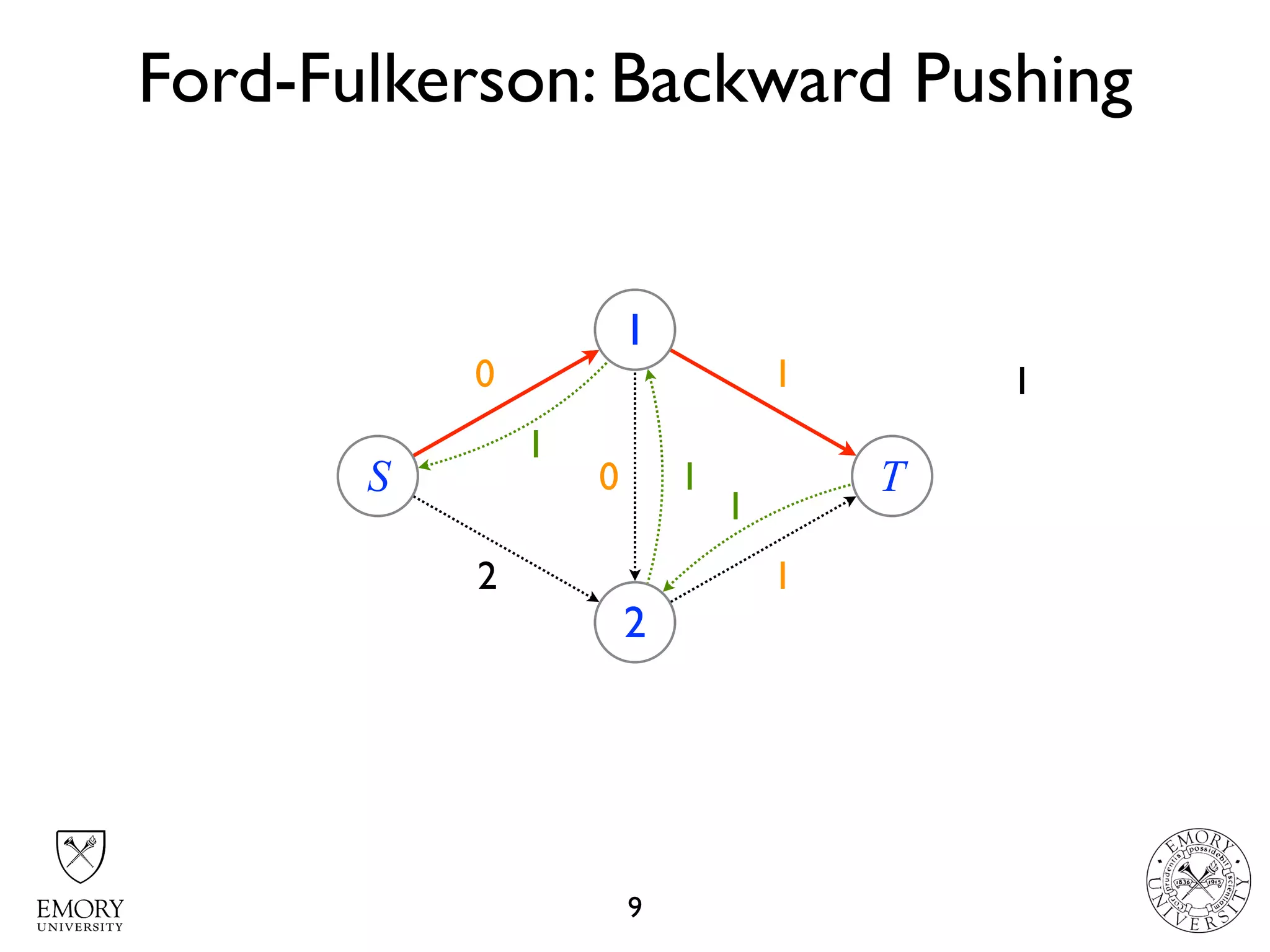
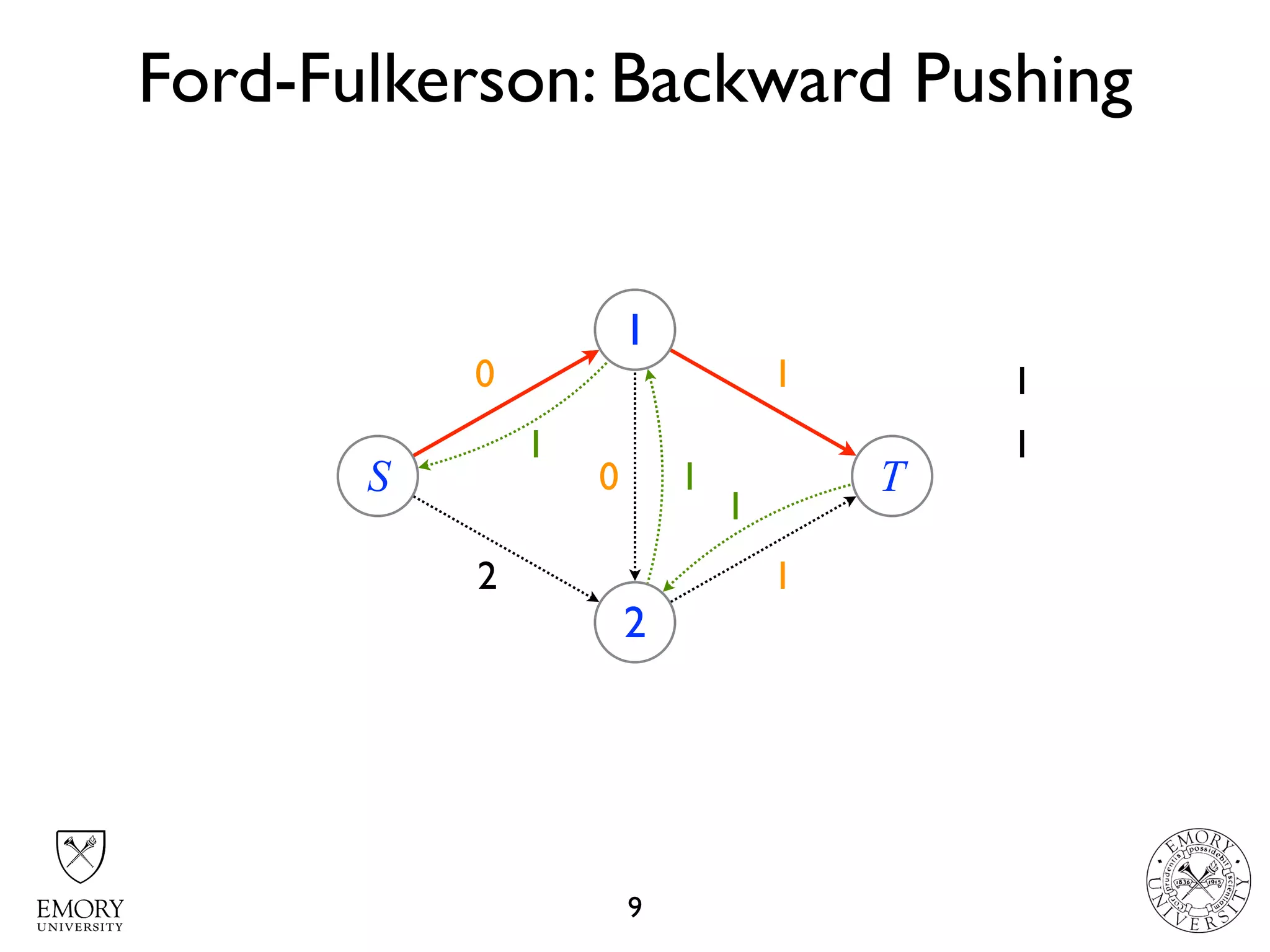
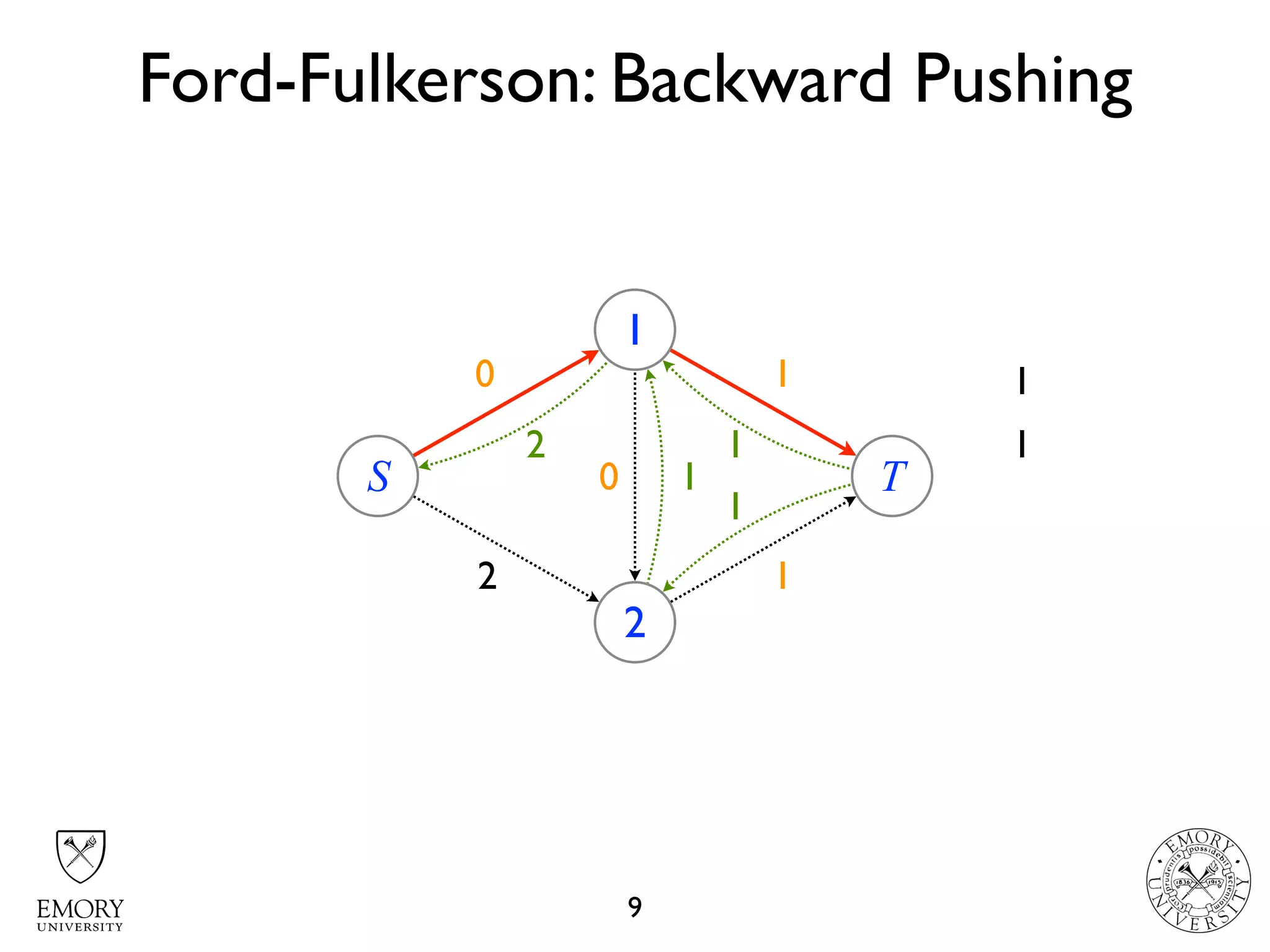
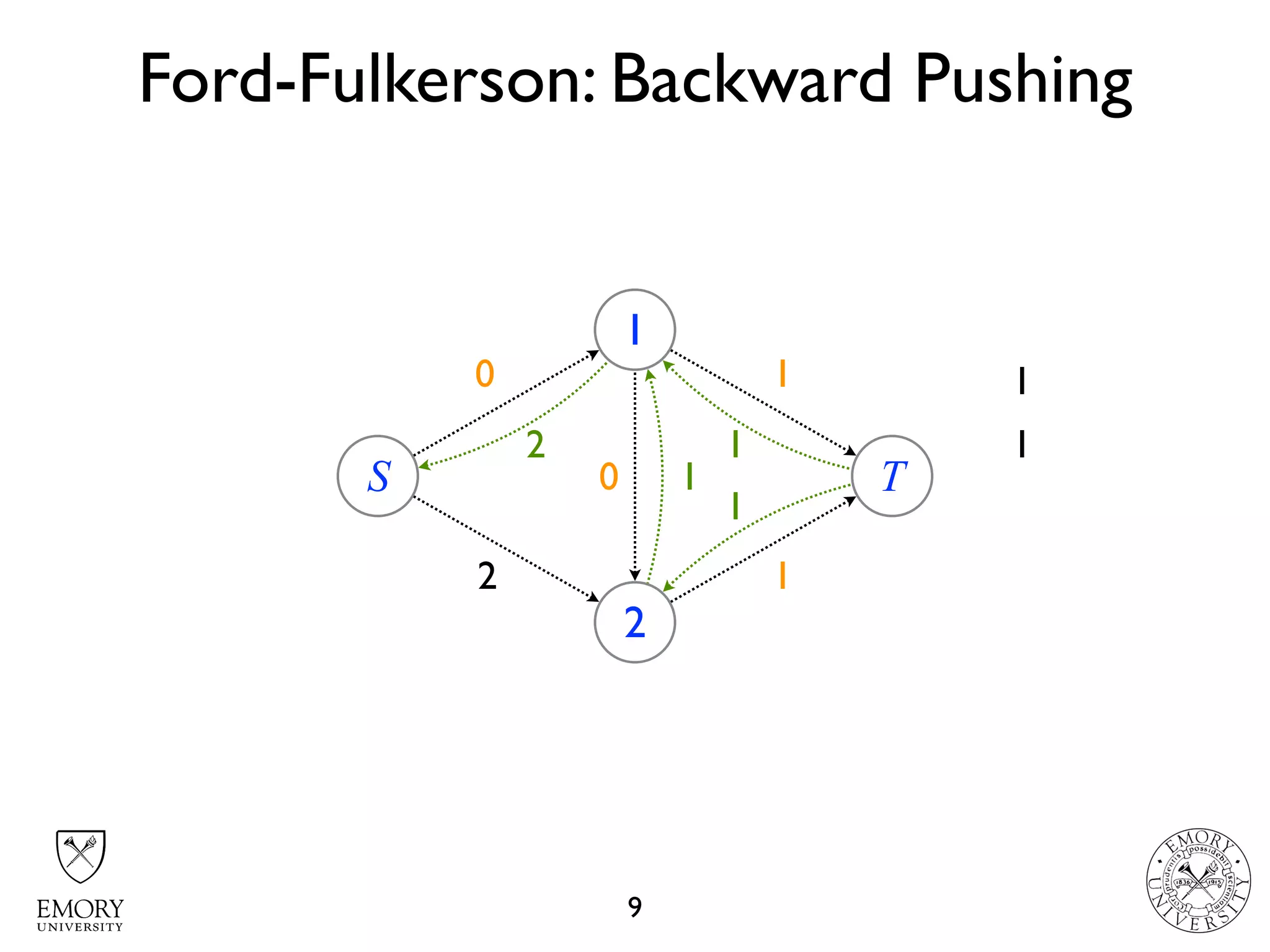
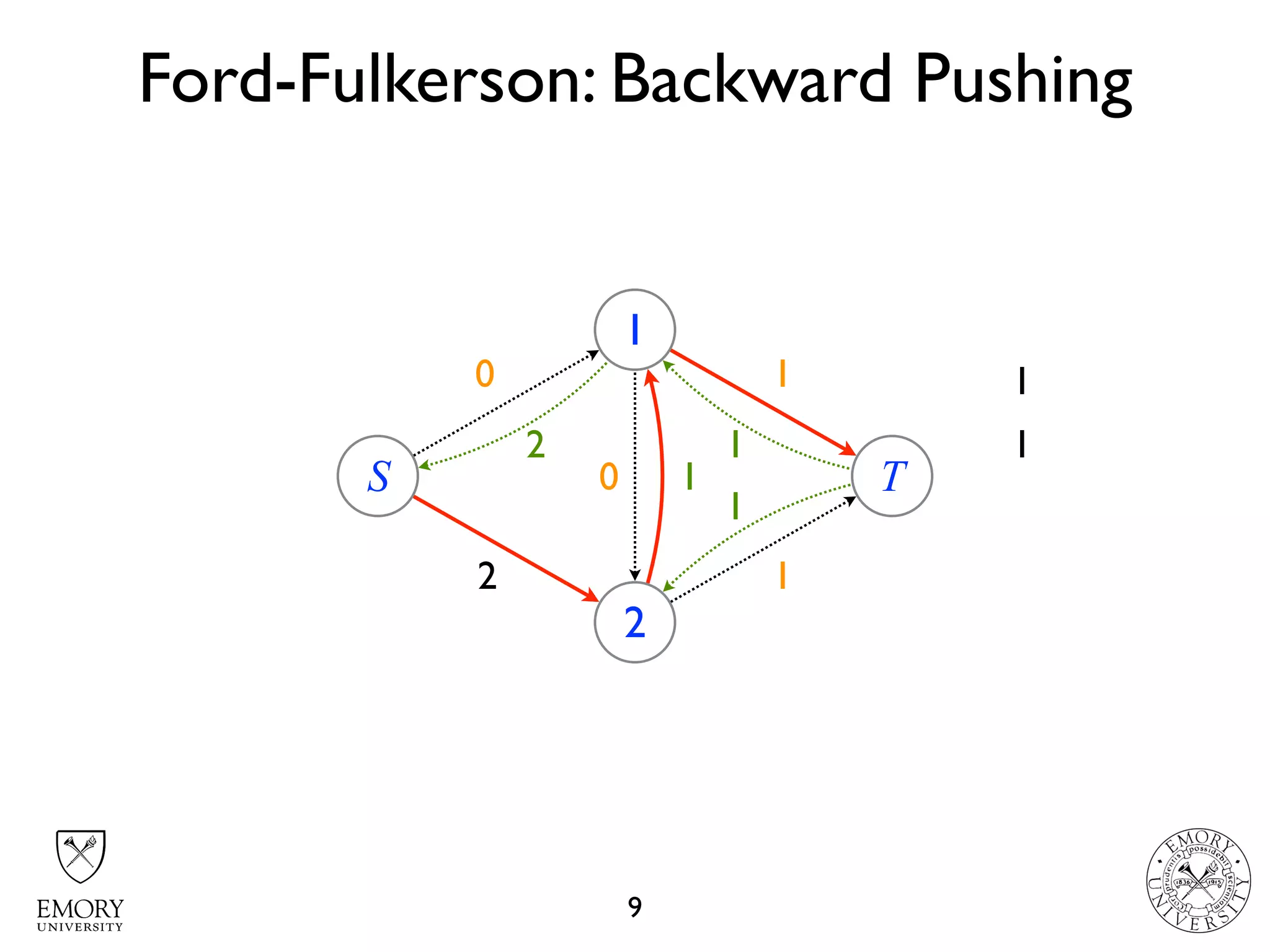
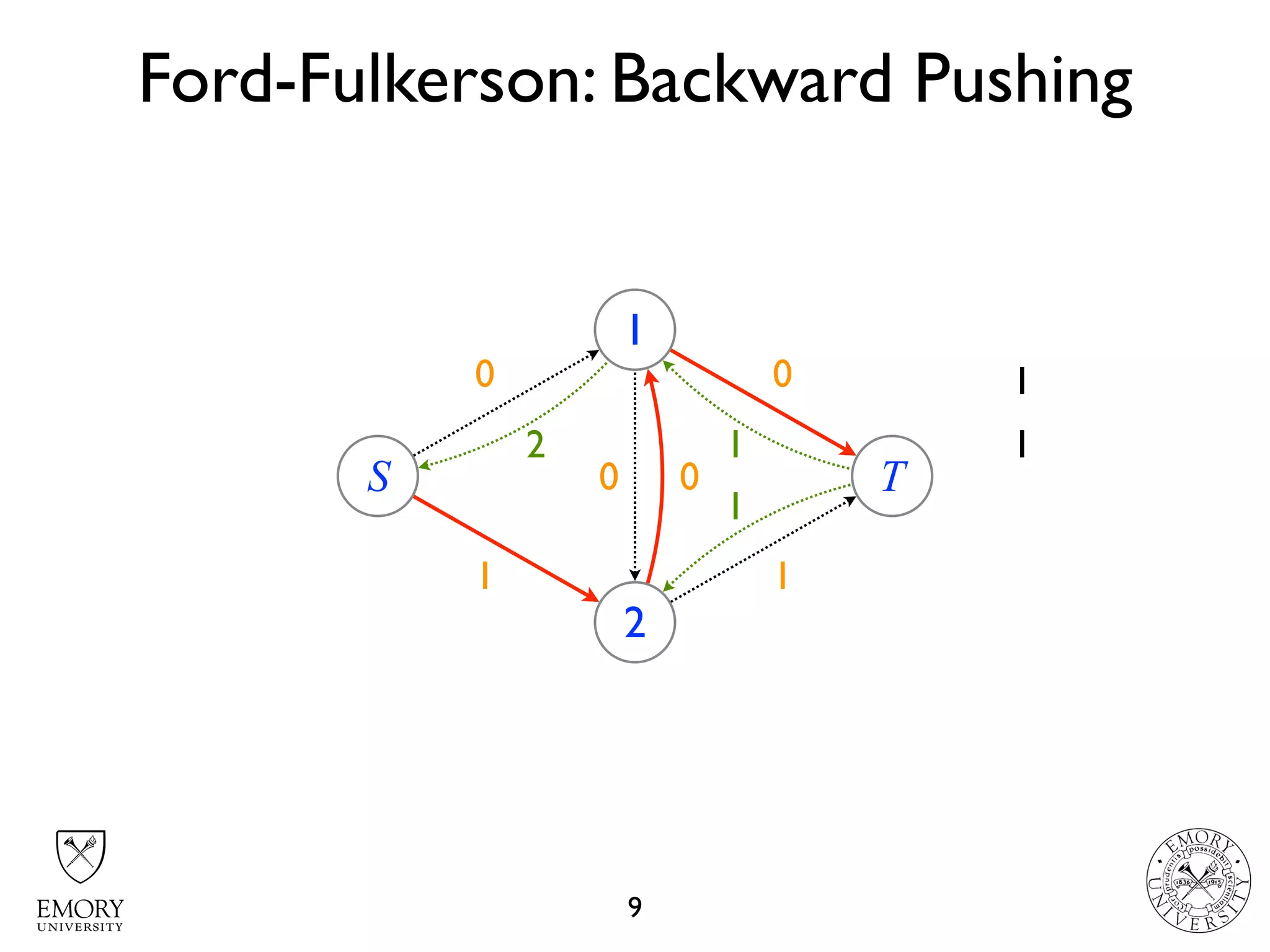
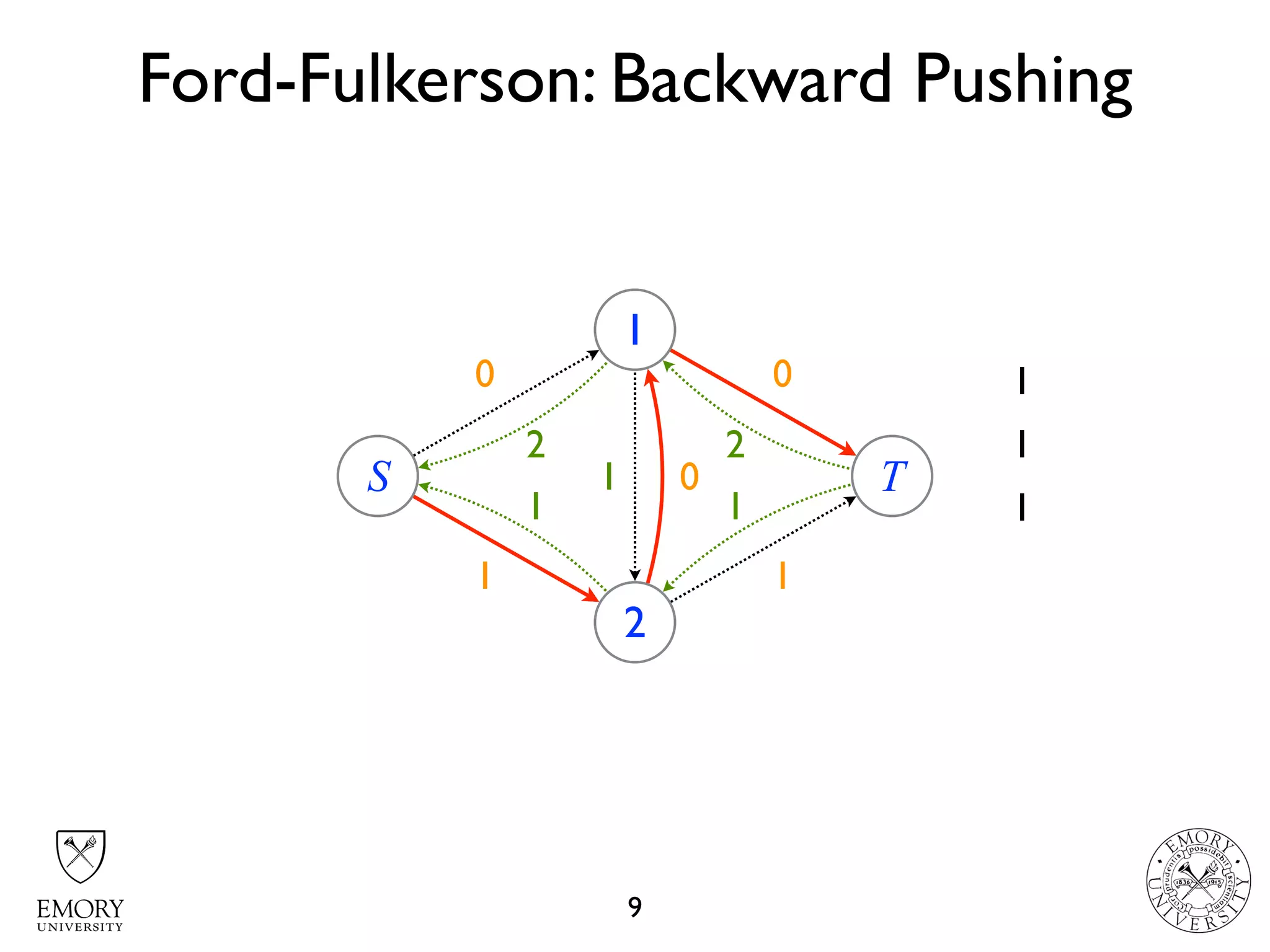
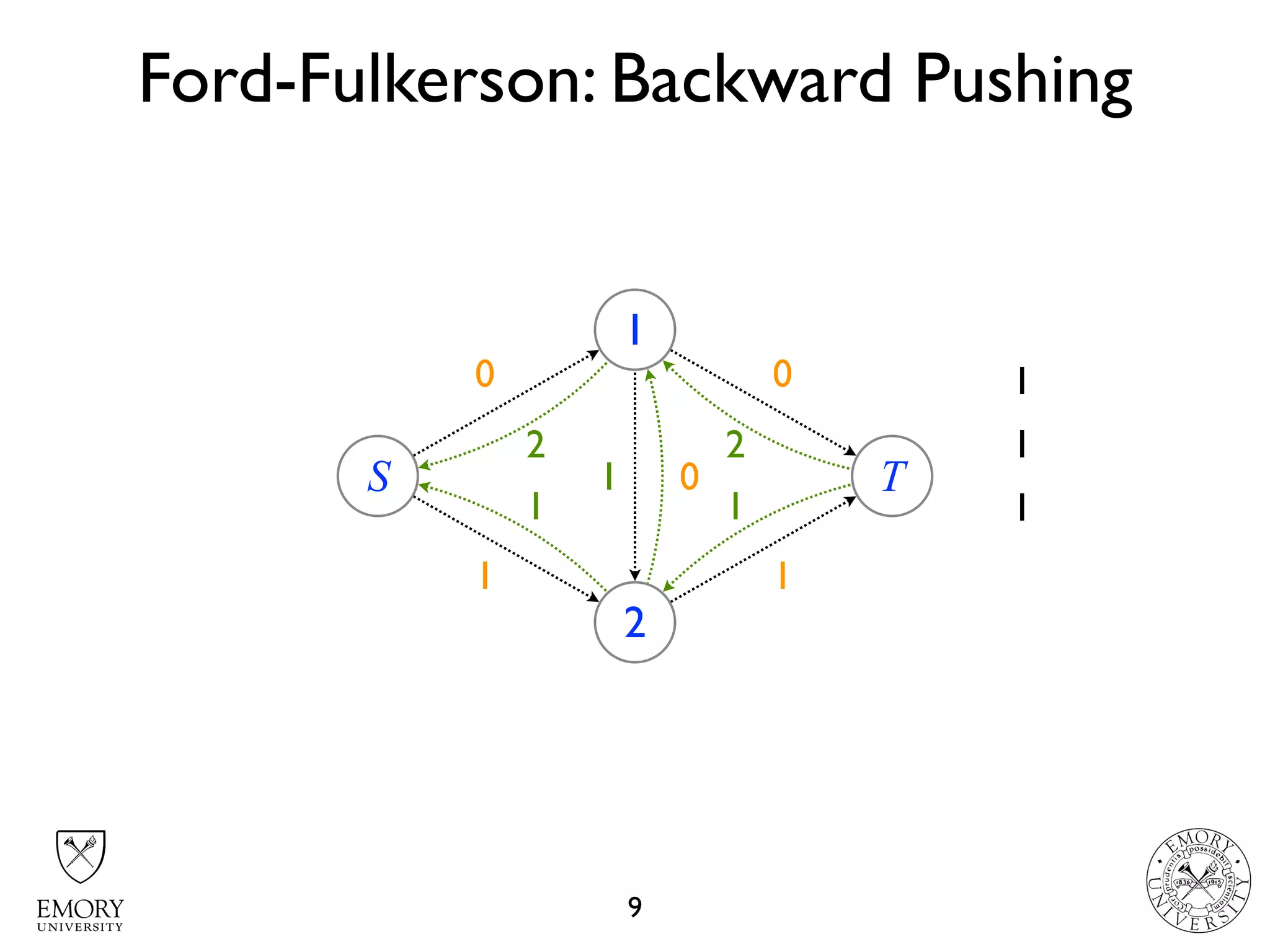
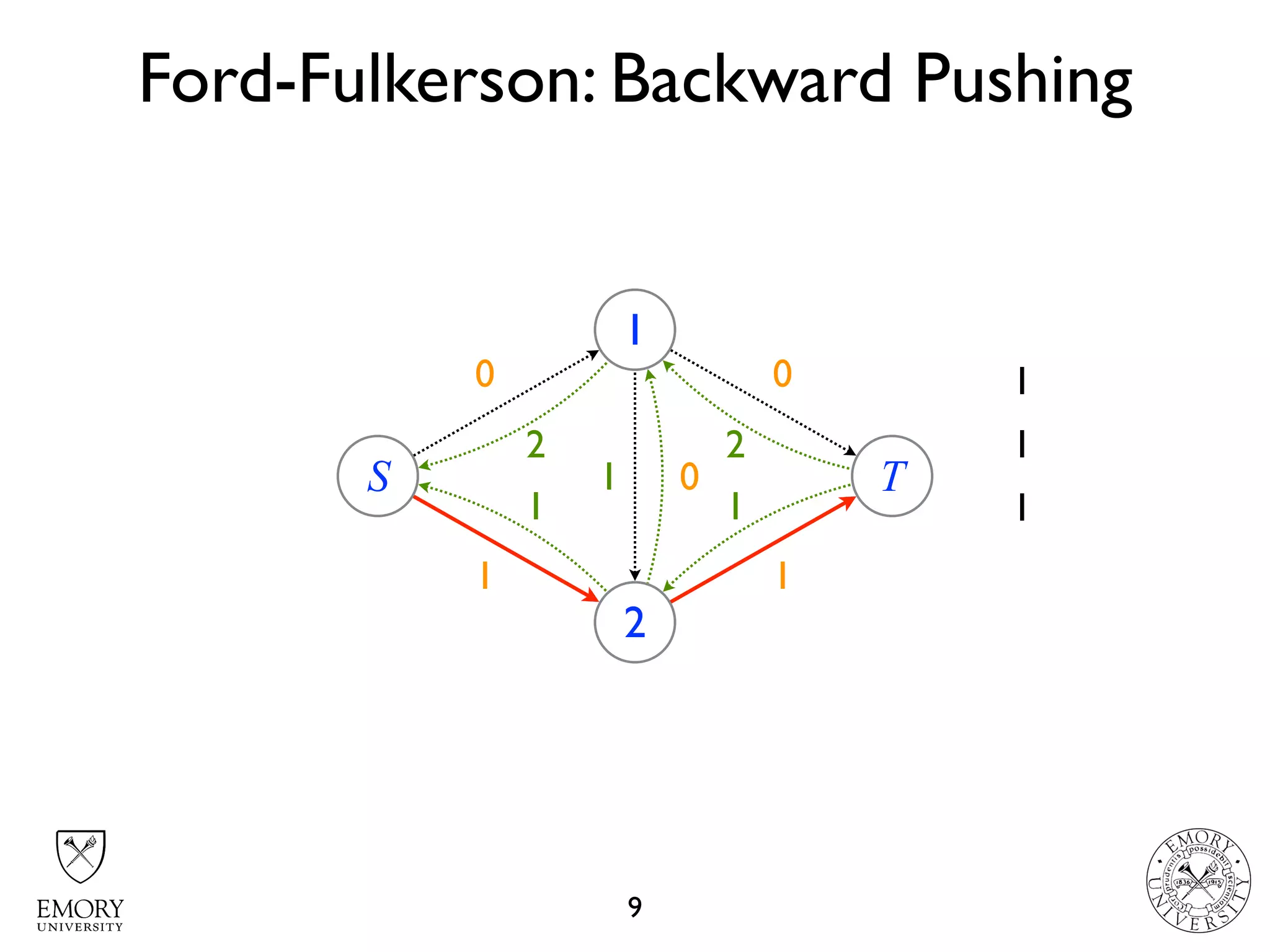
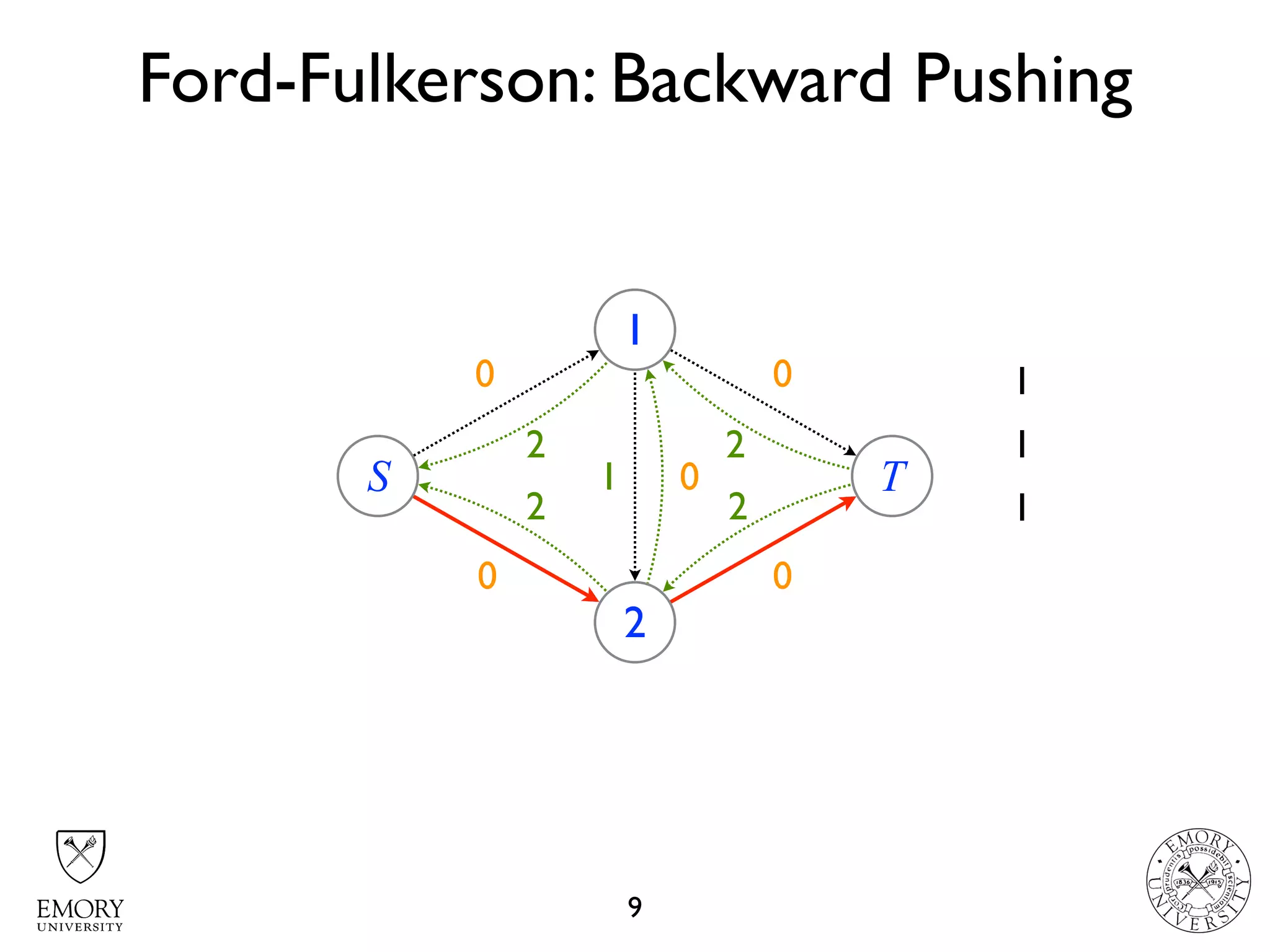
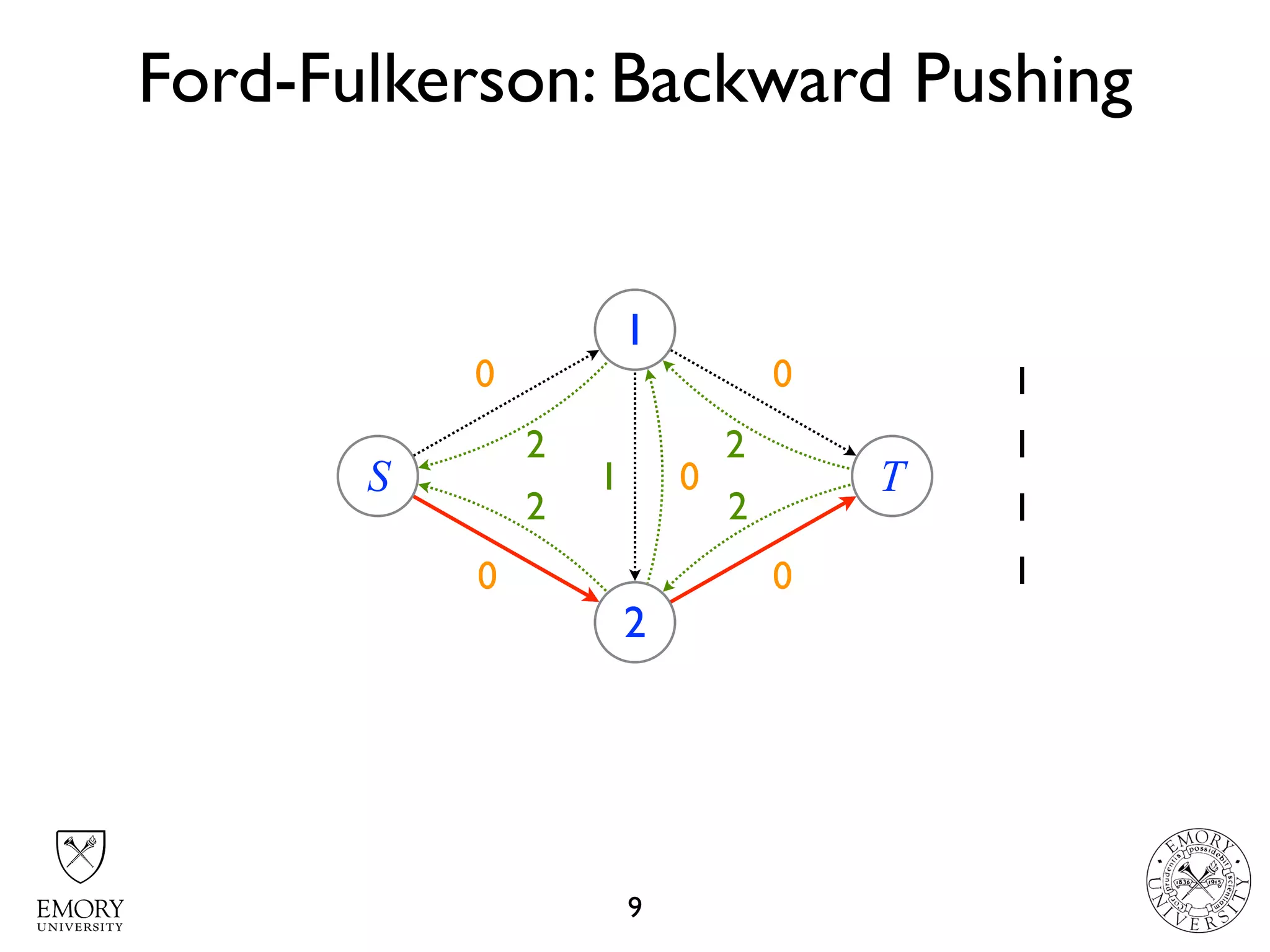
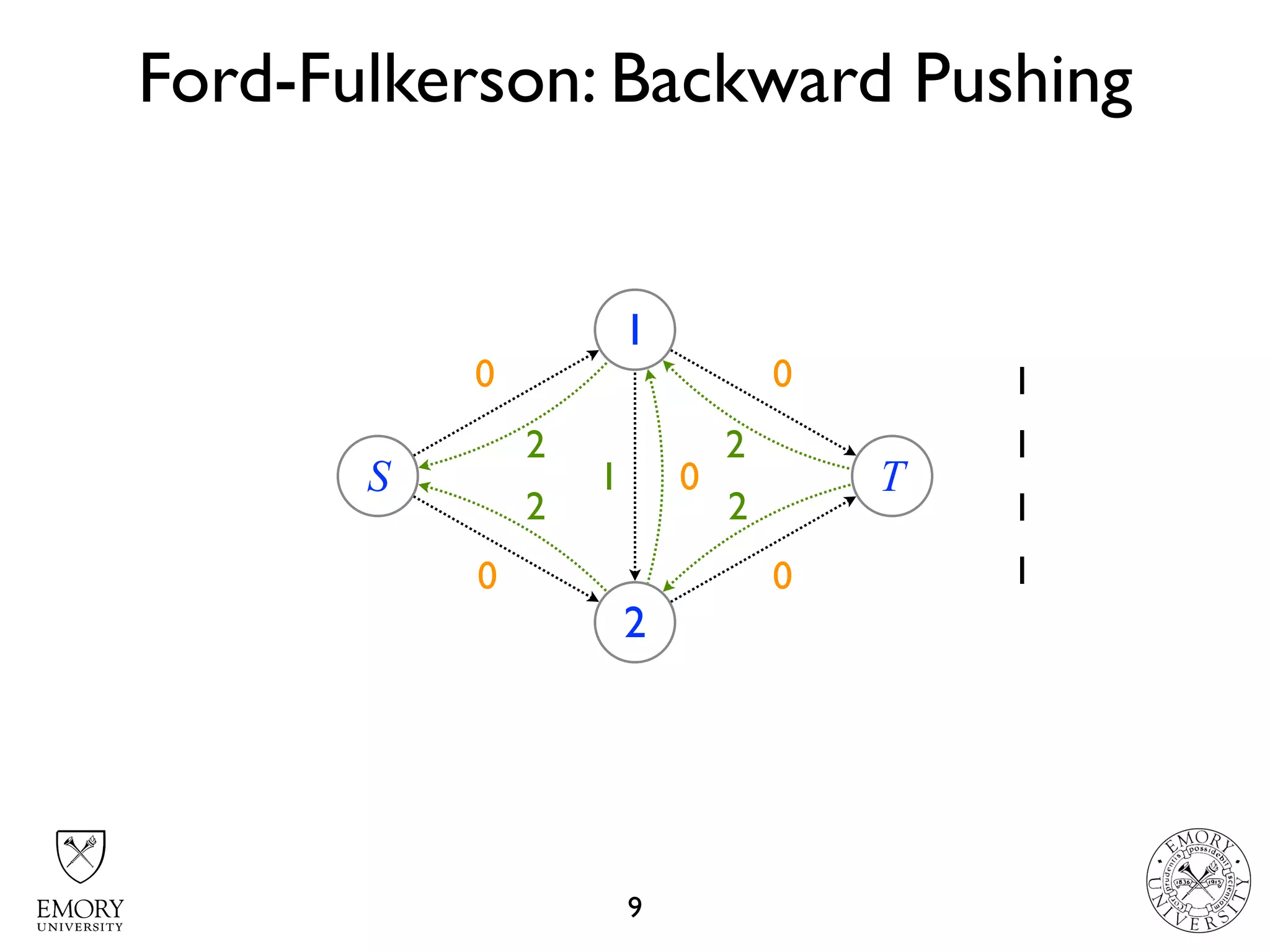
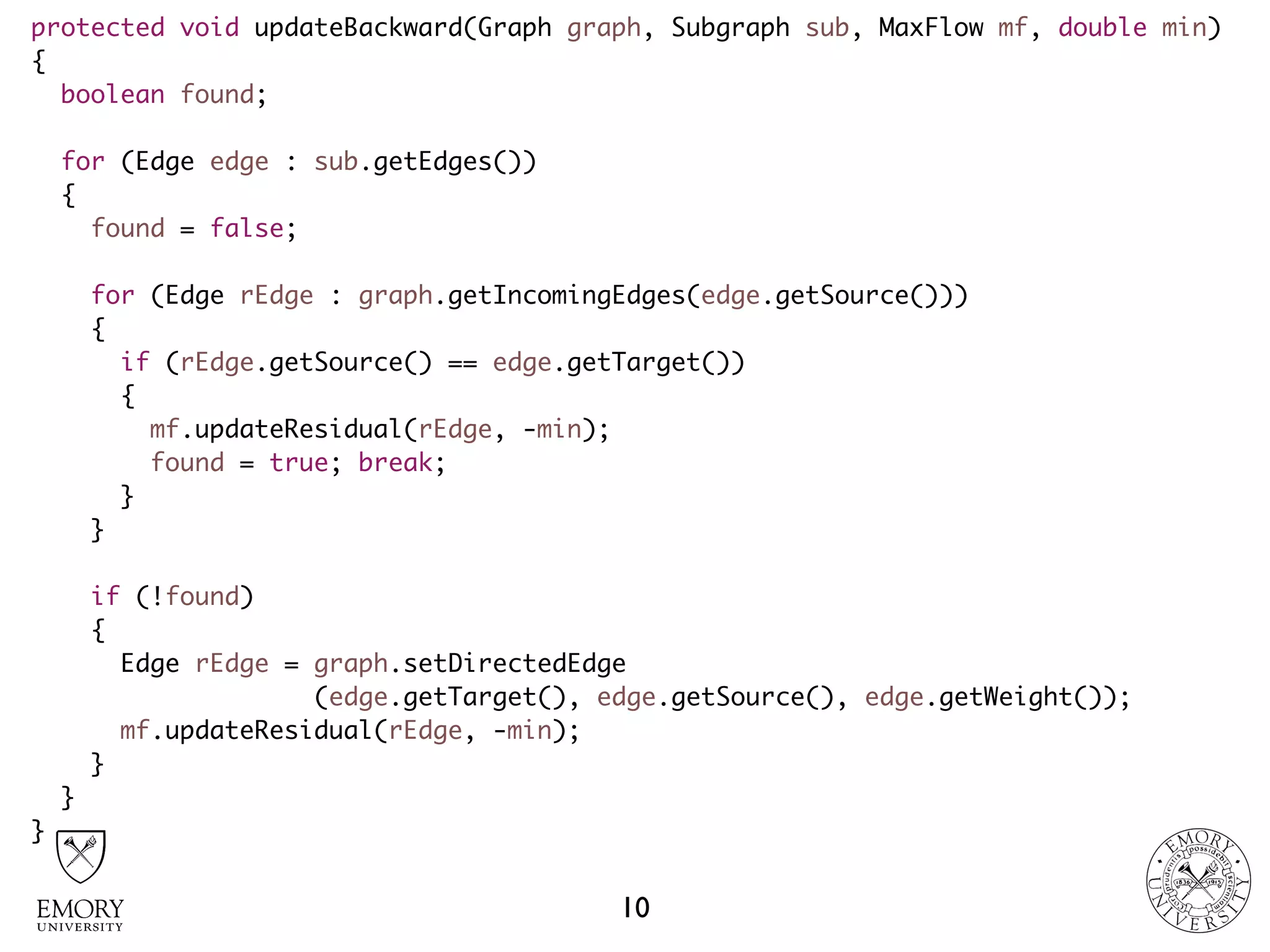
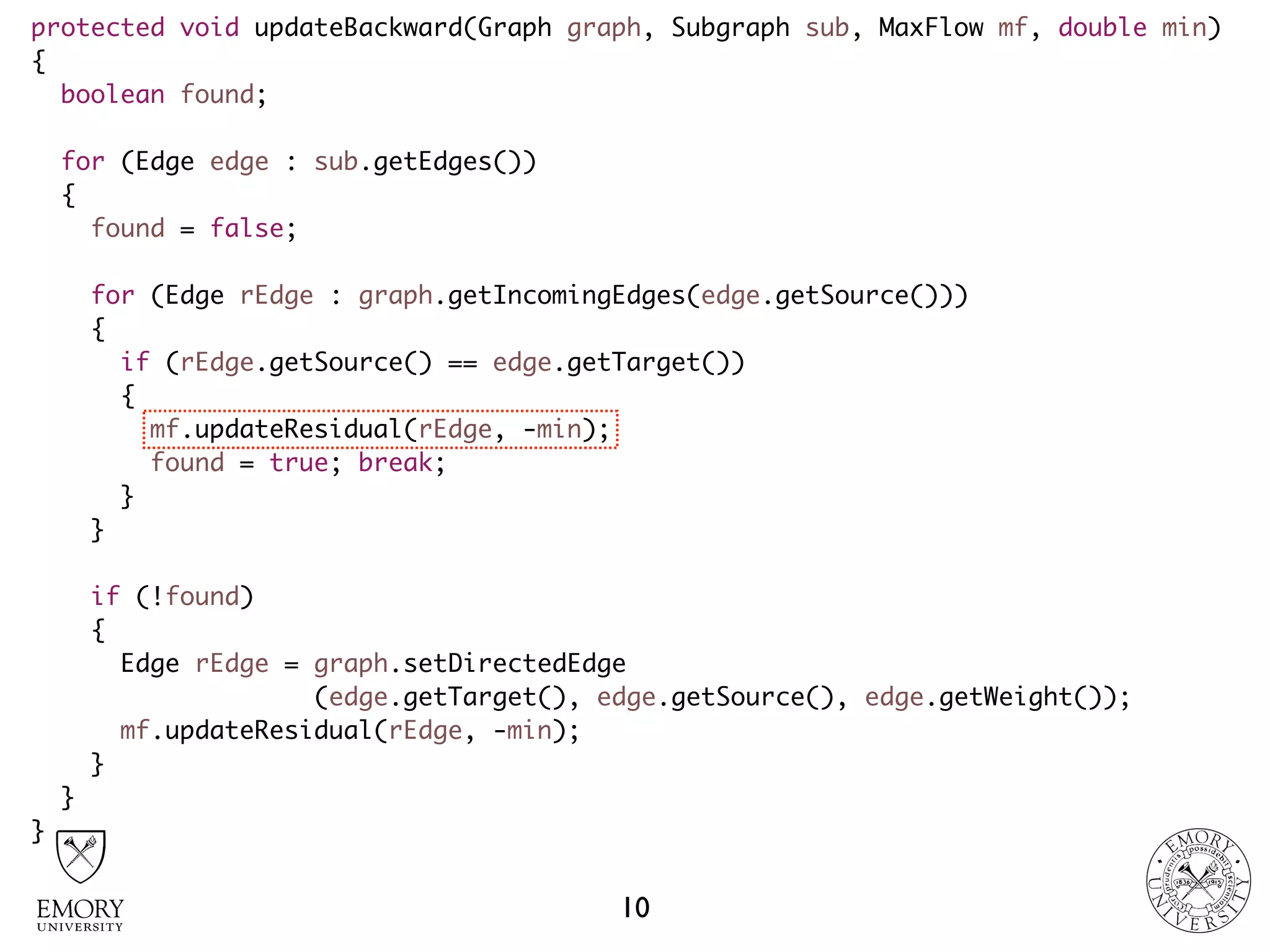
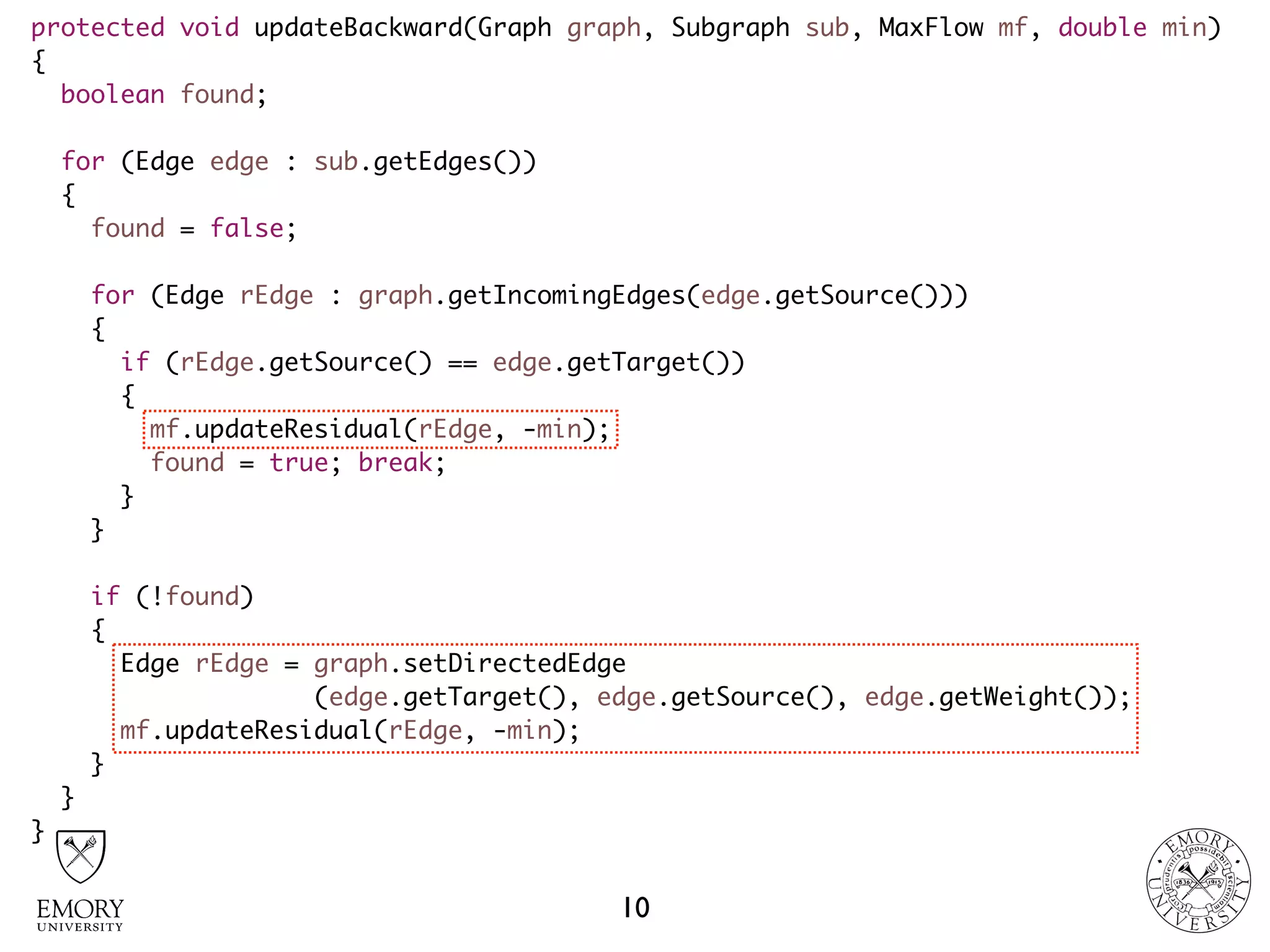
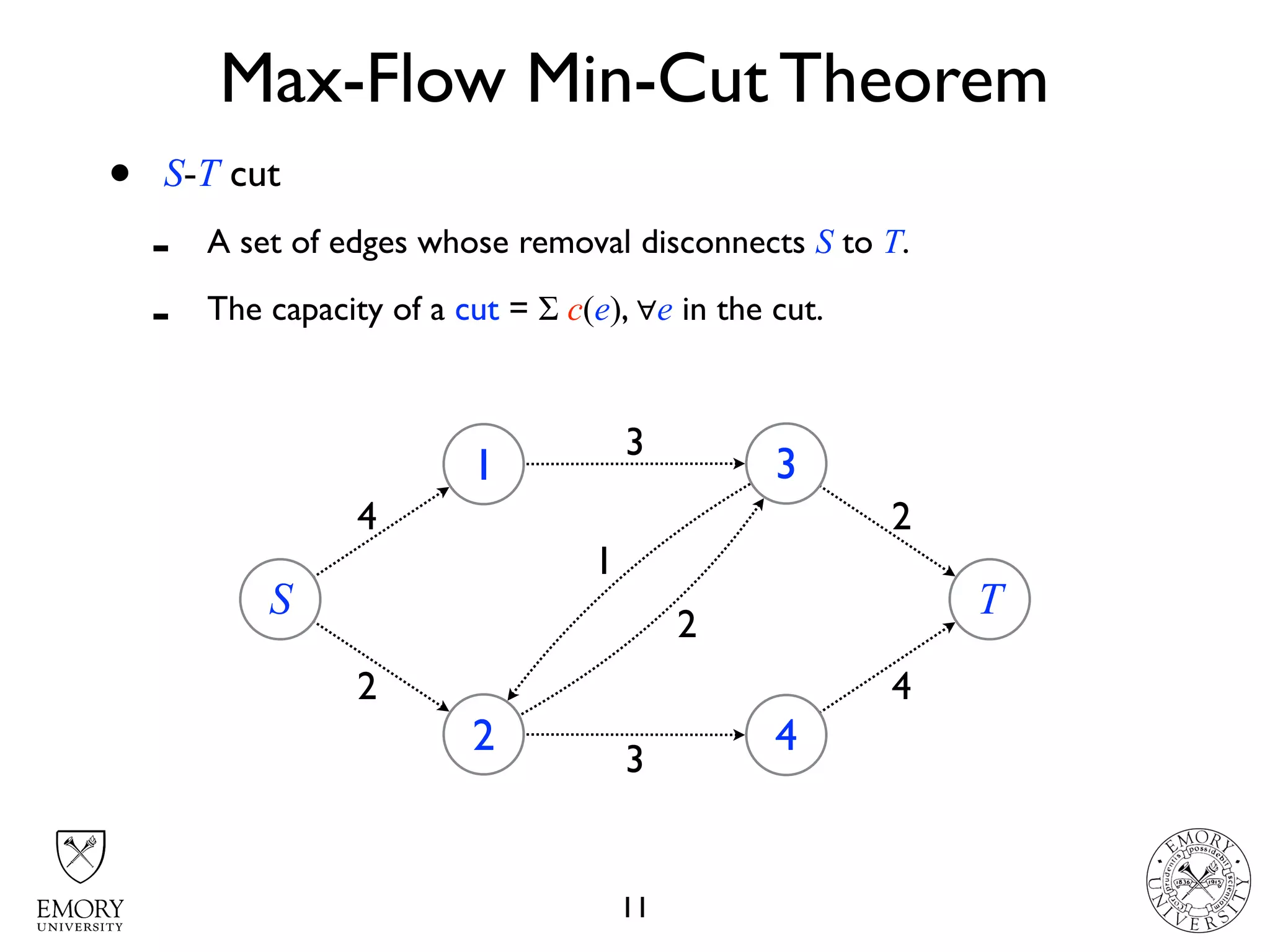
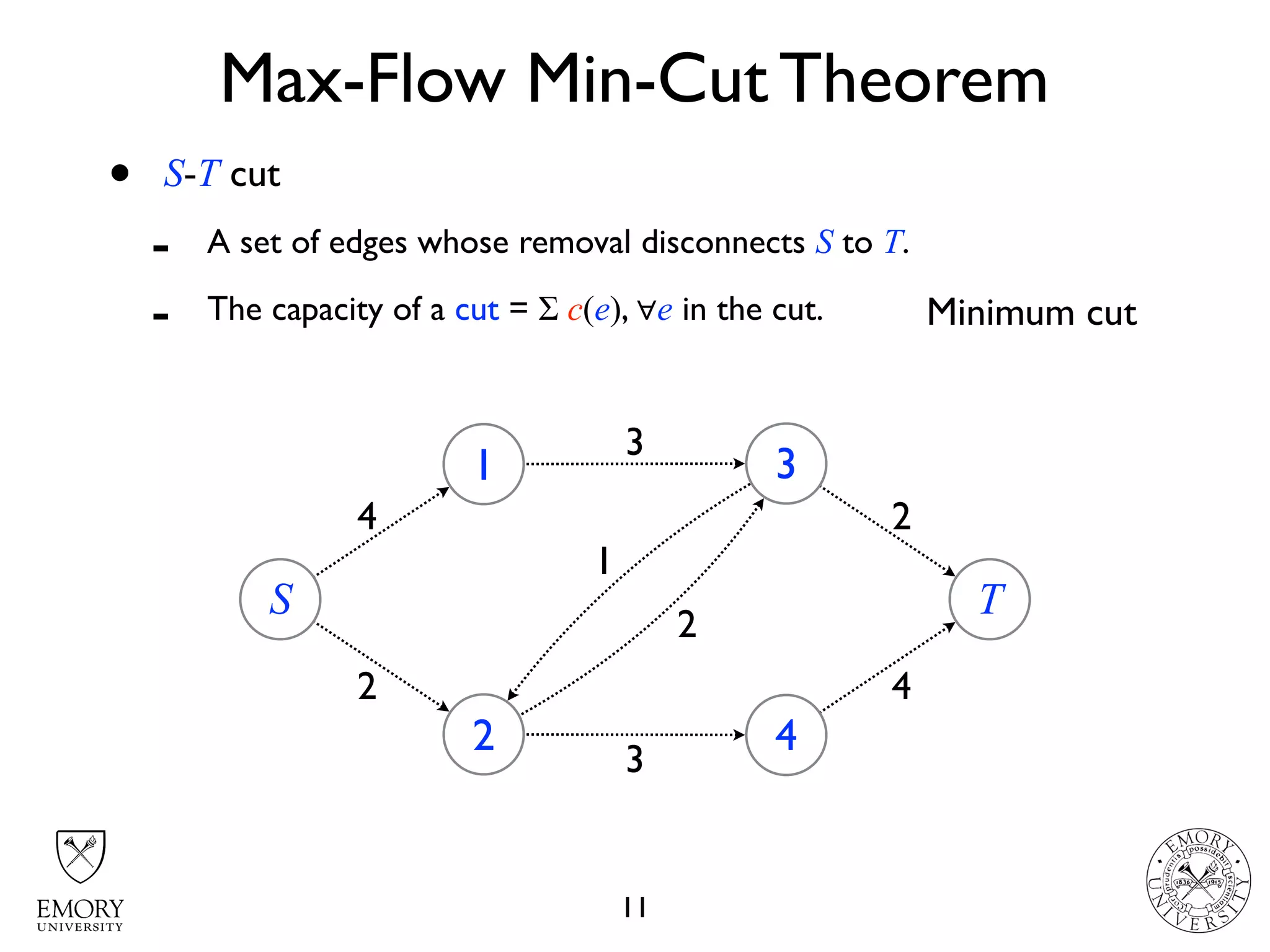
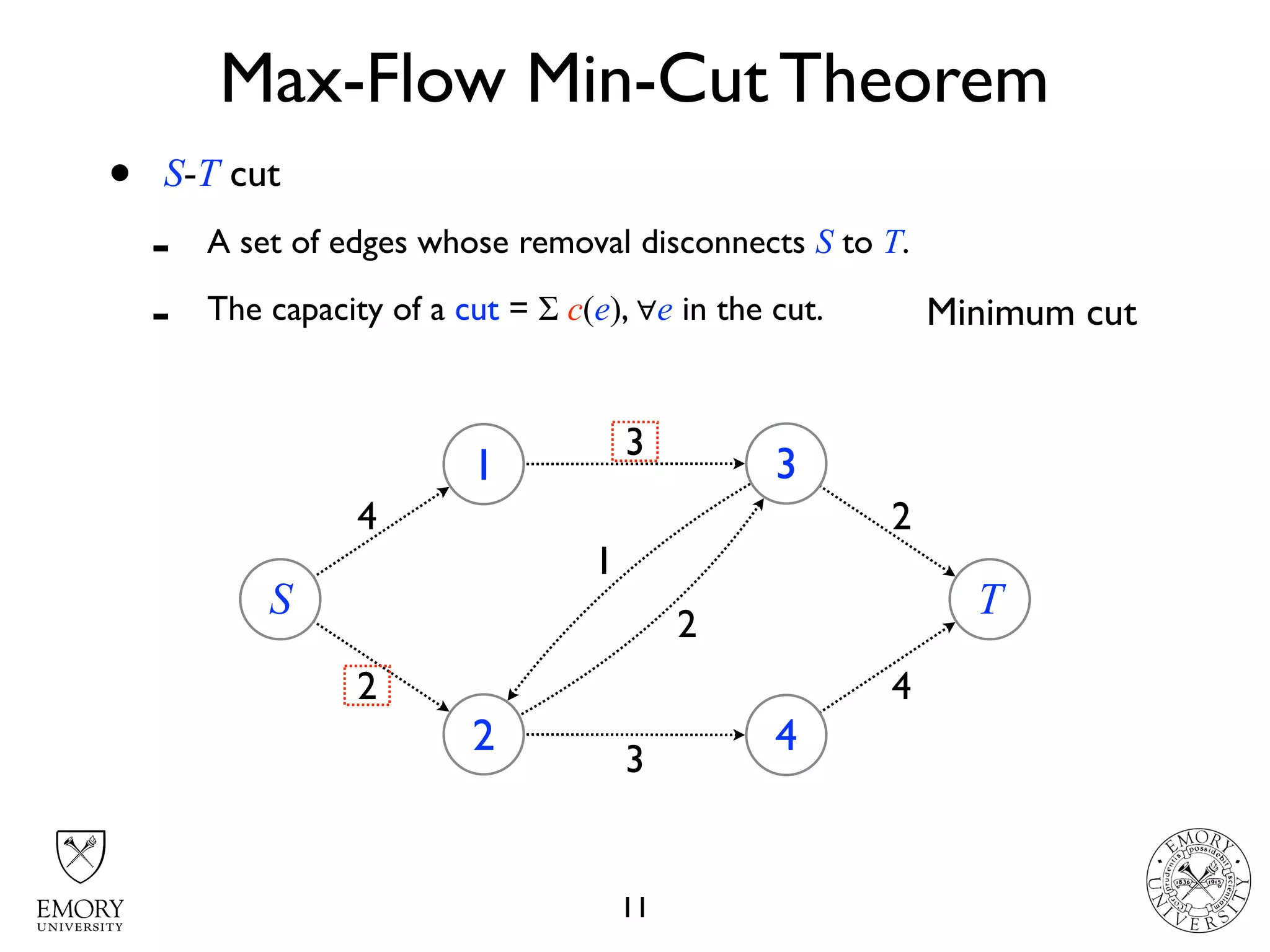
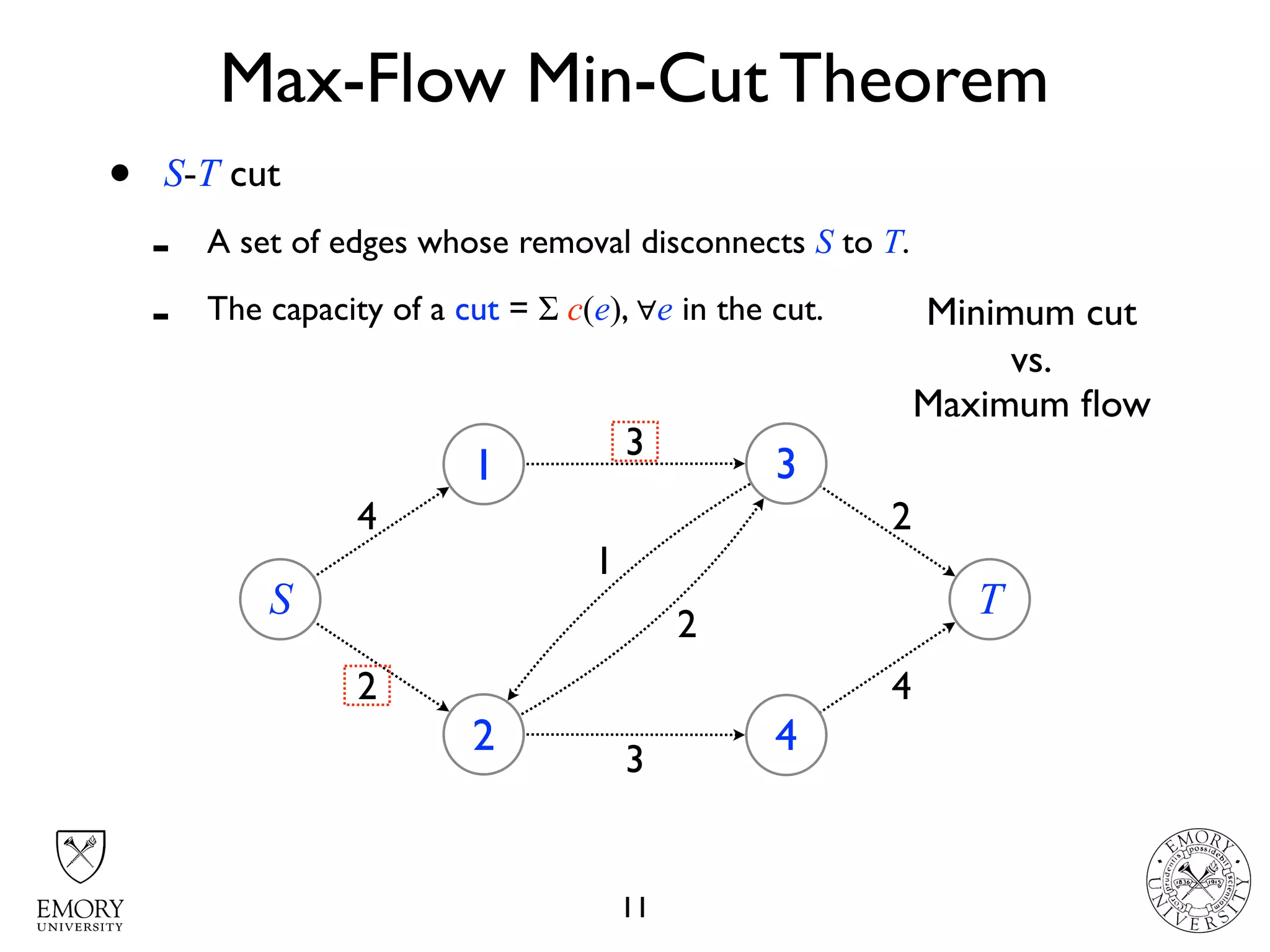
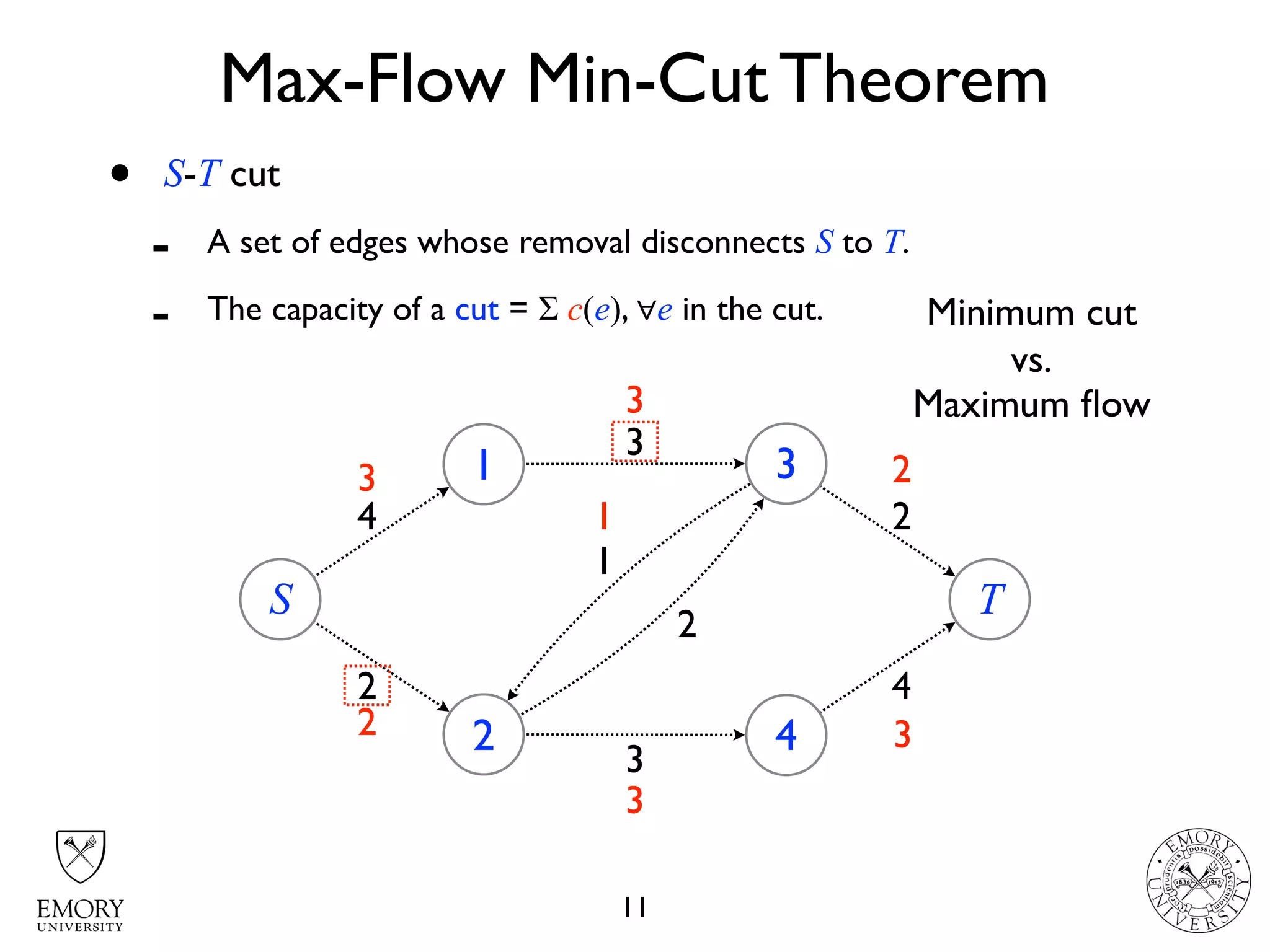
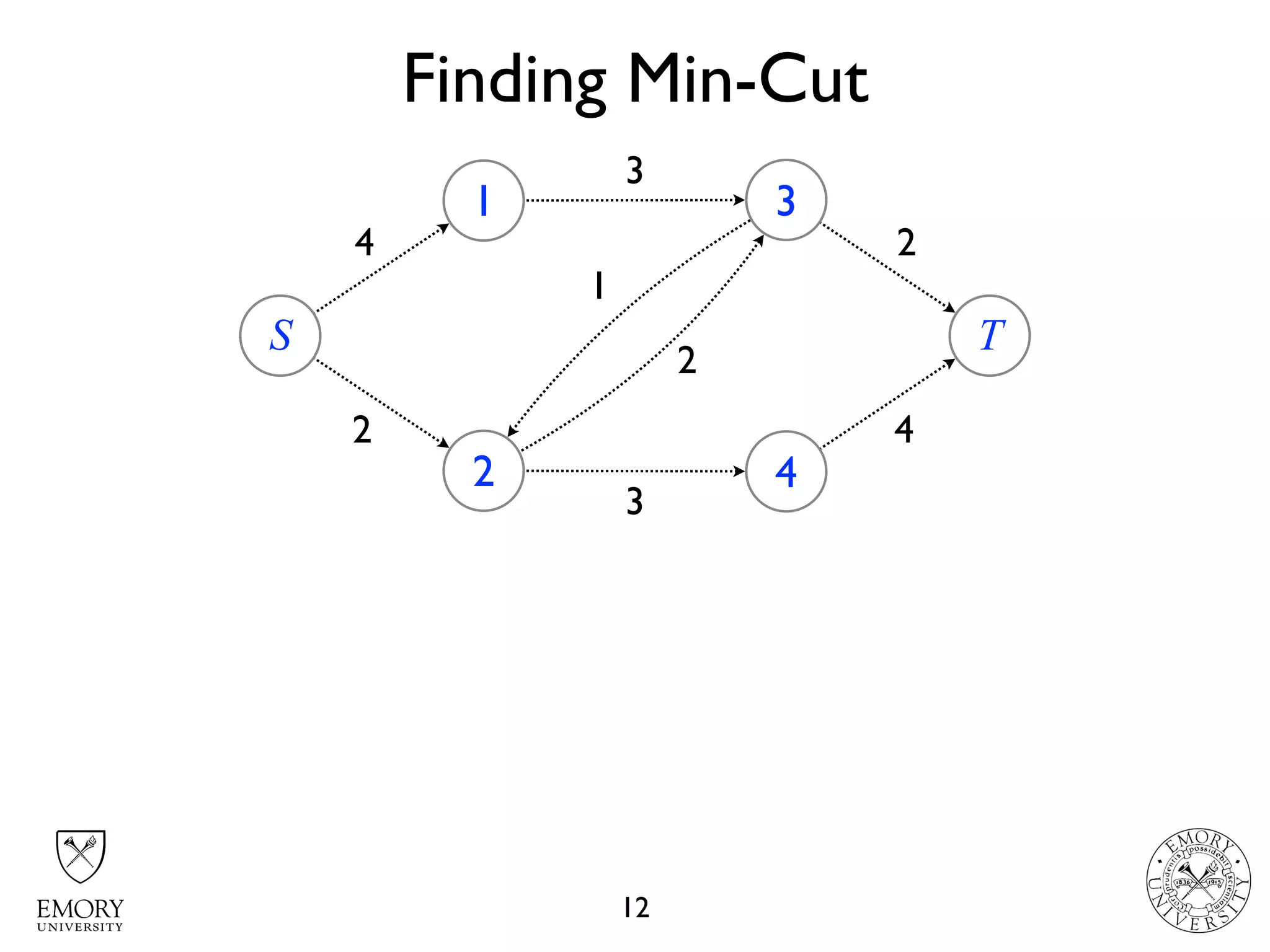
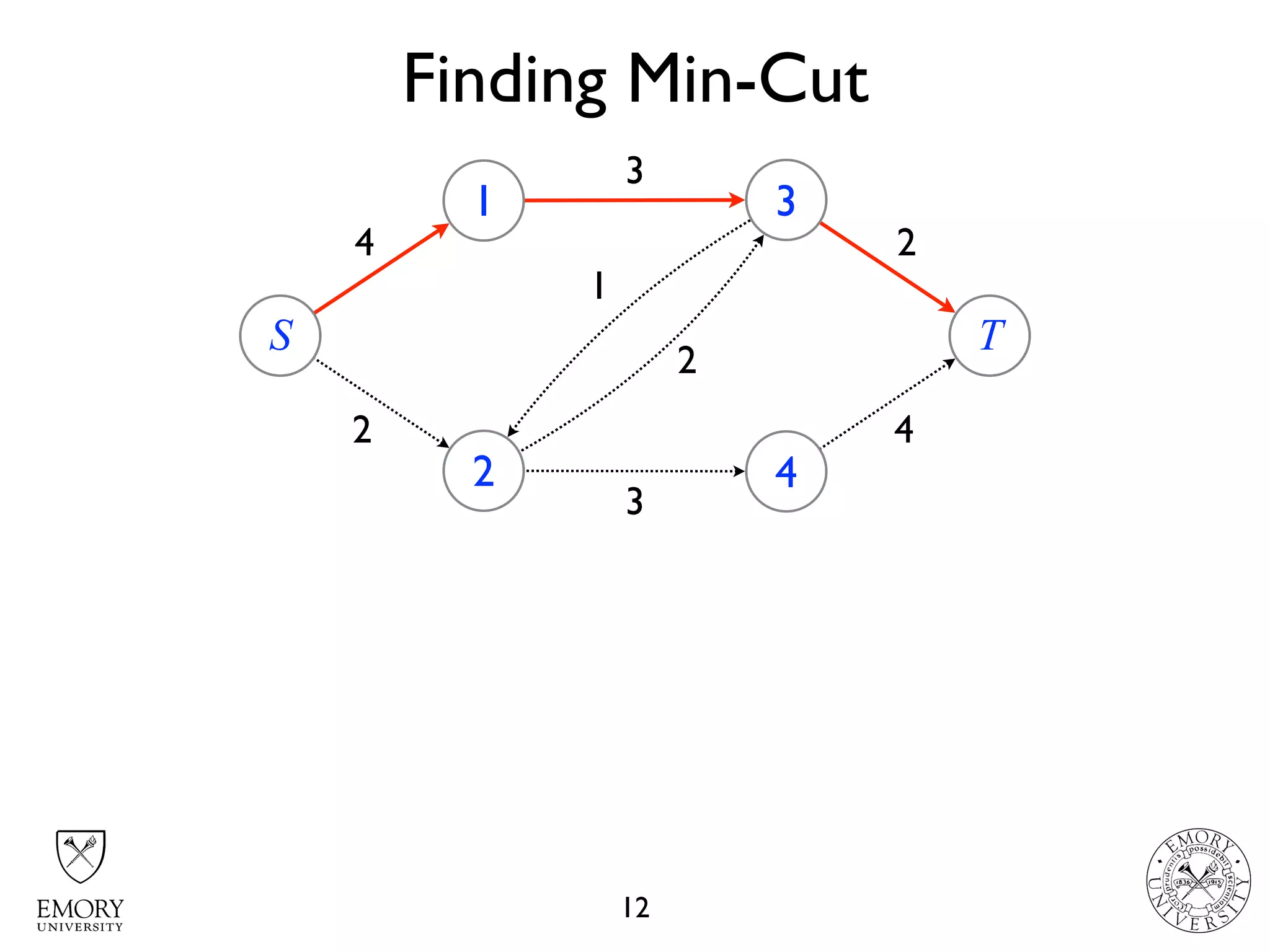
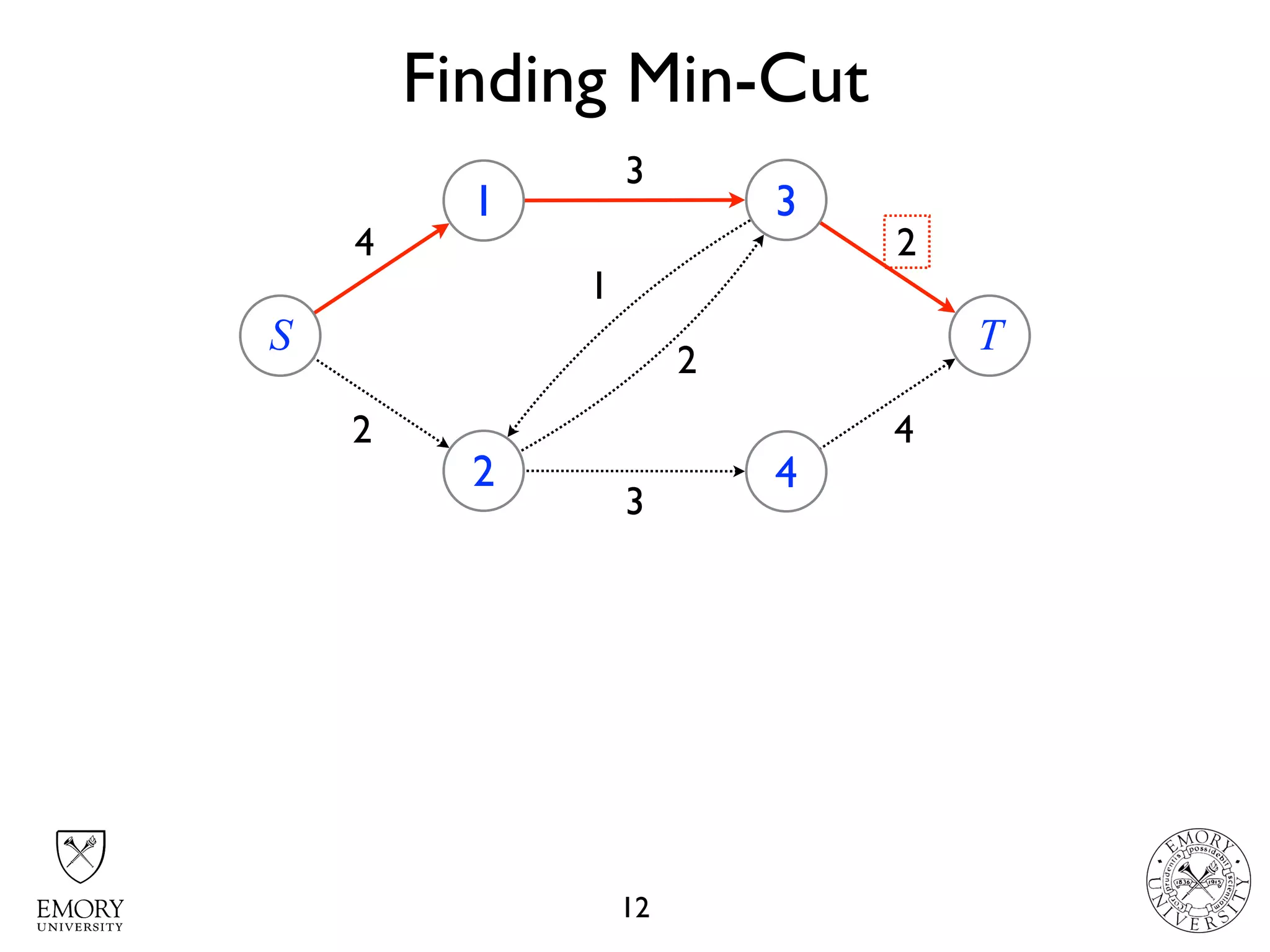
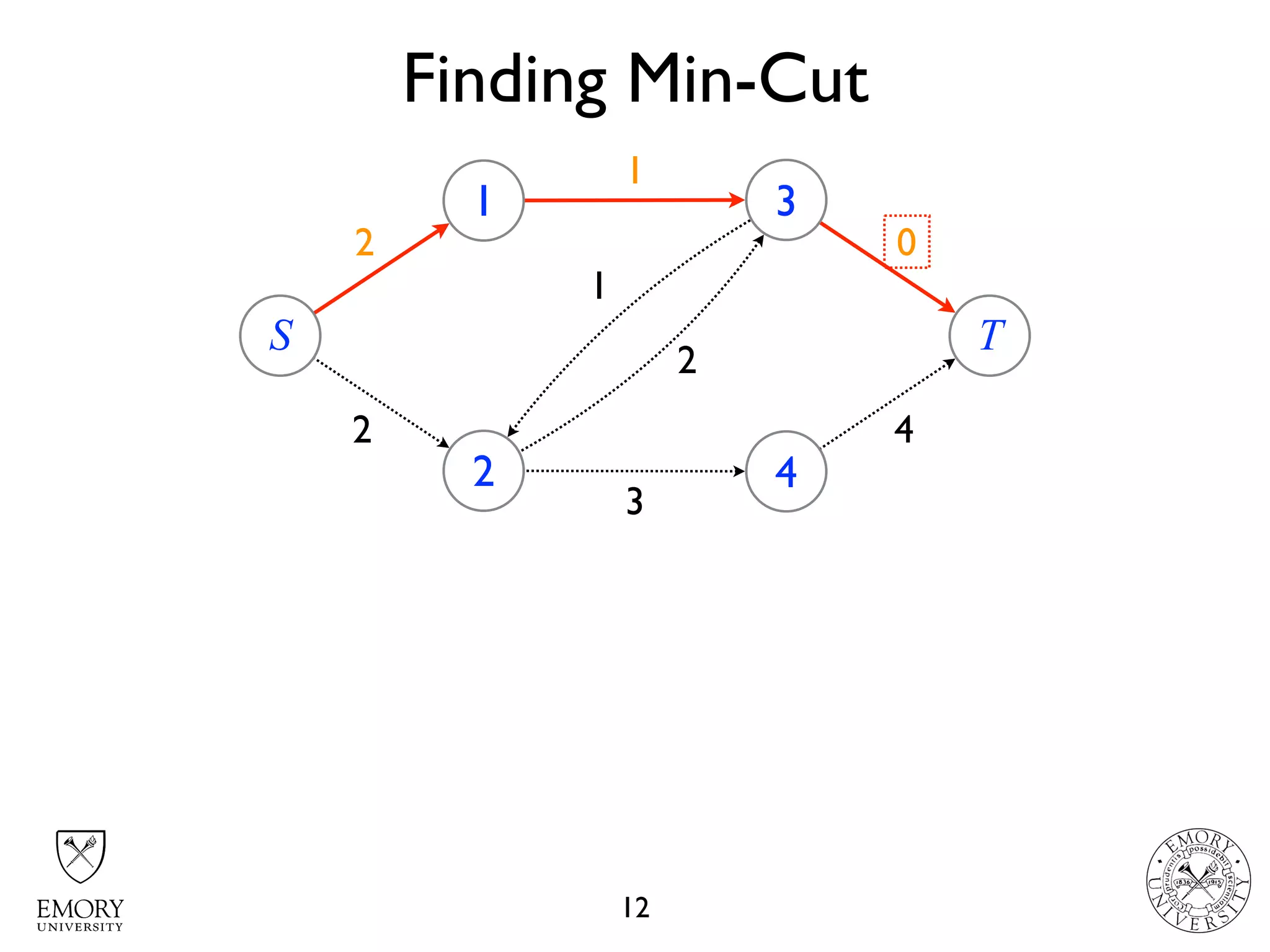
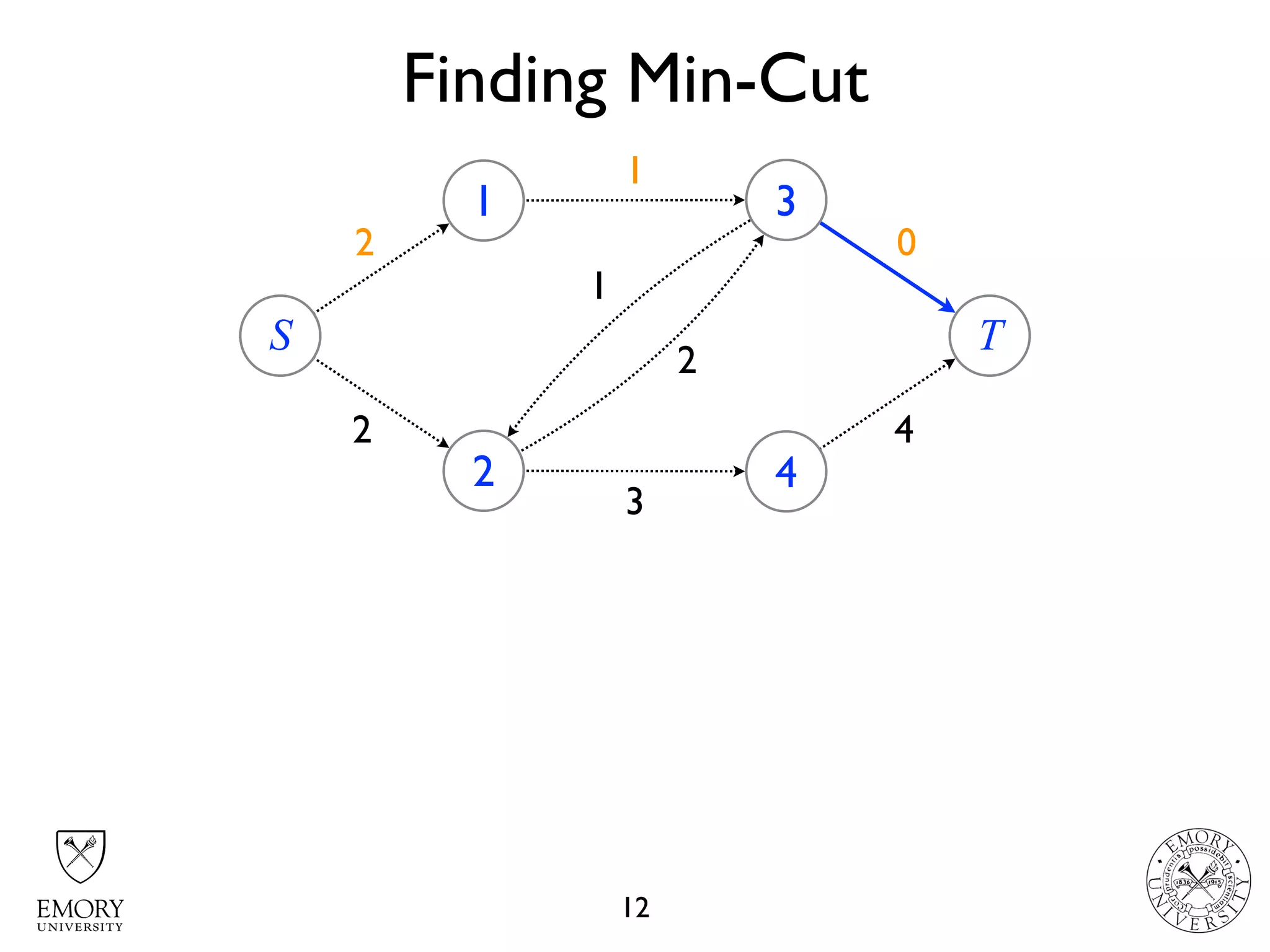
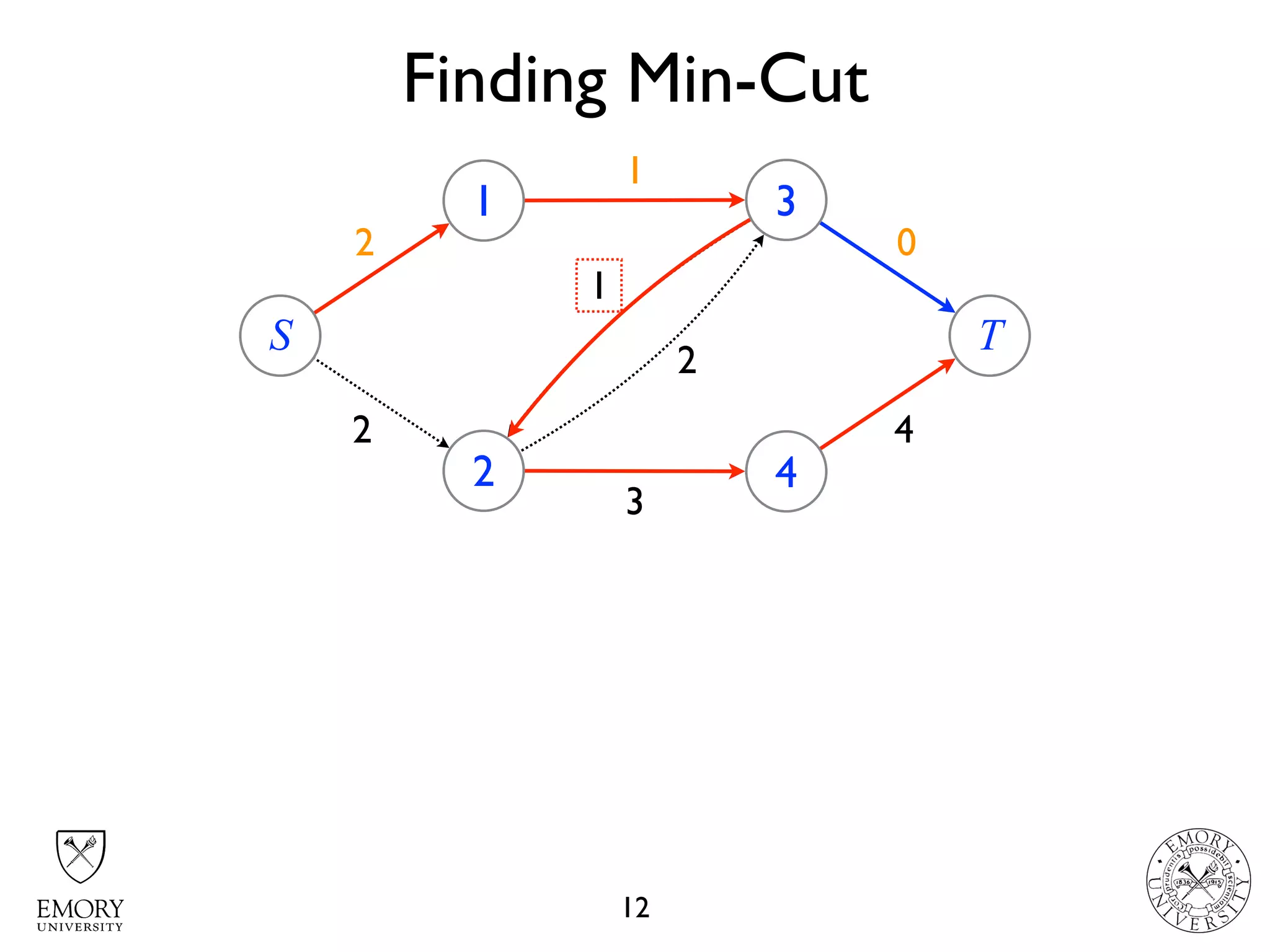
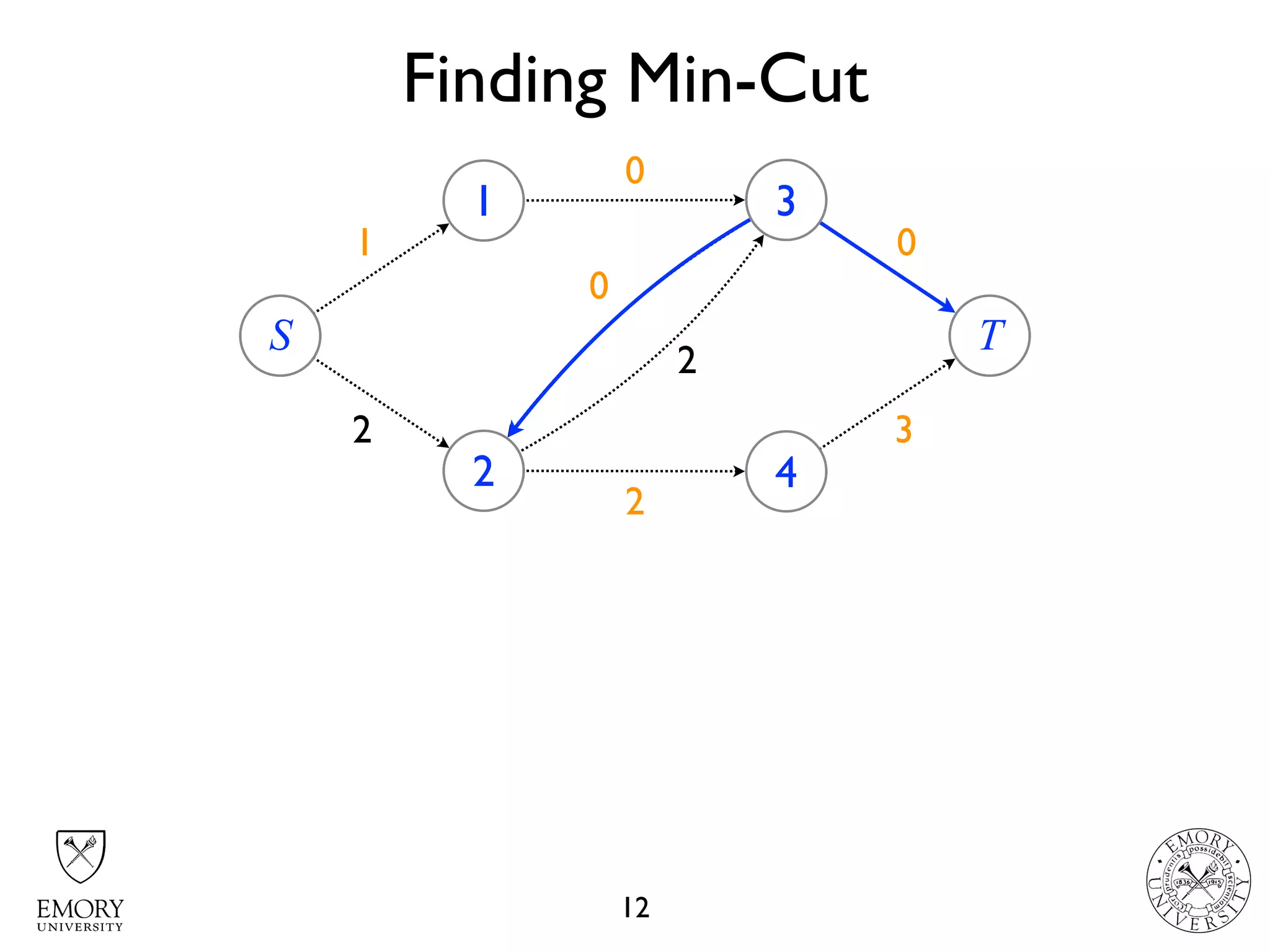
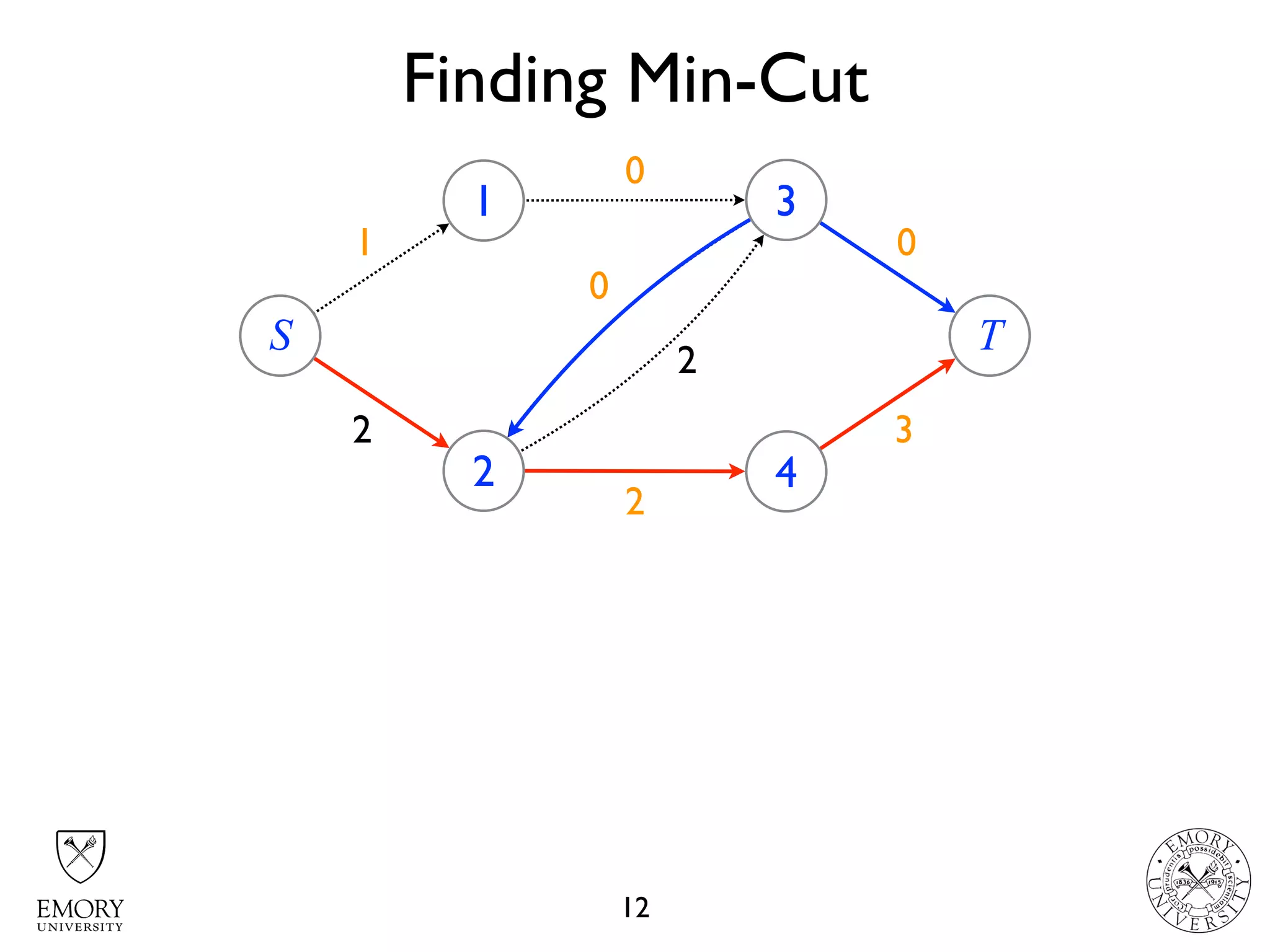
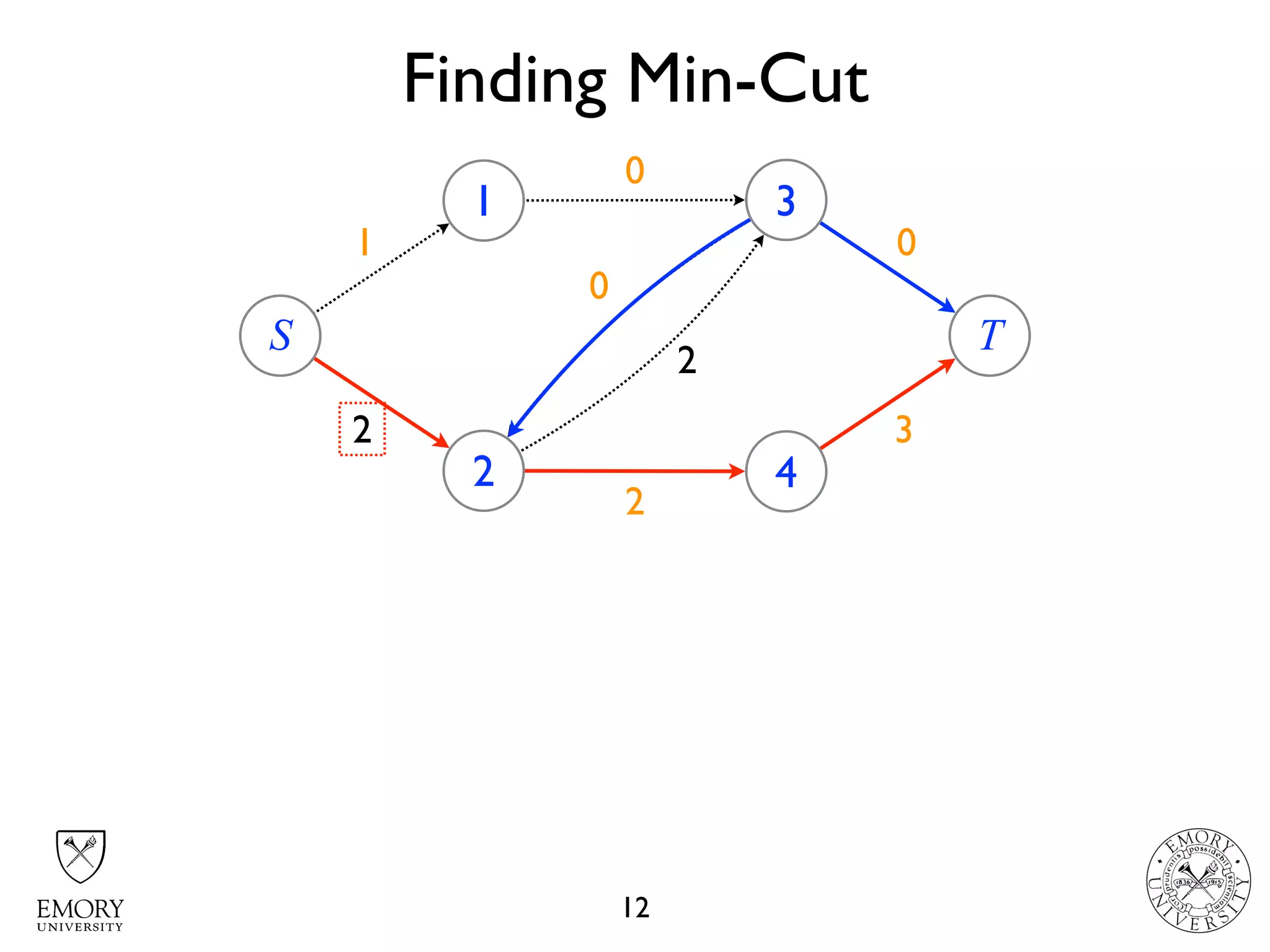
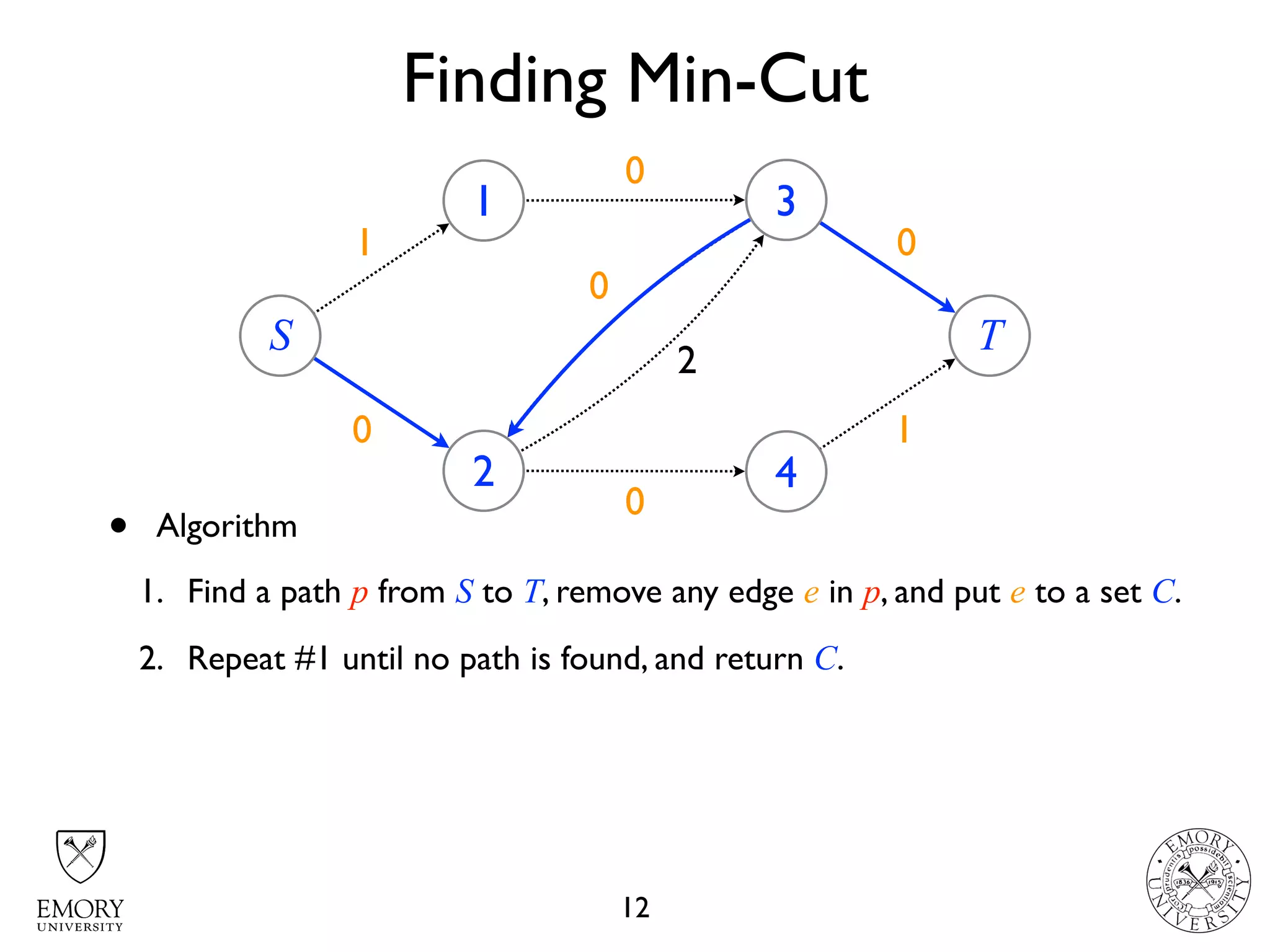
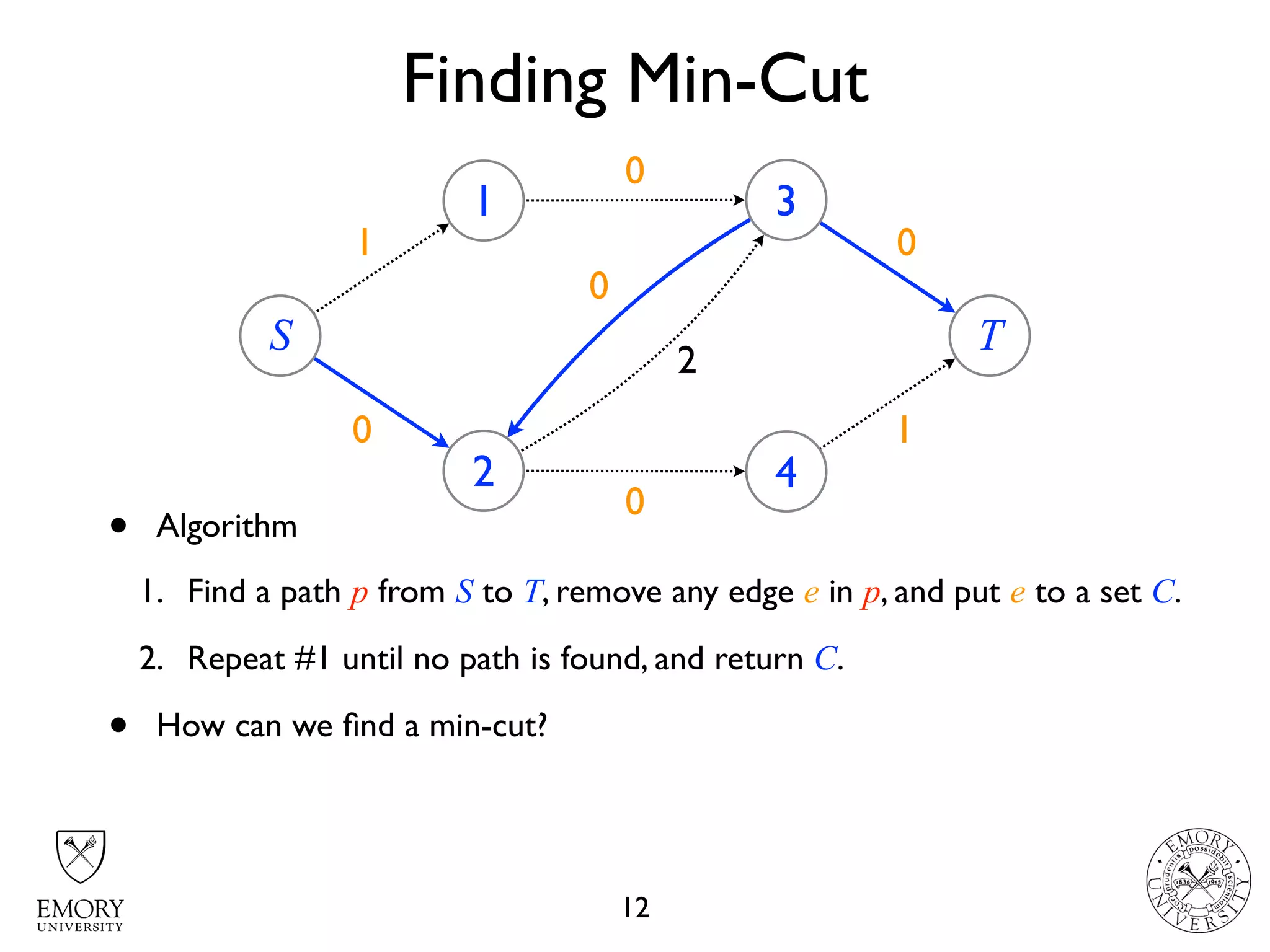
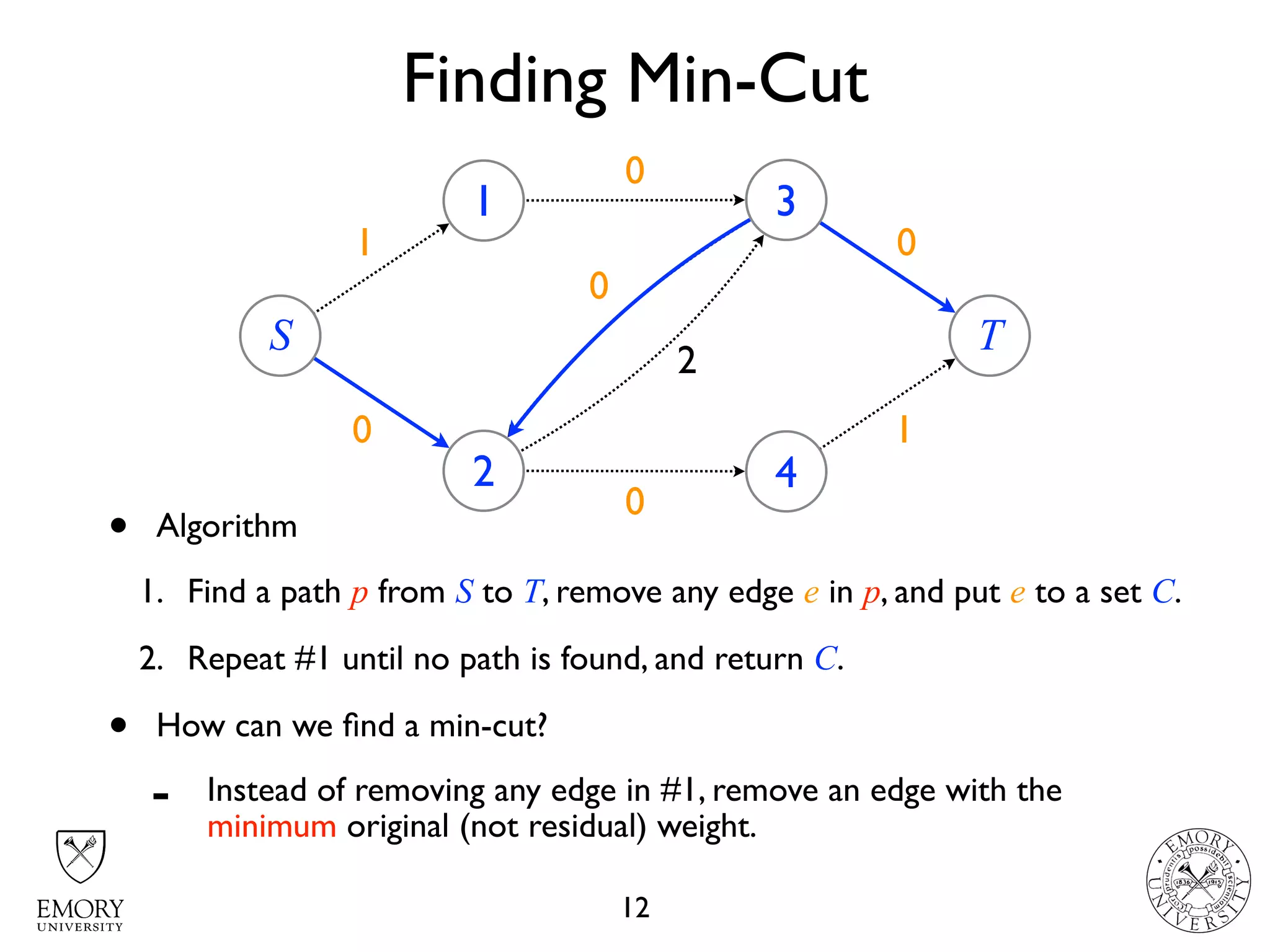
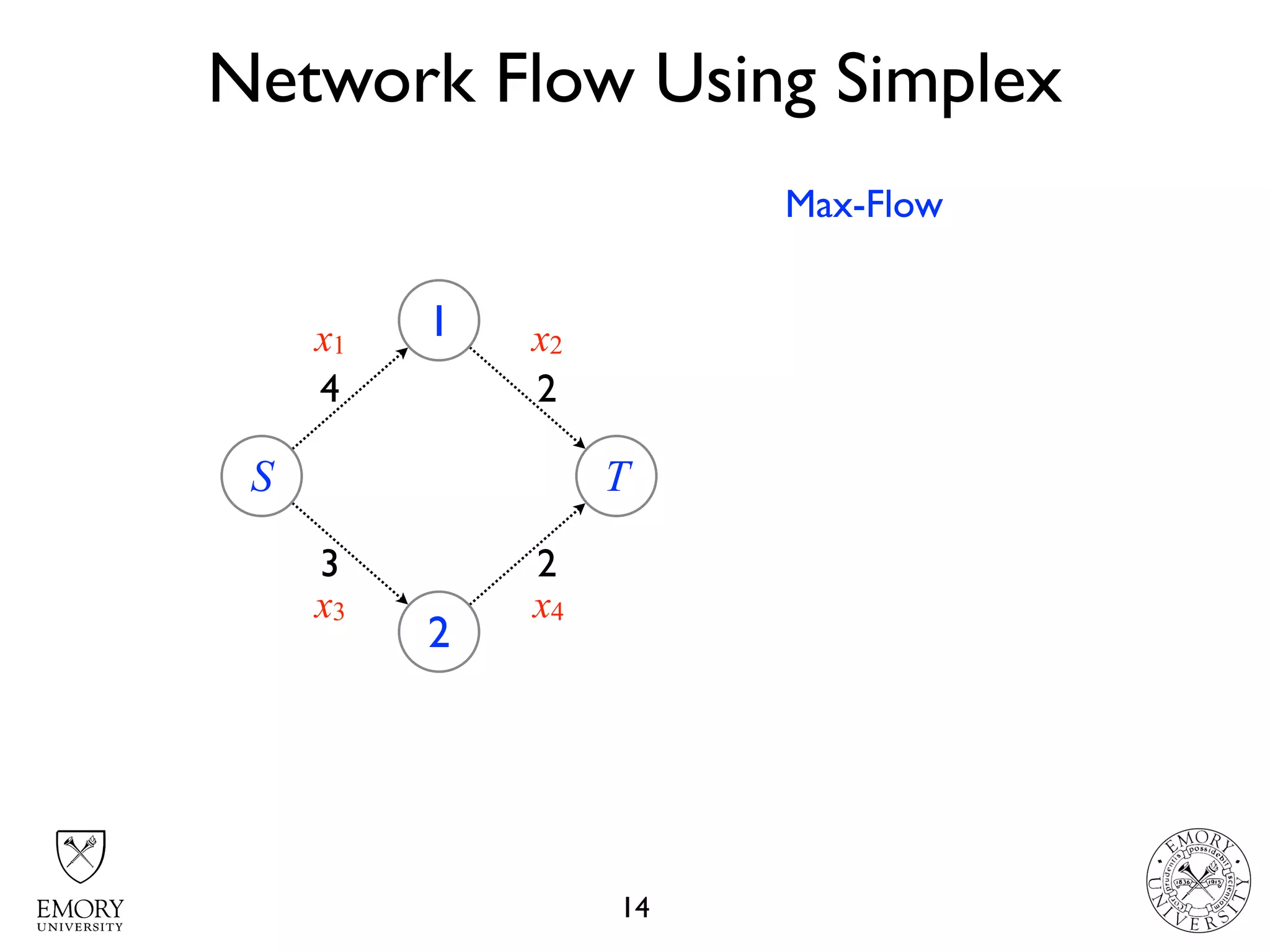
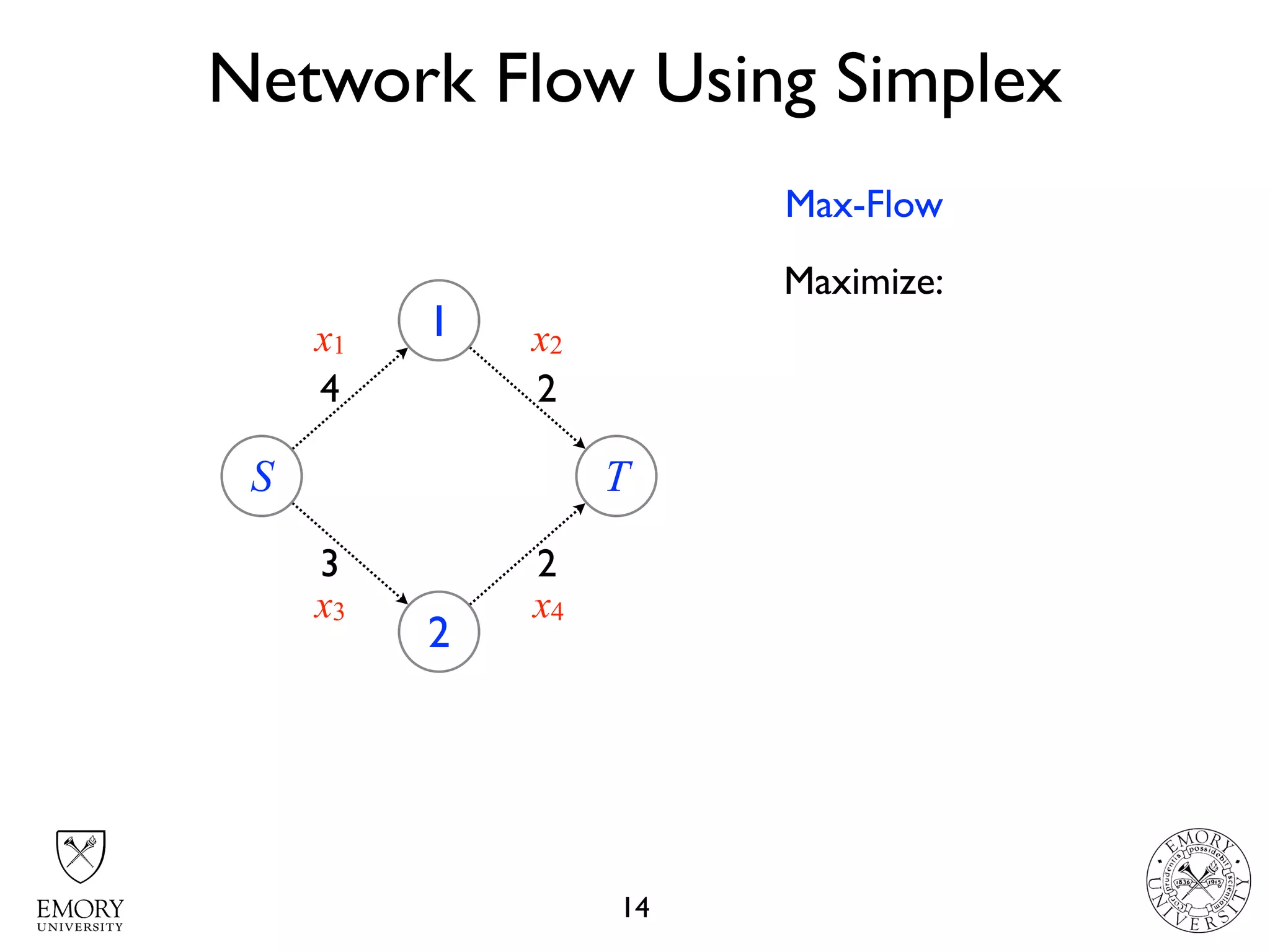
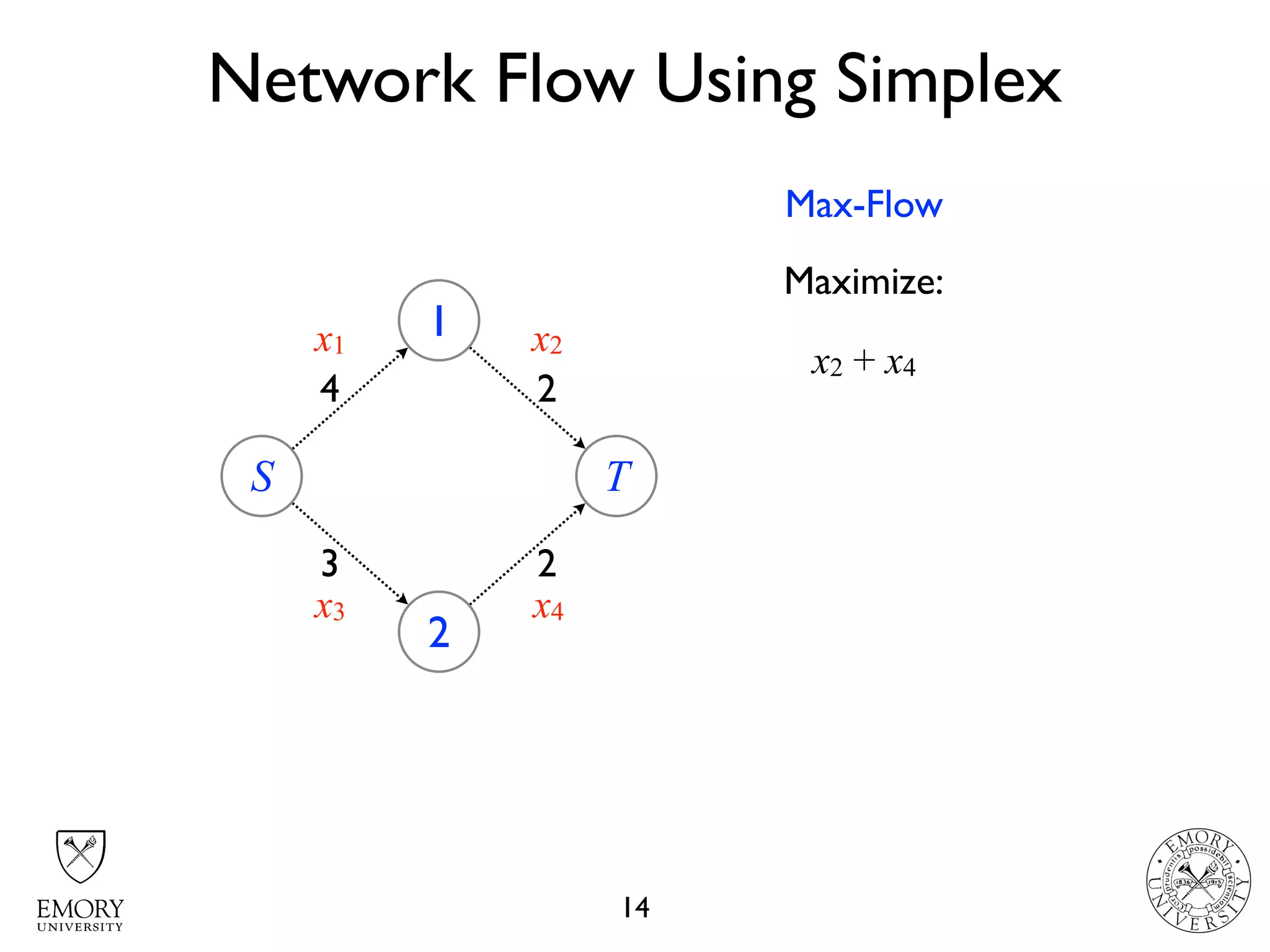
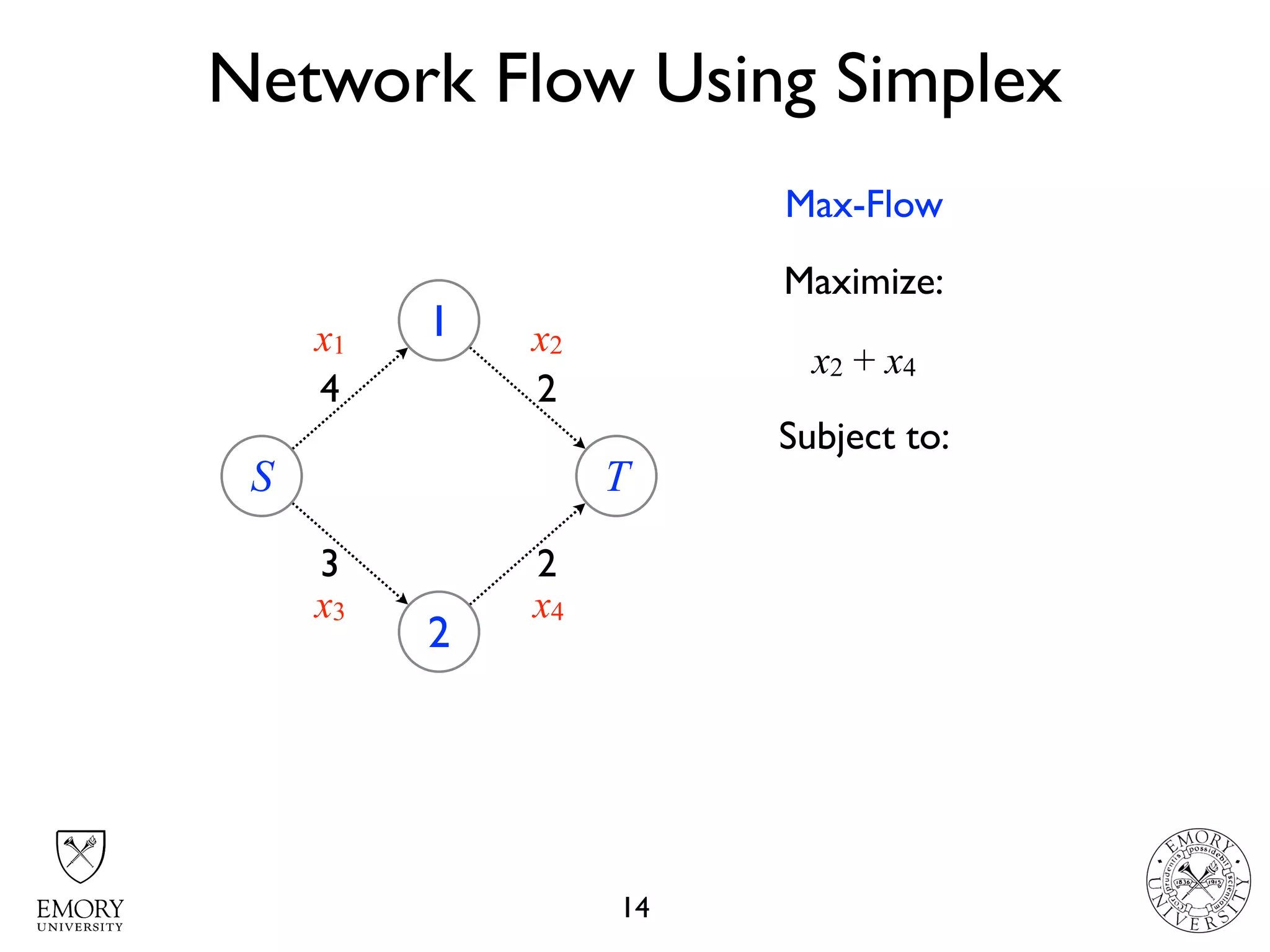
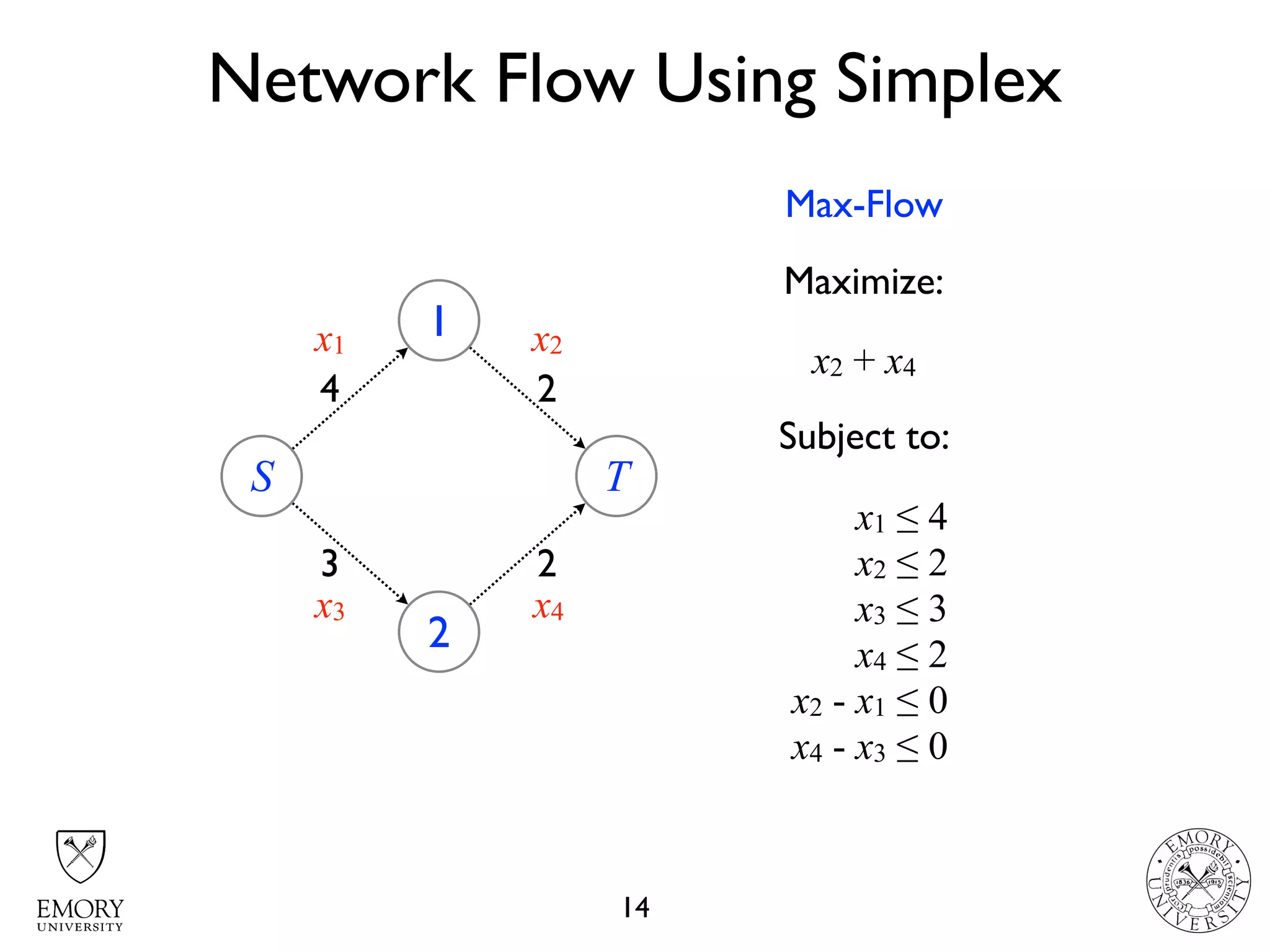
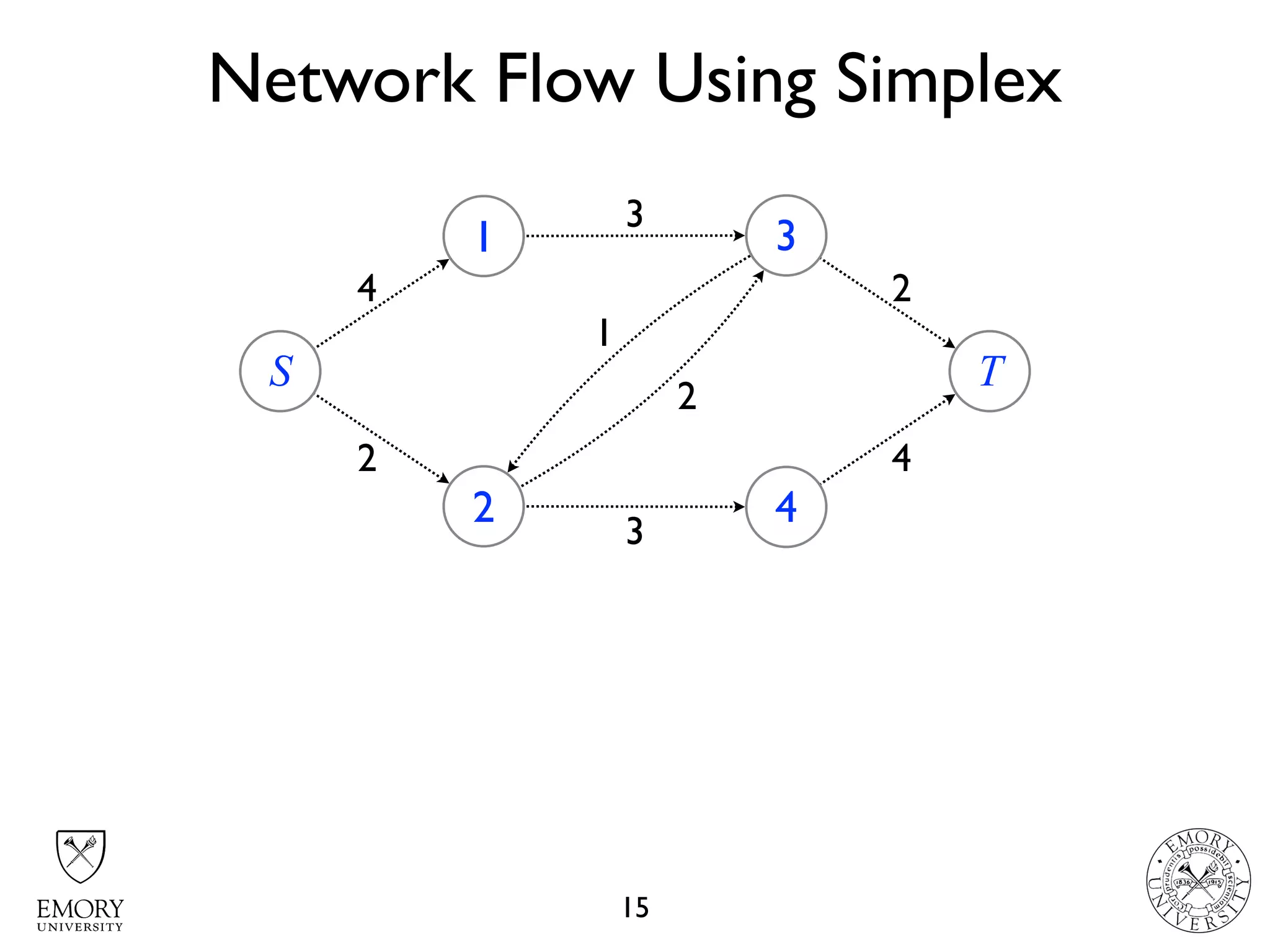
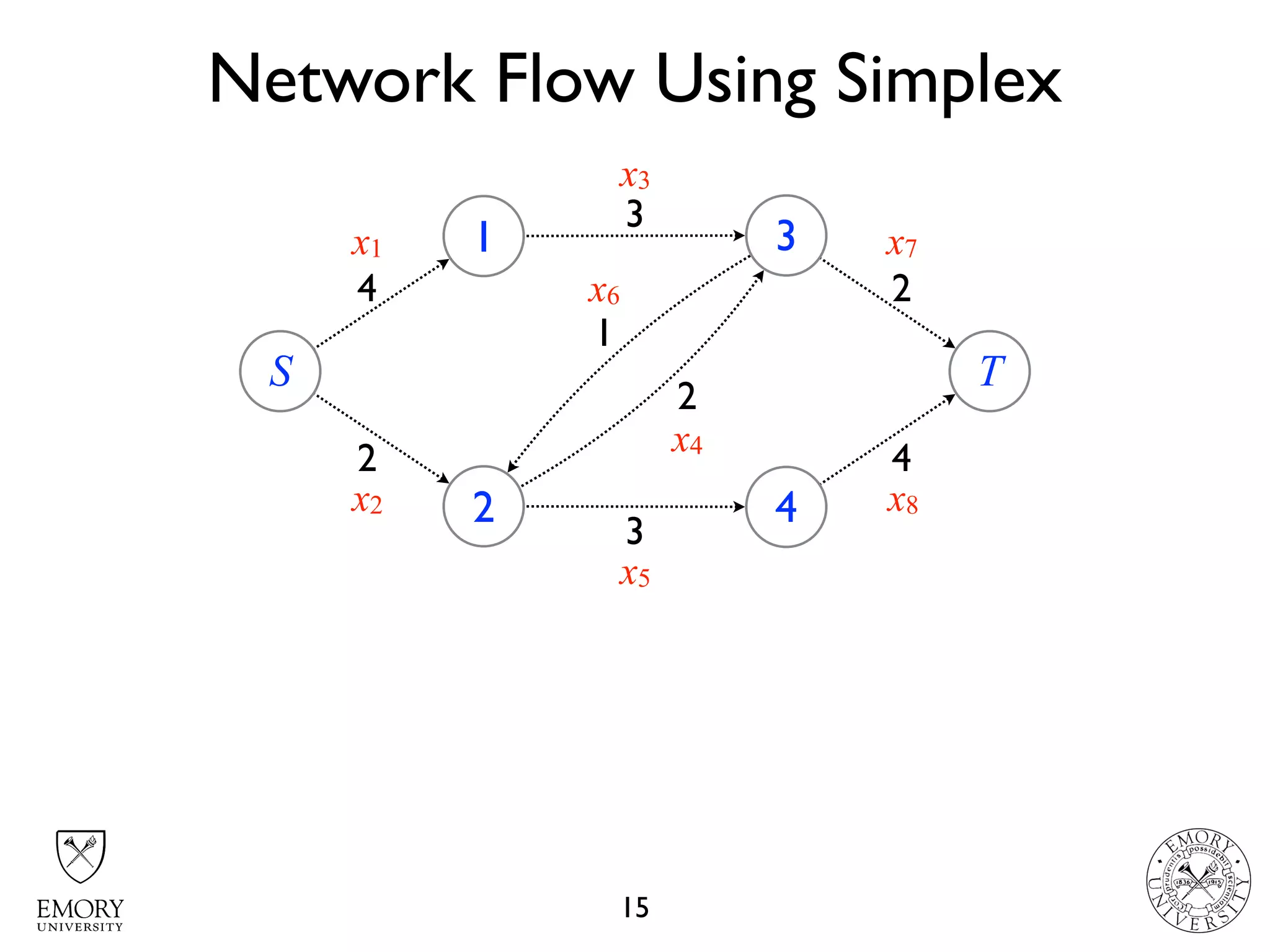
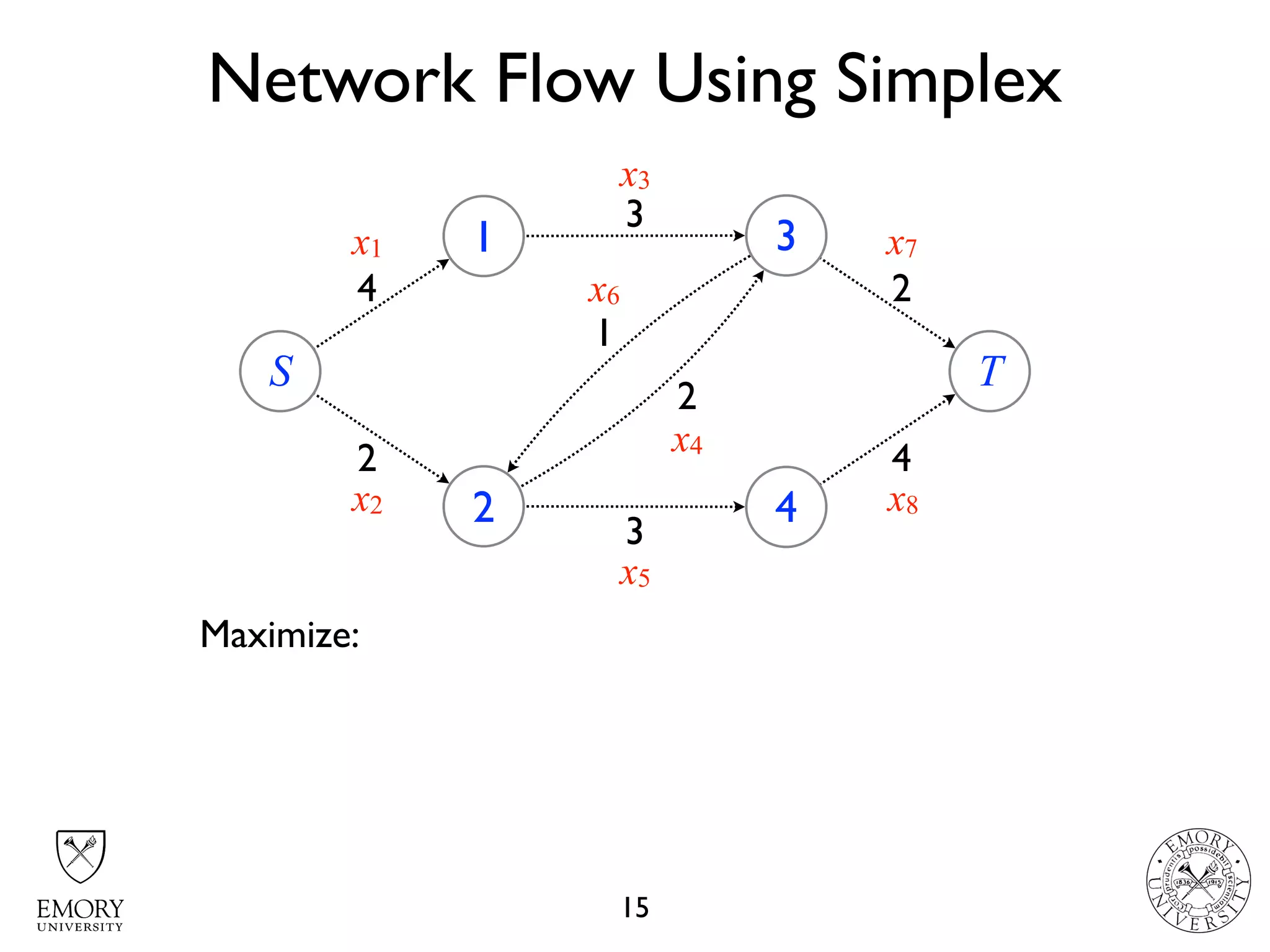
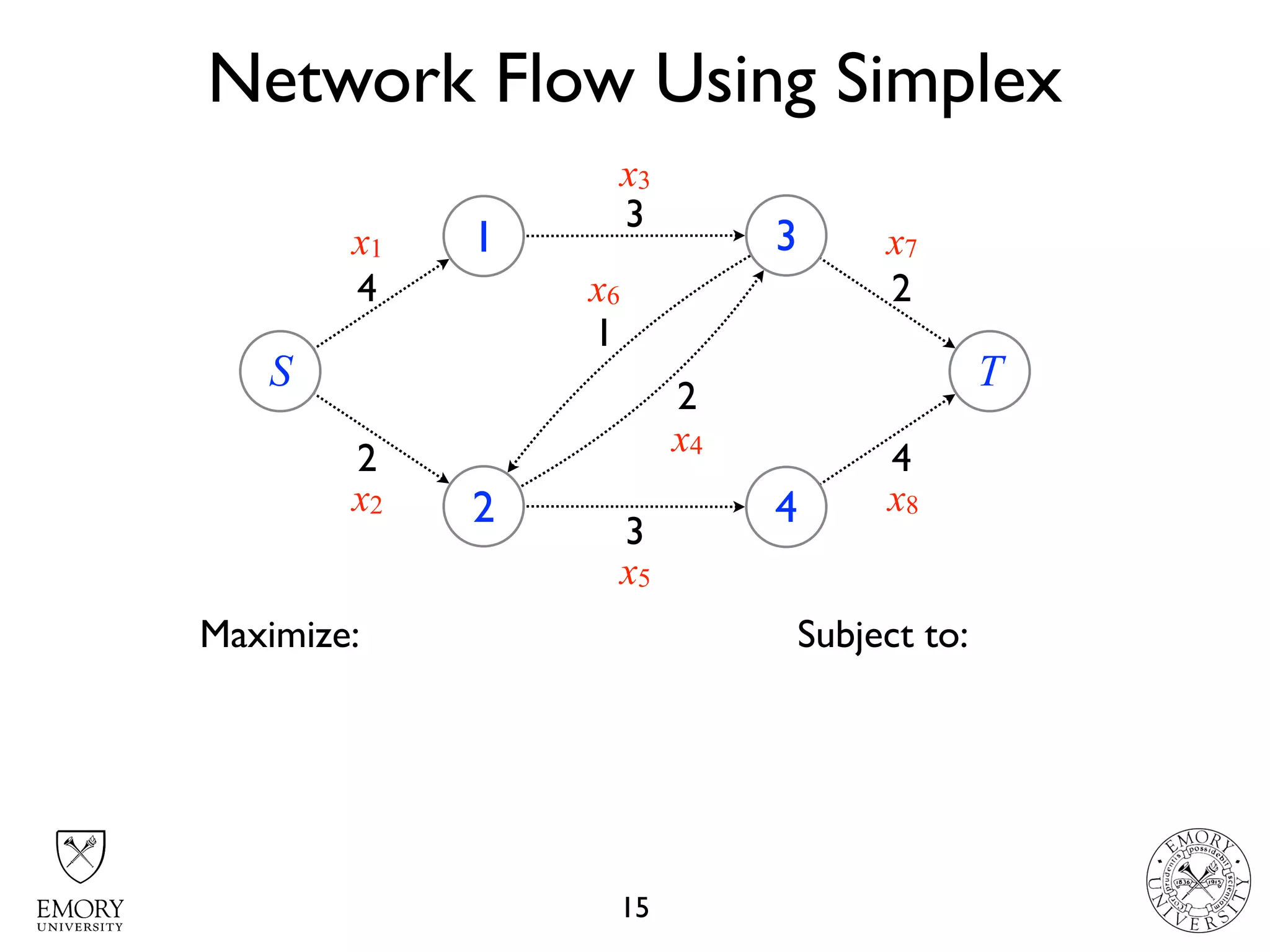
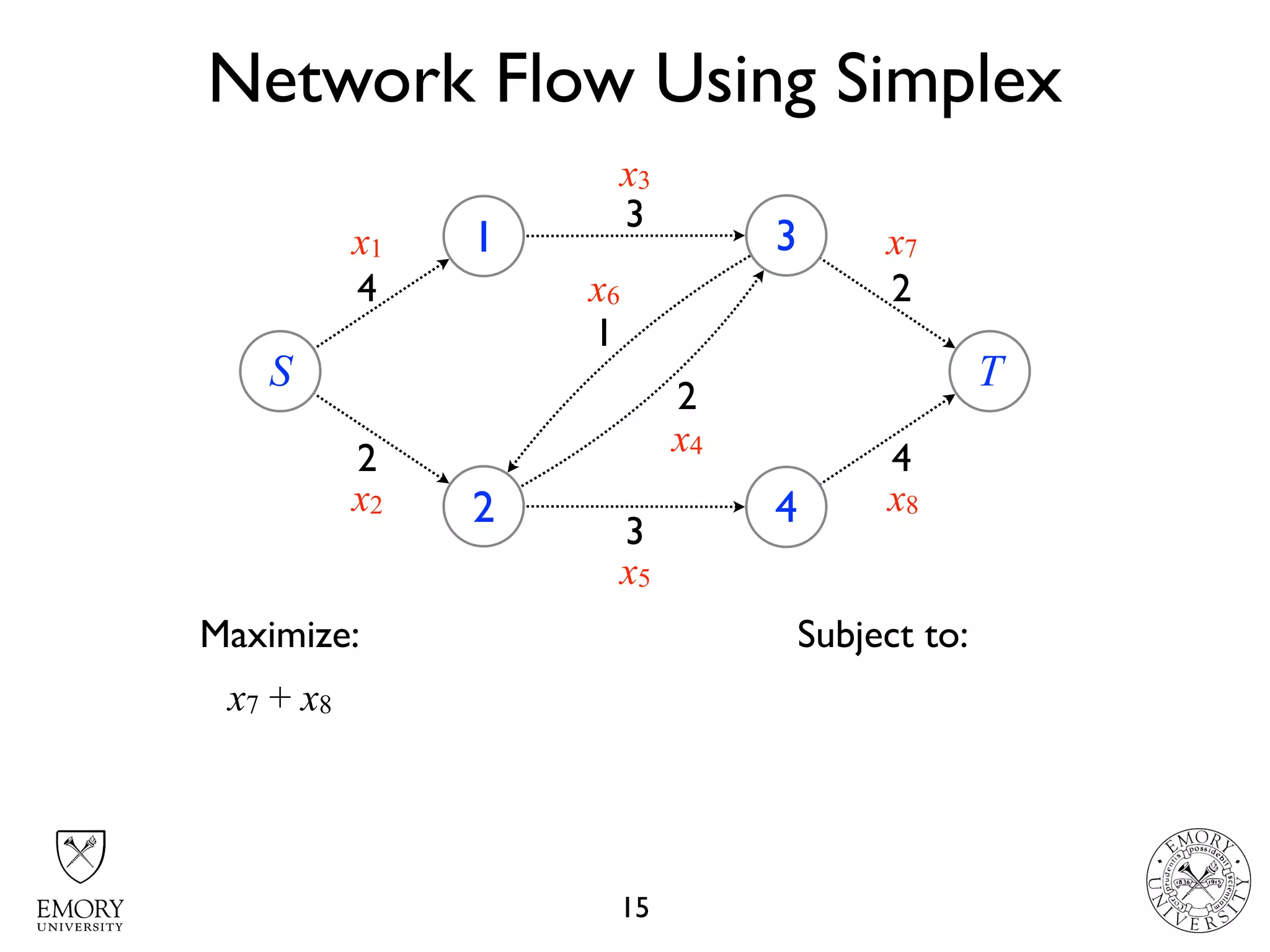
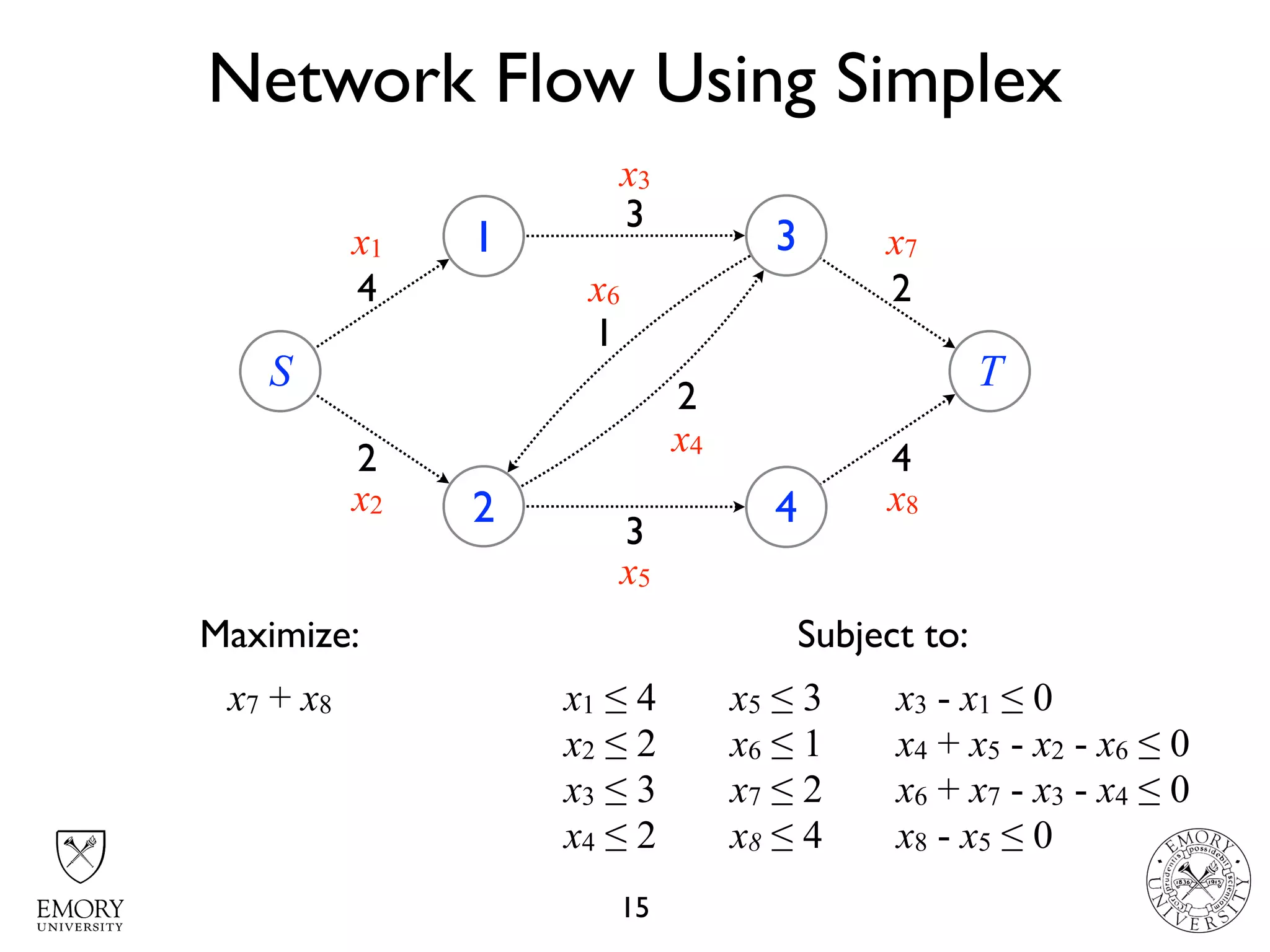
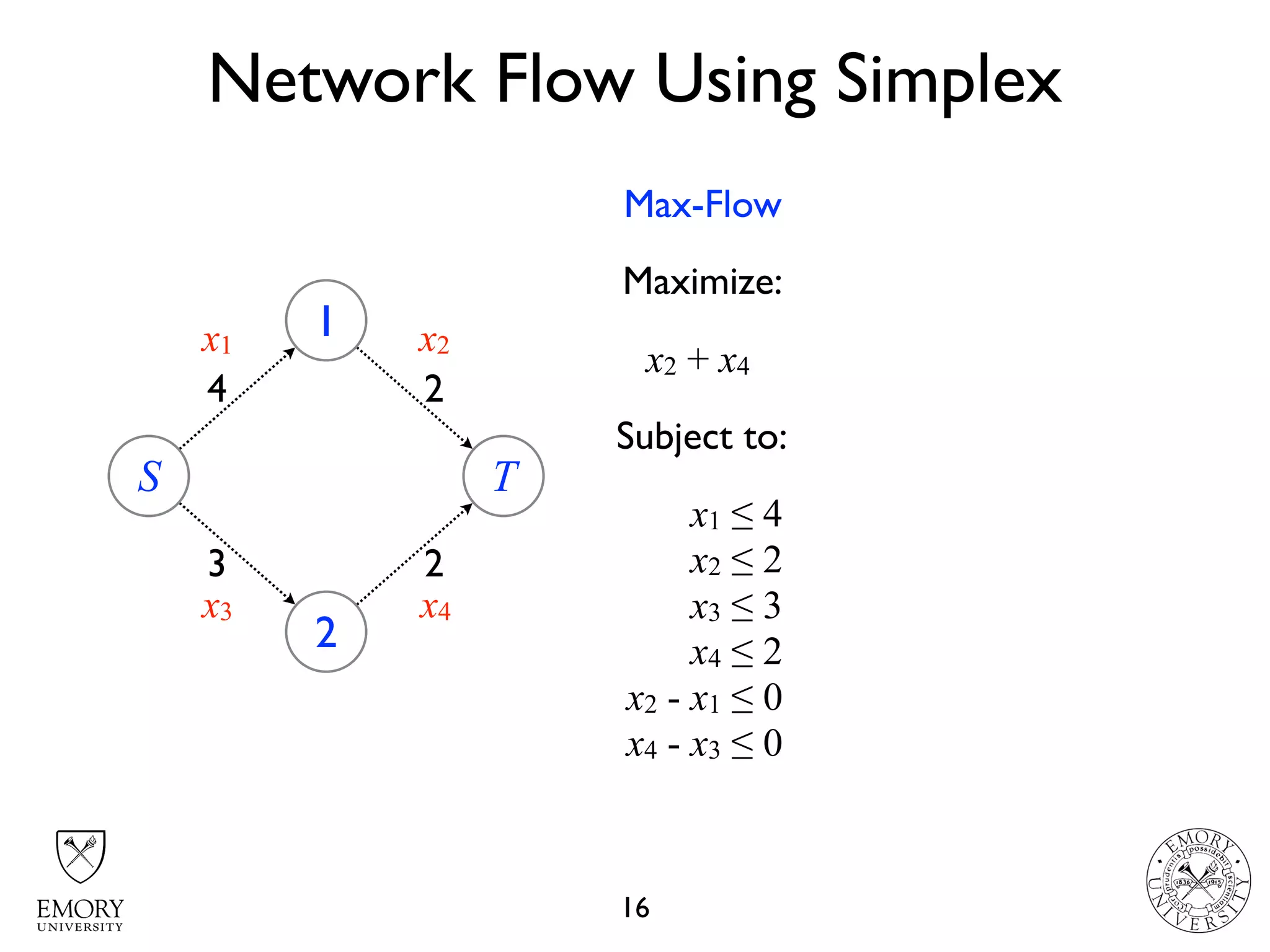
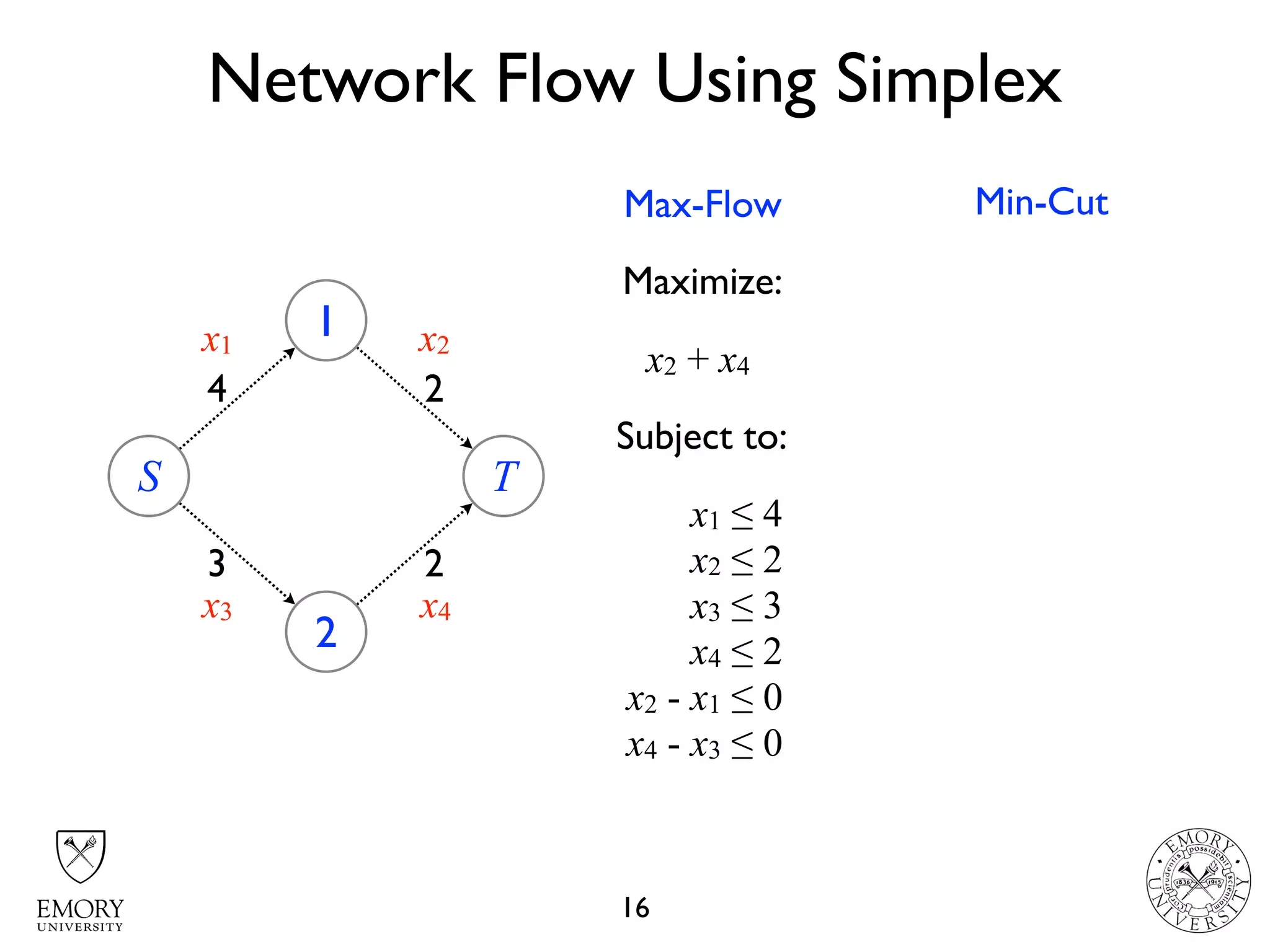
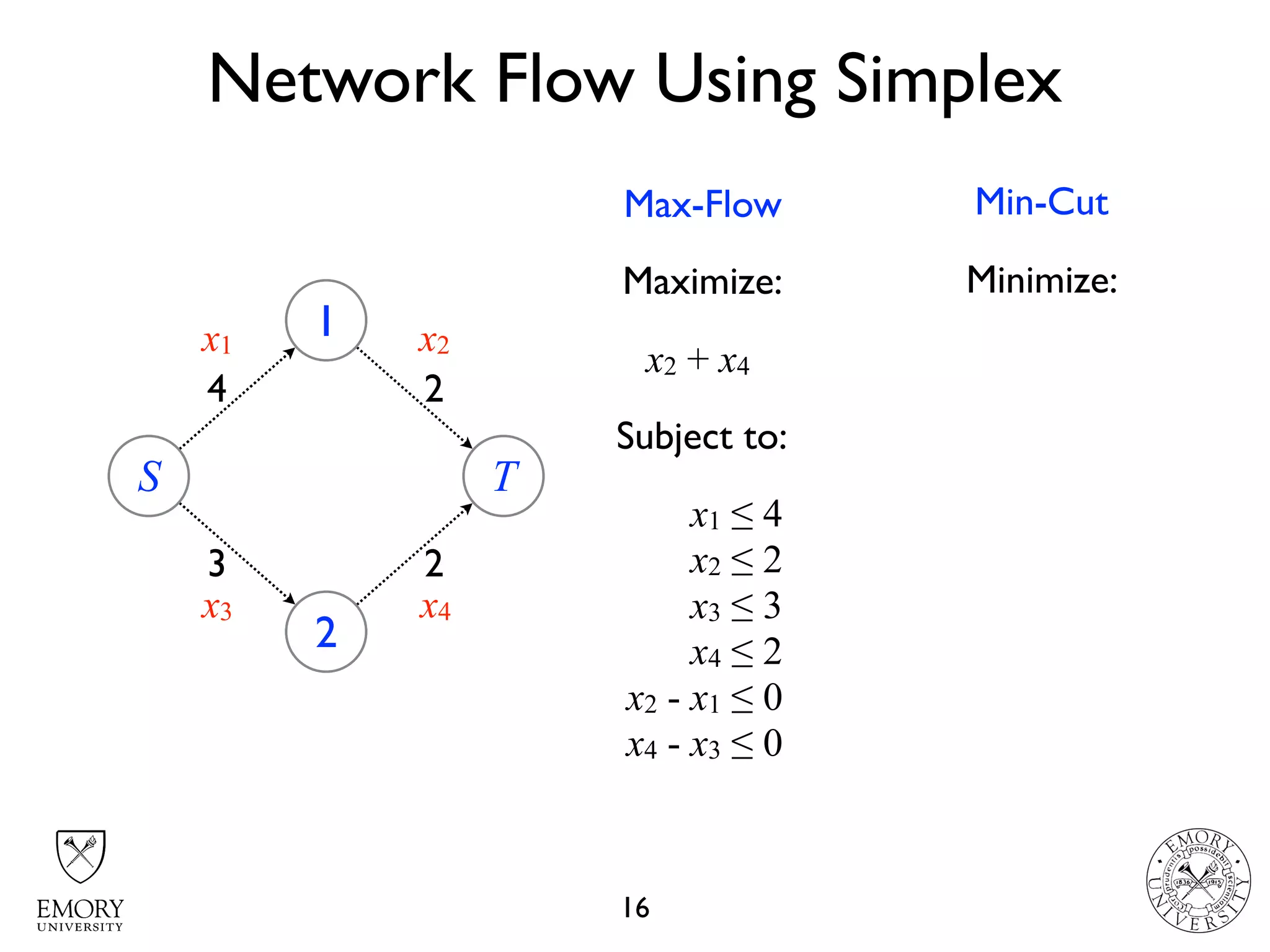
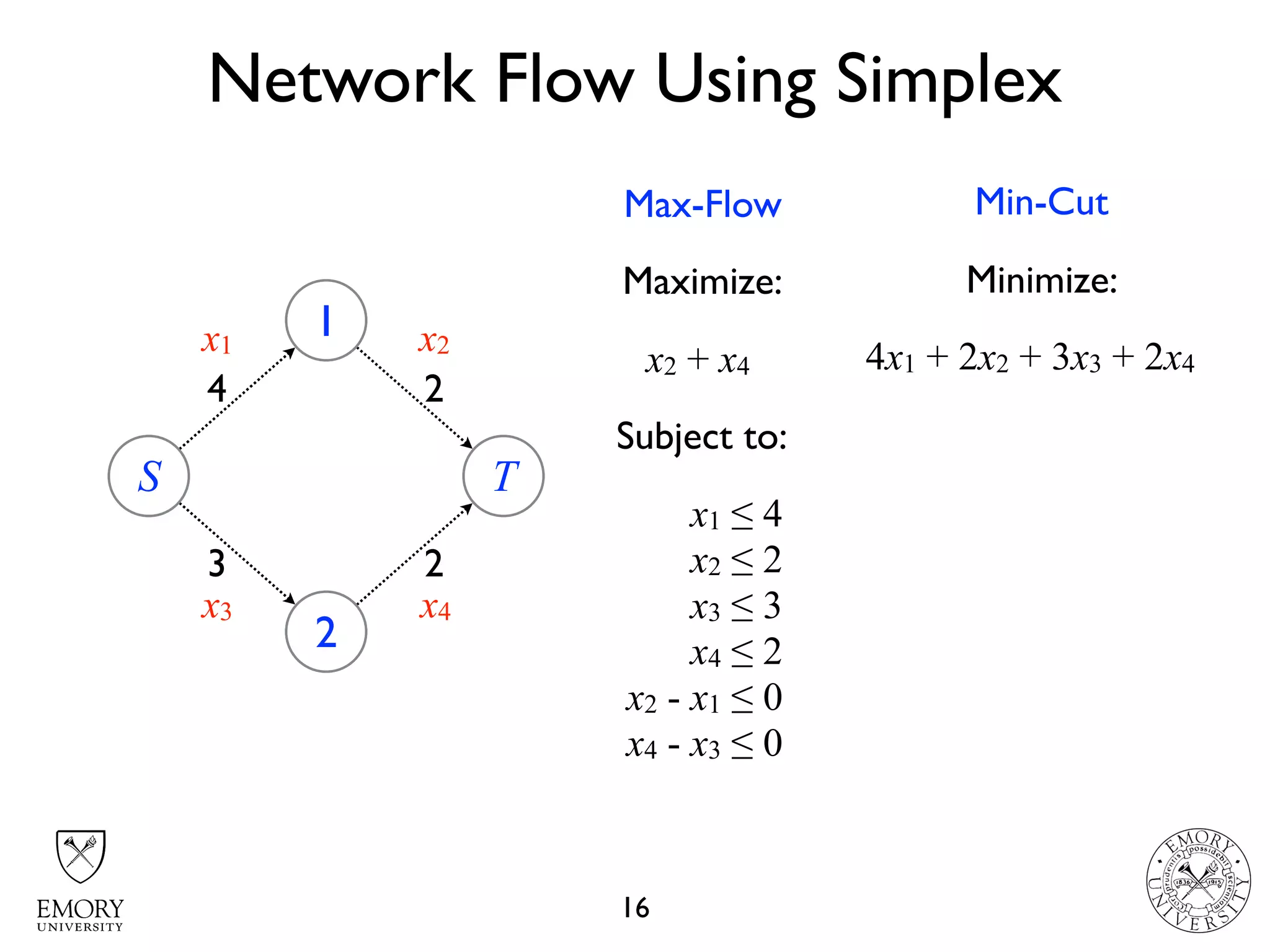
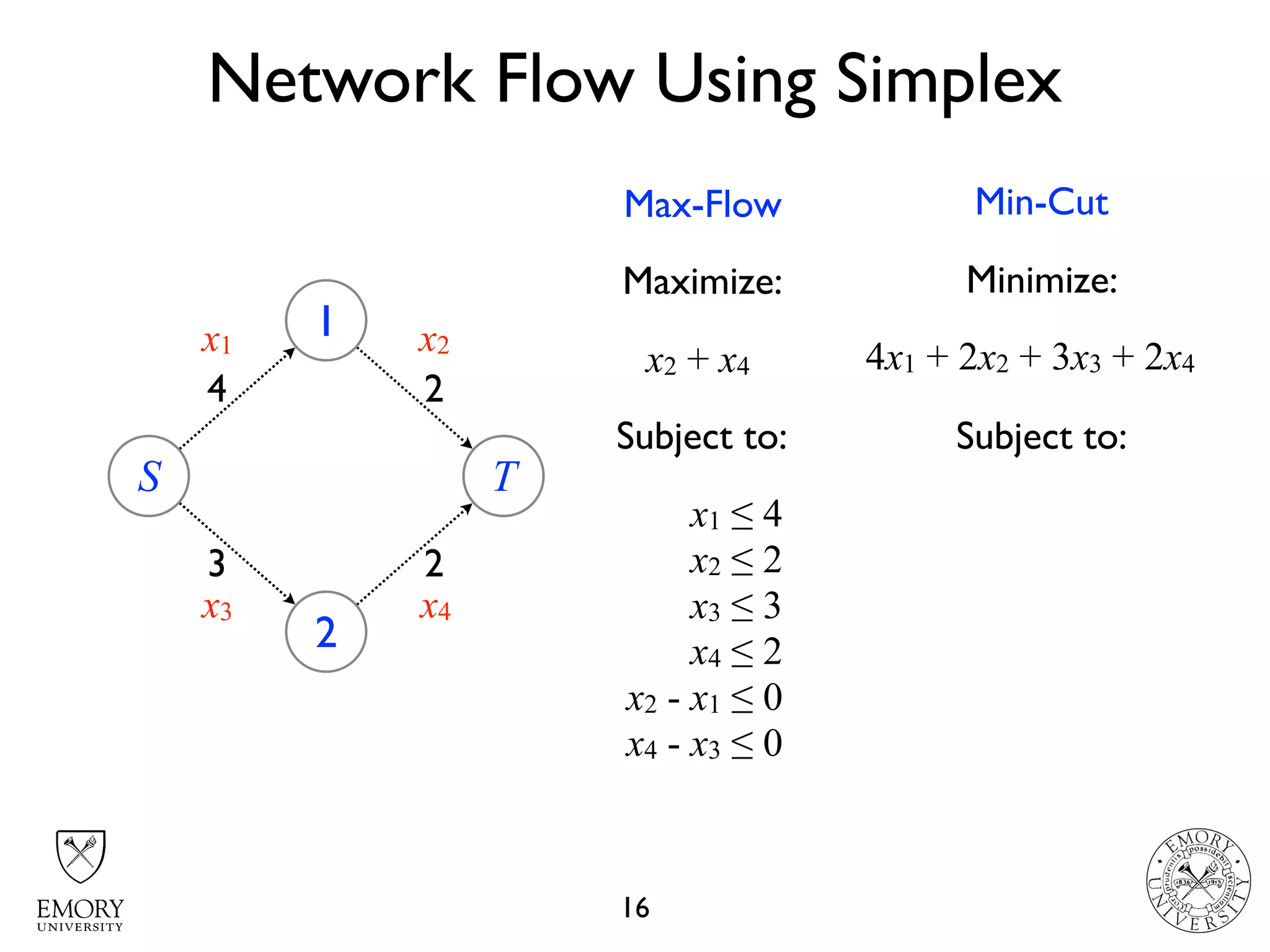
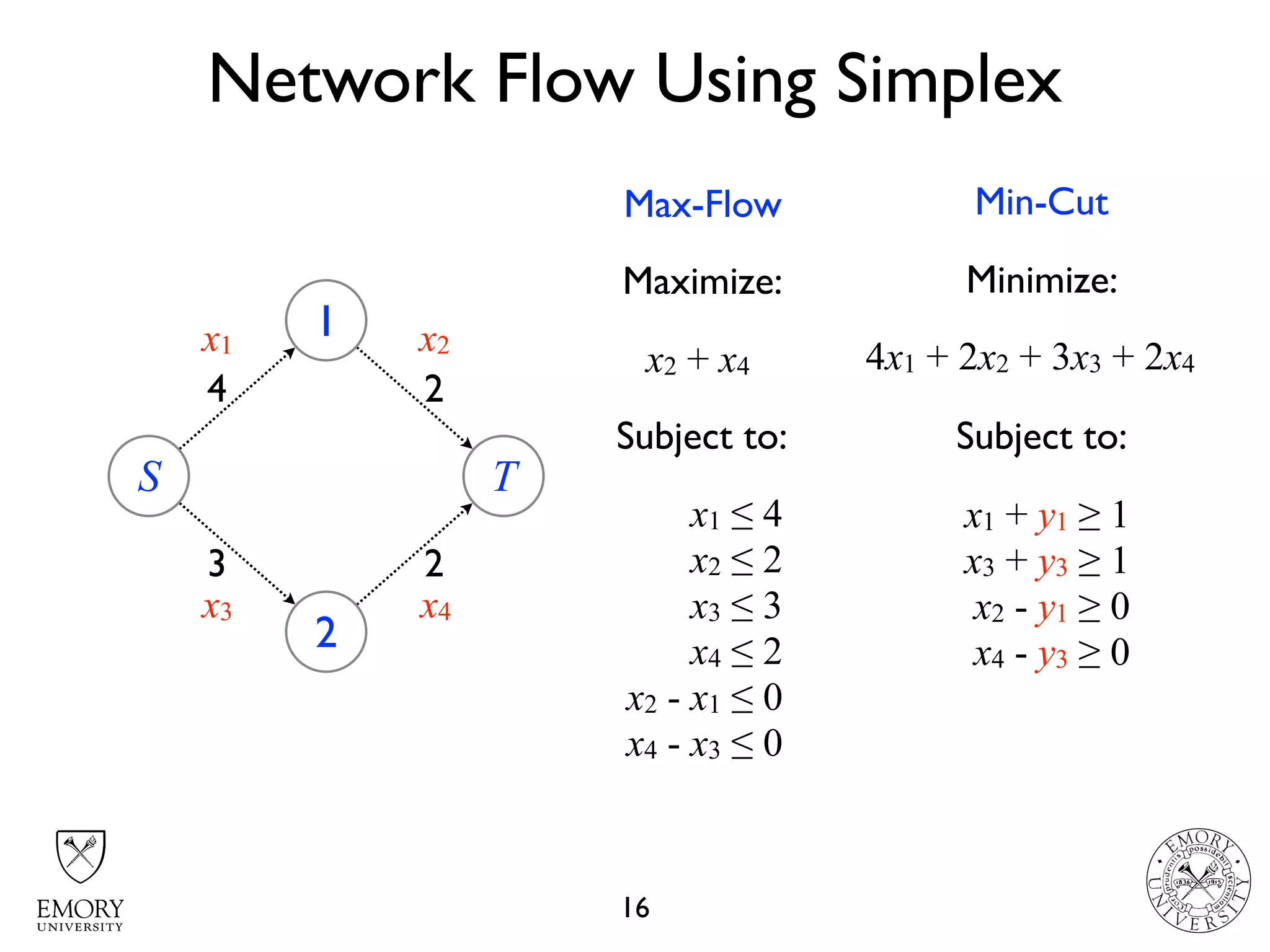
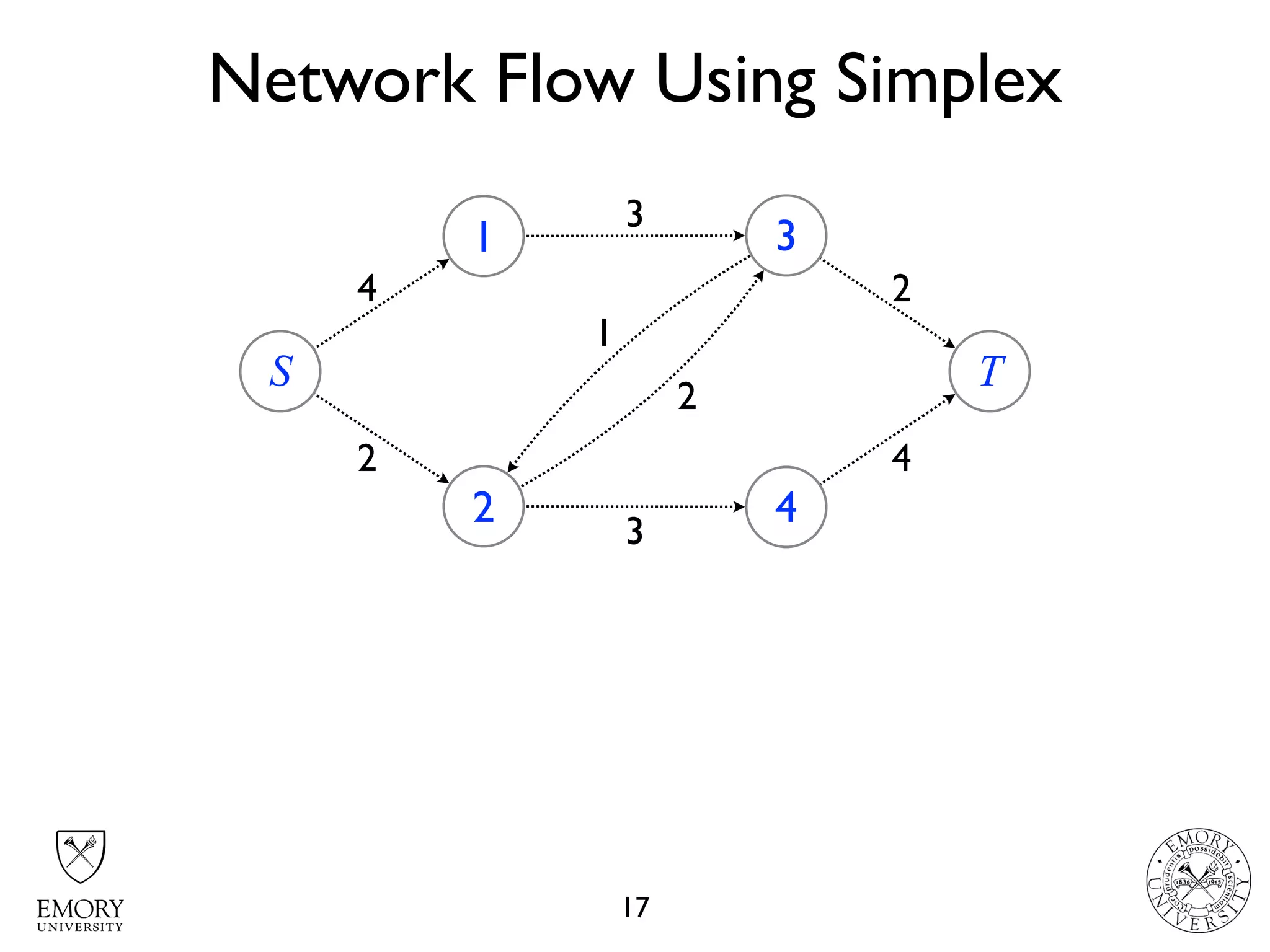
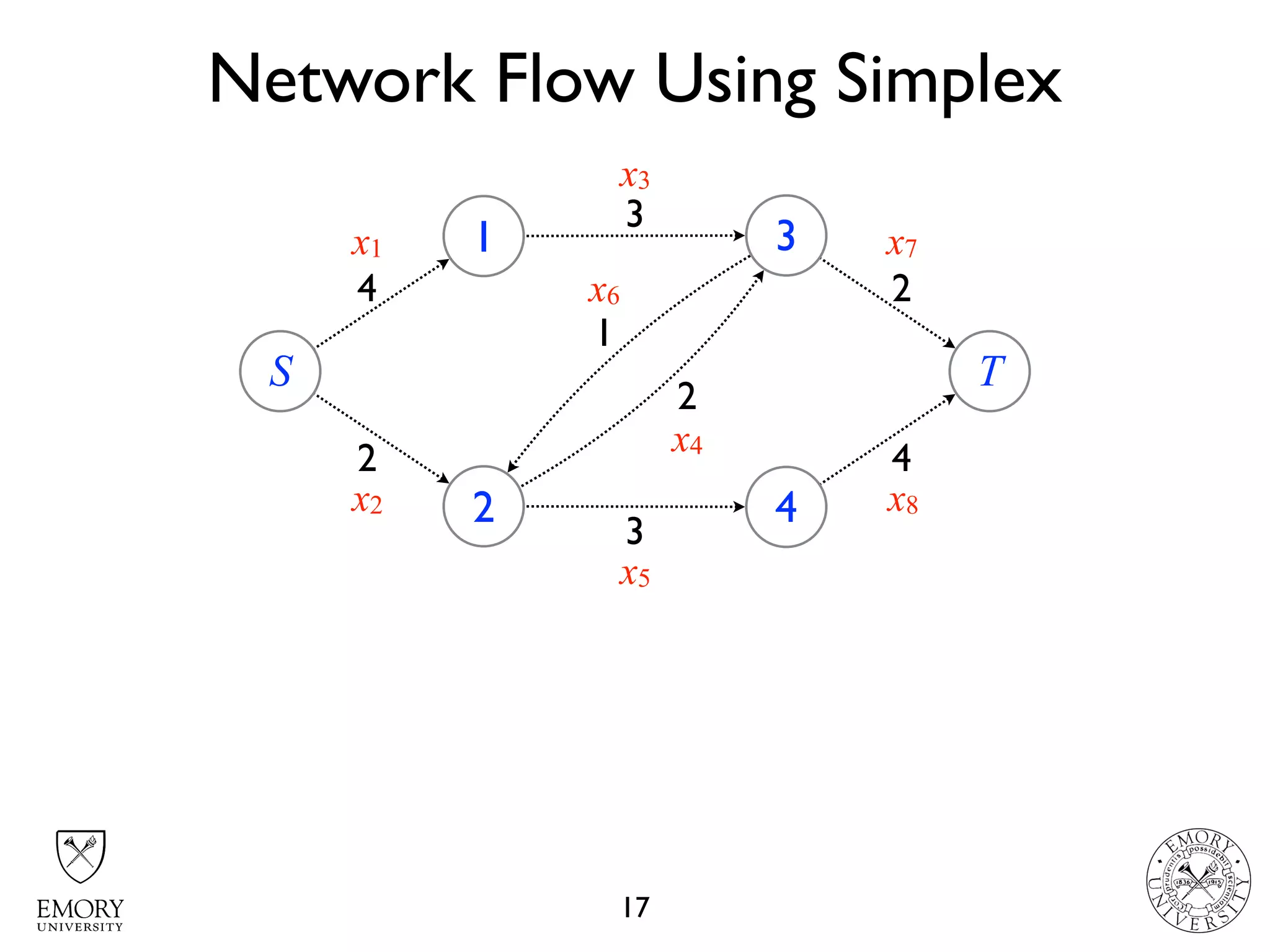
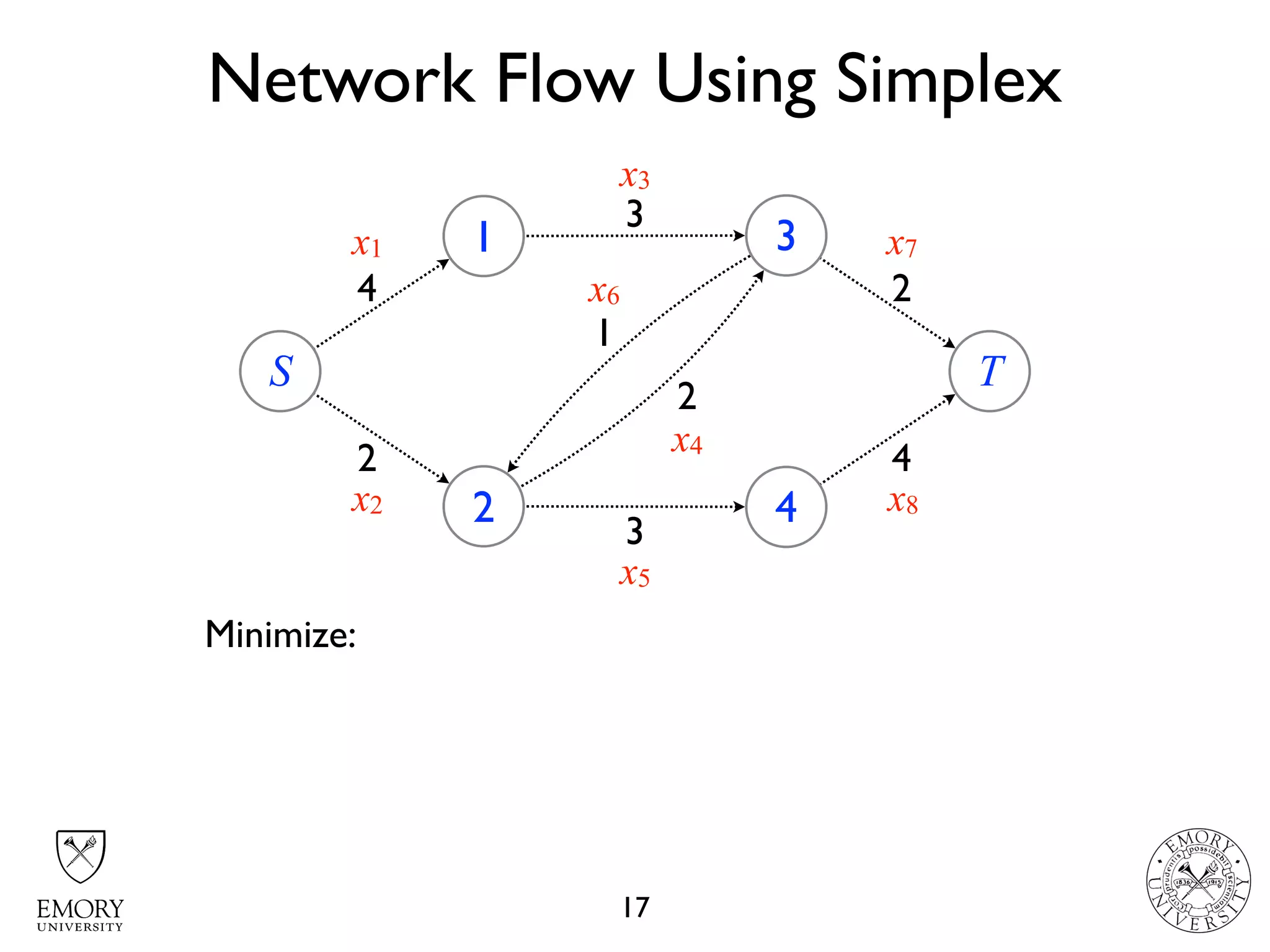
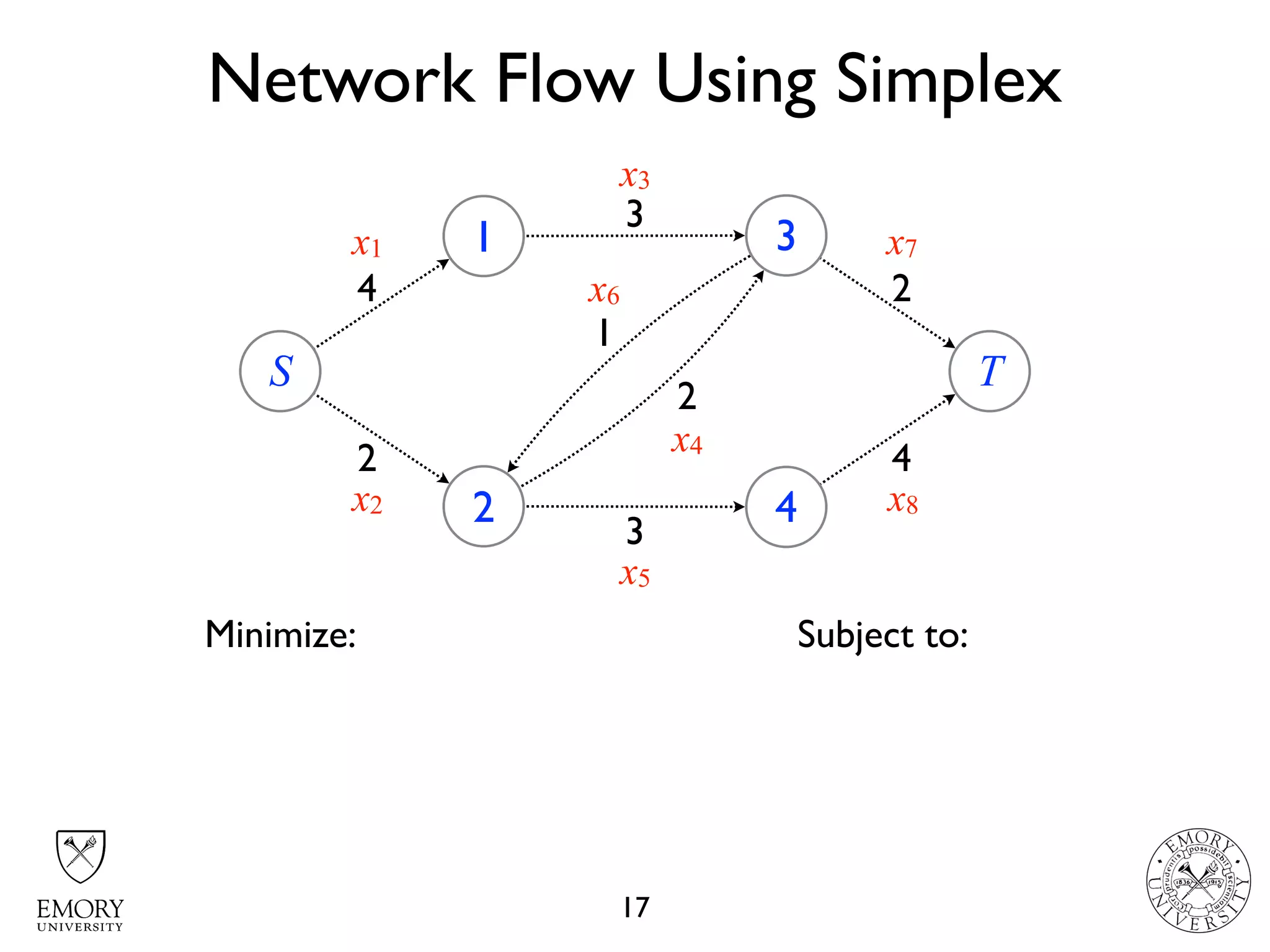
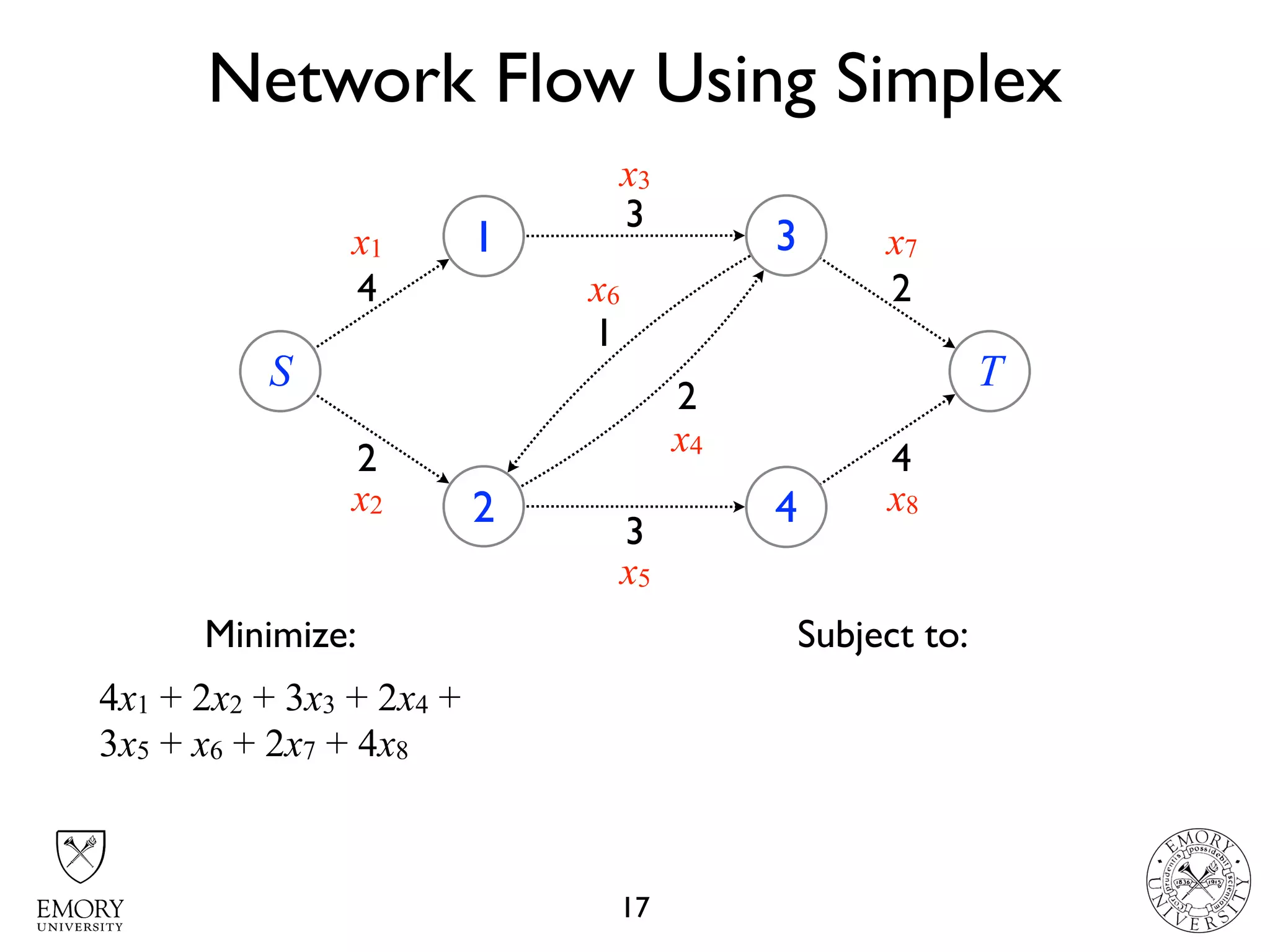
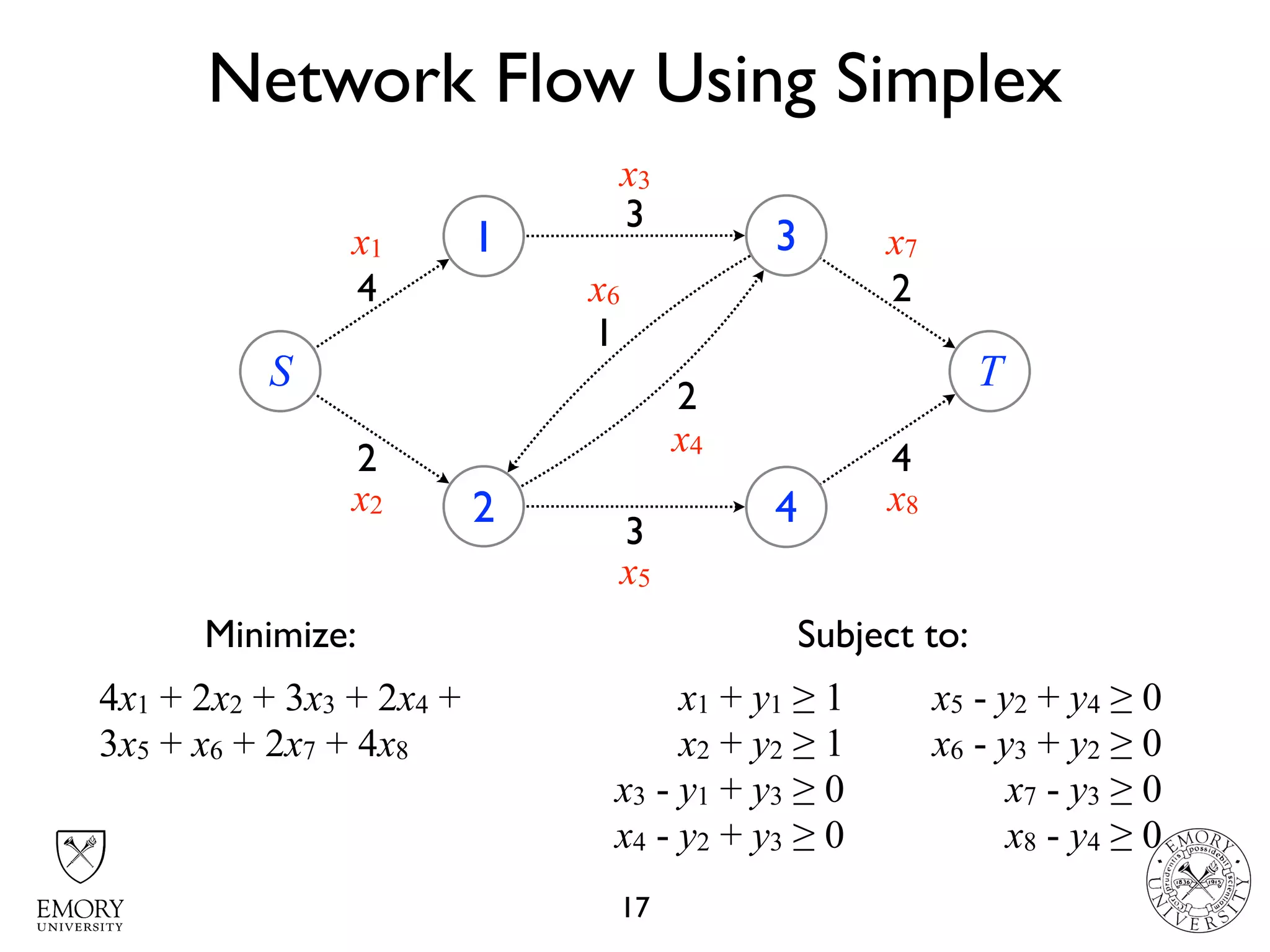
The document describes the maximum flow problem and Ford-Fulkerson algorithm for finding the maximum flow in a flow network. The maximum flow problem involves finding the maximum amount of flow that can be pushed from a source node S to a target node T in a flow network where each edge has a capacity. The Ford-Fulkerson algorithm iteratively finds augmenting paths (paths from S to T with available residual capacity) in the network and pushes flow along these paths until no more augmenting paths exist, giving the maximum flow. Pseudocode is provided for the MaxFlow and FordFulkerson classes that could implement this algorithm.

1. Network Flow
Data Structures and Algorithms
Emory University
Jinho D. Choi

2. Network Flow
2
S
1
2
3
4
T

3. Network Flow
2
S
1
2
3
4
T
Each edge e is associated with a capacity c.

4. Network Flow
2
S
1
2
3
4
T
4
2
3
1
2
3
4
2
Each edge e is associated with a capacity c.

5. Network Flow
2
S
1
2
3
4
T
4
2
3
1
2
3
4
2
Each edge e is associated with a capacity c.
Push as much flow f as possible from S to T.

6. Network Flow
2
S
1
2
3
4
T
4
2
3
1
2
3
4
2
Each edge e is associated with a capacity c.
Push as much flow f as possible from S to T.

7. Network Flow
2
S
1
2
3
4
T
4
2
3
1
2
3
4
2
Each edge e is associated with a capacity c.
Push as much flow f as possible from S to T.
f(e) ≤ c(e)

8. Network Flow
2
S
1
2
3
4
T
4
2
3
1
2
3
4
2
Each edge e is associated with a capacity c.
Push as much flow f as possible from S to T.
f(e) ≤ c(e)
Σu f(u, v) = Σw f(v, w), where v ∉ {S, T}

9. Network Flow
2
S
1
2
3
4
T
4
2
3
1
2
3
4
2
Each edge e is associated with a capacity c.
Push as much flow f as possible from S to T.
f(e) ≤ c(e)
Σu f(u, v) = Σw f(v, w), where v ∉ {S, T}
Maximum flow?

10. Network Flow
2
S
1
2
3
4
T
4
2
3
1
2
3
4
2
Each edge e is associated with a capacity c.
Push as much flow f as possible from S to T.
f(e) ≤ c(e)
Σu f(u, v) = Σw f(v, w), where v ∉ {S, T}
3
Maximum flow?

11. Network Flow
2
S
1
2
3
4
T
4
2
3
1
2
3
4
2
Each edge e is associated with a capacity c.
Push as much flow f as possible from S to T.
f(e) ≤ c(e)
Σu f(u, v) = Σw f(v, w), where v ∉ {S, T}
3
3
Maximum flow?

12. Network Flow
2
S
1
2
3
4
T
4
2
3
1
2
3
4
2
Each edge e is associated with a capacity c.
Push as much flow f as possible from S to T.
f(e) ≤ c(e)
Σu f(u, v) = Σw f(v, w), where v ∉ {S, T}
3
3
1
2
Maximum flow?

13. Network Flow
2
S
1
2
3
4
T
4
2
3
1
2
3
4
2
Each edge e is associated with a capacity c.
Push as much flow f as possible from S to T.
f(e) ≤ c(e)
Σu f(u, v) = Σw f(v, w), where v ∉ {S, T}
3
3
1
2
2
Maximum flow?

14. Network Flow
2
S
1
2
3
4
T
4
2
3
1
2
3
4
2
Each edge e is associated with a capacity c.
Push as much flow f as possible from S to T.
f(e) ≤ c(e)
Σu f(u, v) = Σw f(v, w), where v ∉ {S, T}
3
3
1
2
2
1+2
Maximum flow?

15. Network Flow
2
S
1
2
3
4
T
4
2
3
1
2
3
4
2
Each edge e is associated with a capacity c.
Push as much flow f as possible from S to T.
f(e) ≤ c(e)
Σu f(u, v) = Σw f(v, w), where v ∉ {S, T}
3
3
1
2
2
1+2
3
Maximum flow?

16. Network Flow
2
S
1
2
3
4
T
4
2
3
1
2
3
4
2
Each edge e is associated with a capacity c.
Push as much flow f as possible from S to T.
f(e) ≤ c(e)
Σu f(u, v) = Σw f(v, w), where v ∉ {S, T}
3
3
1
2
2
1+2
3
Maximum flow? Optimum?

17. 4
4 2
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3

18. 4
4 2
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3
Find a path p from S to T, where ∀e 𝜖 p. r(e) = c(e) - f(e) > 0.

19. 4
4 2
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3
Find a path p from S to T, where ∀e 𝜖 p. r(e) = c(e) - f(e) > 0.

20. 4
4 2
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3
Find a path p from S to T, where ∀e 𝜖 p. r(e) = c(e) - f(e) > 0.
∀e 𝜖 p. c(e) = c(e) - min(f(p)).

21. 4
4 2
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3
Find a path p from S to T, where ∀e 𝜖 p. r(e) = c(e) - f(e) > 0.
∀e 𝜖 p. c(e) = c(e) - min(f(p)).

22. 4
4 22 0
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3
1
Find a path p from S to T, where ∀e 𝜖 p. r(e) = c(e) - f(e) > 0.
∀e 𝜖 p. c(e) = c(e) - min(f(p)).

23. 4
4 22 0
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3
1
Find a path p from S to T, where ∀e 𝜖 p. r(e) = c(e) - f(e) > 0.
∀e 𝜖 p. c(e) = c(e) - min(f(p)).
MaxFlow = MaxFlow + min(f(p)).

24. 4
4 22 0
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3
1
Find a path p from S to T, where ∀e 𝜖 p. r(e) = c(e) - f(e) > 0.
∀e 𝜖 p. c(e) = c(e) - min(f(p)).
MaxFlow = MaxFlow + min(f(p)).
2

25. 4
4 22 0
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3
1
Find a path p from S to T, where ∀e 𝜖 p. r(e) = c(e) - f(e) > 0.
∀e 𝜖 p. c(e) = c(e) - min(f(p)).
MaxFlow = MaxFlow + min(f(p)).
2

26. 4
4 22 0
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3
1
Find a path p from S to T, where ∀e 𝜖 p. r(e) = c(e) - f(e) > 0.
∀e 𝜖 p. c(e) = c(e) - min(f(p)).
MaxFlow = MaxFlow + min(f(p)).
2

27. 4
4 22 0
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3
1
Find a path p from S to T, where ∀e 𝜖 p. r(e) = c(e) - f(e) > 0.
∀e 𝜖 p. c(e) = c(e) - min(f(p)).
MaxFlow = MaxFlow + min(f(p)).
2

28. 43
4 22 01
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3
1
Find a path p from S to T, where ∀e 𝜖 p. r(e) = c(e) - f(e) > 0.
∀e 𝜖 p. c(e) = c(e) - min(f(p)).
MaxFlow = MaxFlow + min(f(p)).
2
0
0
2

29. 43
4 22 01
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3
1
Find a path p from S to T, where ∀e 𝜖 p. r(e) = c(e) - f(e) > 0.
∀e 𝜖 p. c(e) = c(e) - min(f(p)).
MaxFlow = MaxFlow + min(f(p)).
2
0
0
2
1

30. 43
4 22 01
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3
1
Find a path p from S to T, where ∀e 𝜖 p. r(e) = c(e) - f(e) > 0.
∀e 𝜖 p. c(e) = c(e) - min(f(p)).
MaxFlow = MaxFlow + min(f(p)).
2
0
0
2
1

31. 43
4 22 01
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3
1
Find a path p from S to T, where ∀e 𝜖 p. r(e) = c(e) - f(e) > 0.
∀e 𝜖 p. c(e) = c(e) - min(f(p)).
MaxFlow = MaxFlow + min(f(p)).
2
0
0
2
1

32. 43
4 22 01
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3
1
Find a path p from S to T, where ∀e 𝜖 p. r(e) = c(e) - f(e) > 0.
∀e 𝜖 p. c(e) = c(e) - min(f(p)).
MaxFlow = MaxFlow + min(f(p)).
2
0
0
2
1

33. 431
4 22 01
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3
1
Find a path p from S to T, where ∀e 𝜖 p. r(e) = c(e) - f(e) > 0.
∀e 𝜖 p. c(e) = c(e) - min(f(p)).
MaxFlow = MaxFlow + min(f(p)).
2
0
0
2
1
0
0

34. 431
4 22 01
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3
1
Find a path p from S to T, where ∀e 𝜖 p. r(e) = c(e) - f(e) > 0.
∀e 𝜖 p. c(e) = c(e) - min(f(p)).
MaxFlow = MaxFlow + min(f(p)).
2
0
0
2
1
0
0
2

35. 431
4 22 01
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3
1
Find a path p from S to T, where ∀e 𝜖 p. r(e) = c(e) - f(e) > 0.
∀e 𝜖 p. c(e) = c(e) - min(f(p)).
MaxFlow = MaxFlow + min(f(p)).
2
0
0
2
1
0
0
2

36. 431
4 22 01
Ford-Fulkerson Algorithm
3
S
1
2
3
4
T
2
3
1
2
3
1
Find a path p from S to T, where ∀e 𝜖 p. r(e) = c(e) - f(e) > 0.
∀e 𝜖 p. c(e) = c(e) - min(f(p)).
MaxFlow = MaxFlow + min(f(p)).
2
0
0
2
1
0
0
2
No more
augmenting path!

37. MaxFlow Class
4
public class MaxFlow
{
private Map<Edge,Double> m_flows;
private double d_maxFlow;
public MaxFlow(Graph graph)
{
init(graph);
}
public void init(Graph graph)
{
m_flows = new HashMap<>();
d_maxFlow = 0;
for (Edge edge : graph.getAllEdges())
m_flows.put(edge, 0d);
}
}

38. MaxFlow Class
4
public class MaxFlow
{
private Map<Edge,Double> m_flows;
private double d_maxFlow;
public MaxFlow(Graph graph)
{
init(graph);
}
public void init(Graph graph)
{
m_flows = new HashMap<>();
d_maxFlow = 0;
for (Edge edge : graph.getAllEdges())
m_flows.put(edge, 0d);
}
}

39. MaxFlow Class
5
public void updateResidual(List<Edge> path, double flow)
{
for (Edge edge : path) updateResidual(edge, flow);
d_maxFlow += flow;
}
public void updateResidual(Edge edge, double flow)
{
Double prev = m_flows.get(edge);
if (prev == null) prev = 0d;
m_flows.put(edge, prev + flow);
}
public double getResidual(Edge edge)
{
return edge.getWeight() - m_flows.get(edge);
}
public double getMaxFlow()
{
return d_maxFlow;
}

40. MaxFlow Class
5
public void updateResidual(List<Edge> path, double flow)
{
for (Edge edge : path) updateResidual(edge, flow);
d_maxFlow += flow;
}
public void updateResidual(Edge edge, double flow)
{
Double prev = m_flows.get(edge);
if (prev == null) prev = 0d;
m_flows.put(edge, prev + flow);
}
public double getResidual(Edge edge)
{
return edge.getWeight() - m_flows.get(edge);
}
public double getMaxFlow()
{
return d_maxFlow;
}

41. MaxFlow Class
5
public void updateResidual(List<Edge> path, double flow)
{
for (Edge edge : path) updateResidual(edge, flow);
d_maxFlow += flow;
}
public void updateResidual(Edge edge, double flow)
{
Double prev = m_flows.get(edge);
if (prev == null) prev = 0d;
m_flows.put(edge, prev + flow);
}
public double getResidual(Edge edge)
{
return edge.getWeight() - m_flows.get(edge);
}
public double getMaxFlow()
{
return d_maxFlow;
}

42. FordFulkerson Class
6
private Subgraph getAugmentingPath(Graph graph, MaxFlow mf,
Subgraph sub, int source, int target)
{
if (source == target) return sub;
Subgraph tmp;
for (Edge edge : graph.getIncomingEdges(target))
{
if (sub.contains(edge.getSource())) continue; // cycle
if (mf.getResidual(edge) <= 0) continue; // no residual
tmp = new Subgraph(sub);
tmp.addEdge(edge);
tmp = getAugmentingPath(graph, mf, tmp, source, edge.getSource());
if (tmp != null) return tmp;
}
return null;
}

43. FordFulkerson Class
6
private Subgraph getAugmentingPath(Graph graph, MaxFlow mf,
Subgraph sub, int source, int target)
{
if (source == target) return sub;
Subgraph tmp;
for (Edge edge : graph.getIncomingEdges(target))
{
if (sub.contains(edge.getSource())) continue; // cycle
if (mf.getResidual(edge) <= 0) continue; // no residual
tmp = new Subgraph(sub);
tmp.addEdge(edge);
tmp = getAugmentingPath(graph, mf, tmp, source, edge.getSource());
if (tmp != null) return tmp;
}
return null;
}
Complexity?

44. FordFulkerson Class
7
public MaxFlow getMaximumFlow(Graph graph, int source, int target)
{
MaxFlow mf = new MaxFlow(graph);
Subgraph sub = new Subgraph();
double min;
while ((sub = getAugmentingPath(graph, mf, sub, source, target)) != null)
{
min = getMin(mf, sub.getEdges());
mf.updateResidual(sub.getEdges(), min);
}
return mf;
}

45. FordFulkerson Class
7
public MaxFlow getMaximumFlow(Graph graph, int source, int target)
{
MaxFlow mf = new MaxFlow(graph);
Subgraph sub = new Subgraph();
double min;
while ((sub = getAugmentingPath(graph, mf, sub, source, target)) != null)
{
min = getMin(mf, sub.getEdges());
mf.updateResidual(sub.getEdges(), min);
}
return mf;
}

46. FordFulkerson Class
7
public MaxFlow getMaximumFlow(Graph graph, int source, int target)
{
MaxFlow mf = new MaxFlow(graph);
Subgraph sub = new Subgraph();
double min;
while ((sub = getAugmentingPath(graph, mf, sub, source, target)) != null)
{
min = getMin(mf, sub.getEdges());
mf.updateResidual(sub.getEdges(), min);
}
return mf;
}
private double getMin(MaxFlow mf, List<Edge> path)
{
double min = mf.getResidual(path.get(0));
for (int i=1; i<path.size(); i++)
min = Math.min(min, mf.getResidual(path.get(i)));
return min;
}

47. 2 2
2 2
Ford-Fulkerson: Backward Pushing
8
S
1
2
T1

48. 2 2
2 2
Ford-Fulkerson: Backward Pushing
8
S
1
2
T1

49. 2 2
2 2
Ford-Fulkerson: Backward Pushing
8
S
1
2
T1

50. 2 2
2 21
1
Ford-Fulkerson: Backward Pushing
8
S
1
2
T10

51. 2 2
2 21
1
Ford-Fulkerson: Backward Pushing
8
S
1
2
T10
1

52. 2 2
2 21
1
Ford-Fulkerson: Backward Pushing
8
S
1
2
T10
1

53. 2 2
2 21
1
Ford-Fulkerson: Backward Pushing
8
S
1
2
T10
1

54. 2 2
2 2
1
1
1
Ford-Fulkerson: Backward Pushing
8
S
1
2
T10
1
0

55. 2 2
2 2
1
1
1
Ford-Fulkerson: Backward Pushing
8
S
1
2
T10
1
1
0

56. 2 2
2 2
1
1
1
Ford-Fulkerson: Backward Pushing
8
S
1
2
T10
1
1
0

57. 2 2
2 2
1
1
1
Ford-Fulkerson: Backward Pushing
8
S
1
2
T10
1
1
0

58. 2 2
2 2
1
1
1
Ford-Fulkerson: Backward Pushing
8
S
1
2
T10
1
1
0
1 0

59. 2 2
2 2
1
1
1
Ford-Fulkerson: Backward Pushing
8
S
1
2
T10
1
1
0
1 0
1

60. 2 2
2 2
Ford-Fulkerson: Backward Pushing
9
S
1
2
T1

61. 2 2
2 2
Ford-Fulkerson: Backward Pushing
9
S
1
2
T1

62. 2 2
2 21
1
Ford-Fulkerson: Backward Pushing
9
S
1
2
T10

63. 2 2
2 21
1
Ford-Fulkerson: Backward Pushing
9
S
1
2
T10
1

64. 2 2
2 21
1
Ford-Fulkerson: Backward Pushing
9
S
1
2
T10
1
1
1
1

65. 2 2
2 21
1
Ford-Fulkerson: Backward Pushing
9
S
1
2
T10
1
1
1
1

66. 2 2
2 21
1
Ford-Fulkerson: Backward Pushing
9
S
1
2
T10
1
1
1
1

67. 2 2
2 2
1
1
1
Ford-Fulkerson: Backward Pushing
9
S
1
2
T10
1
1
1
10

68. 2 2
2 2
1
1
1
Ford-Fulkerson: Backward Pushing
9
S
1
2
T10
1
1
1
1
1
0

69. 2 2
2 2
1
1
1
Ford-Fulkerson: Backward Pushing
9
S
1
2
T10
1
1
1 12
1
1
0

70. 2 2
2 2
1
1
1
Ford-Fulkerson: Backward Pushing
9
S
1
2
T10
1
1
1 12
1
1
0

71. 2 2
2 2
1
1
1
Ford-Fulkerson: Backward Pushing
9
S
1
2
T10
1
1
1 12
1
1
0

72. 2 2
2 2
1
1
1
Ford-Fulkerson: Backward Pushing
9
S
1
2
T10
1
1
1
0
12
1
1
0
1
0

73. 2 2
2 2
1
1
1
Ford-Fulkerson: Backward Pushing
9
S
1
2
T10
1
1
1
0
12
1
1
0
1
0
1

74. 2 2
2 2
1
1
1
Ford-Fulkerson: Backward Pushing
9
S
1
2
T10
1
1
1
0
1
12
1
1
0
1
0
1
1
2

75. 2 2
2 2
1
1
1
Ford-Fulkerson: Backward Pushing
9
S
1
2
T10
1
1
1
0
1
12
1
1
0
1
0
1
1
2

76. 2 2
2 2
1
1
1
Ford-Fulkerson: Backward Pushing
9
S
1
2
T10
1
1
1
0
1
12
1
1
0
1
0
1
1
2

77. 2 2
2 2
1
1
1
Ford-Fulkerson: Backward Pushing
9
S
1
2
T10
1
1
1
0
1
12
1
1
0
1
0
1
1
2
0 0
22

78. 2 2
2 2
1
1
1
Ford-Fulkerson: Backward Pushing
9
S
1
2
T10
1
1
1
0
1
12
1
1
0
1
0
1
1
2
0 0
22
1

79. 2 2
2 2
1
1
1
Ford-Fulkerson: Backward Pushing
9
S
1
2
T10
1
1
1
0
1
12
1
1
0
1
0
1
1
2
0 0
22
1

80. protected void updateBackward(Graph graph, Subgraph sub, MaxFlow mf, double min)
{
boolean found;
for (Edge edge : sub.getEdges())
{
found = false;
for (Edge rEdge : graph.getIncomingEdges(edge.getSource()))
{
if (rEdge.getSource() == edge.getTarget())
{
mf.updateResidual(rEdge, -min);
found = true; break;
}
}
if (!found)
{
Edge rEdge = graph.setDirectedEdge
(edge.getTarget(), edge.getSource(), edge.getWeight());
mf.updateResidual(rEdge, -min);
}
}
}
10

81. protected void updateBackward(Graph graph, Subgraph sub, MaxFlow mf, double min)
{
boolean found;
for (Edge edge : sub.getEdges())
{
found = false;
for (Edge rEdge : graph.getIncomingEdges(edge.getSource()))
{
if (rEdge.getSource() == edge.getTarget())
{
mf.updateResidual(rEdge, -min);
found = true; break;
}
}
if (!found)
{
Edge rEdge = graph.setDirectedEdge
(edge.getTarget(), edge.getSource(), edge.getWeight());
mf.updateResidual(rEdge, -min);
}
}
}
10

82. protected void updateBackward(Graph graph, Subgraph sub, MaxFlow mf, double min)
{
boolean found;
for (Edge edge : sub.getEdges())
{
found = false;
for (Edge rEdge : graph.getIncomingEdges(edge.getSource()))
{
if (rEdge.getSource() == edge.getTarget())
{
mf.updateResidual(rEdge, -min);
found = true; break;
}
}
if (!found)
{
Edge rEdge = graph.setDirectedEdge
(edge.getTarget(), edge.getSource(), edge.getWeight());
mf.updateResidual(rEdge, -min);
}
}
}
10

83. Max-Flow Min-Cut Theorem
11

84. Max-Flow Min-Cut Theorem
11
• S-T cut

85. Max-Flow Min-Cut Theorem
11
• S-T cut
- A set of edges whose removal disconnects S to T.

86. Max-Flow Min-Cut Theorem
11
• S-T cut
- A set of edges whose removal disconnects S to T.
- The capacity of a cut = Σ c(e), ∀e in the cut.

87. Max-Flow Min-Cut Theorem
11
S
1
2
3
4
T
4
2
3
1
2
3
4
2
• S-T cut
- A set of edges whose removal disconnects S to T.
- The capacity of a cut = Σ c(e), ∀e in the cut.

88. Max-Flow Min-Cut Theorem
11
S
1
2
3
4
T
4
2
3
1
2
3
4
2
Minimum cut
• S-T cut
- A set of edges whose removal disconnects S to T.
- The capacity of a cut = Σ c(e), ∀e in the cut.

89. Max-Flow Min-Cut Theorem
11
S
1
2
3
4
T
4
2
3
1
2
3
4
2
Minimum cut
• S-T cut
- A set of edges whose removal disconnects S to T.
- The capacity of a cut = Σ c(e), ∀e in the cut.

90. Max-Flow Min-Cut Theorem
11
S
1
2
3
4
T
4
2
3
1
2
3
4
2
vs.
Maximum flow
Minimum cut
• S-T cut
- A set of edges whose removal disconnects S to T.
- The capacity of a cut = Σ c(e), ∀e in the cut.

91. Max-Flow Min-Cut Theorem
11
S
1
2
3
4
T
4
2
3
1
2
3
4
2
3
3
1
2
2
3
3
vs.
Maximum flow
Minimum cut
• S-T cut
- A set of edges whose removal disconnects S to T.
- The capacity of a cut = Σ c(e), ∀e in the cut.

92. Finding Min-Cut
12
4
4 2
S
1
2
3
4
T
2
3
1
2
3

93. Finding Min-Cut
12
4
4 2
S
1
2
3
4
T
2
3
1
2
3

94. Finding Min-Cut
12
4
4 2
S
1
2
3
4
T
2
3
1
2
3

95. Finding Min-Cut
12
4
4 22 0
S
1
2
3
4
T
2
3
1
2
3
1

96. Finding Min-Cut
12
4
4 22 0
S
1
2
3
4
T
2
3
1
2
3
1

97. Finding Min-Cut
12
4
4 22 0
S
1
2
3
4
T
2
3
1
2
3
1

98. Finding Min-Cut
12
4
4 22 0
S
1
2
3
4
T
2
3
1
2
3
1

99. Finding Min-Cut
12
43
4 22 01
S
1
2
3
4
T
2
3
1
2
3
10
0
2

100. Finding Min-Cut
12
43
4 22 01
S
1
2
3
4
T
2
3
1
2
3
10
0
2

101. Finding Min-Cut
12
43
4 22 01
S
1
2
3
4
T
2
3
1
2
3
10
0
2

102. Finding Min-Cut
12
43
4 22 01
S
1
2
3
4
T
2
3
1
2
3
10
0
2

103. Finding Min-Cut
12
431
4 22 01
S
1
2
3
4
T
2
3
1
2
3
10
0
2
0
0

104. Finding Min-Cut
12
431
4 22 01
S
1
2
3
4
T
2
3
1
2
3
10
0
2
0
0

105. Finding Min-Cut
12
431
4 22 01
S
1
2
3
4
T
2
3
1
2
3
10
0
2
0
0
• Algorithm

106. Finding Min-Cut
12
431
4 22 01
S
1
2
3
4
T
2
3
1
2
3
10
0
2
0
0
• Algorithm
1. Find a path p from S to T, remove any edge e in p, and put e to a set C.

107. Finding Min-Cut
12
431
4 22 01
S
1
2
3
4
T
2
3
1
2
3
10
0
2
0
0
• Algorithm
1. Find a path p from S to T, remove any edge e in p, and put e to a set C.
2. Repeat #1 until no path is found, and return C.

108. Finding Min-Cut
12
431
4 22 01
S
1
2
3
4
T
2
3
1
2
3
10
0
2
0
0
• Algorithm
1. Find a path p from S to T, remove any edge e in p, and put e to a set C.
2. Repeat #1 until no path is found, and return C.
• How can we find a min-cut?

109. Finding Min-Cut
12
431
4 22 01
S
1
2
3
4
T
2
3
1
2
3
10
0
2
0
0
• Algorithm
1. Find a path p from S to T, remove any edge e in p, and put e to a set C.
2. Repeat #1 until no path is found, and return C.
• How can we find a min-cut?
- Instead of removing any edge in #1, remove an edge with the
minimum original (not residual) weight.

110. Min-Cut vs. Max-Flow
13

111. Min-Cut vs. Max-Flow
13
• Lemma 1

112. Min-Cut vs. Max-Flow
13
• Lemma 1
- There is no extra edge in the min-cut.

113. Min-Cut vs. Max-Flow
13
• Lemma 1
- There is no extra edge in the min-cut.
- Prove?

114. Min-Cut vs. Max-Flow
13
• Lemma 1
- There is no extra edge in the min-cut.
- Prove?
• Lemma 2

115. Min-Cut vs. Max-Flow
13
• Lemma 1
- There is no extra edge in the min-cut.
- Prove?
• Lemma 2
- All edges in the min-cut must be parts of augmenting paths.

116. Min-Cut vs. Max-Flow
13
• Lemma 1
- There is no extra edge in the min-cut.
- Prove?
• Lemma 2
- All edges in the min-cut must be parts of augmenting paths.
- Prove?

117. Min-Cut vs. Max-Flow
13
• Lemma 1
- There is no extra edge in the min-cut.
- Prove?
• Lemma 2
- All edges in the min-cut must be parts of augmenting paths.
- Prove?
• Lemma 3

118. Min-Cut vs. Max-Flow
13
• Lemma 1
- There is no extra edge in the min-cut.
- Prove?
• Lemma 2
- All edges in the min-cut must be parts of augmenting paths.
- Prove?
• Lemma 3
- Each edge in the min-cut is the minimum weighted edge in each
augmenting path.

119. Min-Cut vs. Max-Flow
13
• Lemma 1
- There is no extra edge in the min-cut.
- Prove?
• Lemma 2
- All edges in the min-cut must be parts of augmenting paths.
- Prove?
• Lemma 3
- Each edge in the min-cut is the minimum weighted edge in each
augmenting path.
- Prove?

120. Network Flow Using Simplex
14
S
1
2
4
3
T
2
2

121. Network Flow Using Simplex
14
S
1
2
4
3
T
2
2
x1 x2
x3 x4

122. Network Flow Using Simplex
14
S
1
2
4
3
T
2
2
x1 x2
x3 x4
Max-Flow

123. Network Flow Using Simplex
14
S
1
2
4
3
T
2
2
x1 x2
x3 x4
Maximize:
Max-Flow

124. Network Flow Using Simplex
14
S
1
2
4
3
T
2
2
x1 x2
x3 x4
Maximize:
x2 + x4
Max-Flow

125. Network Flow Using Simplex
14
S
1
2
4
3
T
2
2
x1 x2
x3 x4
Maximize:
x2 + x4
Subject to:
Max-Flow

126. Network Flow Using Simplex
14
S
1
2
4
3
T
2
2
x1 x2
x3 x4
Maximize:
x2 + x4
Subject to:
x1 ≤ 4
x2 ≤ 2
x3 ≤ 3
x4 ≤ 2
x2 - x1 ≤ 0
x4 - x3 ≤ 0
Max-Flow

127. Network Flow Using Simplex
15
S
1
2
3
4
T
4
2
3
1
2
3
4
2

128. Network Flow Using Simplex
15
S
1
2
3
4
T
4
2
3
1
2
3
4
2
x1
x3
x6
x7
x2
x5
x8
x4

129. Network Flow Using Simplex
15
S
1
2
3
4
T
4
2
3
1
2
3
4
2
x1
x3
x6
x7
x2
x5
x8
x4
Maximize:

130. Network Flow Using Simplex
15
S
1
2
3
4
T
4
2
3
1
2
3
4
2
x1
x3
x6
x7
x2
x5
x8
x4
Maximize: Subject to:

131. Network Flow Using Simplex
15
S
1
2
3
4
T
4
2
3
1
2
3
4
2
x1
x3
x6
x7
x2
x5
x8
x4
Maximize: Subject to:
x7 + x8

132. Network Flow Using Simplex
15
S
1
2
3
4
T
4
2
3
1
2
3
4
2
x1
x3
x6
x7
x2
x5
x8
x4
Maximize: Subject to:
x7 + x8 x3 - x1 ≤ 0
x4 + x5 - x2 - x6 ≤ 0
x6 + x7 - x3 - x4 ≤ 0
x8 - x5 ≤ 0
x1 ≤ 4
x2 ≤ 2
x3 ≤ 3
x4 ≤ 2
x5 ≤ 3
x6 ≤ 1
x7 ≤ 2
x8 ≤ 4

133. Network Flow Using Simplex
16
S
1
2
4
3
T
2
2
x1 x2
x3 x4
Maximize:
x2 + x4
Subject to:
x1 ≤ 4
x2 ≤ 2
x3 ≤ 3
x4 ≤ 2
x2 - x1 ≤ 0
x4 - x3 ≤ 0
Max-Flow

134. Network Flow Using Simplex
16
S
1
2
4
3
T
2
2
x1 x2
x3 x4
Maximize:
x2 + x4
Subject to:
x1 ≤ 4
x2 ≤ 2
x3 ≤ 3
x4 ≤ 2
x2 - x1 ≤ 0
x4 - x3 ≤ 0
Max-Flow Min-Cut

135. Network Flow Using Simplex
16
S
1
2
4
3
T
2
2
x1 x2
x3 x4
Maximize:
x2 + x4
Subject to:
x1 ≤ 4
x2 ≤ 2
x3 ≤ 3
x4 ≤ 2
x2 - x1 ≤ 0
x4 - x3 ≤ 0
Max-Flow Min-Cut
Minimize:

136. Network Flow Using Simplex
16
S
1
2
4
3
T
2
2
x1 x2
x3 x4
Maximize:
x2 + x4
Subject to:
x1 ≤ 4
x2 ≤ 2
x3 ≤ 3
x4 ≤ 2
x2 - x1 ≤ 0
x4 - x3 ≤ 0
Max-Flow Min-Cut
Minimize:
4x1 + 2x2 + 3x3 + 2x4

137. Network Flow Using Simplex
16
S
1
2
4
3
T
2
2
x1 x2
x3 x4
Maximize:
x2 + x4
Subject to:
x1 ≤ 4
x2 ≤ 2
x3 ≤ 3
x4 ≤ 2
x2 - x1 ≤ 0
x4 - x3 ≤ 0
Max-Flow Min-Cut
Minimize:
4x1 + 2x2 + 3x3 + 2x4
Subject to:

138. Network Flow Using Simplex
16
S
1
2
4
3
T
2
2
x1 x2
x3 x4
Maximize:
x2 + x4
Subject to:
x1 ≤ 4
x2 ≤ 2
x3 ≤ 3
x4 ≤ 2
x2 - x1 ≤ 0
x4 - x3 ≤ 0
Max-Flow Min-Cut
Minimize:
4x1 + 2x2 + 3x3 + 2x4
Subject to:
x1 + y1 ≥ 1
x3 + y3 ≥ 1
x2 - y1 ≥ 0
x4 - y3 ≥ 0

139. Network Flow Using Simplex
17
S
1
2
3
4
T
4
2
3
1
2
3
4
2

140. Network Flow Using Simplex
17
S
1
2
3
4
T
4
2
3
1
2
3
4
2
x1
x3
x6
x7
x2
x5
x8
x4

141. Network Flow Using Simplex
17
S
1
2
3
4
T
4
2
3
1
2
3
4
2
x1
x3
x6
x7
x2
x5
x8
x4
Minimize:

142. Network Flow Using Simplex
17
S
1
2
3
4
T
4
2
3
1
2
3
4
2
x1
x3
x6
x7
x2
x5
x8
x4
Minimize: Subject to:

143. Network Flow Using Simplex
17
S
1
2
3
4
T
4
2
3
1
2
3
4
2
x1
x3
x6
x7
x2
x5
x8
x4
Minimize: Subject to:
4x1 + 2x2 + 3x3 + 2x4 +
3x5 + x6 + 2x7 + 4x8

144. Network Flow Using Simplex
17
S
1
2
3
4
T
4
2
3
1
2
3
4
2
x1
x3
x6
x7
x2
x5
x8
x4
Minimize: Subject to:
4x1 + 2x2 + 3x3 + 2x4 +
3x5 + x6 + 2x7 + 4x8
x1 + y1 ≥ 1
x2 + y2 ≥ 1
x3 - y1 + y3 ≥ 0
x4 - y2 + y3 ≥ 0
x5 - y2 + y4 ≥ 0
x6 - y3 + y2 ≥ 0
x7 - y3 ≥ 0
x8 - y4 ≥ 0