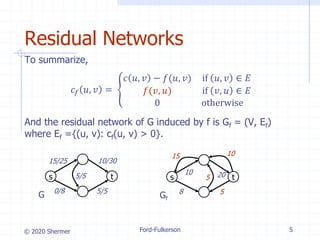
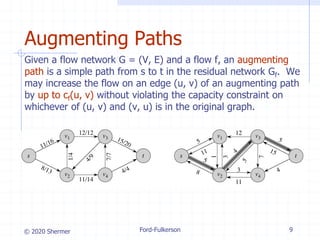
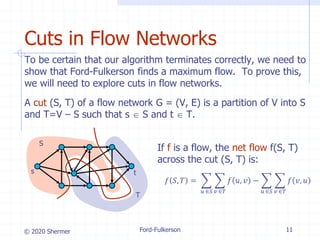
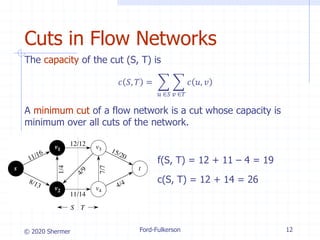
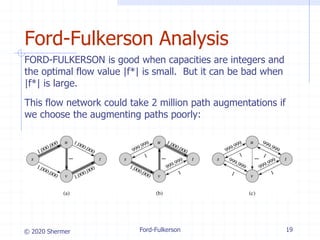
The document provides an overview of the Ford-Fulkerson method for computing the maximum flow in flow networks, detailing concepts such as residual networks, augmenting paths, and cuts. It discusses the algorithm's iterative process that increases flow and introduces the Edmonds-Karp algorithm as an efficient implementation using breadth-first search for path selection. The analysis covers the time complexities of both the Ford-Fulkerson method and the Edmonds-Karp algorithm, highlighting their performance under varying conditions.