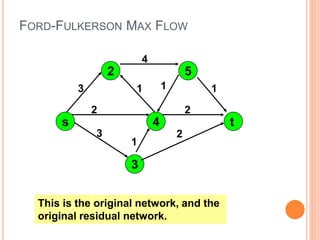
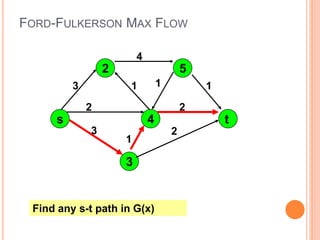
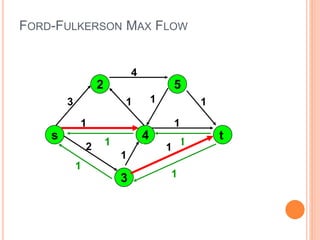
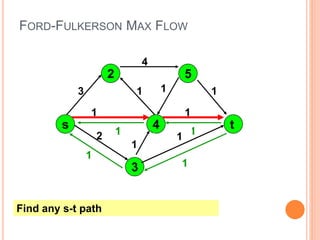
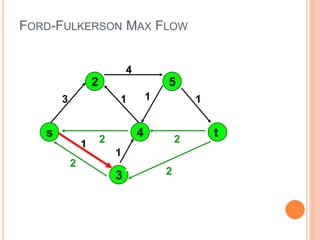
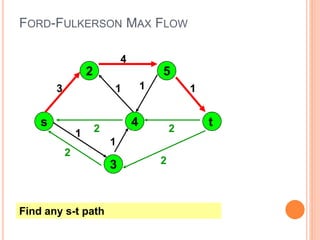
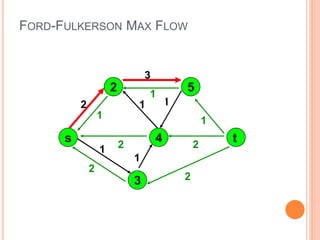
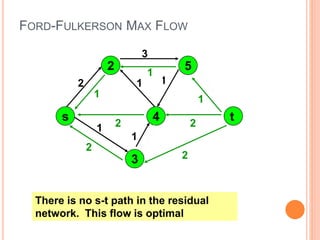
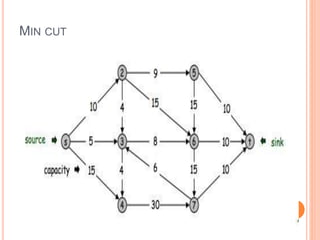
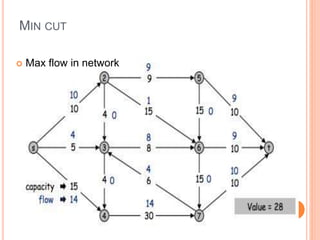
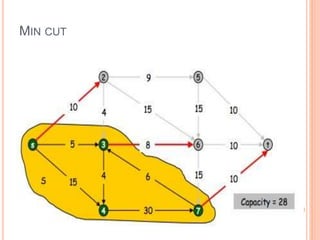
The document presents a maximum flow min cut theorem that optimizes network performance by introducing the max flow theorem and the Ford-Fulkerson algorithm. It explains how to determine maximum flow in directed, weighted graphs through the construction of a residual graph and updates until maximal flow is achieved. Additionally, it discusses the importance of cuts in network flow and applications in various fields such as traffic problems and data mining.

1. A MAXIMUM FLOW MIN CUT
THEOREM FOR OPTIMIZING
NETWORK
Shethwala Ridhvesh

2. OUTLINES
Introduction
Max flow theorem
Ford-Fulkerson algorithm
Min cut theorem
Conclusion
References

4. MAX FLOW THEOREM
-> A directed, weighted graph is called a (flow) network.
-> Each edge has a weight and direction.
-> We assume there exists a source and a sink.
 The flow over a network is a function f: E -> R,
assigning values to each of the edges in the network
which are nonnegative and less than the capacity of that
edge. For each intermediate vertex, the outflow and
inflow must be equal.
 The value of this flow is the total amount leaving the
source (and thus entering the sink).

5. FORD-FULKERSON MAX FLOW
The Ford-Fulkerson algorithm for finding
the maximum flow:
a. Construct the Residual Graph
b. Find a path from the source to the sink with
strictly positive flow.
c. If this path exists, update flow to include it. Go
to Step a.
d. Else, the flow is maximal.
e. The (s,t)-cut has as S all vertices reachable from
the source, and T as V - S.

6. FORD-FULKERSON MAX FLOW
4
11
2
2
1
2
3
3
1
s
2
4
5
3
t
This is the original network, and the
original residual network.

7. 4
11
2
2
1
2
3
3
1
FORD-FULKERSON MAX FLOW
Find any s-t path in G(x)
s
2
4
5
3
t

8. 4
1
1
2
1
3
FORD-FULKERSON MAX FLOW
11
1
2
1
2
3
2
1
s
2
4
5
3
t

9. 4
1
1
2
1
3
FORD-FULKERSON MAX FLOW
Find any s-t path
11
1
2
1
2
3
2
1
s
2
4
5
3
t

10. 4
2
1
1
1
1
2
2
1
1
1
1
3
FORD-FULKERSON MAX FLOW
11
1
1
3
2
1
s
2
4
5
3
t

11. 4
2
1
1
1
1
2
2
1
1
1
1
3
FORD-FULKERSON MAX FLOW
11
1
1
3
2
1
s
2
4
5
3
t
Find any s-t path

12. 1
1 1
11
4
1
2
1
1
2
1
1
3
FORD-FULKERSON MAX FLOW
113
2
1
s
2
4
5
3
t

13. 1
1 1
11
4
1
2
1
1
2
2
1
1
3
FORD-FULKERSON MAX FLOW
113
2
1
s
2
4
5
3
t
Find any s-t path

14. 1
1
1
2
1 1
11
4
2
2
1
1
2
2
1
FORD-FULKERSON MAX FLOW
113
1
1
s
2
4
5
3
t
2

15. 1
1
2
1 1
11
4
2
2
1
1
2
2
1
FORD-FULKERSON MAX FLOW
113
1
1
s
2
4
5
3
t
Find any s-t path
2

16. 11
1
1
1
4
13
1
1
2
1 1
3
2
2
1
2
1
FORD-FULKERSON MAX FLOW
2
1
s
2
4
5
3
t
2

17. 11
1
1
1
4
13
1
1
2 1 1
3
2
2
1
2
1
FORD-FULKERSON MAX FLOW
2
1
s
2
4
5
3
t
2
There is no s-t path in the residual
network. This flow is optimal

18. 11
1
1
1
4
13
1
1
2
1 1
3
2
2
1
2
1
FORD-FULKERSON MAX FLOW
2
1
s
2
4
5
3
t
2
These are the nodes that are reachable
from node s.
s
2
4
5
3

19. FORD-FULKERSON MAX FLOW
1
1
2
2
2
1
2
s
2
4
5
3
t
Here is the optimal flow

20. MIN CUT
 A cut is a partition of the vertices into disjoint
subsets S and T. In a flow network, the source is
located in S, and the sink is located in T.
 The cut-set of a cut is the set of edges that begin
in S and end in T.
 The capacity of a cut is sum of the weights
of the edges beginning in S and ending in T.

21. MIN CUT

22. MIN CUT
 Max flow in network

23. MIN CUT

24. APPLICATIONS
- Traffic problem on road
- Data Mining
- Distributed Computing
- Image processing
- Project selection
- Bipartite Matching

25. CONCLUSION
 Using this Max-flow min-cut theorem we can
maximize the flow in network and can use the
maximum capacity of route for optimizing network.

26. REFERENCES
 Ford, Jr., L. R., and D. R. Fulkerson. “Maximal Flow
Through a Network.” Canadian Journal of Mathematics
8 (1956): 399-404. Canadian Mathematical Society.
Web. 2 June,2010
 Ellis L. Johnson, Committee Chair, George L.
Nemhauser: Shortest paths and multicommodity
network flow,2003
 FORD.L.R. AND D. R. FULKERSON 1956. Maximal
Flow Through a Network. Can. J. Math. 8,399-404.
 Cormen, Thomas H. Introduction to Algorithms. 2nd ed.
Cambridge, Massachusetts: MIT, 2001