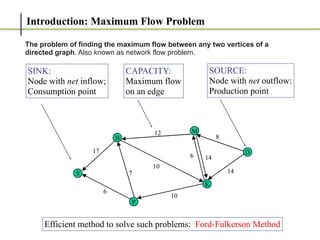
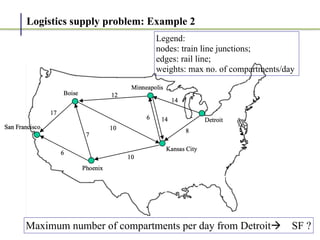
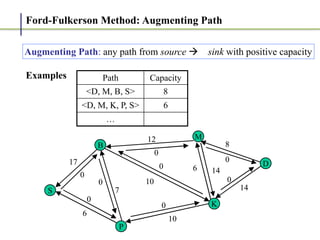
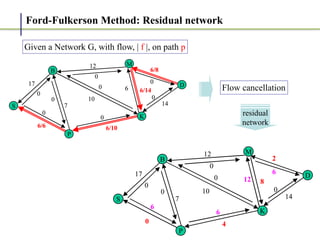
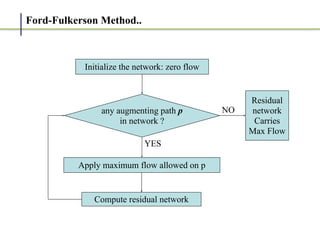
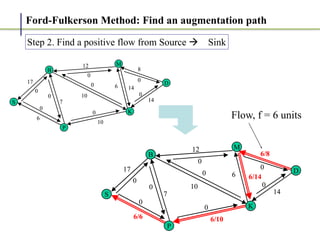
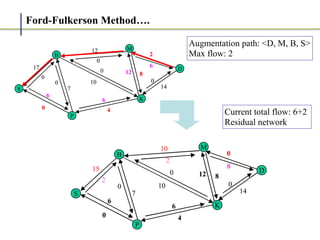
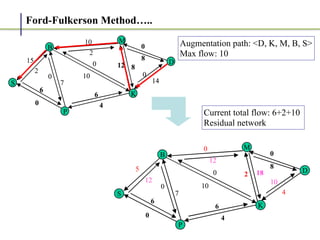
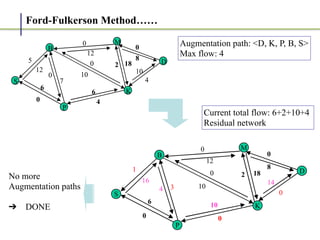
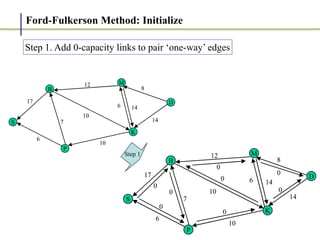
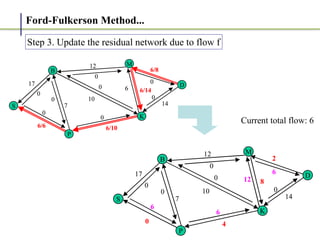
1. The Ford-Fulkerson method is an algorithm for finding the maximum flow in a flow network, also known as the maximum flow problem. 2. It works by finding augmenting paths in the residual network - paths from the source to the sink with available capacity. It then pushes additional flow along this path. 3. The key steps are: (1) finding an augmenting path, (2) updating the residual capacities and flows, (3) repeating until no more augmenting paths exist. This guarantees finding the maximum possible flow.

1. Himanshu Moliya
Ford Fulkerson
A Method to compute maximum flow
Key Words: Maximum Flow, Graph algorithm, Advanced algorithm

2. Introduction: Maximum Flow Problem
D
M
K
S
B
P
8
14
14
6
12
10
10
7
17
6
D
M
K
S
B
P
8
14
14
6
12
10
10
7
17
6
SOURCE:
Node with net outflow:
Production point
SINK:
Node with net inflow;
Consumption point
CAPACITY:
Maximum flow
on an edge
Efficient method to solve such problems: Ford-Fulkerson Method
The problem of finding the maximum flow between any two vertices of a
directed graph. Also known as network flow problem.

3. Ford-Fulkerson Method
Three fundamental concepts:
1. Flow cancellation
2. Augmentation flow
3. Residual network

4. Ford-Fulkerson Method: Flow Cancellation
a b
14
6
Net flows:
5/14
3/6
a b
2/14
6
a b
Additional 7 units from b ! a ?!
14
5/6
a b
Network
Flow: 5 units, a ! b, 3 units b ! a
Flow Cancellation: Compute the NET FLOW between a pair of nodes

5. Ford-Fulkerson Method: Augmenting Path
Augmenting Path: any path from source ! sink with positive capacity
Examples
8
14
14
6
12
10
10
7
17
6
0
0
0
0
0
0
0
0
D
M
K
S
B
P
8
14
14
6
12
10
10
7
17
6
0
0
0
0
0
0
0
0
D
M
K
S
B
P
Path Capacity
<D, M, B, S> 8
<D, M, K, P, S> 6
…

6. Ford-Fulkerson Method: Residual network
6/8
14
6/14
6
12
10
6/10
7
17
6/6
0
0
0
0
0
0
0
0
D
M
K
S
B
P
6/8
14
6/14
6
12
10
6/10
7
17
6/6
0
0
0
0
0
0
0
0
D
M
K
S
B
P
2
14
8
12
12
10
4
7
17
0
0
6
0
0
0
6
0
6
D
M
K
S
B
P
2
14
8
12
12
10
4
7
17
0
0
6
0
0
0
6
0
6
D
M
K
S
B
P
Given a Network G, with flow, | f |, on path p
Flow cancellation
residual
network

7. Ford-Fulkerson Method..
Initialize the network: zero flow
any augmenting path p
in network ?
Apply maximum flow allowed on p
Compute residual network
Residual
network
Carries
Max Flow
YES
NO

8. Ford-Fulkerson Method: Initialize
Step 1. Add 0-capacity links to pair ‘one-way’ edges
D
M
K
S
B
P
8
14
14
6
12
10
10
7
17
6
D
M
K
S
B
P
8
14
14
6
12
10
10
7
17
6
8
14
14
6
12
10
10
7
17
6
0
0
0
0
0
0
0
0
D
M
K
S
B
P
8
14
14
6
12
10
10
7
17
6
0
0
0
0
0
0
0
0
D
M
K
S
B
P
Step 1

9. Ford-Fulkerson Method: Find an augmentation path
8
14
14
6
12
10
10
7
17
6
0
0
0
0
0
0
0
0
D
M
K
S
B
P
8
14
14
6
12
10
10
7
17
6
0
0
0
0
0
0
0
0
D
M
K
S
B
P
6/8
14
6/14
6
12
10
6/10
7
17
6/6
0
0
0
0
0
0
0
0
D
M
K
S
B
P
6/8
14
6/14
6
12
10
6/10
7
17
6/6
0
0
0
0
0
0
0
0
D
M
K
S
B
P
Flow, f = 6 units
Step 2. Find a positive flow from Source ! Sink

10. Ford-Fulkerson Method...
6/8
14
6/14
6
12
10
6/10
7
17
6/6
0
0
0
0
0
0
0
0
D
M
K
S
B
P
6/8
14
6/14
6
12
10
6/10
7
17
6/6
0
0
0
0
0
0
0
0
D
M
K
S
B
P
2
14
8
12
12
10
4
7
17
0
0
6
0
0
0
6
0
6
D
M
K
S
B
P
2
14
8
12
12
10
4
7
17
0
0
6
0
0
0
6
0
6
D
M
K
S
B
P
Step 3. Update the residual network due to flow f
Current total flow: 6

11. Ford-Fulkerson Method….
2
14
8
12
12
10
4
7
17
0
0
6
0
0
0
6
0
6
D
M
K
S
B
P
2
14
8
12
12
10
4
7
17
0
0
6
0
0
0
6
0
6
D
M
K
S
B
P
Augmentation path: <D, M, B, S>
Max flow: 2
Current total flow: 6+2
Residual network
0
14
8
12
10
4
7
15
0
2
6
0
0
8
0
6
D
M
K
S
B
P
14
8
12
10
10
4
7
0
6
0
0
2
0
6

12. Ford-Fulkerson Method…..
0
14
8
12
10
4
7
15
0
2
6
0
0
8
0
6
D
M
K
S
B
P
14
8
12
10
10
4
7
0
6
0
0
2
0
6
0
18
2
10
4
7
5
0
12
6
0
0
8
10
6
D
M
K
S
B
P
4
0
10
7
0
0
12
Augmentation path: <D, K, M, B, S>
Max flow: 10
Current total flow: 6+2+10
Residual network

13. Ford-Fulkerson Method……
0
18
2
10
4
7
5
0
12
6
0
0
8
10
6
D
M
K
S
B
P
4
0
10
7
0
0
12
0
18
2
10
0
1
0
16
6
0
8
14
10
D
M
K
S
B
P
0
0
10
3
4
0
12
Augmentation path: <D, K, P, B, S>
Max flow: 4
Current total flow: 6+2+10+4
Residual network
No more
Augmentation paths
➔ DONE

14. Programmatic implementation steps
Ford-Fulkerson Algorithm
1) Start with initial flow as 0.
2) While there is a augmenting path from source to sink.
Add this path-flow to flow.
3) Return flow.
Time Complexity:
• Time complexity of the above algorithm is O(max_flow * E)
• We run a loop while there is an augmenting path.
• In worst case, we may add 1 unit flow in every iteration. Therefore the time
complexity becomes O(max_flow * E).

15. Concluding remarks
Applications:
(i) Transportation Logistics (ships, airlines, trains)
(ii) Design of supply networks
(water, sewage, chemical plant, food processing, roads)

16. Logistics supply problem: Example 1
What is the maximum power we can supply to Wan Chai for a Light-n-Sound Show?
Lamma
Power Station
W
a
n
C
h
a
i
NorthPoint
RepulseBay
Aberdeen
PokFuLam
Western
Central
HappyValley
30
50
40
20
20
20
20
10
20
5
40
15 15
40
25
15
20
Legend:
Node: Sub-station
Edge: Power line
Weight: Line capacity

17. Logistics supply problem: Example 2
Legend:
nodes: train line junctions;
edges: rail line;
weights: max no. of compartments/day
Maximum number of compartments per day from Detroit! SF ?

18. Survey / publications (References)
• Ford, Lester Randolph and Fulkerson, D. R.. Flows in Networks,
Princeton: Princeton University Press, 2015. https://doi.org/
10.1515/9781400875184
• Ballarin, C.: Interpretation of locales in Isabelle: theories and proof
contexts. In: Borwein, J.M., Farmer, W.M. (eds.) MKM 2006. LNCS
(LNAI), vol. 4108, pp. 31–43. Springer, Heidelberg (2006)
• Bertot, Y., Castran, P., Proving, I.T., Development, P.: Coq’Art The
Calculus of Inductive Constructions, 1st edn. Springer (2010)

19. Himanshu Moliya
himanshuvmoliya@gmail.com
Thank you!