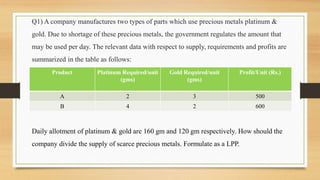
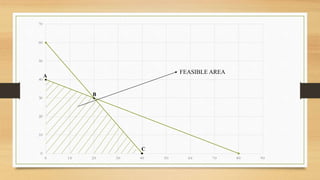
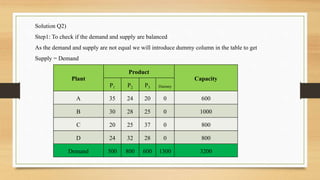
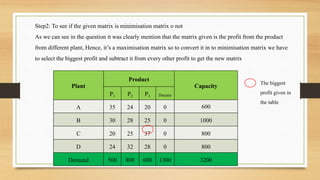
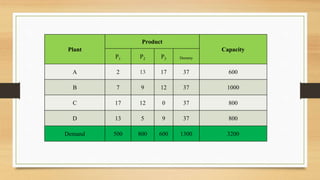
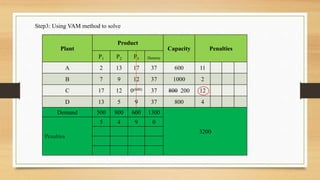
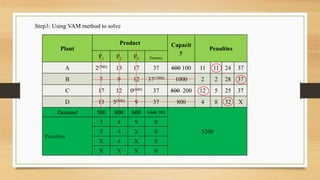
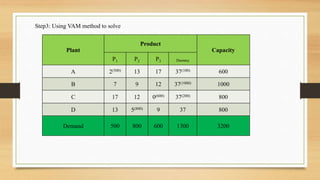
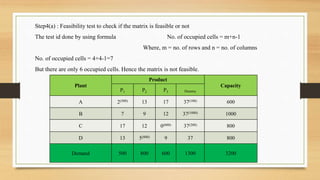
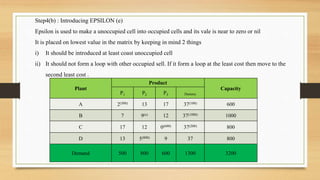
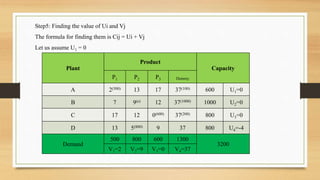
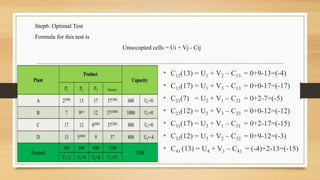
This document presents a linear programming problem and a transportation problem to determine the optimal allocation of scarce resources and plant location. For the linear programming problem, the optimal solution is to produce 20 units of Product A and 30 units of Product B, using a total of 140 units of platinum and 120 units of gold. For the transportation problem, setting up the new plant in city D would maximize aggregate profits at Rs. 43,100, compared to Rs. 39,700 if located in city C. The optimal solution is to locate the new plant in city D.

1. Operations Research

2. “
”
CES Activity On LLP and Transportation
Problems
Made By :- ADITYA ARORA
Roll No. :- 0141mba009
Class :- MBA 3A

3. Linear Programming
Problems
Graphic Method

4. Product Platinum Required/unit
(gms)
Gold Required/unit
(gms)
Profit/Unit (Rs.)
A 2 3 500
B 4 2 600
Q1) A company manufactures two types of parts which use precious metals platinum &
gold. Due to shortage of these precious metals, the government regulates the amount that
may be used per day. The relevant data with respect to supply, requirements and profits are
summarized in the table as follows:
Daily allotment of platinum & gold are 160 gm and 120 gm respectively. How should the
company divide the supply of scarce precious metals. Formulate as a LPP.

5. Solution Q1)
After reading the question we know this is a maximization question as we have a limited
supply of Gold and Platinum for 2 product which required the item to produce the product
Let us assume product A is x1 and product B is x2
Therefor,
Zmax = 500 x1 + 600x2

6. For the equation we know that Gold and Platinum daily allotment is 120gm and 160gm .
Now, for equation-1 we will take all the requirement of platinum per unit of all product witch will be
multiplied with the units to be allotted to a product (i.e., x1 and x2) and then add them with each other witch
will be less then or equal to zero(0)
i.e., 2x1+ 4x2≤ 160
Now, for equation-2 we will take all the requirement of gold per unit of all product witch will be multiplied
with the units to be allotted to a product (i.e., x1 and x2) and then add them with each other witch will be less
then or equal to zero(0)
i.e., 3x1+ 2x2≤ 120
Also a non-negativity restriction for preventing negative values i.e., x1 ,x2 ≥ 0

7. By the help of eq. 1 we will find out the coordinates
2x1+ 4x2≤ 160
Let take x1 =0
0+ 4x2= 160
x2= 40
Therefor, coordinates are (0,40)
Let take x2 =0
2x1+ 0 = 160
x1= 80
Therefor, coordinates are (80,0)
x1 x2
0 40
80 0

8. By the help of eq. 2 we will find out the coordinates
3x1+ 2x2≤ 120
Let take x1 =0
0+ 2x2= 120
x2= 60
Therefor, coordinates are (0,60)
Let take x2 =0
3x1+ 0 = 120
x1= 40
Therefor, coordinates are (40,0)
x1 x2
0 60
40 0

9. 0
10
20
30
40
50
60
70
0 10 20 30 40 50 60 70 80 90
A
B
C
FEASIBLE AREA

10. From the graph we got the fishable area OABC and thehe coordinate are
We will use equation of zmax to find the quantity per product
Zmax = 500 x1 + 600x2
• For O
Zmax = 0
• For A
Zmax = 0x1 + (600*40)
Zmax = 24000
• For B
Zmax = (500*20) + (600*30)
Zmax = 28000
x1 x2
O 0 0
A 0 40
B 20 30
C 40 0
• For C
Zmax = 500*40 + 0x2
Zmax = 20000

11. As the value of coordinate C is the maximum, therefor, the producer should use
• For product A = 20 units of Platinum and 20 unit of Gold and
• For product B = 30 units of Platinum and 30 units of Gold
Therefor, making total of 140 units of Platinum and 120units of Gold

12. Any Questions
Relating To LLP

13. Transportation Problem

14. Q2) A company is producing three product P1, P2 and P3 at two of its plant situated in cities A and B. The
company plans to start a new plant in city C or in city D. the unit profits from the various plants are listed
in the table, along with the demand for various products and capacity available in each of the plants.
Plant
Product
Capacity
P1 P2 P3
A 35 24 20 600
B 30 28 25 1000
C 20 25 37 800
D 24 32 28 800
Demand 500 800 600 1900 3200
The company would set up the new plant on the bases of maximising aggregate profits from the three
cities plants. Using the transportation method determine in witch city would the plant be set up and
what would the corresponding profit be.

15. Solution Q2)
Step1: To check if the demand and supply are balanced
As the demand and supply are not equal we will introduce dummy column in the table to get
Supply = Demand
Plant
Product
Capacity
P1 P2 P3 Dummy
A 35 24 20 0 600
B 30 28 25 0 1000
C 20 25 37 0 800
D 24 32 28 0 800
Demand 500 800 600 1300 3200

16. Step2: To see if the given matrix is minimisation matrix o not
As we can see in the question it was clearly mention that the matrix given is the profit from the product
from different plant, Hence, it’s a maximisation matrix so to convert it in to minimisation matrix we have
to select the biggest profit and subtract it from every other profit to get the new matrix
Plant
Product
Capacity
P1 P2 P3 Dummy
A 35 24 20 0 600
B 30 28 25 0 1000
C 20 25 37 0 800
D 24 32 28 0 800
Demand 500 800 600 1300 3200
The biggest
profit given in
the table

17. Plant
Product
Capacity
P1 P2 P3 Dummy
A 2 13 17 37 600
B 7 9 12 37 1000
C 17 12 0 37 800
D 13 5 9 37 800
Demand 500 800 600 1300 3200

18. Step3: Using VAM method to solve
Plant
Product
Capacity Penalties
P1 P2 P3 Dummy
A 2 13 17 37 600 11
B 7 9 12 37 1000 2
C 17 12 0(600) 37 800 200 12
D 13 5 9 37 800 4
Demand 500 800 600 1300
3200
Penalties
5 4 9 0

19. Step3: Using VAM method to solve
Plant
Product
Capacity Penalties
P1 P2 P3 Dummy
A 2(500) 13 17 37 600 100 11 11
B 7 9 12 37 1000 2 2
C 17 12 0(600) 37 800 200 12 5
D 13 5 9 37 800 4 8
Demand 500 800 600 1300
3200
Penalties
5 4 9 0
5 4 X 0

20. Step3: Using VAM method to solve
Plant
Product
Capacity Penalties
P1 P2 P3 Dummy
A 2(500) 13 17 37 600 100 11 11 24
B 7 9 12 37 1000 2 2 28
C 17 12 0(600) 37 800 200 12 5 25
D 13 5(800) 9 37 800 4 8 32
Demand 500 800 600 1300
3200
Penalties
5 4 9 0
5 4 X 0
X 4 X 0

21. Step3: Using VAM method to solve
Plant
Product Capacit
y
Penalties
P1 P2 P3 Dummy
A 2(500) 13 17 37 600 100 11 11 24 37
B 7 9 12 37(1000) 1000 2 2 28 37
C 17 12 0(600) 37 800 200 12 5 25 37
D 13 5(800) 9 37 800 4 8 32 X
Demand 500 800 600 1300 300
3200
Penalties
5 4 9 0
5 4 X 0
X 4 X 0
X X X 0

22. Step3: Using VAM method to solve
Plant
Product Capacit
y
Penalties
P1 P2 P3 Dummy
A 2(500) 13 17 37(100) 600 100 11 11 24 37
B 7 9 12 37(1000) 1000 2 2 28 37
C 17 12 0(600) 37(200) 800 200 12 5 25 37
D 13 5(800) 9 37 800 4 8 32 X
Demand 500 800 600 1300 300
3200
Penalties
5 4 9 0
5 4 X 0
X 4 X 0
X X X 0

23. Step3: Using VAM method to solve
Plant
Product
Capacity
P1 P2 P3 Dummy
A 2(500) 13 17 37(100) 600
B 7 9 12 37(1000) 1000
C 17 12 0(600) 37(200) 800
D 13 5(800) 9 37 800
Demand 500 800 600 1300 3200

24. Step4(a) : Feasibility test to check if the matrix is feasible or not
The test id done by using formula No. of occupied cells = m+n-1
Where, m = no. of rows and n = no. of columns
No. of occupied cells = 4+4-1=7
But there are only 6 occupied cells. Hence the matrix is not feasible.
Plant
Product
Capacity
P1 P2 P3 Dummy
A 2(500) 13 17 37(100) 600
B 7 9 12 37(1000) 1000
C 17 12 0(600) 37(200) 800
D 13 5(800) 9 37 800
Demand 500 800 600 1300 3200

25. Step4(b) : Introducing EPSILON (e)
Epsilon is used to make a unoccupied cell into occupied cells and its vale is near to zero or nil
It is placed on lowest value in the matrix by keeping in mind 2 things
i) It should be introduced at least coast unoccupied cell
ii) It should not form a loop with other occupied sell. If it form a loop at the least cost then move to the
second least cost .
Plant
Product
Capacity
P1 P2 P3 Dummy
A 2(500) 13 17 37(100) 600
B 7 9(e) 12 37(1000) 1000
C 17 12 0(600) 37(200) 800
D 13 5(800) 9 37 800
Demand 500 800 600 1300 3200

26. Step5: Finding the value of Ui and Vj
The formula for finding them is Cij = Ui + Vj
Let us assume U1 = 0
Plant
Product
Capacity
P1 P2 P3 Dummy
A 2(500) 13 17 37(100) 600 U1=0
B 7 9(e) 12 37(1000) 1000 U2=0
C 17 12 0(600) 37(200) 800 U3=0
D 13 5(800) 9 37 800 U4=-4
Demand
500 800 600 1300
3200
V1=2 V2=9 V3=0 V4=37

27. Step6: Optimal Test
Formula for this test is
Unoccupied cells = Ui + Vj - Cij
• C12(13) = U1 + V2 – C13 = 0+9-13=(-4)
• C13(17) = U1 + V3 – C13 = 0+0-17=(-17)
• C21(7) = U2 + V1 – C21 = 0+2-7=(-5)
• C23(12) = U2 + V3 – C23 = 0+0-12=(-12)
• C31(17) = U3 + V1 – C31 = 0+2-17=(-15)
• C32(12) = U3 + V2 – C32 = 0+9-12=(-3)
• C41 (13) = U4 + V1 – C41 = (-4)+2-13=(-15)

28. Step6: Optimal Test
Formula for this test is
Unoccupied cells = Ui + Vj - Cij
• C43 (9) = U4 + V3 – C43 = (-4)+0-9=(-13)
• C44 (37) = U4 + V4 – C44 = (-4)+37-37=(-4)
As all the values of optimal cost is negative
or zero, Therefor, the new shold be set up
in

29. If we take cities A,B and C the profit will be
Total profit (ABC) = (35*500)+(0*100)+(28*e)+(0*1000)+(37*600)+(0*200)= 17500+0+0+0+22200+0 =39700
If we take cities A,B and D the profit will be
Total profit (ABD) = (35*500)+(0*100)+(28*e)+(0*1000)+(32*800)= 17500+0+0+0+25600 =43100

30. • As the Profit earned is more in cities ABD then in cities ABC i.e., 43100 and
39700 respectively
• Therefor, the new plant should be setup in city D rather then in City C

31. Thank You
Any Questions