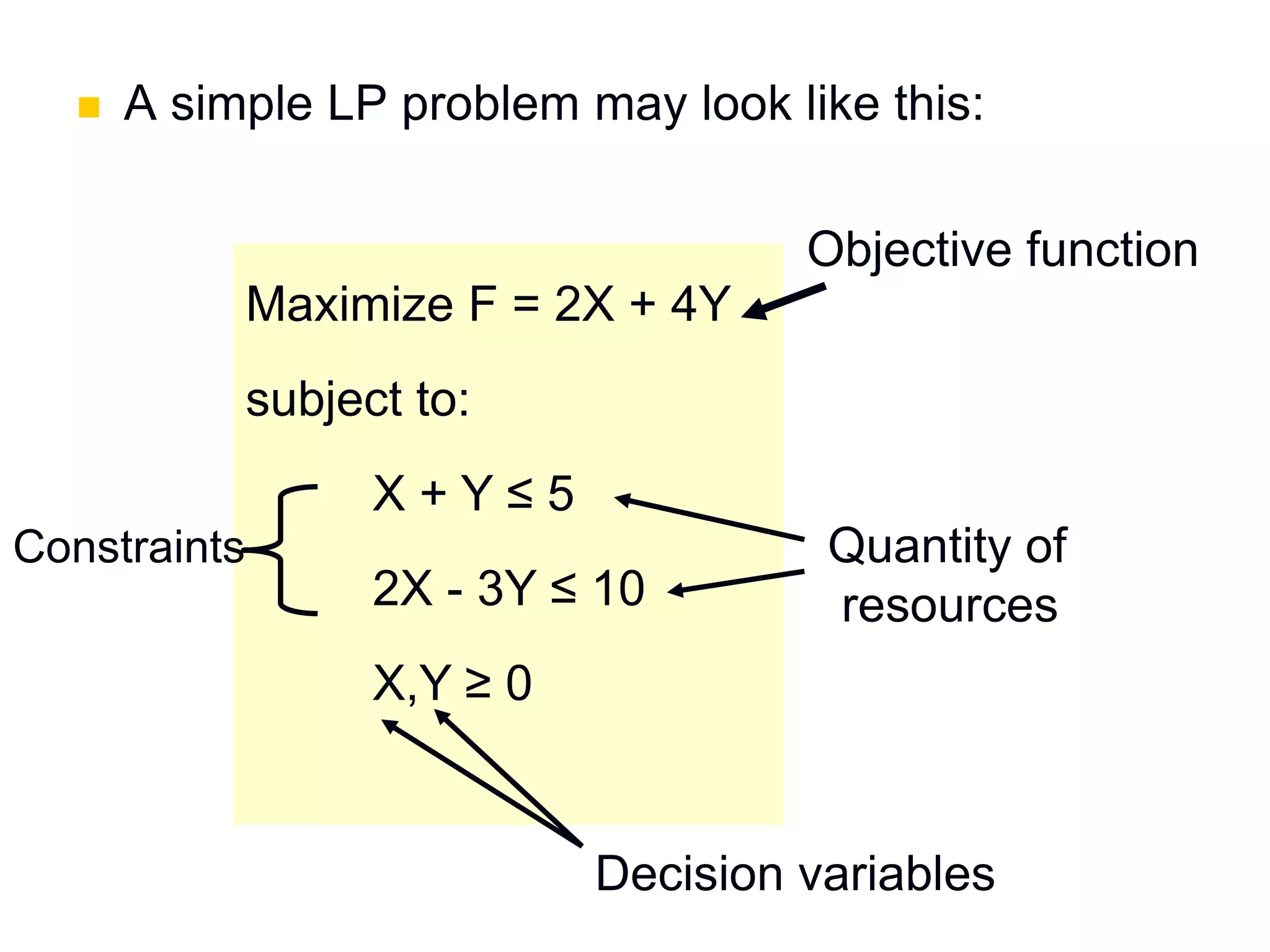
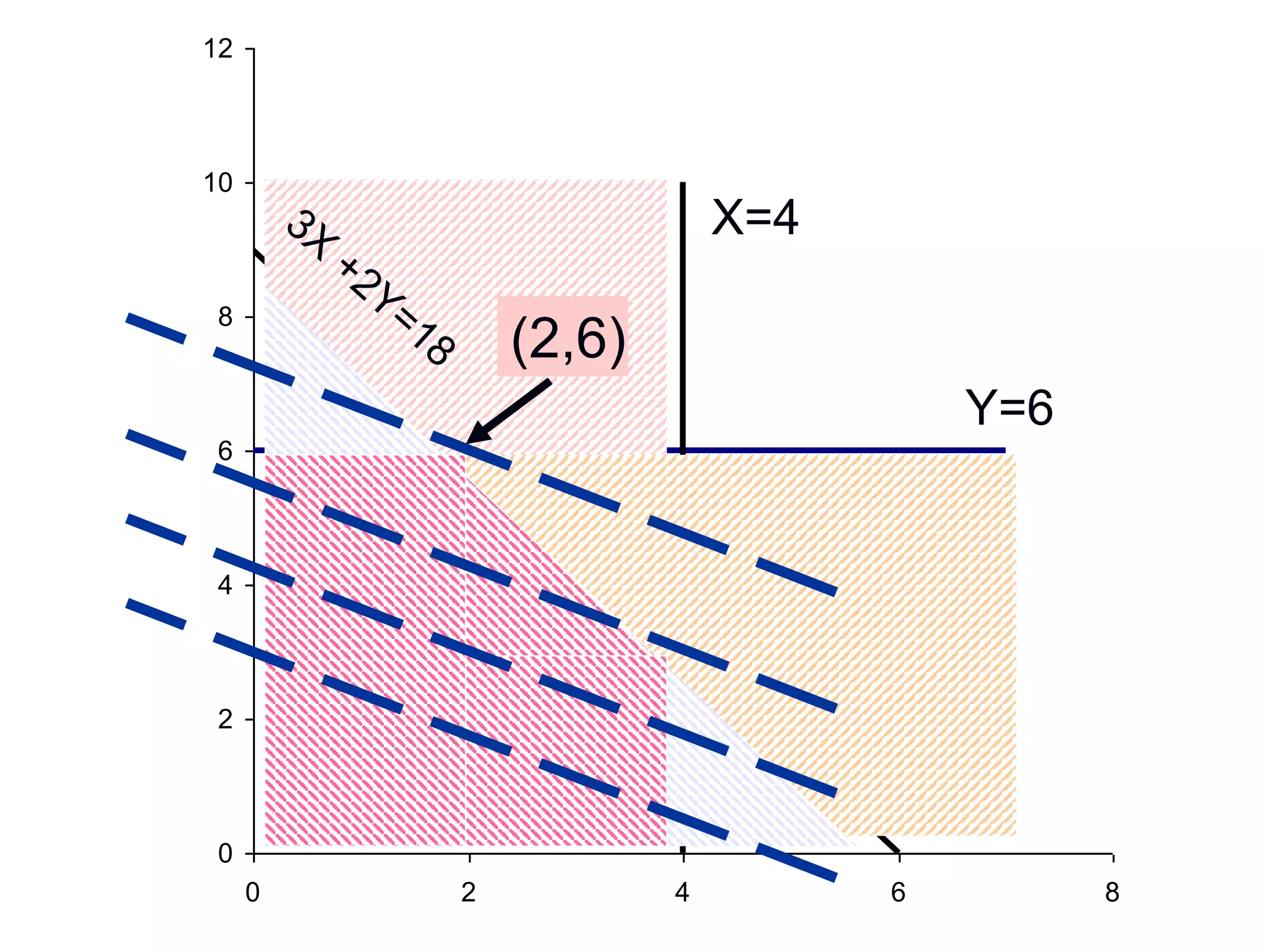
This document discusses operations research and linear programming problems. It provides 3 examples of linear programming problems involving the maximization or minimization of objectives subject to various constraints on resources. The examples cover topics like production planning, resource allocation, and diet optimization. Graphical and algebraic methods are presented for solving the 2-variable linear programming problems. Homework questions involving additional linear programming formulations are provided at the end.