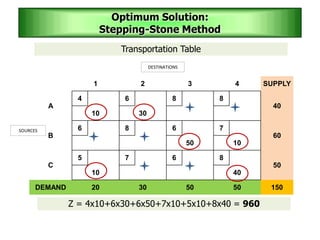
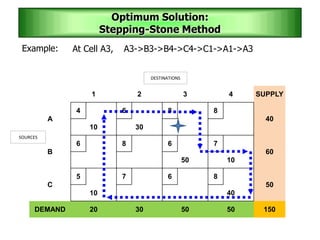
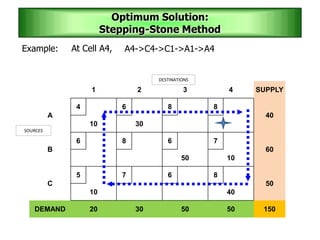
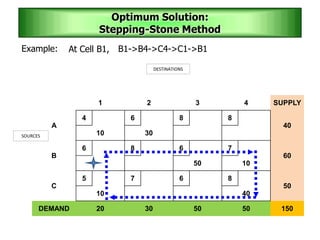
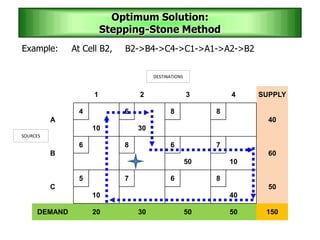
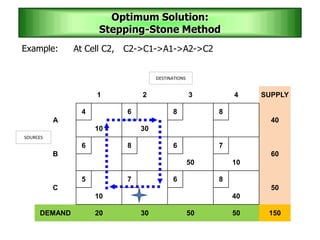
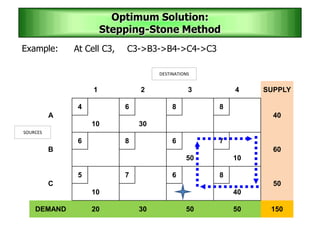
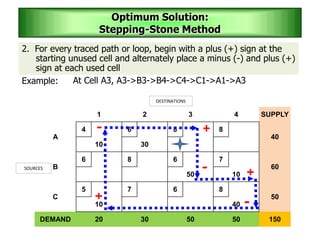
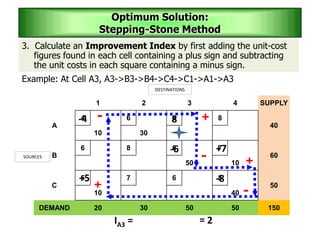
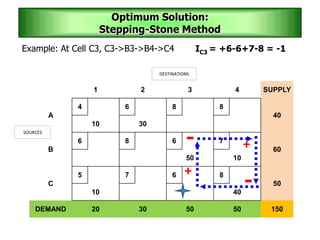
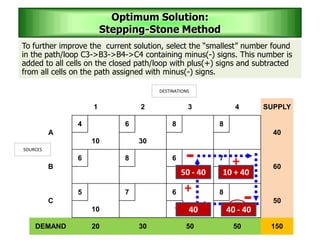
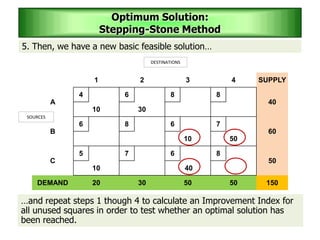
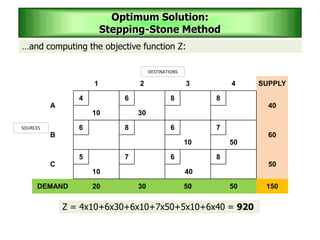
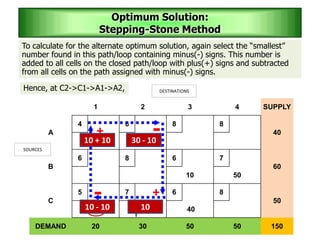
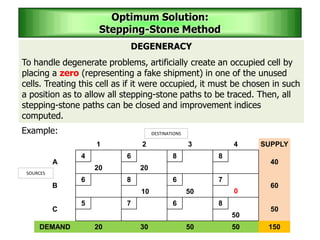
The stepping stone method is used to determine an optimal solution to a transportation problem. It involves tracing closed paths or loops through occupied cells in the transportation table, and calculating improvement indices to test for optimality. The method gets its name from the analogy of crossing a pond by stepping on stones. It involves iteratively improving a feasible solution until all improvement indices are greater than or equal to zero, indicating an optimal solution has been reached.

1. Transportation Problem
- Stepping Stone Method -
PAMANTASAN NG LUNGSOD NG MAYNILA
GRADUATE SCHOOL OF ENGINEERING
GEM 805 – OPTIMIZATION TECHNIQUES

2. Stepping Stone Method
>>> This is a one of the methods used to determine optimality of
an initial basic feasible solution (i.e. Northwest Corner Rule, Least
Cost or Vogel’s Approximation)
>>> The method is derived from the analogy of crossing a pond
using stepping stones. This means that the entire transportation
table is assumed to be a pond and the occupied cells are the
stones needed to make certain movements within the pond.

3. Optimum Solution:
Stepping-Stone Method
1 2 3 4 SUPPLY
A
4 6 8 8
40
10 30
B
6 8 6 7
60
50 10
C
5 7 6 8
50
10 40
DEMAND 20 30 50 50 150
SOURCES
DESTINATIONS
Z = 4x10+6x30+6x50+7x10+5x10+8x40 = 960
Transportation Table

4. 1. Starting at an unused/empty cell, trace a closed path or loop back
to the original cell via cells that are currently being used and/or
occupied.
Note: A closed path or loop is a sequence of cells in the
transportation table such that the first cell is unused/empty
and all the other cells are used/occupied with the following
conditions:
a. Each pair of consecutive used/occupied cells lies in either the
same row or column
b. No three consecutive used/occupied cells lie in the same row
or column
c. The first and last cells of a sequence lies in the same row or
column
d. No cell appears more than once in a sequence (i.e. no
duplication)
e. Only horizontal and vertical moves allowed and can only
change directions at used/occupied cells
Optimum Solution:
Stepping-Stone Method

5. Example:
1 2 3 4 SUPPLY
A
4 6 8 8
40
10 30
B
6 8 6 7
60
50 10
C
5 7 6 8
50
10 40
DEMAND 20 30 50 50 150
SOURCES
DESTINATIONS
Optimum Solution:
Stepping-Stone Method
A3->B3->B4->C4->C1->A1->A3At Cell A3,

6. Example:
1 2 3 4 SUPPLY
A
4 6 8 8
40
10 30
B
6 8 6 7
60
50 10
C
5 7 6 8
50
10 40
DEMAND 20 30 50 50 150
SOURCES
DESTINATIONS
Optimum Solution:
Stepping-Stone Method
At Cell A4, A4->C4->C1->A1->A4

7. 1 2 3 4 SUPPLY
A
4 6 8 8
40
10 30
B
6 8 6 7
60
50 10
C
5 7 6 8
50
10 40
DEMAND 20 30 50 50 150
Optimum Solution:
Stepping-Stone Method
B1->B4->C4->C1->B1
SOURCES
DESTINATIONS
Example: At Cell B1,

8. Example:
1 2 3 4 SUPPLY
A
4 6 8 8
40
10 30
B
6 8 6 7
60
50 10
C
5 7 6 8
50
10 40
DEMAND 20 30 50 50 150
SOURCES
DESTINATIONS
Optimum Solution:
Stepping-Stone Method
At Cell B2, B2->B4->C4->C1->A1->A2->B2

9. Example:
1 2 3 4 SUPPLY
A
4 6 8 8
40
10 30
B
6 8 6 7
60
50 10
C
5 7 6 8
50
10 40
DEMAND 20 30 50 50 150
SOURCES
DESTINATIONS
Optimum Solution:
Stepping-Stone Method
At Cell C2, C2->C1->A1->A2->C2

10. Example:
1 2 3 4 SUPPLY
A
4 6 8 8
40
10 30
B
6 8 6 7
60
50 10
C
5 7 6 8
50
10 40
DEMAND 20 30 50 50 150
SOURCES
DESTINATIONS
Optimum Solution:
Stepping-Stone Method
At Cell C3, C3->B3->B4->C4->C3

11. 2. For every traced path or loop, begin with a plus (+) sign at the
starting unused cell and alternately place a minus (-) and plus (+)
sign at each used cell
1 2 3 4 SUPPLY
A
4 6 8 8
40
10 30
B
6 8 6 7
60
50 10
C
5 7 6 8
50
10 40
DEMAND 20 30 50 50 150
SOURCES
DESTINATIONS
-
-
-
+
+
+
Example:
Optimum Solution:
Stepping-Stone Method
At Cell A3, A3->B3->B4->C4->C1->A1->A3

12. 3. Calculate an Improvement Index by first adding the unit-cost
figures found in each cell containing a plus sign and subtracting
the unit costs in each square containing a minus sign.
1 2 3 4 SUPPLY
A
4 6 8 8
40
10 30
B
6 8 6 7
60
50 10
C
5 7 6 8
50
10 40
DEMAND 20 30 50 50 150
SOURCES
DESTINATIONS
-
-
-
+
+
+
Example: At Cell A3, A3->B3->B4->C4->C1->A1->A3
Optimum Solution:
Stepping-Stone Method
IA3 = 2
-8
-6 +7
+5
-4
=
8

13. Optimum Solution:
Stepping-Stone Method
Iteration #1 - Computing for the Improvement Index:
At A3, A3->B3->B4->C4->C1->A1; IA3 = +8-6+7-8+5-4 = 2
At A4, A4->C4->C1->A1; IA4 = +8-8+5-4 = 1
At B1, B1->B4->C4->C1; IB1 = +6-7-8-5 = 2
At B2, B2->B4->C4->C1->A1->A2; IB2 = +8-7+8-5+4-6 = 2
At C2, Loop C2->C1->A1->A2; IC2 = +7-5+4-6 = 0
At C3, C3->B3->B4->C4; IC3 = +6-6+7-8 = -1
4. If all indices calculated are greater than or equal to zero, then,
an optimal solution had been reached. If not, select the
path/loop that has the most negative value and use this to
further improve the solution.
Note: Should there be two or more “most” negative values,
select arbitrarily.

14. Example: At Cell C3, C3->B3->B4->C4
1 2 3 4 SUPPLY
A
4 6 8 8
40
10 30
B
6 8 6 7
60
50 10
C
5 7 6 8
50
10 40
DEMAND 20 30 50 50 150
SOURCES
DESTINATIONS
Optimum Solution:
Stepping-Stone Method
+
+
-
-
IC3 = +6-6+7-8 = -1

15. To further improve the current solution, select the “smallest” number found
in the path/loop C3->B3->B4->C4 containing minus(-) signs. This number is
added to all cells on the closed path/loop with plus(+) signs and subtracted
from all cells on the path assigned with minus(-) signs.
Optimum Solution:
Stepping-Stone Method
1 2 3 4 SUPPLY
A
4 6 8 8
40
10 30
B
6 8 6 7
60
50 10
C
5 7 6 8
50
10 40
DEMAND 20 30 50 50 150
SOURCES
DESTINATIONS
+
+
-
-
40
50 - 40 10 + 40
40 - 40

16. 5. Then, we have a new basic feasible solution…
1 2 3 4 SUPPLY
A
4 6 8 8
40
10 30
B
6 8 6 7
60
10 50
C
5 7 6 8
50
10 40
DEMAND 20 30 50 50 150
SOURCES
DESTINATIONS
Optimum Solution:
Stepping-Stone Method
…and repeat steps 1 though 4 to calculate an Improvement Index for
all unused squares in order to test whether an optimal solution has
been reached.

17. Optimum Solution:
Stepping-Stone Method
Iteration #2 - Computing for the Improvement Index:
At A3, A3->C3->C1->A1; IA3 = +8-6+5-4 = 3
At A4, A4->B4->B3->C3->C1->A1; IA4 = +8-7+6-6+5-4 = 2
At B1, B1->B3->C3->C1; IB1 = +6-6+6-5 = 1
At B2, B2->B3->C3->C1->A1->A2; IB2 = +8-6+6-5+4-6 = 1
At C2, C2->C1->A1->A2; IC2 = +7-5+4-6 = 0
At C4, C3->B3->B4; IC3 = +8-6+6-7 = 1
Since the results of all indices calculated are greater than or equal to
zero, then, an optimal solution had been reached.

18. …and computing the objective function Z:
1 2 3 4 SUPPLY
A
4 6 8 8
40
10 30
B
6 8 6 7
60
10 50
C
5 7 6 8
50
10 40
DEMAND 20 30 50 50 150
SOURCES
DESTINATIONS
Optimum Solution:
Stepping-Stone Method
Z = 4x10+6x30+6x10+7x50+5x10+6x40 = 920

19. In Iteration #2 :
At A3, A3->C3->C1->A1; IA3 = +8-6+5-4 = 3
At A4, A4->B4->B3->C3->C1->A1; IA4 = +8-7+6-6+5-4 = 2
At B1, B1->B3->C3->C1; IB1 = +6-6+6-5 = 1
At B2, B2->B3->C3->C1->A1->A2; IB2 = +8-6+6-5+4-6 = 1
At C2, C2->C1->A1->A2; IC2 = +7-5+4-6 = 0
At C4, C3->B3->B4; IC3 = +8-6+6-7 = 1
Optimum Solution:
Stepping-Stone Method
However, in checking the calculation in Iteration #2, there is an
improvement index equal to zero. This means that there is an
ALTERNATE optimum solution:

20. To calculate for the alternate optimum solution, again select the “smallest”
number found in this path/loop containing minus(-) signs. This number is
added to all cells on the closed path/loop with plus(+) signs and subtracted
from all cells on the path assigned with minus(-) signs.
Optimum Solution:
Stepping-Stone Method
1 2 3 4 SUPPLY
A
4 6 8 8
40
10 30
B
6 8 6 7
60
10 50
C
5 7 6 8
50
10 40
DEMAND 20 30 50 50 150
SOURCES
DESTINATIONS
+
+ -
- 10
30 - 1010 + 10
10 - 10
Hence, at C2->C1->A1->A2,

21. Then the alternate optimum solution with objective function Z:
1 2 3 4 SUPPLY
A
4 6 8 8
40
20 20
B
6 8 6 7
60
10 50
C
5 7 6 8
50
10 40
DEMAND 20 30 50 50 150
SOURCES
DESTINATIONS
Optimum Solution:
Stepping-Stone Method
Z = 4x20+6x20+6x10+7x50+7x10+6x40 = 920

22. 1 2 3 4 SUPPLY
A
4 6 8 8
40
20 20
B
6 8 6 7
60
10 50
C
5 7 6 8
50
50
DEMAND 20 30 50 50 150
SOURCES
DESTINATIONS
When the number of empty/occupied cells in any solution (either
initial or later) of the transportation table is not equal to the number
of rows plus the number of columns minus 1 (i.e. m+n-1) the
solution is called DEGENERATE
Optimum Solution:
Stepping-Stone Method
Example: m + n -1 = 3 + 4 -1 = 6
DEGENERACY

23. DEGENERACY
To handle degenerate problems, artificially create an occupied cell by
placing a zero (representing a fake shipment) in one of the unused
cells. Treating this cell as if it were occupied, it must be chosen in such
a position as to allow all stepping-stone paths to be traced. Then, all
stepping-stone paths can be closed and improvement indices
computed.
Optimum Solution:
Stepping-Stone Method
1 2 3 4 SUPPLY
A
4 6 8 8
40
20 20
B
6 8 6 7
60
10 50
C
5 7 6 8
50
50
DEMAND 20 30 50 50 150
SOURCES
0
Example: DESTINATIONS

24. QUESTIONS?
Optimum Solution:
Stepping-Stone Method

25. DIOS MABALOS PO!
Cam on !
Shukriya !
ありがとうございます！
Thank you!
Merci!
Gracias!
Obrigado!
謝謝！