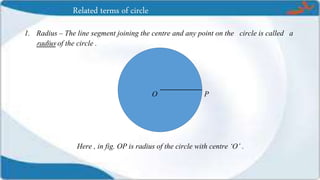
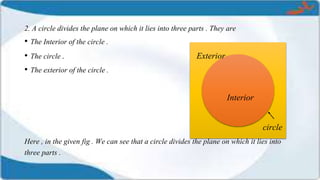
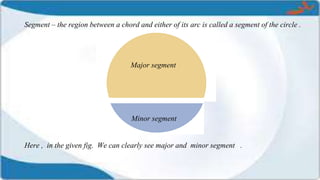
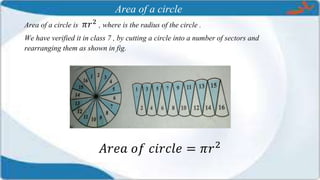
This presentation covers the concepts of circles, including their definitions, related terms, and calculations for perimeter and area. It explains the distinctions between sectors and segments, and provides formulas for calculating the areas of circles, semicircles, and associated plane figures. Key points include the properties of chords, diameters, arcs, and sectors, along with their respective calculations.

1. CIRCLES
Made by :- Amit choube
Class :- 10th ‘ B ’

2. Introduction
In this power point presentation we will discuss about
• Circle and its related terms .
• Concepts of perimeter and area of a circle .
• Finding the areas of two special parts of a circular region known as sector and segment .
• Finding the areas of some combinations of plane figures involving circles or their parts .

3. Contents
 Circle and its related terms .
 Area of a circle .
Areas related to circle .
 Perimeter of a circle .
 Sector of a circle and its area .
 Segment of a circle and its area
 Areas of combinations of plane figures .

4. Circle – Definition
The collection of all the points in a plane which
are at a fixed distance from in the plane is
called a circle .
or
A circle is a locus of a point which moves in a
plane in such a way that its distance from a
fixed point always remains same.

5. 1. Radius – The line segment joining the centre and any point on the circle is called a
radius of the circle .
O P
Here , in fig. OP is radius of the circle with centre ‘O’ .
Related terms of circle

6. 2. A circle divides the plane on which it lies into three parts . They are
• The Interior of the circle .
• The circle . Exterior
• The exterior of the circle .
Interior
circle
Here , in the given fig . We can see that a circle divides the plane on which it lies into
three parts .

7. 3. Chord – if you take two points P and Q on a circle , then the line segment PQ is called a chord of
the circle .
4. Diameter – the chord which passes through the centre of the circle is called a diameter of the circle
.
O
P R
Here in the given fig. OR is the diameter of the circle and PR is the chord of the circle .
Note :- A diameter of a circle is the longest chord of the circle .

8. 1. Arc – the piece of circle between two points is called an arc of the circle .
Q .
Major Arc PQR
P . . R
Minor Arc PR
Here in the given fig. PQR is the major arc because it is the longer one whereas PR is the minor arc of the given
circle . When P and Q are ends of a diameter , then both arcs are equal and each is called a semicircle

9. Segment – the region between a chord and either of its arc is called a segment of the circle .
Major segment
Minor segment
Here , in the given fig. We can clearly see major and minor segment .

10. Sector – the region between two radii , joining the centre to the end points of the arc is called a
sector .
A
B
Here in the given fig. you find that minor arc corresponds to minor sector and major arc
correspondence to major sector .

11. Perimeter of a circle
• The distanced covered by travelling around a circle is its perimeter , usually called its circumference
.
We know that circumference of a circle bears a constant ratio with its diameter .
→
𝑐𝑖𝑟𝑐𝑢𝑚𝑓𝑒𝑟𝑒𝑛𝑐𝑒
𝑑𝑖𝑎𝑚𝑒𝑡𝑒𝑟
= 𝜋
→ 𝑐𝑖𝑟𝑢𝑚𝑓𝑒𝑟𝑒𝑛𝑐𝑒 = 𝜋 × 𝑑𝑖𝑎𝑚𝑒𝑡𝑒𝑟
→ 𝑐𝑖𝑟𝑐𝑢𝑚𝑓𝑒𝑟𝑒𝑛𝑐𝑒 = 𝜋 × 2𝑟 (diameter = 2r)
→ 𝑐𝑖𝑟𝑐𝑢𝑚𝑓𝑒𝑟𝑒𝑛𝑐𝑒 = 2𝜋r

12. Area of a circle
Area of a circle is 𝜋𝑟2 , where is the radius of the circle .
We have verified it in class 7 , by cutting a circle into a number of sectors and
rearranging them as shown in fig.
𝐴𝑟𝑒𝑎 𝑜𝑓 𝑐𝑖𝑟𝑐𝑙𝑒 = 𝜋𝑟2

13. Area and circumference of semicircle
Area of circle = 𝜋𝑟2
Area of semi – circle =
1
2
(Area of circle)
Area of semicircle =
1
2
𝜋𝑟2
and
Perimeter of circle = 2𝜋𝑟
Perimeter of semi circle =
1
2
𝑃𝑒𝑟𝑖𝑚𝑒𝑡𝑒𝑟 𝑜𝑓 𝑐𝑖𝑟𝑐𝑙𝑒 + 𝑑𝑖𝑎𝑚𝑒𝑡𝑒𝑟
Perimeter of semi circle = 𝜋𝑟 +2𝑟 = 𝜋 + 2 𝑟

14. Area of a sector .
Following are some important points to remember
1. A minor sector has an angle 𝜃 , (say) , subtended at the centre of the circle ,
whereas a major sector has no angle .
2. The sum of arcs of major and minor sectors of a circle is equal to the circumference
of the circle .
3. The sum of the areas of major and minor sectors of a circle is equal to the areas of
the circle .
4. The boundary of a sector consists of an arc of the circle and the two radii .

15. If an arc subtends an angle of 180° at the centre , then its arc length is 𝜋r .
If the arc subtends an angle of θ at the centre , then its arc length is
→ 𝑙 =
𝜃
180
× 𝜋𝑟
→ 𝑙 =
𝜃
360
× 2𝜋𝑟
If the arc subtends an angle θ , then the area of the corresponding sector is
→
𝜋𝑟2 𝜃
360
=
𝜃
180
×
1
2
𝜋𝑟2
Thus the area A of a sector of angle θ then area of the corresponding sector is
→ 𝐴 =
𝜃
360
× 𝜋𝑟2
Now, → 𝐴 =
1
2
𝜃
180
× 𝜋𝑟 𝑟
→ 𝐴 =
1
2
𝑙𝑟
Area of a sector.

16. Area of a sector.

17. Some useful results to remember .
1. Angle described by one minute hand in 60 minute =360 ͦ
→ Angle described by minute hand in one minute =
360
60
= 6
Thus , minute hand rotates through an angle of 6 in one minute .
2. Angle described by hour hand in 12 hours = 360 ͦ
→ Angle described hour hand in one minute =
360
12
= 30
Thus , hour hand rotates through 30 ͦ in one minute .

18. Area of a segment of a circle

19. Thank you