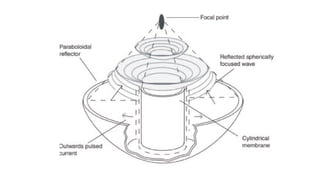
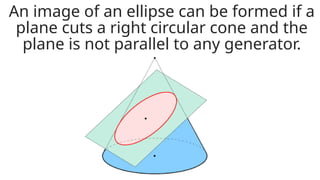
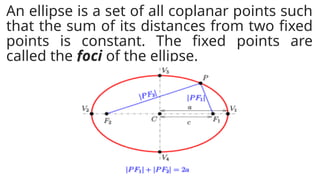
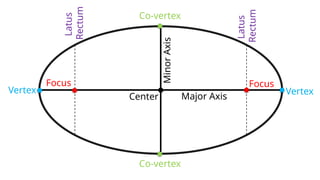
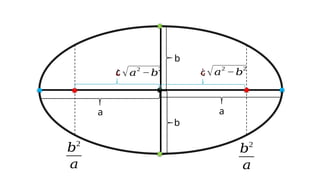
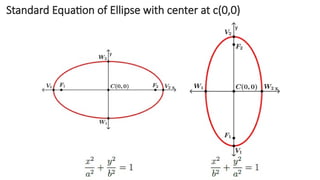
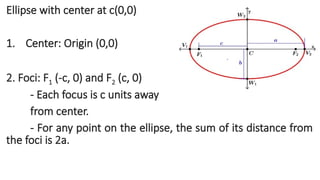
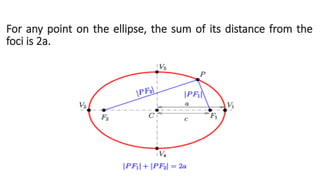
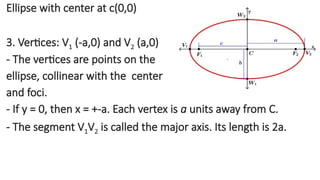
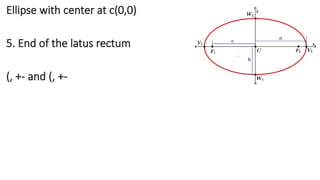
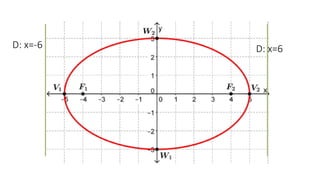
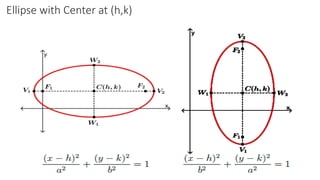
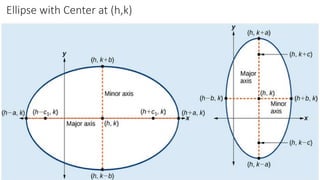
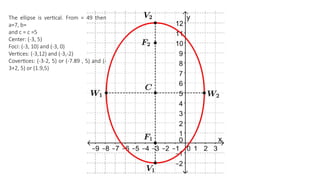
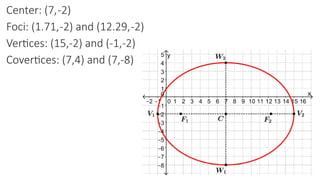
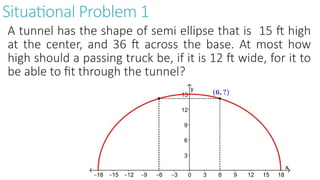
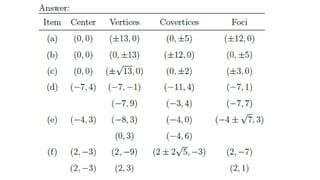
The document details the definition, properties, and equations of ellipses, including standard forms, axes of symmetry, and key coordinates such as foci, vertices, and covertices. It provides examples of situational problems involving elliptical shapes in architecture and mechanics, and includes exercises and quizzes for practice. Additionally, the document explains how to graph ellipses and determine their equations based on given conditions.

1. Ellipse

2. Objectives:
•Define an ellipse.
•Determine the standard form of
equation of an ellipse.
•Graph an ellipse in a rectangular
coordinate system
•Solve situational problems.

4. Elliptical Roads

5. Architectural
Designs

6. Logo
Designs

7. Medical
Equipment
LITHOTRIPTER

10. An ellipse is a closed figure in a plane that
closely resembles an oval.

11. An image of an ellipse can be formed if a
plane cuts a right circular cone and the
plane is not parallel to any generator.

12. An ellipse is a set of all coplanar points such
that the sum of its distances from two fixed
points is constant. The fixed points are
called the foci of the ellipse.

13. Parts of an Ellipse:
An ellipse has two axes of symmetry. The longer axis is called
the major axis, and the shorter axis is called the minor axis.
The major axis contain the foci which are inside of the ellipse.

14. Center
Co-vertex
Co-vertex
Vertex Vertex
Focus
Focus
Latus
Rectum
Latus
Rectum
Minor
Axis
Major Axis

15. a a
b
b
c c
𝑏2
𝑎
𝑏2
𝑎
¿ √𝑎
2
−𝑏
2
¿ √𝑎
2
−𝑏
2

16. Standard Equation of Ellipse with center at c(0,0)

17. Ellipse with center at c(0,0)
1. Center: Origin (0,0)
2. Foci: F1 (-c, 0) and F2 (c, 0)
- Each focus is c units away
from center.
- For any point on the ellipse, the sum of its distance from
the foci is 2a.

18. For any point on the ellipse, the sum of its distance from the
foci is 2a.

19. Ellipse with center at c(0,0)
3. Vertices: V1 (-a,0) and V2 (a,0)
- The vertices are points on the
ellipse, collinear with the center
and foci.
- If y = 0, then x = +-a. Each vertex is a units away from C.
- The segment V1V2 is called the major axis. Its length is 2a.

20. Ellipse with center at c(0,0)
4. Covertices: W1 (0,-b) and W2 (0,b)
-The segment through the center,
perpendicular to the major axis is
the minor axis.
-If x=0, then y=+-b. Each covertex is b units away from the
center.
-The minor axis W1W2is 2b units long. Since a > b, the major
axis is longer than the minor axis.

21. Ellipse with center at c(0,0)
5. End of the latus rectum
(, +- and (, +-

22. Example: Give the coordinates of the foci, vertices, covertices
and directrices of the ellipse with equation. Sketch the graph.
Solution:
By inspection on the equation, we can say that the Center is at
(0,0)with horizontal major axis.
Step 1: Find a and b: a=5 Vertices: (-5,0) and (5,0)
b=3 Covertices: (0,-3) and (0,3)
Step 2: Find c: = = 4

23. Example: Give the coordinates of the vertices, covertices, foci
and directrices of the ellipse with equation. Sketch the graph.
Step 2: Find c: = = 4
F: (-4,0) and (4,0)
Step 3: Find the directrices: d = a – c = 5 – 4 = 1
Since line VF is equidistant to VD then
D: x =-6 , x =6

24. D: x=-6 D: x=6

25. Example 2: Find the standard equation of the ellipse whose foci
are F1 (-3,0) and F2 (3,0) such that for any point on it, the sum of
the distances from the foci is 10.
Answer:

26. Seatwork:
1. Give the coordinates of the vertices, covertices, foci and
directrices of the ellipse with the equation. Sketch the
graph.
2. Find the equation in standard form of the ellipse whose foci
are F1 (-8,0) and F2 (8,0), such that for any point on it, the sum
of the distances from foci is 20.

27. Assignment:
Find the coordinates of the foci and directrices, the endpoints
of the major axis, minor axis and the latus rectum for each
ellipse whose center (0,0). Draw the ellipse, its foci and
directrices.

28. Quiz:
Write the equation of the ellipse with center at the origin that
satisfies the given conditions. Draw the ellipse, its foci and
directrices.
a. The foci have coordinates (+-4,0) and a vertex at (5,0).
b. The length of the latus rectum is and the vertices have
coordinates (0,-5) and (0,5).
Hint: (+- or LR = 2

29. Ellipse with Center at (h,k)

30. Ellipse with Center at (h,k)

31. Note that if is the denominator of , the major axis is horizontal.
If is the denominator of the , the major axis is vertical.
The gen form of the equation
Where A>0, C>0 and A≠C. However, there are other cases with
the same general form that are not ellipse. These are
degenerate conics.

32. 10 a
week
300
100
water
125
floorwax
125
floorwax

33. Example: Give the coordinates of the center, foci, vertices and
covertices of the ellipse with the given equation. Sketch the
graph and include these points.
1.
2.

34. Solution1.
The ellipse is vertical. From = 49 then a=7, b=
and c = c =5
Center: (-3, 5)
Foci: (-3, 10) and (-3, 0)
Vertices: (-3,12) and (-3,-2)
Covertices: (-3-2, 5) or (-7.89 , 5) and (-3+2, 5) or (1.89,5)

35. The ellipse is vertical. From = 49 then
a=7, b=
and c = c =5
Center: (-3, 5)
Foci: (-3, 10) and (-3, 0)
Vertices: (-3,12) and (-3,-2)
Covertices: (-3-2, 5) or (-7.89 , 5) and (-
3+2, 5) or (1.9,5)

36. Solution 2.
We first change the given equation to standard form.
The ellipse is horizontal. From = 64 then a=8, b= b=6,
and c = c = = = 5.3

37. Center: (7,-2)
Foci: (1.71,-2) and (12.29,-2)
Vertices: (15,-2) and (-1,-2)
Covertices: (7,4) and (7,-8)

38. Example 3:
Express each equation in standard form. Determine the center,
foci, vertices, covertices and directrices. Find the length of the
minor axis, major axis and latus rectum.
4

39. Situational Problem 1
A tunnel has the shape of semi ellipse that is 15 ft high
at the center, and 36 ft across the base. At most how
high should a passing truck be, if it is 12 ft wide, for it to
be able to fit through the tunnel?

40. Situational Problem 1
A road tunnel with a semi elliptical arch has 16 m wide
base a 6 m high altitude at the center. How close to the
either wall of the tunnel can a vehicle that is 2 m high
pass by the tunnel?

41. Seatwork:
1. The foci of an ellipse are (-3,-6) and (-3, 2). For any point on
the ellipse, the sum of its distances from the foci is 14. Find
the standard equation of the ellipse.
2. Give the coordinates of the center, foci, vertices and
covertices of the ellipse with equation . Sketch the graph
and include these points.
3. An ellipse has vertices of (-10,-4) and (6,-4) and covertices
(-2,-9) and (-2, 1). Find its standard equation and its foci.

42. Assignment:
Give the coordinates of the center, vertices, covertices, and foci
of the ellipse with the given equation. Write your answers in
table form as below. Sketch the graph, and include these
points.

44. Quiz:
A. Write the equation of the ellipse in standard form that satisfies
the given conditions. Draw the ellipse, its foci and directrices.
1. The foci have coordinates (+-4,0) and a vertex at (5,0).
2. The center is at (7,-2), a vertex at (2,-2) and an endpoint of a
minor axis at (7,-6).
3. The vertices are at (-2, -2) and (-2, 8) and the length of the
minor axis is 6.
4. The center is at (4,3), the length of the horizontal major axis is
5, the length of the minor axis is 4.
5. Foci (-7,6) and (-1,6), the sum of the distances of any point
from the foci is 14.

45. Quiz:
B. Express each equation in standard form. Determine the
center, foci, vertices, covertices, end points of latus rectum and
directrices. Find the length of the minor axis, major axis and
latus rectum.

46. Quiz:
C. The arch of a bridge is in the shape of semi ellipse, with its
major axis at the water level. Suppose the arch is 20 ft high in
the middle, and 120 ft across its major axis. How high above
the water level is the arch, at a point 20 ft from the center
(horizontally)?

47. Thank you and God bless!