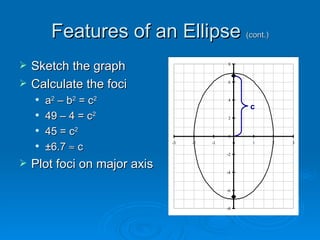
The document discusses the basic equations and features of ellipses. It explains that the center, major axis, minor axis, vertices and foci of an ellipse can be determined from its standard equation. It provides an example of developing the equation of an ellipse given its center, vertices and co-vertices. The major axis is determined by the larger denominator a and the minor axis by the smaller denominator b.

1. Algebra II Equations of Ellipses

2. Basic Equations Center is at ( h , k ) Remember to change signs Major axis is determined by a Always the larger denominator Association with x or y determines direction Length is 2 a or | a | units each direction from the center The points on the major axis are vertices

3. Basic Equations (cont.) Minor axis is determined by b Perpendicular to major axis Length is 2 b or | b | units each direction from the center The points on the minor axis are CO-vertices

4. Basic Equations (cont.) Foci are |c| units each direction from the center on the major axis Foci are determined by the equation above

5. Features of an Ellipse Include sketch of graph for all! Put in standard form by dividing to get “=1”

6. Features of an Ellipse (cont.) Since nothing is with the x or y h = 0 k = 0 the center is at the origin

7. Features of an Ellipse (cont.) larger denominator determines the equation larger denominator is always a 2 a 2 = 49 a = ±7 a is with y  major axis is in y -direction b = ±2

8. Features of an Ellipse (cont.) major axis is in y -direction Measure a = ±7 from center in y -direction Measure b = ±2 from center in x -direction b a

9. Features of an Ellipse (cont.) Sketch the graph Calculate the foci a 2 – b 2 = c 2 49 – 4 = c 2 45 = c 2 ±6.7  c Plot foci on major axis c

10. Developing Equation for Ellipse Center (0, 0) Co-vertex (0, 4) Vertex (10, 0) Must be two vertices  also (–10, 0) Point is on x -axis means this is the major axis Determines which formula to use a must be with the x

11. Developing Equation for Ellipse (cont) Vertex (10, 0) & (–10, 0) a is distance from center to vertex a = 10 a 2 = 100 Co-vertex (0, 4) & (0, -4) b is distance from center to co-vertex b = 4 b 2 = 16

12. Developing Equation for Ellipse (cont) Center (0, 0) h = 0 k = 0 Plug-in a 2 & b 2 a 2 = 100 b 2 = 16

13. Developing Equation for Ellipse (cont) For problems giving focus Use: a 2 – b 2 = c 2 to solve for the missing value Remember the focus is c