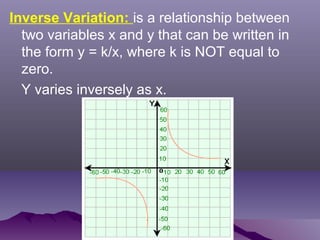
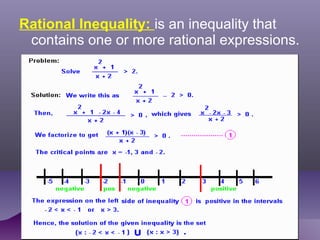
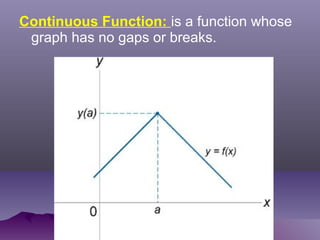
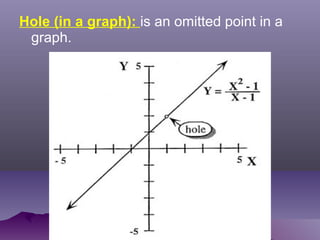
This document lists and defines vocabulary words from math lessons on various topics: - Direct, inverse, joint, and combined variation define relationships between variables that can be written as equations involving a constant of variation. - Rational expressions are quotients of polynomials. Complex fractions contain fractions in the numerator and/or denominator. - Rational functions are functions whose rules can be written as a ratio of two polynomials. These may be continuous or discontinuous. 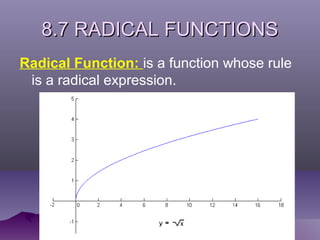- Radical expressions involve a variable within a radical, or root. Rational exponents are exponents that can be expressed as a ratio of integers. 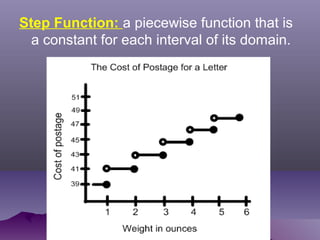- Piecewise functions combine one or more functions over different intervals. Step functions are constant over each interval.

1. Vocabulary Words fromVocabulary Words from
Lessons 8.1 - 8.8 and 9.2 -Lessons 8.1 - 8.8 and 9.2 -
9.49.4

2. 8.1 DIRECT VARIATION8.1 DIRECT VARIATION
Direct Variation: is a relationship between
two variables x and y that can be written in
the form y = kx, where k is NOT equal to
zero.
Y varies directly as x.

3. Constant of Variation: in a direct
variation relationship, k is the constant of
variation.

4. Joint Variation: is the relationship among
three variables that can be written in the
form y = kxz, where k is the constant of
variation.
Y varies jointly as x and z.
For example:
Variable M varies jointly as the values of p and q.
If M = 88 when p = 4 and q = .4,
find M when p = 8 and q = 1.2.

5. Inverse Variation: is a relationship between
two variables x and y that can be written in
the form y = k/x, where k is NOT equal to
zero.
Y varies inversely as x.

6. Combined Variation: is a relationship that
contains both direct and inverse variation.
For example:
If y varies directly as x and inversely as z, and y = 24 when x = 48
and z = 4, find x when y = 44 and z = 6.

7. 8.2 MULTIPLYING AND DIVIDING8.2 MULTIPLYING AND DIVIDING
RATOINAL EXPRESSIONSRATOINAL EXPRESSIONS
Rational Expression: is a quotient of two
polynomials.

8. 8.3 ADDING AND SUBTRACTING8.3 ADDING AND SUBTRACTING
RATIONAL EXPRESSIONSRATIONAL EXPRESSIONS
Complex Fraction: contains one or more
fractions in its numerator, its denominator,
or both.

9. 8.4 RATIONAL FUNCTIONS8.4 RATIONAL FUNCTIONS
Rational Function: is a function whose rule
can be written as a ratio of two
polynomials.

10. Discontinuous Function: is a function
whose graph has one or more gaps or
breaks.

11. Continuous Function: is a function whose
graph has no gaps or breaks.

12. Hole (in a graph): is an omitted point in a
graph.

13. 8.5 SOLVING RATIONAL EQUATIONS8.5 SOLVING RATIONAL EQUATIONS
AND INEQUALITIESAND INEQUALITIES
Rational Equation: is an equation that
contains one or more rational expressions.

14. Extraneous Solution: is a solution of an
equation derived from an original equation
that is not a solution of the original
equation.

15. Rational Inequality: is an inequality that
contains one or more rational expressions.

16. 8.6 RADICAL EXPRESSIONS AND8.6 RADICAL EXPRESSIONS AND
RATIONAL EXPONENTSRATIONAL EXPONENTS
Index: the nth root of a real number a can
be written as the radical expression where
n is the index (plural: indices) of the
radical and a is the radicand.

17. Rational Exponent: is an exponent that can
be expressed as m/n, where m and n are
integers and is n is NOT equal to zero.

18. 8.7 RADICAL FUNCTIONS8.7 RADICAL FUNCTIONS
Radical Function: is a function whose rule
is a radical expression.

19. Square-Root Function: is a radical function
involving

20. 8.8 SOLVING RADICAL EQUATIONS8.8 SOLVING RADICAL EQUATIONS
AND INEQUALITIESAND INEQUALITIES
Radical Equation: contains a variable
within a radical.

21. Radical Inequality: is an inequality that
contains a variable within a radical.

22. 9.2 PIECEWISE FUNCTION9.2 PIECEWISE FUNCTION
Piecewise Function: is a function that is a
combination of one or more functions.

23. Step Function: a piecewise function that is
a constant for each interval of its domain.

24. 9.3 TRANSFORMING9.3 TRANSFORMING
FUNCTIONSFUNCTIONS
There are no vocabulary words for this
lesson.

25. 9.4 OPERATIONS WITH9.4 OPERATIONS WITH
FUNCTIONSFUNCTIONS
Composition of Functions: a function
operation that uses the output from one
function as the input for a second
function.