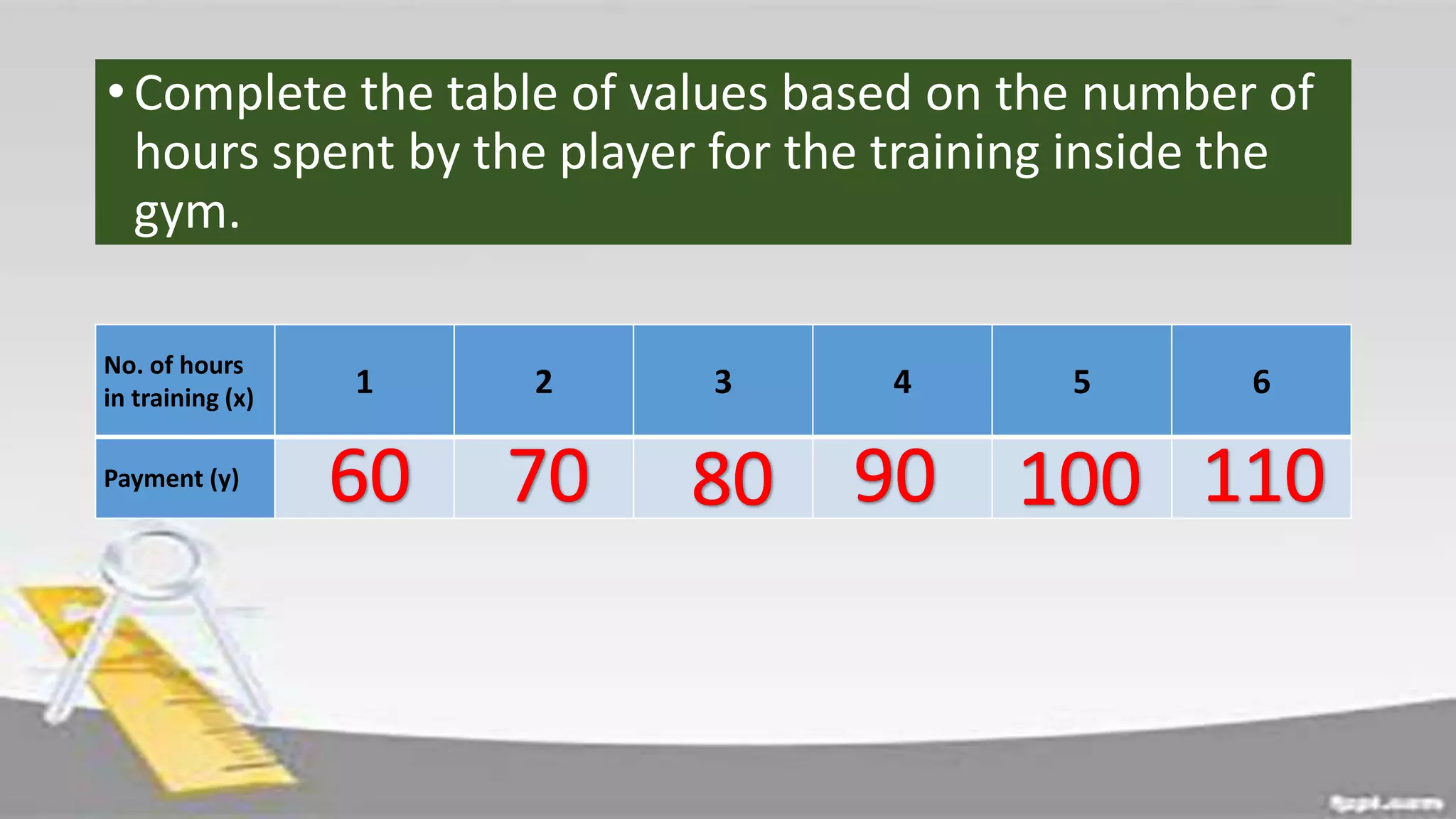
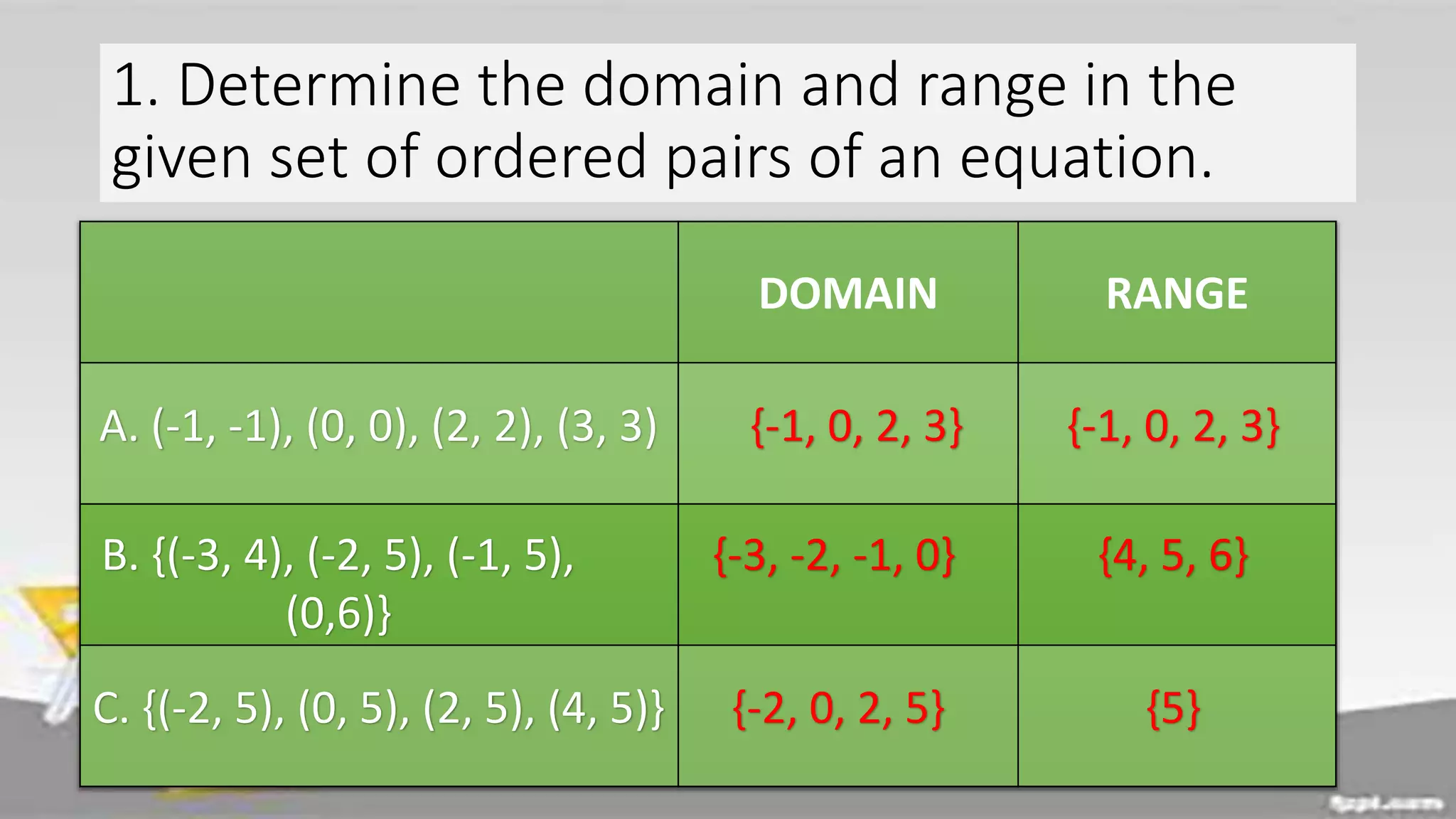
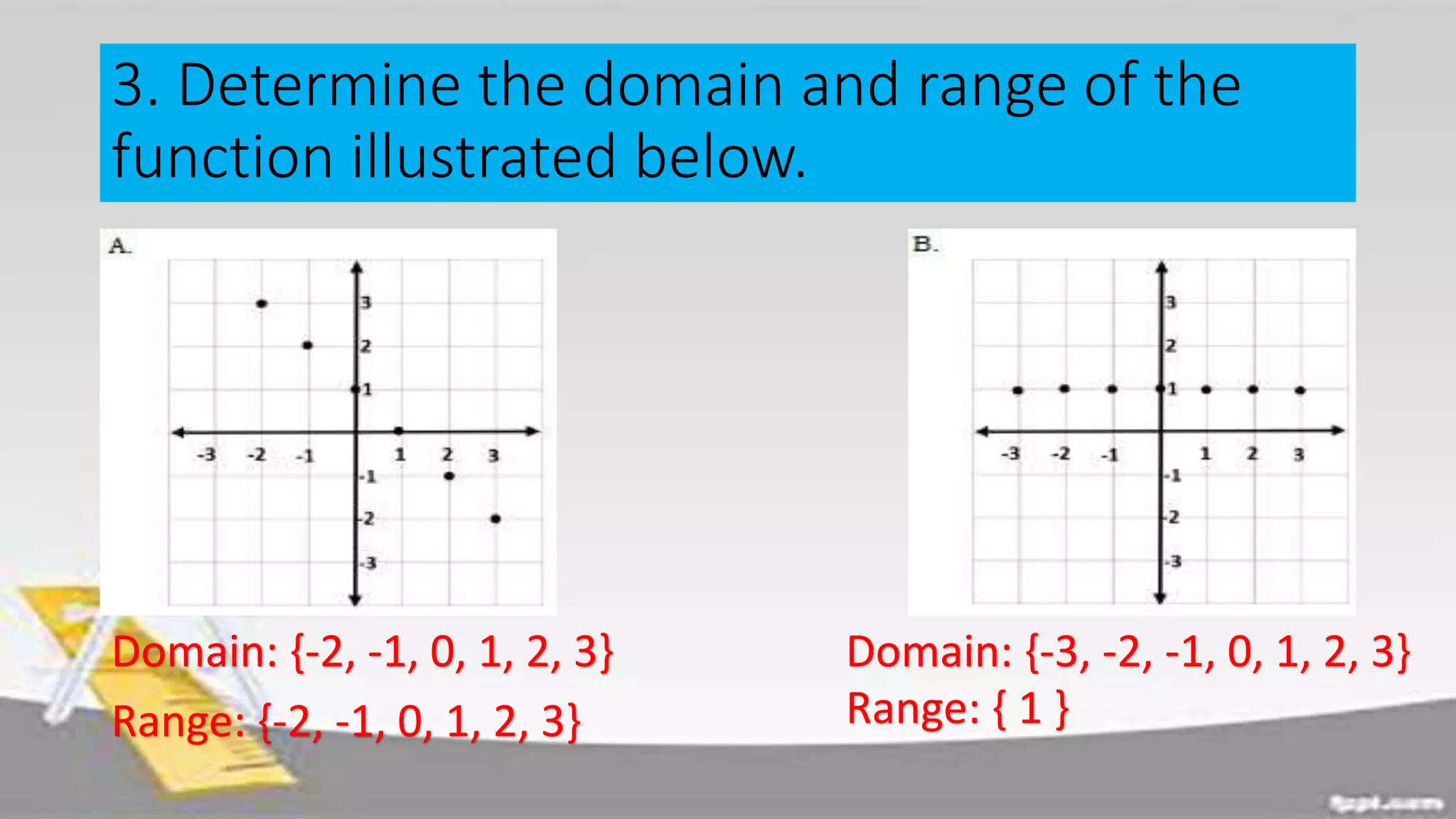
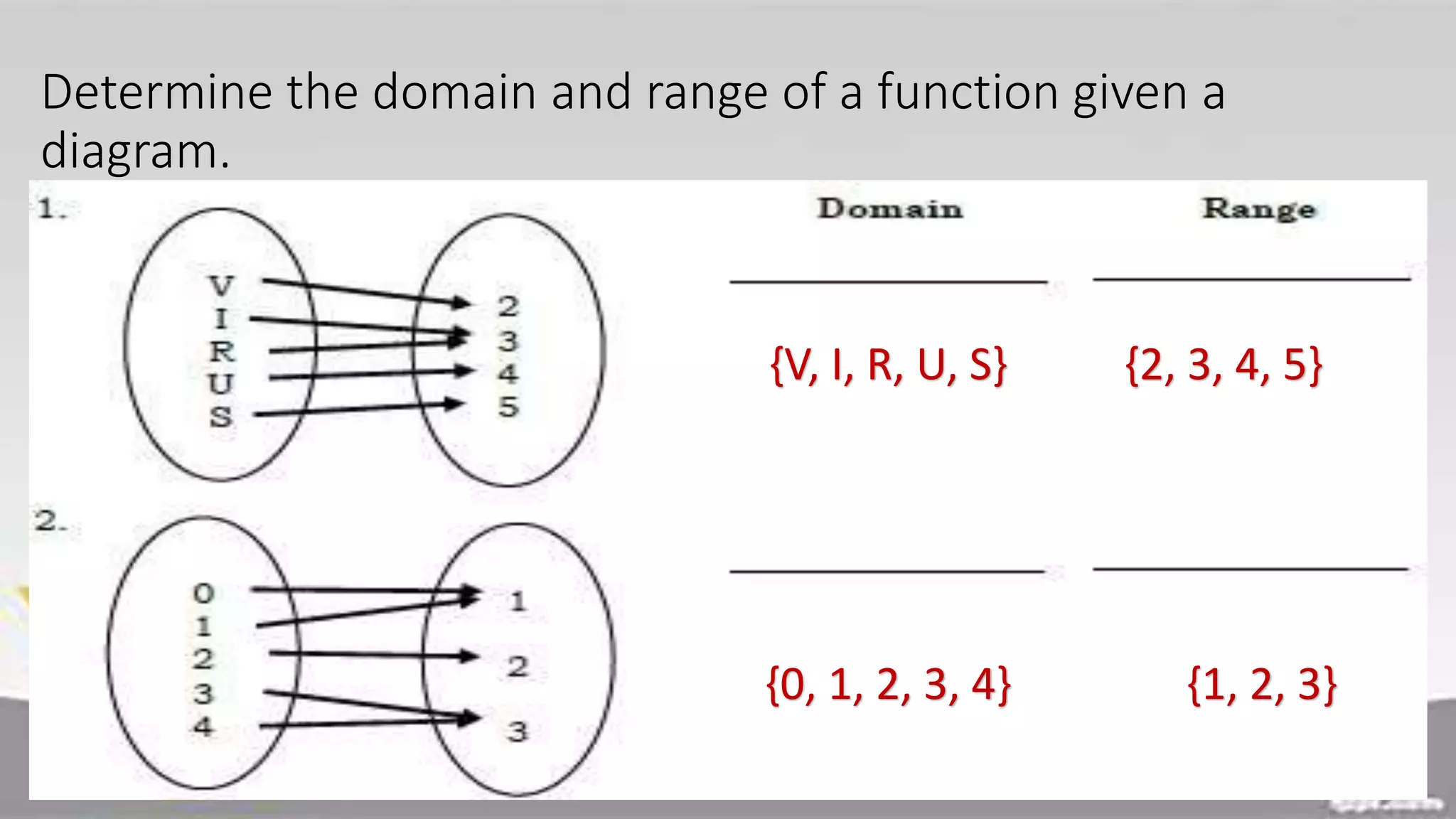
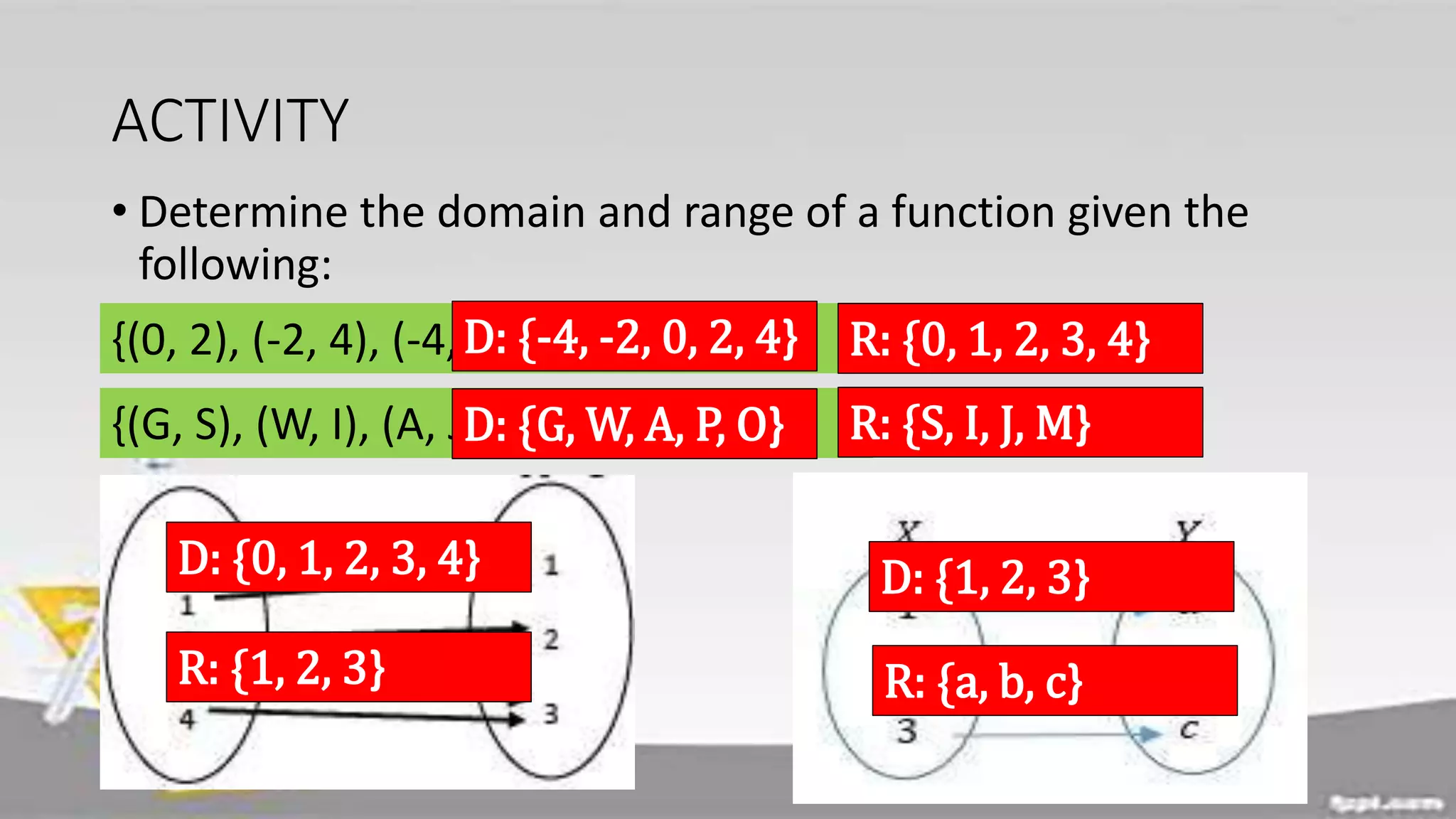
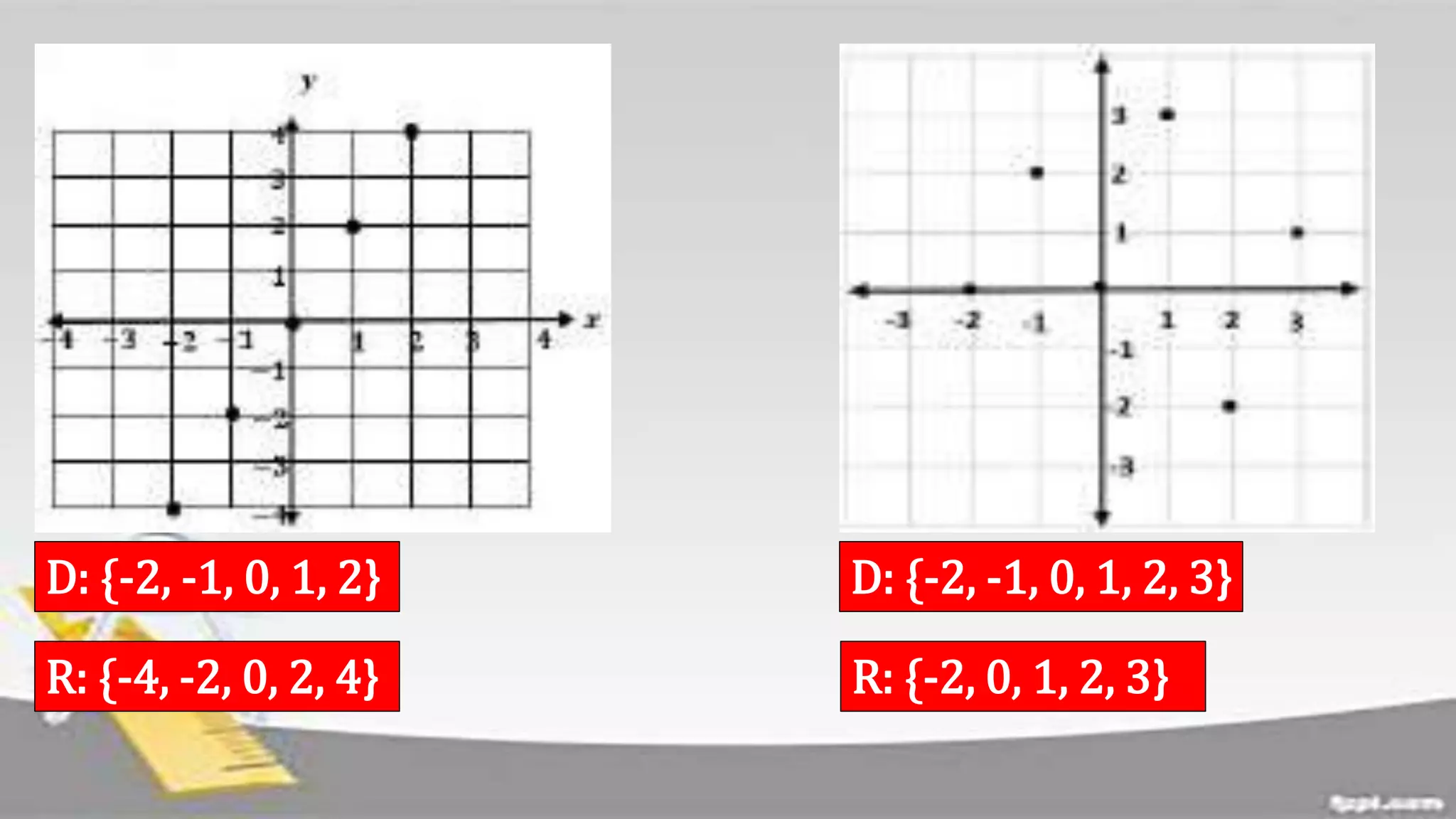
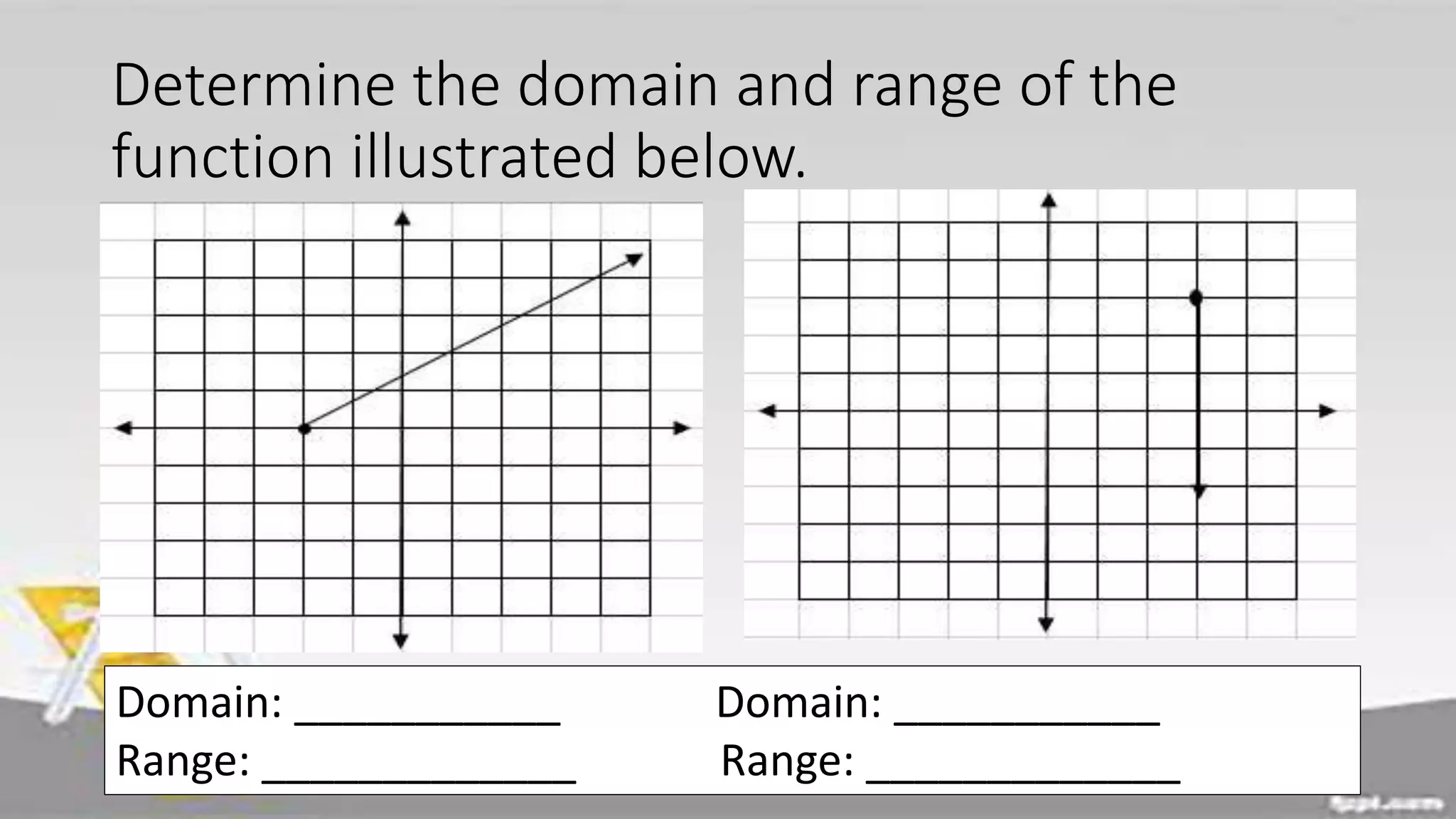
The document discusses domain and range of functions. It defines domain as the set of all first coordinates (x-values) of ordered pairs in a function, and range as the set of all second coordinates (y-values). Examples are provided to demonstrate determining the domain and range from ordered pairs, graphs, and equations defining functions. Key aspects like the domain and range being all real numbers for linear functions are covered. Activities have learners practice finding domains and ranges in various scenarios.

1. Dependent Variable
- Represents a quantity whose value depends on how
the independent variable is manipulated.
- A variable that does not depend on any other variable
for its value.
Independent Variable
How long you sleep affects your test score.

2. Activity 1: What’s Your Order?
• A school canteen sells lunch for P45. To facilitate the payments and
avoid inaccuracy in computations, the student manager prepared a
table to which she can refer when receiving payments. A part of the
table is shown below.
No. of Sudents
(x) 1 2 3 4 5 6 7 8
Amount paid
(y) 45 90 135 180 225 270 315 360
1. How much will four students spend for lunch?
2. Do you see the pattern? State the rule that describe the pattern.

3. Domain and Range
Of a Function
(M8AL- IId-1)

4. Objectives
* Find the domain and range of a function given an ordered
pair.
* Find the domain and range of a function given a graph.
* Find the domain and range of a function given an equation.

5. Activity 2: Training Day
• In preparation for the Palarong Pambansa 2020, a badminton
player decided to use a gym for his practice. He pays an initial
amount of P50 plus P10 for every hour of use. Relate the total
amount paid to the number of hours spent inside the gym.
• What mathematical equation represents the problem?
• How much will the player pay if he decided to practice
for six hours?

6. •Complete the table of values based on the number of
hours spent by the player for the training inside the
gym.
No. of hours
in training (x) 1 2 3 4 5 6
Payment (y)

7. •How to find domain and range of a function?
Example:
{(1, 2), (2, 3), (3, 4), (4, 5)}
Domain: {1, 2, 3, 4}
Range: {2, 3, 4, 5}

8. FUNCTION
- A function from X into Y is a rule or a correspondence that
associates with each element of X a unique element of Y.
DOMAIN
- the set of all the first coordinates of the ordered pairs in a
function or the x values.
RANGE
- the set of all the second coordinates of the ordered pairs in a
function or the y values.

9. 1. Determine the domain and range in the
given set of ordered pairs of an equation.
DOMAIN RANGE
A. (-1, -1), (0, 0), (2, 2), (3, 3)
B. {(-3, 4), (-2, 5), (-1, 5),
(0,6)}
C. {(-2, 5), (0, 5), (2, 5), (4, 5)}
{-1, 0, 2, 3} {-1, 0, 2, 3}
{-3, -2, -1, 0} {4, 5, 6}
{-2, 0, 2, 5} {5}

10. 2. Consider the correspondence shown in each diagram
below.
Range: {Sampaguita, Rose, Santan}
Domain: {Chris, Alvin, Marichu, Joey}
Range: {27°C, 30°C, 33°C, 29°C, 28°C}
Domain: {6AM, 8AM, 12PM, 2PM, 5PM, 9PM}
Domain: {-2, 0, 1, 2}
Range: {-5, -1, 0, 6}

11. 3. Determine the domain and range of the
function illustrated below.
Domain: {-2, -1, 0, 1, 2, 3}
Range: {-2, -1, 0, 1, 2, 3} Range: { 1 }
Domain: {-3, -2, -1, 0, 1, 2, 3}

12. Domain: {x ≤ 0} since 0 is the highest
x value and the arrow indicates the
line continues to the left. It includes
zero since the dot is solid.
Range: {y ≥ 0} since 0 is the lowest y
value and the arrow indicates the line
continues upward. It includes zero
since the dot is solid.

13. If the function f is defined by (𝑥) = 𝑚𝑥 + 𝑏, where
𝑚 ≠ 0, then the domain and range of the function
is the set of all real numbers.
In symbols,
• 𝐷𝑓 = {x │x € R}, read as: “the domain of the function f is the
set of all x such that x is an element of the set of real
numbers,”
• 𝑅𝑓 = {y │y € R}, read as: “the range of the function f is the set
of all y such that y is an element of the set of real numbers.”

14. 4. Determine the domain and range of a function
given an equation.
A. Find the domain and range of the function f(x) = x + 6.
𝐷𝑓 = {𝑥│𝑥 € 𝑅} 𝑅𝑓 = {𝑦|𝑦 € 𝑅}
B. Find the domain and range of the function 𝑓 𝑥 =
2𝑥
𝑥+2
.
𝐷𝑓 = {𝑥│𝑥 € 𝑅, x ≠ -2} 𝑅𝑓 = {𝑦|𝑦 € 𝑅, y ≠ 2}

15. Determine the domain and range of a
function given an ordered pairs.
Domain Range
1. (2, 5), (3, 10), (4, 16), (5, 24) ___________ ____________
2. (-4, 10), (-3, 5), (-1, 7), (9, 11) ___________ ____________
3. (L, M), (O, A), (V, T), (E, H) ___________ ____________
{2, 3, 4, 5} {5, 10, 16, 24}
{-4, -3, -1, 9} {5, 7, 10, 11 }
{L, O, V, E} {M, A, T, H}

16. Determine the domain and range of a function given a
diagram.
{V, I, R, U, S} {2, 3, 4, 5}
{0, 1, 2, 3, 4} {1, 2, 3}

17. ACTIVITY
• Determine the domain and range of a function given the
following:
{(0, 2), (-2, 4), (-4, 0), (4, 1), (2, 3)}
{(G, S), (W, I), (A, J), (P, M), (O, M)}
D: {-4, -2, 0, 2, 4} R: {0, 1, 2, 3, 4}
D: {G, W, A, P, O} R: {S, I, J, M}
D: {0, 1, 2, 3, 4}
R: {1, 2, 3}
D: {1, 2, 3}
R: {a, b, c}

18. D: {-2, -1, 0, 1, 2}
R: {-4, -2, 0, 2, 4}
D: {-2, -1, 0, 1, 2, 3}
R: {-2, 0, 1, 2, 3}

19. APPLICATION
• Herson pays an amount of P12 per hour for using the
internet. During Saturdays and Sundays, he enjoys and
spends most of his time playing a game especially if he is
with his online friends. He plays the game for almost 4 hours.
How much will Herson pay for using the internet for 1 hour? 2
hours? 3 hours? 4 hours?
Express each as an ordered pair.
Based on your answers on items number 2, what is the
domain? What is the range?
12
24 36 48
{(1, 12), (2, 24), (3, 36), (4, 48)}
Domain: {1, 2, 3, 4}
Range: {12, 24, 36, 48}

20. Generalization
• Domain is the set of input values, while range is the
set of output values. To determine the domain and
range of any function on a graph, the general idea is
to assume that they are both real numbers, then look
for places where no values exist.

21. Determine the domain and range of the
function illustrated below.
Domain: ___________ Domain: ___________
Range: _____________ Range: _____________

22. THANK YOU   