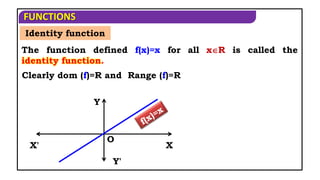
The document provides an overview of various mathematical functions, including constant, identity, modulus, reciprocal, signum, square root, greatest integer, fractional part, exponential, logarithmic, polynomial, and rational functions. It details their definitions, domains, and ranges, along with important properties and rules for determining the domain and range of functions. Additionally, the document summarizes standard functions and their respective domains and ranges.

1. FUNCTIONS
FUNCTIONS

2. FUNCTIONS
SOME IMPORTANT
FUNCTIONS

3. FUNCTIONS
Then, the
function defined by f(x)=c for all xR
SOME IMPORTANT FUNCTIONS
Constant function: Let ‘c’ be the fixed number.
is called a constant
function.
Clearly, domain of (f)=R and Range of (f)={c}
X' X
Y
Y'
f(x)=c
(0, c)
O

4. FUNCTIONS
Identity function
Clearly dom (f)=R and Range (f)=R
X' X
Y'
Y
O
The function defined f(x)=x for all xR is called the
identity function.

5. FUNCTIONS
Modulus function
X' X
Y'
Y
O
f(x)=
x, when x0
-x, when x<0
is called Modulus function.
The function is defined by,

6. FUNCTIONS
We have dom (f)=R and range (f)=[0, )
Remarks:
1. x = max {x, -x} (for all xR)
2. −x = x
3. x±y ≤ x + y

7. FUNCTIONS
Reciprocal function
Y'
X' X
Y
O
dom(f)=R-{0}
Clearly, x is not defined when y=0
Range (f)=R-{0}
Clearly,
1
x
is not defined when x=0
Also, y=
1
x
 x=
1
y
The function defined by f(x)=
1
x
is called the reciprocal
function.
Can you guess the
domain of f in this
case?

8. FUNCTIONS
Signum function
f(x) =
x
x
when x  0
0, when x = 0
Clearly f(x)=
1, when x > 0
0, when x = 0
-1, when x < 0
is called the signum function.
The function defined by

9. FUNCTIONS
O
X' X
Y'
Y
f(x)=1
f(x)=-1
-1
1
Domain (f)=R and range (f)={-1,0,1}

10. FUNCTIONS
Square Root function
The function f(x)=+ x is called the square root function.
Since negative real number do not have real square roots,
therefore domain of (f)=[0,).
Also, range (f)=[0, ).
X' X
Y'
Y
O
f(x)=+ x

11. FUNCTIONS
Greatest Integer Function or Step Function
We have domain of (f)=R and range of (f)=Z
X' X
Y'
Y
O
Thus f(x)=n if nx<n+1 (nZ)
The function f(x)=[x] defined as the greatest integer not
exceeding x, is called the greatest Integer function.

12. FUNCTIONS
Properties of greatest integer function
(i) nx<n+1[x]=n where nZ
(ii) x-1<[x]x<[x]+1
(iii) m [x]nmx<n+1 where m,nZ
(iv) [x+n]=[x]+n, (where n  Z)
(v) [x]+[-x]=
0, when x  Z
-1, when x  Z

13. FUNCTIONS
Where {x}= fractional part of x
(vi) [x+y]=
[x]+[y] (when {x}+{y}<1
[x]+[y]+1 (when {x}+{y}1
(vii) [x]=x iff xz
(viii) x[x] for all x  R

14. FUNCTIONS
Fractional Part Function
X' X
Y'
Y
O
-1
1
Clearly 0{x}<1
We have domain(f)=R and range of (f)=[0, 1)
The function defined as f(x)={x}=x-[x] is called the fractional
part function.

15. FUNCTIONS
(iii) If x is an integer i.e., x=nZ then {x}=x-[x]=n-[n]=n-n=0
(v) f(x)={x} has period 1
(iv) {x}+{-x}=
0, when x  Z
-1, when x  Z
Thus {x}=0 when xZ
Properties of Fractional-Part Function
(i) 0{x}<1
(ii) [{x}]=0

16. FUNCTIONS
Exponential Function
The function f(x)=ex is called exponential function.
In general, if a is a positive real number (a1),
then the exponential function is defined as f(x)=ax
So, domain of (f)=R
Also, y = ax
X' X
Y'
Y
(0, 1)
O
Since f(x)=ex is defined for all xR
Range of (f)=(0,∞)
logy = x log a
log y
log a
= x
x = log a y

17. FUNCTIONS
Clearly, logay is defined only when y is positive
range of (f)=[0, )
X' X
Y'
Y
O
X' X
Y'
Y
(0, 1)
O
(0, 1)

18. FUNCTIONS
then the
logarithmic function is defined as f(x)=logax.
Logarithmic Function
The function f(x)=log x is called the Logarithmic function.
In general, if a is a positive real number (a1)
Since f(x)=logax is defined for all positive real values of x,
so we have Domain of (f)=(0, )

19. FUNCTIONS
Also, y = logax
y =
logx
loga
yloga = logx
logay = logx
x = ay
Clearly, ay defined for all yR

20. FUNCTIONS
X' X
Y'
Y
(1, 0)
O
f(x)=logax, a>1
X' X
Y'
Y
(1, 0)
O
f(x)=logax, 0<a<1
Note
Range of (f)=R
If f(x)=logex  f-1(x)=ex

21. FUNCTIONS
Polynomial Function
A function of the form p(x)=a0xn+a1xn-1+a2xn-2+….an-1x+an,
a0,a1,a2…an are real numbers, a00 and n is a non-negative
integer,is called a polynomial function of degree n.
The domain of a polynomial function is R.
Rational Function
A function of the form f(x)=
p(x)
q x
where p(x) and q(x) are polynomials and q(x)0,
is called a rational function.

22. FUNCTIONS
DOMAIN

23. FUNCTIONS
If f(x)=y is a function, then set of all possible values of x for
which f(x) exists is called as domain of f.
Rules
DOMAIN
(1)
1
f(x)
does not exist
Domain = {xR/f(x)0}=R-{x/f(x)=0}
(2) f(x) exists
Domain = {xR/f(x)0}
when f(x)=0
Do you know the
domain of f(x) in
this case?
when f(x)0

24. FUNCTIONS
(3)
1
f(x)
exists
Domain = {xR /f(x)>0}
(4) log f(x) exists
Domain= {xR/f(x)>0}
(5) log f(x) exists
Domain=R- {x/f(x)=0}
when f(x)>0
when f(x)>0.
when f(x)0

25. FUNCTIONS
(8) D1, D2 are domains of f(x) and g(x).
Then,
(i) Domain of f(x)g(x)
(6)
1
log f(x)
exists
Domain= {x R /f(x) (0,∞)-{1}}
(7) logg(x)f(x) exists
(ii) Domain of f(x)g(x)
(iii) Domain of
f(x)
g(x)
is
when f(x)>0 & f(x) 1
when f(x)>0, g(x)>0 and g(x)1
is D1D2
is D1D2
D1D2-{x/g(x)=0}

26. FUNCTIONS
Important Note: Useful results while calculating domain
are (when <).
x(,)
x[,]
(i) (x-)(x-)<0
(ii) (x-)(x-)0
(iii) (x-)(x-)>0
(iv) (x-)(x-)0
 <x<
 x
 x< or x>
 x or x
x(-∞,)(, ∞)
x(-∞,][, ∞)

27. FUNCTIONS
f(x)=y is a function such that for several values of x, we get
several values to y. Now set of all values of y is called the
range of f.
Rules
RANGE
(1) f(x)=acosx+bsinx+c, then range of f(x) is
[c- a𝟐+b𝟐
,c+ a𝟐+b𝟐
]
(2) If a2+b2+c2=k, then range of ab+bc+ca is
−k
2
,k
(3) While calculating range useful result is AMGMHM

28. FUNCTIONS
Domain and Range of standard functions
S.NO FUNCTION DOMAIN RANGE
1 y=ax xR y(0,∞)
2 y=logex x(0,∞) yR
3 y=[x] xR yZ
4 y= x xR y[0,∞)
5 y= x x[0,∞) y[0,∞)
6 y=Sinx xR y[-1,1]
7 y=Cosx xR y[-1,1]

29. FUNCTIONS
S.NO FUNCTION DOMAIN RANGE
8 y=Tanx xR-{(2n+1)
π
2
;nZ} yR
9 y=Cotx xR-{n;nZ} yR
10 y=Secx xR-{(2n+1)
π
2
;nZ} y(-∞,-1][1,∞)
11 y=Cosecx xR-{n;nZ} y(-∞,-1][1,∞)
12 y=Sin−𝟏x x[-1,1] y −
π
2
,
π
2
13 y=Cos−𝟏
x x[-1,1] y[0,]
14 y=Tan−𝟏
x xR y −
π
2
,
π
2
Domain and Range of standard functions

30. FUNCTIONS
S.NO FUNCTION DOMAIN RANGE
15 y=Cot−1x xR y(0, )
16 y=Sec−1x x(-∞,-1][1,∞) y[0, /2) (/2, ]
17 y=Cosec−1x x(-∞,-1][1,∞) y [-/2,0) (0, /2]
18 y=Sinhx xR yR
19 y=Coshx xR y[1, ∞)
20 y=Tanhx xR y(-1,1)
21 y=Cothx x(-∞,0)(0,∞) y(-∞,-1)(1,∞)
Domain and Range of standard functions

31. FUNCTIONS
S.NO FUNCTION DOMAIN RANGE
22 y=Sechx xR y(0,1]
23 y=Cosechx x(-∞,0)(0,∞) y(-∞,0)(0,∞)
24 y=Sinh−1x xR yR
25 y=Cosh−1x x[1, ∞) y[0,∞)
26 y=Tanh−1x x(-1,1) yR
27 y=Coth−1x x(-∞,-1)(1,∞) y(-∞,0)(0,∞)
28 y=Sech−1x x(0,1] y[0,∞)
29 y=Cosech−1x x(-∞,0)(0,∞) y(-∞,0)(0,∞)
Domain and Range of standard functions

32. FUNCTIONS
1.
1
f(x)
exists when
1) f(x)≥0 2) f(x)>0 3) f(x)<0 4) f(x)≤0
2. log|f(x)|exists when
1) f(x)≠0 2) f(x)>0
3) f(x)<0 4) f(x)≤0

33. FUNCTIONS
3. If (x-)(x-)≤0, which of the following is true
1) <x< 2) x 3) x< or x> 4) x or x
4. f(x)=acosx+bsinx+c then range of f(x) is
1) [c- a𝟐+b𝟐
,c+ a𝟐+b𝟐
]
2) (c- a𝟐+b𝟐
,c+ a𝟐+b𝟐
)
3) (c- a𝟐+b𝟐
,c+ a𝟐+b𝟐
]
4) [c- a𝟐+b𝟐
,c+ a𝟐+b𝟐
)

34. FUNCTIONS
Thank you…