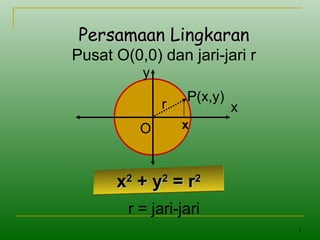
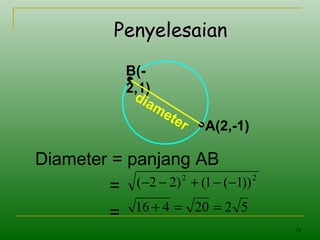
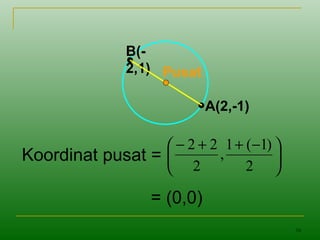
Dokumen tersebut membahas tentang persamaan lingkaran, mulai dari definisi lingkaran sebagai himpunan titik yang berjarak sama dari suatu titik tetap yang disebut pusat, persamaan umum lingkaran dengan pusat di (0,0), contoh soal menentukan persamaan lingkaran berdasarkan pusat dan jari-jari yang diberikan, serta menentukan pusat, jari-jari, dan persamaan lingkaran berdasarkan informasi tambahan seperti mel

1. 1

2. 2
Setelah menyaksikan
tayangan ini anda dapat
Menentukan
persamaan lingkaran
yang memenuhi kriteria tertentu

3. 3
LingkaranLingkaran
tempat kedudukan titik-titik
yang berjarak sama
terhadap suatu titik tetap.
Jarak yang sama itu disebut jari-jari
dan titik tetap itu disebut
pusat lingkaran

4. 4
Persamaan LingkaranPersamaan Lingkaran
Pusat O(0,0) dan jari-jari r
r = jari-jari
x
y
O
r
P(x,y)
x
xx22
+ y+ y22
= r= r22

5. 5
Soal 1
Persamaan lingkaran
pusatnya di O(0,0) dan jari-jari:
a. r = 5 adalah x2
+ y2
= 25
b. r = 2½ adalah x2
+ y2
= 6¼
c. r = 1,1 adalah x2
+ y2
= 1,21
d. r = √3 adalah x2
+ y2
= 3

6. 6
Soal 2
Persamaan lingkaran
pusat O(0,0) dan melalui titik (3,-1)
adalah….

7. 7
PenyelesaianPenyelesaian
Misal persamaan lingkaran yang
berpusat di O(0,0) dan jari-jari r
adalah x2
+ y2
= r2
melalui (3,-1) → 32
+ (-1)2
= r2
r2
= 9 + 1
= 10
Jadi, persamaan lingkarannya
adalah x2
+ y2
= 10

8. 8
Soal 3Soal 3
Pusat dan jari-jari lingkaran:
a. x2
+ y2
= 16 adalah…
jawab: pusat O(0,0) dan r = 4
b. x2
+ y2
= 2¼ adalah…
jawab: pusat O(0,0) dan r = 1½
c. x2
+ y2
= 5 adalah…
jawab: pusat O(0,0) dan r = √5

9. 9
Soal 4Soal 4
Persamaan lingkaran yang sepusat
dengan lingkaran x2
+ y2
= 144
tetapi panjang jari-jarinya setengah
dari panjang jari-jari lingkaran
tersebut adalah….

10. 10
PenyelesaianPenyelesaian
Lingkaran x2
+ y2
= 144
pusatnya O(0,0) dan jari-jarinya
r = √144 = 12 → ½r = 6
Persamaan lingkaran yang
pusatnya O(0,0) dan jari-jarinya
r = 6 adalah x2
+ y2
= 62
x2
+ y2
= 36

11. 11
Soal 5Soal 5
Jika titik (2a, -5) terletak pada
lingkaran x2
+ y2
= 41 maka
nilai a adalah….

12. 12
PenyelesaianPenyelesaian
Titik (2a, -5) terletak pada
lingkaran x2
+ y2
= 41,
berarti (2a)2
+ (-5)2
= 41
4a2
+ 25 = 41
4a2
= 41 – 25 = 16
a2
= 4 → a = 2 atau a = -2

13. 13
Soal 6Soal 6
Persamaan lingkaran yang koordinat
ujung-ujung diameternya A(2,-1)
dan B(-2,1) adalah….

14. 14
PenyelesaianPenyelesaian
Diameter = panjang AB
=
=
A(2,-1)
B(-
2,1)
diameter
22
))1(1()22( −−+−−
5220416 ==+

15. 15
Diameter = panjang AB
= 2√5
Jari-jari = ½ x diameter
= ½ x 2√5
= √5

16. 16
Koordinat pusat =
= (0,0)
A(2,-1)
B(-
2,1) Pusat





 −++−
2
)1(1
,
2
22

17. 17
Jadi,
persamaan lingkarang yang
jari-jari = √5 dan pusat (0,0)
adalah x2
+ y2
= (√5)2
x2
+ y2
= 5

18. 18
(x – a)(x – a)22
+ (y - b)+ (y - b)22
= r= r22
Pusat lingkaran (a,b) , r = jari-jariPusat lingkaran (a,b) , r = jari-jari
a
(a, b)b
(0,0)
Persamaan LingkaranPersamaan Lingkaran
Pusat (a,b) dan jari-jari rPusat (a,b) dan jari-jari r
x
y

19. 19
Soal 1Soal 1
Tentukan pusat dan jari-jari lingkaran
a. (x – 3)2
+ (y – 7)2
= 9
jawab: pusat di (3,7) dan
jari-jari r = √9 = 3
b. (x – 8)2
+ (y + 5)2
= 6
jawab: pusat di (8,-5) dan
jari- jari r = √6

20. 20
Tentukan pusat dan jari-jari lingkaran
c. (x + 3)2
+ (y – 5)2
= 24
jawab: pusat di (-3,5) dan
jari-jari r = √24 = 2√6
d. x2
+ (y + 6)2
= ¼
jawab: pusat di (0,-6) dan
jari- jari r = √¼ = ½

21. 21
Soal 2
Persamaan lingkaran, pusat di (1,5)
dan jari-jarinya 3 adalah ….
Penyelesaian:
(x – a)2
+ (y – b)2
= r2
▪ Pusat (1,5) → a = 1 dan b = 5
▪ Jari-jari r = 3 → r2
= 9
Persamaannya (x – 1)2
+ (y – 5)2
= 9

22. 22
Soal 3
Persamaan lingkaran, pusat di (-1,0)
dan jari-jarinya 3√2 adalah ….
Penyelesaian:
(x – a)2
+ (y – b)2
= r2
▪ Pusat (-1,0) → a = -1 dan b = 0
▪ Jari-jari r = 3√2 → r2
= (3√2)2
= 18
Persamaannya: (x + 1)2
+ y2
= 18

23. 23
Soal 4
Persamaan lingkaran yang
berpusat di titik (-2,-7)
dan melalui titik (10,2) adalah ….

24. 24
P(-2,-7)
A(10,2)
r
Penyelesaian:
Pusat (-2,-7)
→ a = -2, b = -7
Jari-jari = r = AP
AP =
r =
Jadi, persamaan lingkarannya
(x + 2)2
+ (y + 7)2
= 225
22
2)7(10)2( −−+−−
1522581144 ==+ → r2
= 225

25. 25
Soal 5
Persamaan lingkaran yang
berpusat di titik (4,-3)
dan melalui titik pangkal
adalah ….

26. 26
P(4,-3)
O(0,0)
r
Penyelesaian:
Pusat (4,-3)
→ a = 4, b = -3
Jari-jari = r = OP
OP =
r =
Jadi, persamaan lingkarannya
(x - 4)2
+ (y + 3)2
= 25
22
)03()04( −−+−
525916 ==+ → r2
= 25

27. 27
Soal 6
Persamaan lingkaran yang
berpusat di garis x – y = 1,
jari-jari √5 dan
melalui titik pangkal adalah ….

28. 28
Penyelesaian
Misal persamaan lingkarannya
(x – a)2
+ (y – b)2
= r2
▪ melalui O(0,0) → x = 0, y = 0
dan jari-jari r = √5 → r2
= 5
disubstitusi ke (x – a)2
+ (y – b)2
= r2
(0 – a)2
+ (0 – b)2
= 5
a2
+ b2
= 5 …..(1)

29. 29
▪ Pusat (a,b) pada garis x – y = 1
a – b = 1 → a = b + 1 …..(2)
a=b+1 disubstitusi ke a2
+ b2
= 5
(b + 1)2
+ b2
= 5
b2
+ 2b + 1 + b2
= 5
2b2
+ 2b – 4 = 0 → b2
+ b – 2 = 0
(b + 2)(b – 1) = 0
b = -2 atau b = 1

30. 30
▪ b = -2 → a = b + 1 = -2 + 1 = -1
diperoleh pusatnya (-1,-2), r = √5
Jadi, persamaan lingkarannya
(x + 1)2
+ (y + 2)2
= 5
▪ atau b = 1 → a = 1 + 1 = 2
diperoleh pusatnya (2,1), r = √5
Jadi, persamaan lingkarannya
(x – 2)2
+ (y – 1)2
= 5

31. 31
Soal 7
Persamaan lingkaran yang
berpusat pada perpotongan garis
y = x dengan garis x + 2y = 6
melalui titik O(0,0) adalah ….

32. 32
Penyelesaian
▪ pusat pada perpotongan garis
y = x dengan garis x + 2y = 6
substitusi y = x ke x + 2y = 6
x + 2x = 6
3x = 6 → x = 2
x = 2 → y = 2 → pusat (2,2)

33. 33
▪ jari-jari = jarak pusat (2,2) ke O(0,0)
r =
=
Jadi, persamaan lingkarannya
(x – 2)2
+ (y – 2)2
= 8
x2
– 4x + 4 + y2
– 4y + 4 = 8
x2
+ y2
– 4x – 4y = 0 → persamaan
lingkaran dalam bentuk umum
22
)02()02( −+−
844 =+ → r2
= 8

34. 34
xx22
+ y+ y22
+ Ax + By + C = 0+ Ax + By + C = 0
Persamaan LingkaranPersamaan Lingkaran
dalam bentuk umumdalam bentuk umum
Pusat (-Pusat (-½½A, -A, -½½B)B)
r = CBA −−+− 2
2
12
2
1
)()(

35. 35
Soal 1
Tentukan pusat dan jari-jari lingkaran
x2
+ y2
– 2x – 6y – 15 = 0
jawab:
A = -2, B = - 6, C = -15
pusat di (-½A,-½B) → (1, 3)
jari-jari r =
=
)15(31 22
−−+
525 =

36. 36
Soal 2
Tentukan pusat lingkaran
3x2
+ 3y2
– 4x + 6y – 12 = 0
jawab:
3x2
+ 3y2
– 4x + 6y – 12 = 0
x2
+ y2
– x + 2y – 4 = 03
4
Pusat (-½( – ), -½.2)3
4
Pusat( , – 1)3
2

37. 37
Soal 3
Jika titik (-5,k) terletak pada
lingkaran x2
+ y2
+ 2x – 5y – 21 = 0
maka nilai k adalah…

38. 38
Penyelesaian
(-5,k) terletak pada lingkaran
x2
+ y2
+ 2x – 5y – 21 = 0
→ (-5)2
+ k2
+2(-5) – 5k – 21 = 0
25 + k2
– 10 – 5k – 21 = 0
k2
– 5k – 6 = 0
(k – 6)(k + 1) = 0
Jadi, nilai k = 6 atau k = -1

39. 39
Soal 4
Jarak terdekat antara titik (-7,2)
ke lingkaran
x2
+ y2
– 10x – 14y – 151 = 0
sama dengan….

40. 40
PenyelesaianPenyelesaian
Titik T(-7,2) disubstitusi ke
x2
+ y2
– 10x – 14y – 151
(-7)2
+ 22
– 10.(-7) – 14.2 – 151
49 + 4 + 70 – 28 – 151 = - 56 < 0
berarti titik T(-7,2) berada
di dalam lingkaran

41. 41
Pusat x2
+ y2
– 10x – 14y – 151 = 0
adalah P(-½(-10), -½(-14)) = P(5, 7)
QT = PQ - PT
= 15 – 13 = 2
Jadi, jarak terdekat adalah 2
P(5,7)
Q
r
T(-7,2)
)151(75rPQ 22
−−+==
15225 ==r
=PT
13169 ==
22
)72()57( −+−−

42. 42
SELAMAT BELAJAR