Simplilearn, profile picture
Uploaded bySimplilearn
12,004 views

Machine Learning Tutorial Part - 1 | Machine Learning Tutorial For Beginners Part - 1 | Simplilearn

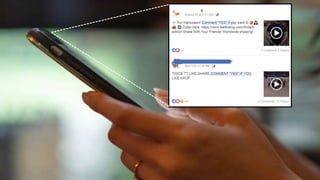
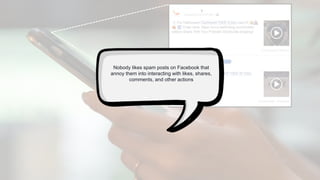
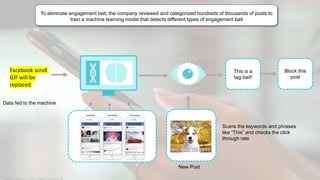
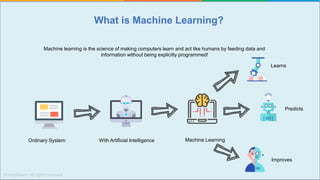
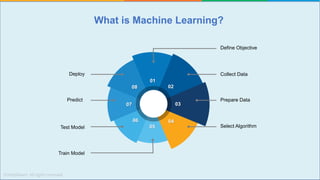
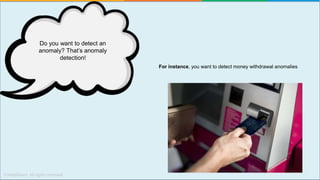
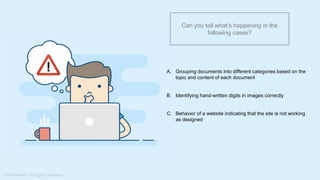
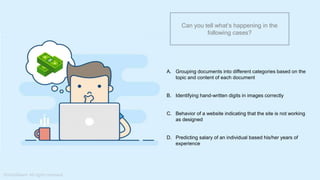
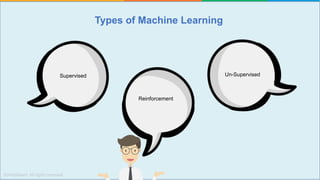
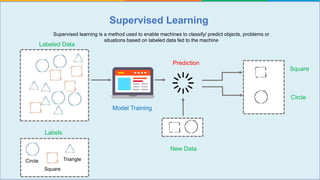
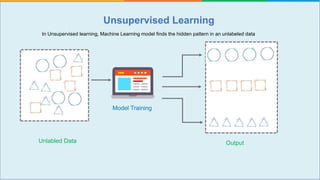
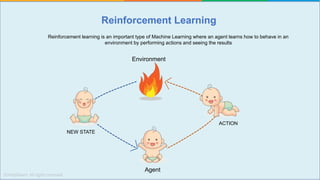
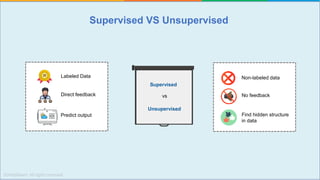
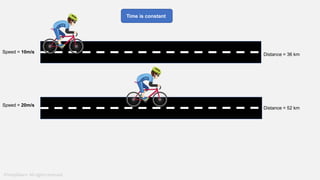
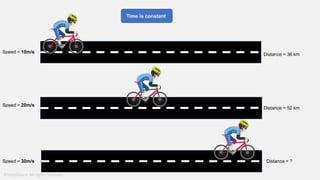
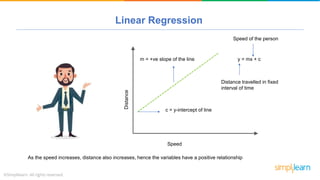
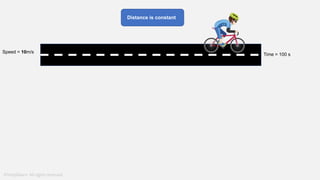
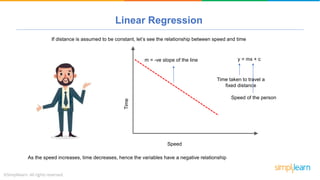
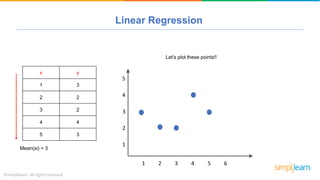
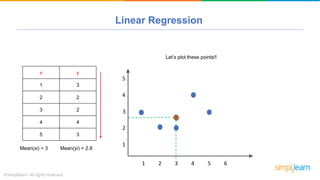
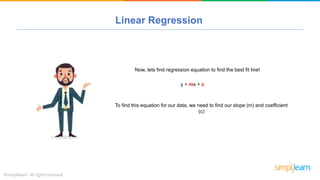
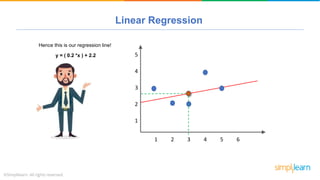
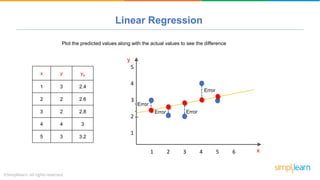
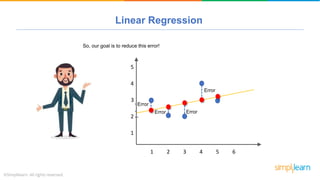
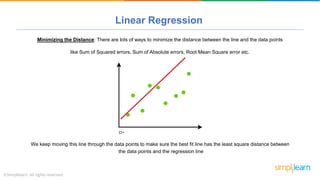
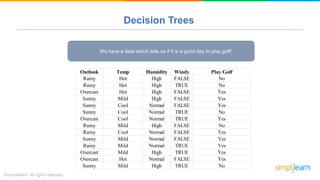
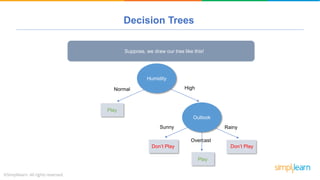
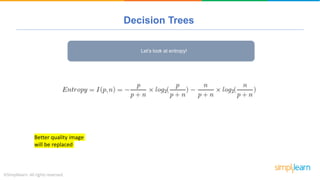
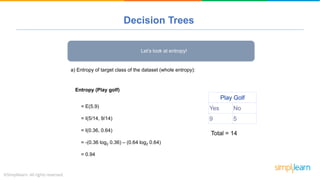
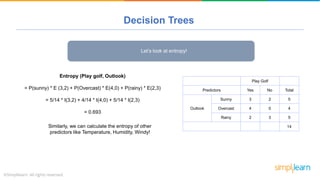
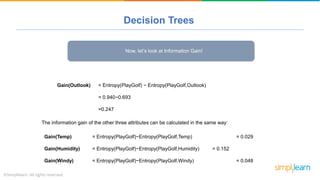
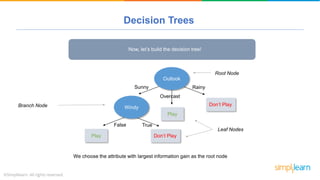
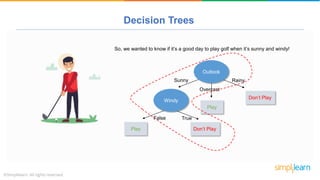
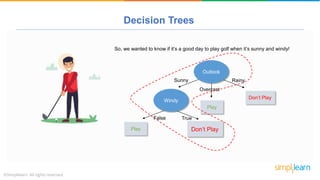
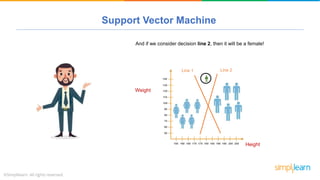
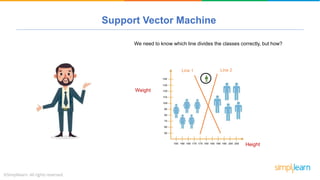
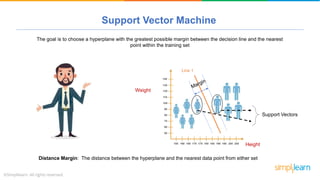
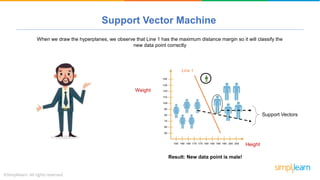
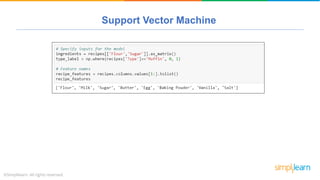
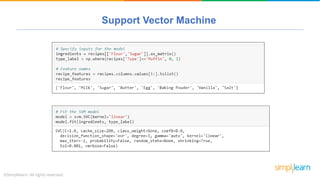
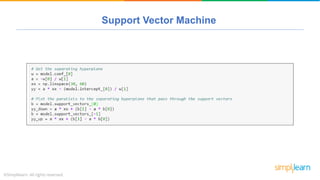
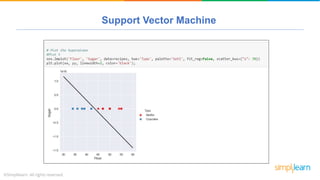
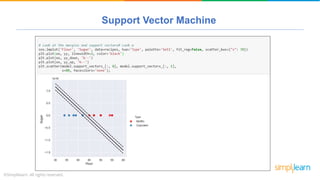
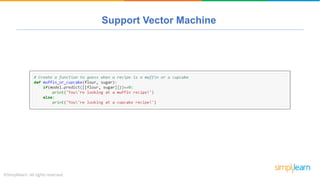
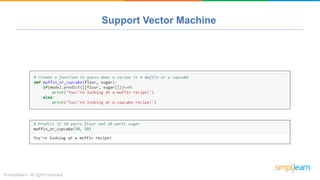
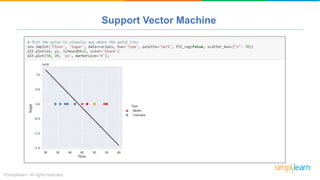
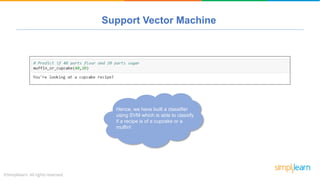
The document provides a comprehensive tutorial on machine learning, covering its definition, types (supervised, unsupervised, and reinforcement learning), and various algorithms (linear regression, decision trees, and support vector machines). It also includes practical use cases, such as classifying recipes and detecting anomalies, along with explanations of key concepts like entropy and information gain in decision trees. Overall, it emphasizes the significance of machine learning in real-world applications and the mechanics behind different learning models.

Embed presentation

Machine learning Tutorial
What’s in it for you? Why Machine Learning? What is Machine Learning? Types Of Machine Learning Machine Learning Algorithms Linear Regression Decision Trees Support Vector Machine Use Case: Classify whether a recipe is of a cupcake or a muffin using SVM
Why Machine Learning? Because Machine can drive your car for you!! Because Machine can unlock your phone with your face!! Because Machine can now detect 50 eye diseases
Why Machine Learning?
Why Machine Learning? Nobody likes spam posts on Facebook that annoy them into interacting with likes, shares, comments, and other actions
Why Machine Learning? This tactic, known as “Engagement Bait,” takes advantage of Facebook’s Newsfeed algorithm by boosting engagement in order to get greater reach
To eliminate engagement bait, the company reviewed and categorized hundreds of thousands of posts to train a machine learning model that detects different types of engagement bait Facebook scroll GIF will be replaced New Post Scans the keywords and phrases like “This” and checks the click through rate This is a tag bait! Block this post Data fed to the machine
Google’s DeepMind project “AlphaGO”, a  computer program that plays the board game ‘GO’ has defeated the world’s number one Go player Ke Jie
What is Machine Learning? Machine learning is the science of making computers learn and act like humans by feeding data and information without being explicitly programmed! Ordinary System With Artificial Intelligence Machine Learning Learns Predicts Improves
Define Objective Collect Data Prepare Data Select Algorithm Deploy Predict Test Model Train Model 01 02 03 04 05 06 07 08 What is Machine Learning?
For instance, whether the stock price will increase or decrease Do you want to predict a category? That’s classification!
For instance, predicting the age of a person based on the height, weight, health and other factors Do you want to predict a quantity? That’s regression!
For instance, you want to detect money withdrawal anomalies Do you want to detect an anomaly? That’s anomaly detection!
For instance: Finding groups of customers with similar behavior given a large database of customer data containing their demographics and past buying records Do you want to discover structure in unexplored data? That’s clustering
What do you understand from Measures and Dimensions? Each field from the data source is automatically assigned a datatype (such as string, integer) and a role (dimension or measure) Aggregation applied on measures is ‘Sum’ by default but you can always change the default aggregation in the settings Can you tell what’s happening in the following cases? A. Grouping documents into different categories based on the topic and content of each document
What do you understand from Measures and Dimensions? Each field from the data source is automatically assigned a datatype (such as string, integer) and a role (dimension or measure) Aggregation applied on measures is ‘Sum’ by default but you can always change the default aggregation in the settings Can you tell what’s happening in the following cases? A. Grouping documents into different categories based on the topic and content of each document B. Identifying hand-written digits in images correctly
What do you understand from Measures and Dimensions? Each field from the data source is automatically assigned a datatype (such as string, integer) and a role (dimension or measure) Aggregation applied on measures is ‘Sum’ by default but you can always change the default aggregation in the settings Can you tell what’s happening in the following cases? A. Grouping documents into different categories based on the topic and content of each document B. Identifying hand-written digits in images correctly C. Behavior of a website indicating that the site is not working as designed
What do you understand from Measures and Dimensions? Each field from the data source is automatically assigned a datatype (such as string, integer) and a role (dimension or measure) Aggregation applied on measures is ‘Sum’ by default but you can always change the default aggregation in the settings Can you tell what’s happening in the following cases? A. Grouping documents into different categories based on the topic and content of each document B. Identifying hand-written digits in images correctly C. Behavior of a website indicating that the site is not working as designed D. Predicting salary of an individual based his/her years of experience
Types of Machine Learning Supervised
Types of Machine Learning Supervised Un-Supervised
Types of Machine Learning Supervised Reinforcement Un-Supervised
Supervised Learning Labeled Data Model Training New Data Square Circle Prediction Supervised learning is a method used to enable machines to classify/ predict objects, problems or situations based on labeled data fed to the machine Circle Square Triangle Labels
Unsupervised Learning Unlabled Data Output In Unsupervised learning, Machine Learning model finds the hidden pattern in an unlabeled data Model Training
Reinforcement Learning Reinforcement learning is an important type of Machine Learning where an agent learns how to behave in an environment by performing actions and seeing the results ACTION NEW STATE Agent Environment
Supervised VS Unsupervised No feedback Find hidden structure in data Supervised vs Unsupervised Labeled Data Direct feedback Predict output Non-labeled data
Support Vector Machine Linear Regression Decision Trees Machine Learning Algorithms There are many interesting Machine Learning algorithms, let’s have a look at a few of them
Linear Regression y = mx + c Linear regression is a linear model, e.g. a model that assumes a linear relationship between the input variables (x) and a single output variable (y) Linear regression is perhaps one of the most well known and well understood algorithms in statistics and machine learning!
Linear Regression Imagine, we are predicting distance travelled (y) from speed (x). Our linear regression model representation for this problem would be: y = m * x + c Or distance = m * speed + c c = coefficient m = y-intercept
Speed = 10m/s Distance = 36 km Time is constant
Speed = 10m/s Distance = 36 km Speed = 20m/s Distance = 52 km Time is constant
Speed = 10m/s Distance = 36 km Speed = 20m/s Distance = 52 km Speed = 30m/s Distance = ? Time is constant
Linear Regression Speed Distance y = mx + c Distance travelled in fixed interval of time c = y-intercept of line m = +ve slope of the line As the speed increases, distance also increases, hence the variables have a positive relationship Speed of the person
Distance is constant Speed = 10m/s Time = 100 s
Speed = 10m/s Time = 100 s Speed = 20m/s Time = 50 s Distance is constant
Speed = 10m/s Time = 100 s Speed = 20m/s Time = 50 s Speed = 30m/s Time = ? Distance is constant
Linear Regression Speed Time y = mx + c Time taken to travel a fixed distance m = -ve slope of the line As the speed increases, time decreases, hence the variables have a negative relationship If distance is assumed to be constant, let’s see the relationship between speed and time Speed of the person
Linear Regression Let’s see the mathematical implementation of Linear Regression! Suppose we have a dataset that looks like: x y 1 3 2 2 3 2 4 4 5 3
Linear Regression Let’s plot these points!! 1 2 3 4 5 6 1 2 3 4 5 x y 1 3 2 2 3 2 4 4 5 3 Mean(xi) = 3
Linear Regression Let’s plot these points!! x y 1 3 2 2 3 2 4 4 5 3 Mean(xi) = 3 Mean(yi) = 2.8 1 2 3 4 5 6 1 2 3 4 5
Linear Regression Now, lets find regression equation to find the best fit line! y = mx + c To find this equation for our data, we need to find our slope (m) and coefficient (c)
Linear Regression y = mx + c ( x- xi ) ( y – yi ) ( x- xi ) 2m = x y x- xi y – yi ( x- xi ) 2 ( x- xi ) ( y – yi ) 1 3 -2 0.2 4 -0.4 2 2 -1 -0.8 1 0.8 3 2 0 -0.8 0 0 4 4 1 1.2 1 1.2 5 3 2 0.2 4 0.4
Linear Regression y = mx + c ( x- xi ) ( y – yi ) ( x- xi ) 2m = x y x- xi y – yi ( x- xi ) 2 ( x- xi ) ( y – yi ) 1 3 -2 0.2 4 -0.4 2 2 -1 -0.8 1 0.8 3 2 0 -0.8 0 0 4 4 1 1.2 1 1.2 5 3 2 0.2 4 0.4 Total = 2Total = 10
y = mx + c ( x- xi ) ( y – yi ) ( x- xi ) 2m = x y x- xi y – yi ( x- xi ) 2 ( x- xi ) ( y – yi ) 1 3 -2 0.2 4 -0.4 2 2 -1 -0.8 1 0.8 3 2 0 -0.8 0 0 4 4 1 1.2 1 1.2 5 3 2 0.2 4 0.4 Total = 2Total = 10 = 2/10 = 0.2 Linear Regression
Linear Regression y = mx + c ( x- xi ) ( y – yi ) ( x- xi ) 2m = = 2/10 = 0.2 y = 0.2 x + c 2.8 = 0.2 * 3 + c 2.8 = 0.6 + c c = 2.8 - 0.6 c = 2.2 So, we can calculate the value of c Mean values = (3, 2.8)
Linear Regression Hence this is our regression line! y = ( 0.2 *x ) + 2.2 1 2 3 4 5 6 1 2 3 4 5
Linear Regression Now, let’s predict the values of y using x = {1,2,3,4,5} and plot the points! y = ( 0.2 *x ) + 2.2 yp = (0.2 * 1) + 2.2 = 2.4 yp = (0.2 * 2) + 2.2 = 2.6 yp = (0.2 * 3) + 2.2 = 2.8 yp = (0.2 * 4) + 2.2 = 3.0 yp = (0.2 * 5) + 2.2 = 3.2 yp = Predicted values of y
Linear Regression Plot the predicted values along with the actual values to see the difference 1 2 3 4 5 6 1 2 3 4 5 - - -- Error Error Error Error x y yp 1 3 2.4 2 2 2.6 3 2 2.8 4 4 3 5 3 3.2 x y
Linear Regression So, our goal is to reduce this error! 1 2 3 4 5 6 1 2 3 4 5 - - -- Error Error Error Error
Linear Regression Minimizing the Distance: There are lots of ways to minimize the distance between the line and the data points like Sum of Squared errors, Sum of Absolute errors, Root Mean Square error etc. We keep moving this line through the data points to make sure the best fit line has the least square distance between the data points and the regression line
Decision Trees Decision Tree is a tree shaped algorithm used to determine a course of action Each branch of the tree represents a possible decision, occurrence or reaction
Decision Trees We have a data which tells us if it is a good day to play golf! Outlook Temp Humidity Windy Play Golf Rainy Hot High FALSE No Rainy Hot High TRUE No Overcast Hot High FALSE Yes Sunny Mild High FALSE Yes Sunny Cool Normal FALSE Yes Sunny Cool Normal TRUE No Overcast Cool Normal TRUE Yes Rainy Mild High FALSE No Rainy Cool Normal FALSE Yes Sunny Mild Normal FALSE Yes Rainy Mild Normal TRUE Yes Overcast Mild High TRUE Yes Overcast Hot Normal FALSE Yes Sunny Mild High TRUE No
Decision Trees Let’s determine if you should play golf when the day is sunny and windy?
Decision Trees Suppose, we draw our tree like this! Humidity Normal High Sunny Outlook Overcast Rainy Play Don’t Play Play Don’t Play
Decision Trees But, is this the right decision tree? For that, we should calculate Entropy and Information Gain! Entropy is the measure of randomness or ‘impurity’ in the dataset Entropy It is the measure of decrease in entropy after the dataset is split Also known as Entropy Reduction Information Gain Entropy should be low! Information Gain should be high!
Decision Trees Let’s look at entropy! Better quality image will be replaced
Decision Trees Let’s look at entropy! = E(5,9) = I(5/14, 9/14) = I(0.36, 0.64) = -(0.36 log2 0.36) – (0.64 log2 0.64) = 0.94 Play Golf Yes No 9 5 Total = 14 Entropy (Play golf) a) Entropy of target class of the dataset (whole entropy):
Decision Trees Let’s look at entropy! Entropy (Play golf, Outlook) = P(sunny) * E (3,2) + P(Overcast) * E(4,0) + P(rainy) * E(2,3) = 5/14 * I(3,2) + 4/14 * I(4,0) + 5/14 * I(2,3) = 0.693 Similarly, we can calculate the entropy of other predictors like Temperature, Humidity, Windy! Play Golf Predictors Yes No Total Outlook Sunny 3 2 5 Overcast 4 0 4 Rainy 2 3 5 14
Decision Trees Now, let’s look at Information Gain! Gain(Outlook) = Entropy(PlayGolf) − Entropy(PlayGolf,Outlook) = 0.940−0.693 =0.247 The information gain of the other three attributes can be calculated in the same way: Gain(Temp) = Entropy(PlayGolf)−Entropy(PlayGolf,Temp) = 0.029 Gain(Humidity) = Entropy(PlayGolf)−Entropy(PlayGolf,Humidity) = 0.152 Gain(Windy) = Entropy(PlayGolf)−Entropy(PlayGolf,Windy) = 0.048
Decision Trees Now, let’s build the decision tree! We choose the attribute with largest information gain as the root node Sunny Outlook Overcast Rainy Windy TrueFalse Don’t Play Play Play Don’t Play Root Node Branch Node Leaf Nodes
Decision Trees So, we wanted to know if it’s a good day to play golf when it’s sunny and windy! Sunny Outlook Overcast Rainy Windy TrueFalse Don’t Play Play Play Don’t Play
Decision Trees So, we wanted to know if it’s a good day to play golf when it’s sunny and windy! Sunny Outlook Overcast Rainy Windy TrueFalse Don’t Play Play Play Don’t Play
Decision Trees Uh-Oh, it’s not a good day to play golf! You can watch a golf game at home! :D
Support Vector Machine Support Vector Machine is a widely used classification algorithm! The idea of Support Vector Machines is simple: The algorithm creates a separation line which divides the classes in the best possible manner For example, dog or cat, disease or no disease
Support Vector Machine Weight Height Suppose, we have labeled sample data, which tells height and weight of males and females
Support Vector Machine How can a machine classify whether a new data point is a male or a female? A new data point Height Weight
Support Vector Machine We draw decision lines, but if we consider decision line 1 then we will classify it as a male Line 1 Height Weight
Support Vector Machine And if we consider decision line 2, then it will be a female! Line 1 Line 2 Height Weight
Support Vector Machine We need to know which line divides the classes correctly, but how? Line 1 Line 2 Height Weight
Support Vector Machine The goal is to choose a hyperplane with the greatest possible margin between the decision line and the nearest point within the training set Height Line 1 Support Vectors Distance Margin: The distance between the hyperplane and the nearest data point from either set Weight
Support Vector Machine When we draw the hyperplanes, we observe that Line 1 has the maximum distance margin so it will classify the new data point correctly Height Line 1 Result: New data point is male! Weight Support Vectors
Support Vector Machine Let’s understand this with the help of an example!
Support Vector Machine Problem Statement: Classifying muffin and cupcake recipes using support vector machines VS
Support Vector Machine Let’s have a look at our dataset: Type Flour Milk Sugar Butter Egg Baking Powder Vanilla Salt Muffin 55 28 3 7 5 2 0 0 Muffin 47 24 12 6 9 1 0 0 Muffin 47 23 18 6 4 1 0 0 Muffin 45 11 17 17 8 1 0 0 Muffin 50 25 12 6 5 2 1 0 Muffin 55 27 3 7 5 2 1 0 Muffin 54 27 7 5 5 2 0 0 Muffin 47 26 10 10 4 1 0 0 Muffin 50 17 17 8 6 1 0 0 Muffin 50 17 17 11 4 1 0 0 Cupcake 39 0 26 19 14 1 1 0 Cupcake 42 21 16 10 8 3 0 0 Cupcake 34 17 20 20 5 2 1 0 Cupcake 39 13 17 19 10 1 1 0 Cupcake 38 15 23 15 8 0 1 0 Cupcake 42 18 25 9 5 1 0 0 Cupcake 36 14 21 14 11 2 1 0 Cupcake 38 15 31 8 6 1 1 0 Cupcake 36 16 24 12 9 1 1 0 Cupcake 34 17 23 11 13 0 1 0
Support Vector Machine Let’s have a look at our dataset: Type Flour Milk Sugar Butter Egg Baking Powder Vanilla Salt Muffin 55 28 3 7 5 2 0 0 Muffin 47 24 12 6 9 1 0 0 Muffin 47 23 18 6 4 1 0 0 Muffin 45 11 17 17 8 1 0 0 Muffin 50 25 12 6 5 2 1 0 Muffin 55 27 3 7 5 2 1 0 Muffin 54 27 7 5 5 2 0 0 Muffin 47 26 10 10 4 1 0 0 Muffin 50 17 17 8 6 1 0 0 Muffin 50 17 17 11 4 1 0 0 Cupcake 39 0 26 19 14 1 1 0 Cupcake 42 21 16 10 8 3 0 0 Cupcake 34 17 20 20 5 2 1 0 Cupcake 39 13 17 19 10 1 1 0 Cupcake 38 15 23 15 8 0 1 0 Cupcake 42 18 25 9 5 1 0 0 Cupcake 36 14 21 14 11 2 1 0 Cupcake 38 15 31 8 6 1 1 0 Cupcake 36 16 24 12 9 1 1 0 Cupcake 34 17 23 11 13 0 1 0 What's the difference between a muffin and a cupcake? Turns out muffins have more flour, while cupcakes have more butter and sugar
Support Vector Machine
Support Vector Machine
Support Vector Machine
Support Vector Machine
Support Vector Machine
Support Vector Machine
Support Vector Machine
Support Vector Machine
Support Vector Machine
Support Vector Machine
Support Vector Machine
Support Vector Machine Hence, we have built a classifier using SVM which is able to classify if a recipe is of a cupcake or a muffin!
Key Takeways What is machine learning? Classification using SVMBuilding a Decision tree Regression-Line of best fitTypes of Machine learning
Machine Learning Tutorial Part - 1 | Machine Learning Tutorial For Beginners Part - 1 | Simplilearn

More Related Content

PPTX
Machine Learning Tutorial | Machine Learning Basics | Machine Learning Algori...
bySimplilearn
 
PPTX
Machine Learning
byGirish Khanzode
 
PPTX
Machine Learning Tutorial Part - 2 | Machine Learning Tutorial For Beginners ...
bySimplilearn
 
PPTX
Machine Learning Algorithms | Machine Learning Tutorial | Data Science Algori...
bySimplilearn
 
PDF
What is Machine Learning | Introduction to Machine Learning | Machine Learnin...
bySimplilearn
 
PPTX
Machine learning
byeonx_32
 
PPTX
What Is Machine Learning? | What Is Machine Learning And How Does It Work? | ...
bySimplilearn
 
PPTX
Supervised and Unsupervised Learning In Machine Learning | Machine Learning T...
bySimplilearn
 
Machine Learning Tutorial | Machine Learning Basics | Machine Learning Algori...
bySimplilearn
 
Machine Learning
byGirish Khanzode
 
Machine Learning Tutorial Part - 2 | Machine Learning Tutorial For Beginners ...
bySimplilearn
 
Machine Learning Algorithms | Machine Learning Tutorial | Data Science Algori...
bySimplilearn
 
What is Machine Learning | Introduction to Machine Learning | Machine Learnin...
bySimplilearn
 
Machine learning
byeonx_32
 
What Is Machine Learning? | What Is Machine Learning And How Does It Work? | ...
bySimplilearn
 
Supervised and Unsupervised Learning In Machine Learning | Machine Learning T...
bySimplilearn
 

What's hot

PPTX
Intro/Overview on Machine Learning Presentation
byAnkit Gupta
 
PDF
Machine learning
byAmit Kumar Rathi
 
PDF
Data preprocessing using Machine Learning
byGopal Sakarkar
 
PDF
Scikit Learn Tutorial | Machine Learning with Python | Python for Data Scienc...
byEdureka!
 
PDF
Machine Learning
byShrey Malik
 
PPTX
Machine learning seminar ppt
byRAHUL DANGWAL
 
PPTX
Machine Learning
byKumar P
 
PPTX
Machine learning
byADARSHMISHRA126
 
PDF
Machine Learning Course | Edureka
byEdureka!
 
PPTX
Presentation on supervised learning
byTonmoy Bhagawati
 
PDF
Feature selection
byDong Guo
 
PDF
Machine Learning Algorithms | Machine Learning Tutorial | Data Science Tutori...
byEdureka!
 
PPTX
Feature selection
bydkpawar
 
PDF
Machine Learning in 10 Minutes | What is Machine Learning? | Edureka
byEdureka!
 
PPTX
supervised learning
byAmar Tripathi
 
PPTX
Introduction to Machine Learning
byRahul Jain
 
PPTX
Machine Can Think
byRahul Jaiman
 
PDF
Classification Based Machine Learning Algorithms
byMd. Main Uddin Rony
 
PPTX
Classification and Regression
byMegha Sharma
 
PPT
Machine Learning
byRahul Kumar
 
Intro/Overview on Machine Learning Presentation
byAnkit Gupta
 
Machine learning
byAmit Kumar Rathi
 
Data preprocessing using Machine Learning
byGopal Sakarkar
 
Scikit Learn Tutorial | Machine Learning with Python | Python for Data Scienc...
byEdureka!
 
Machine Learning
byShrey Malik
 
Machine learning seminar ppt
byRAHUL DANGWAL
 
Machine Learning
byKumar P
 
Machine learning
byADARSHMISHRA126
 
Machine Learning Course | Edureka
byEdureka!
 
Presentation on supervised learning
byTonmoy Bhagawati
 
Feature selection
byDong Guo
 
Machine Learning Algorithms | Machine Learning Tutorial | Data Science Tutori...
byEdureka!
 
Feature selection
bydkpawar
 
Machine Learning in 10 Minutes | What is Machine Learning? | Edureka
byEdureka!
 
supervised learning
byAmar Tripathi
 
Introduction to Machine Learning
byRahul Jain
 
Machine Can Think
byRahul Jaiman
 
Classification Based Machine Learning Algorithms
byMd. Main Uddin Rony
 
Classification and Regression
byMegha Sharma
 
Machine Learning
byRahul Kumar
 

Similar to Machine Learning Tutorial Part - 1 | Machine Learning Tutorial For Beginners Part - 1 | Simplilearn

PDF
Introduction to machine learning
bySanghamitra Deb
 
PPTX
Introduction to machine learning and model building using linear regression
byGirish Gore
 
PDF
Machine learning Introduction
byKuppusamy P
 
PDF
Linear Regression
bySourajitMaity1
 
PPTX
UNIT II SUPERVISED LEARNING - Introduction
byjkowsysara
 
PPTX
Ml ppt at
bypradeep kumar
 
PPTX
Machine learning and linear regression programming
bySoumya Mukherjee
 
PPTX
06-01 Machine Learning and Linear Regression.pptx
bySaharA84
 
DOCX
Essentials of machine learning algorithms
byArunangsu Sahu
 
PDF
Machine Learning.pdf
byUniversity of Sindh
 
PPTX
for minor Introduction_to_Machine_Learning.pptx
byAnonymousvopE9EmDF
 
PDF
مدخل إلى تعلم الآلة
byFares Al-Qunaieer
 
PPTX
Machine learning notes for arts and engg
bygomathis410
 
PDF
Machine Learning deep learning artificial
byAlaaShorbaji1
 
PPTX
Difference between Supervised and Unsupervised Machine Learning.pptx
byImranAhmed929269
 
PPTX
Accuracy & Performance in Machine Learning (1).pptx
byshahashtar72
 
PDF
3ml.pdf
byMianAdnan27
 
PPTX
Lecture 8 about data mining and how to use it.pptx
byHedraAtif
 
PPTX
MACHINE LEARNING.pptx
bySOURAVGHOSH623569
 
PPTX
Linear Regression for Data Mining Application
bySudiptaDas684406
 
Introduction to machine learning
bySanghamitra Deb
 
Introduction to machine learning and model building using linear regression
byGirish Gore
 
Machine learning Introduction
byKuppusamy P
 
Linear Regression
bySourajitMaity1
 
UNIT II SUPERVISED LEARNING - Introduction
byjkowsysara
 
Ml ppt at
bypradeep kumar
 
Machine learning and linear regression programming
bySoumya Mukherjee
 
06-01 Machine Learning and Linear Regression.pptx
bySaharA84
 
Essentials of machine learning algorithms
byArunangsu Sahu
 
Machine Learning.pdf
byUniversity of Sindh
 
for minor Introduction_to_Machine_Learning.pptx
byAnonymousvopE9EmDF
 
مدخل إلى تعلم الآلة
byFares Al-Qunaieer
 
Machine learning notes for arts and engg
bygomathis410
 
Machine Learning deep learning artificial
byAlaaShorbaji1
 
Difference between Supervised and Unsupervised Machine Learning.pptx
byImranAhmed929269
 
Accuracy & Performance in Machine Learning (1).pptx
byshahashtar72
 
3ml.pdf
byMianAdnan27
 
Lecture 8 about data mining and how to use it.pptx
byHedraAtif
 
MACHINE LEARNING.pptx
bySOURAVGHOSH623569
 
Linear Regression for Data Mining Application
bySudiptaDas684406
 

More from Simplilearn

PPTX
Top 50 Scrum Master Interview Questions | Scrum Master Interview Questions & ...
bySimplilearn
 
PPTX
Bagging Vs Boosting In Machine Learning | Ensemble Learning In Machine Learni...
bySimplilearn
 
PPTX
Future Of Social Media | Social Media Trends and Strategies 2025 | Instagram ...
bySimplilearn
 
PPTX
SQL Query Optimization | SQL Query Optimization Techniques | SQL Basics | SQL...
bySimplilearn
 
PPTX
SQL INterview Questions .pTop 45 SQL Interview Questions And Answers In 2025 ...
bySimplilearn
 
PPTX
How To Start Influencer Marketing Business | Influencer Marketing For Beginne...
bySimplilearn
 
PPTX
Cyber Security Roadmap 2025 | How To Become Cyber Security Engineer In 2025 |...
bySimplilearn
 
PPTX
How To Become An AI And ML Engineer In 2025 | AI Engineer Roadmap | AI ML Car...
bySimplilearn
 
PPTX
What Is GitHub Copilot? | How To Use GitHub Copilot? | How does GitHub Copilo...
bySimplilearn
 
PPTX
Top 10 Data Analyst Certification For 2025 | Best Data Analyst Certification ...
bySimplilearn
 
PPTX
Complete Data Science Roadmap For 2025 | Data Scientist Roadmap For Beginners...
bySimplilearn
 
PPTX
Top 7 High Paying AI Certifications Courses For 2025 | Best AI Certifications...
bySimplilearn
 
PPTX
Data Cleaning In Data Mining | Step by Step Data Cleaning Process | Data Clea...
bySimplilearn
 
PPTX
Top 10 Data Analyst Projects For 2025 | Data Analyst Projects | Data Analysis...
bySimplilearn
 
PPTX
AI Engineer Roadmap 2025 | AI Engineer Roadmap For Beginners | AI Engineer Ca...
bySimplilearn
 
PPTX
Machine Learning Roadmap 2025 | Machine Learning Engineer Roadmap For Beginne...
bySimplilearn
 
PPTX
Kotter's 8-Step Change Model Explained | Kotter's Change Management Model | S...
bySimplilearn
 
PPTX
Gen AI Engineer Roadmap For 2025 | How To Become Gen AI Engineer In 2025 | Si...
bySimplilearn
 
PPTX
Top 10 Data Analyst Certification For 2025 | Best Data Analyst Certification ...
bySimplilearn
 
PPTX
Complete Data Science Roadmap For 2025 | Data Scientist Roadmap For Beginners...
bySimplilearn
 
Top 50 Scrum Master Interview Questions | Scrum Master Interview Questions & ...
bySimplilearn
 
Bagging Vs Boosting In Machine Learning | Ensemble Learning In Machine Learni...
bySimplilearn
 
Future Of Social Media | Social Media Trends and Strategies 2025 | Instagram ...
bySimplilearn
 
SQL Query Optimization | SQL Query Optimization Techniques | SQL Basics | SQL...
bySimplilearn
 
SQL INterview Questions .pTop 45 SQL Interview Questions And Answers In 2025 ...
bySimplilearn
 
How To Start Influencer Marketing Business | Influencer Marketing For Beginne...
bySimplilearn
 
Cyber Security Roadmap 2025 | How To Become Cyber Security Engineer In 2025 |...
bySimplilearn
 
How To Become An AI And ML Engineer In 2025 | AI Engineer Roadmap | AI ML Car...
bySimplilearn
 
What Is GitHub Copilot? | How To Use GitHub Copilot? | How does GitHub Copilo...
bySimplilearn
 
Top 10 Data Analyst Certification For 2025 | Best Data Analyst Certification ...
bySimplilearn
 
Complete Data Science Roadmap For 2025 | Data Scientist Roadmap For Beginners...
bySimplilearn
 
Top 7 High Paying AI Certifications Courses For 2025 | Best AI Certifications...
bySimplilearn
 
Data Cleaning In Data Mining | Step by Step Data Cleaning Process | Data Clea...
bySimplilearn
 
Top 10 Data Analyst Projects For 2025 | Data Analyst Projects | Data Analysis...
bySimplilearn
 
AI Engineer Roadmap 2025 | AI Engineer Roadmap For Beginners | AI Engineer Ca...
bySimplilearn
 
Machine Learning Roadmap 2025 | Machine Learning Engineer Roadmap For Beginne...
bySimplilearn
 
Kotter's 8-Step Change Model Explained | Kotter's Change Management Model | S...
bySimplilearn
 
Gen AI Engineer Roadmap For 2025 | How To Become Gen AI Engineer In 2025 | Si...
bySimplilearn
 
Top 10 Data Analyst Certification For 2025 | Best Data Analyst Certification ...
bySimplilearn
 
Complete Data Science Roadmap For 2025 | Data Scientist Roadmap For Beginners...
bySimplilearn
 

Recently uploaded

PDF
Darwinism: Theory of Natural Selection and Origin of Species
byIPGDCWA,NAMPALLY
 
PDF
West Hatch High School - GCSE French Specification
byWestHatch
 
PDF
TỔNG HỢP 156 ĐỀ CHÍNH THỨC KỲ THI CHỌN HỌC SINH GIỎI TIẾNG ANH LỚP 12 CÁC TỈN...
byNguyen Thanh Tu Collection
 
PPTX
Toba Tek Singh - Visualising Partition through Manto's Lens
bymiraljoshi48
 
PPTX
How to Create & Automate Asset Model in Odoo 18 Accounting
byCeline George
 
PDF
APPSC APPSC Forest Draughtsman GS Question paper.pdf
byssuser9d8e4e
 
PPTX
literary theory and criticism by Vivek p
byvivekrathodborda
 
PPTX
" Jaya : Silence as Resistance " - That long silence
bydharabhandari35
 
PDF
Q4_LE_English 5_Lesson 1_Week 1.pdf learning instruction
byMichelleCajefe2
 
PPTX
Mohan - "A man of silence and authority"
bynidhibachauhan46
 
PPTX
"Aristotle : Father Of Western Philosophy"
bymitalbarathod28
 
PPTX
'Colonial Mentality and Social Identity in Karma by Khushwant Singh'
byKrishnarajsinh Parmar
 
PPTX
Appreciations - Jan 26 01.pptxkkkmmkmkmkmkm
bypreetheshparmar
 
PPTX
Master of Punjabi Short Story "kartar singh duggal
bybhautikbharwad4
 
PPTX
West Hatch High School - GCSE Media Studies
byWestHatch
 
PPTX
How Physician Assistants in the USA Earn CME Credits Online.pptx
byCME4Life
 
PDF
Sharad Bisen_Irrigation Systems and Methods in Horticultural Crops.pdf
bybisensharad
 
PPTX
West Hatch High School -- GCSE Geography
byWestHatch
 
PPTX
West Hatch High School: Year 9 Art Course
byWestHatch
 
PDF
Schrodinger's Capital Finals (SciBiz Quiz).pdf
byConquiztadors- the Quiz Society of Sri Venkateswara College
 
Darwinism: Theory of Natural Selection and Origin of Species
byIPGDCWA,NAMPALLY
 
West Hatch High School - GCSE French Specification
byWestHatch
 
TỔNG HỢP 156 ĐỀ CHÍNH THỨC KỲ THI CHỌN HỌC SINH GIỎI TIẾNG ANH LỚP 12 CÁC TỈN...
byNguyen Thanh Tu Collection
 
Toba Tek Singh - Visualising Partition through Manto's Lens
bymiraljoshi48
 
How to Create & Automate Asset Model in Odoo 18 Accounting
byCeline George
 
APPSC APPSC Forest Draughtsman GS Question paper.pdf
byssuser9d8e4e
 
literary theory and criticism by Vivek p
byvivekrathodborda
 
" Jaya : Silence as Resistance " - That long silence
bydharabhandari35
 
Q4_LE_English 5_Lesson 1_Week 1.pdf learning instruction
byMichelleCajefe2
 
Mohan - "A man of silence and authority"
bynidhibachauhan46
 
"Aristotle : Father Of Western Philosophy"
bymitalbarathod28
 
'Colonial Mentality and Social Identity in Karma by Khushwant Singh'
byKrishnarajsinh Parmar
 
Appreciations - Jan 26 01.pptxkkkmmkmkmkmkm
bypreetheshparmar
 
Master of Punjabi Short Story "kartar singh duggal
bybhautikbharwad4
 
West Hatch High School - GCSE Media Studies
byWestHatch
 
How Physician Assistants in the USA Earn CME Credits Online.pptx
byCME4Life
 
Sharad Bisen_Irrigation Systems and Methods in Horticultural Crops.pdf
bybisensharad
 
West Hatch High School -- GCSE Geography
byWestHatch
 
West Hatch High School: Year 9 Art Course
byWestHatch
 
Schrodinger's Capital Finals (SciBiz Quiz).pdf
byConquiztadors- the Quiz Society of Sri Venkateswara College
 

Machine Learning Tutorial Part - 1 | Machine Learning Tutorial For Beginners Part - 1 | Simplilearn

  • 1.
  • 2.
    What’s in itfor you? Why Machine Learning? What is Machine Learning? Types Of Machine Learning Machine Learning Algorithms Linear Regression Decision Trees Support Vector Machine Use Case: Classify whether a recipe is of a cupcake or a muffin using SVM
  • 3.
    Why Machine Learning? BecauseMachine can drive your car for you!! Because Machine can unlock your phone with your face!! Because Machine can now detect 50 eye diseases
  • 4.
  • 5.
    Why Machine Learning? Nobodylikes spam posts on Facebook that annoy them into interacting with likes, shares, comments, and other actions
  • 6.
    Why Machine Learning? Thistactic, known as “Engagement Bait,” takes advantage of Facebook’s Newsfeed algorithm by boosting engagement in order to get greater reach
  • 7.
    To eliminate engagementbait, the company reviewed and categorized hundreds of thousands of posts to train a machine learning model that detects different types of engagement bait Facebook scroll GIF will be replaced New Post Scans the keywords and phrases like “This” and checks the click through rate This is a tag bait! Block this post Data fed to the machine
  • 8.
    Google’s DeepMind project“AlphaGO”, a  computer program that plays the board game ‘GO’ has defeated the world’s number one Go player Ke Jie
  • 9.
    What is MachineLearning? Machine learning is the science of making computers learn and act like humans by feeding data and information without being explicitly programmed! Ordinary System With Artificial Intelligence Machine Learning Learns Predicts Improves
  • 10.
    Define Objective Collect Data PrepareData Select Algorithm Deploy Predict Test Model Train Model 01 02 03 04 05 06 07 08 What is Machine Learning?
  • 11.
    For instance, whetherthe stock price will increase or decrease Do you want to predict a category? That’s classification!
  • 12.
    For instance, predictingthe age of a person based on the height, weight, health and other factors Do you want to predict a quantity? That’s regression!
  • 13.
    For instance, youwant to detect money withdrawal anomalies Do you want to detect an anomaly? That’s anomaly detection!
  • 14.
    For instance: Findinggroups of customers with similar behavior given a large database of customer data containing their demographics and past buying records Do you want to discover structure in unexplored data? That’s clustering
  • 16.
    What do youunderstand from Measures and Dimensions? Each field from the data source is automatically assigned a datatype (such as string, integer) and a role (dimension or measure) Aggregation applied on measures is ‘Sum’ by default but you can always change the default aggregation in the settings Can you tell what’s happening in the following cases? A. Grouping documents into different categories based on the topic and content of each document
  • 17.
    What do youunderstand from Measures and Dimensions? Each field from the data source is automatically assigned a datatype (such as string, integer) and a role (dimension or measure) Aggregation applied on measures is ‘Sum’ by default but you can always change the default aggregation in the settings Can you tell what’s happening in the following cases? A. Grouping documents into different categories based on the topic and content of each document B. Identifying hand-written digits in images correctly
  • 18.
    What do youunderstand from Measures and Dimensions? Each field from the data source is automatically assigned a datatype (such as string, integer) and a role (dimension or measure) Aggregation applied on measures is ‘Sum’ by default but you can always change the default aggregation in the settings Can you tell what’s happening in the following cases? A. Grouping documents into different categories based on the topic and content of each document B. Identifying hand-written digits in images correctly C. Behavior of a website indicating that the site is not working as designed
  • 19.
    What do youunderstand from Measures and Dimensions? Each field from the data source is automatically assigned a datatype (such as string, integer) and a role (dimension or measure) Aggregation applied on measures is ‘Sum’ by default but you can always change the default aggregation in the settings Can you tell what’s happening in the following cases? A. Grouping documents into different categories based on the topic and content of each document B. Identifying hand-written digits in images correctly C. Behavior of a website indicating that the site is not working as designed D. Predicting salary of an individual based his/her years of experience
  • 20.
    Types of MachineLearning Supervised
  • 21.
    Types of MachineLearning Supervised Un-Supervised
  • 22.
    Types of MachineLearning Supervised Reinforcement Un-Supervised
  • 23.
    Supervised Learning Labeled Data ModelTraining New Data Square Circle Prediction Supervised learning is a method used to enable machines to classify/ predict objects, problems or situations based on labeled data fed to the machine Circle Square Triangle Labels
  • 24.
    Unsupervised Learning Unlabled DataOutput In Unsupervised learning, Machine Learning model finds the hidden pattern in an unlabeled data Model Training
  • 25.
    Reinforcement Learning Reinforcement learningis an important type of Machine Learning where an agent learns how to behave in an environment by performing actions and seeing the results ACTION NEW STATE Agent Environment
  • 26.
    Supervised VS Unsupervised Nofeedback Find hidden structure in data Supervised vs Unsupervised Labeled Data Direct feedback Predict output Non-labeled data
  • 27.
    Support Vector Machine LinearRegression Decision Trees Machine Learning Algorithms There are many interesting Machine Learning algorithms, let’s have a look at a few of them
  • 28.
    Linear Regression y =mx + c Linear regression is a linear model, e.g. a model that assumes a linear relationship between the input variables (x) and a single output variable (y) Linear regression is perhaps one of the most well known and well understood algorithms in statistics and machine learning!
  • 29.
    Linear Regression Imagine, weare predicting distance travelled (y) from speed (x). Our linear regression model representation for this problem would be: y = m * x + c Or distance = m * speed + c c = coefficient m = y-intercept
  • 30.
    Speed = 10m/s Distance= 36 km Time is constant
  • 31.
    Speed = 10m/s Distance= 36 km Speed = 20m/s Distance = 52 km Time is constant
  • 32.
    Speed = 10m/s Distance= 36 km Speed = 20m/s Distance = 52 km Speed = 30m/s Distance = ? Time is constant
  • 33.
    Linear Regression Speed Distance y =mx + c Distance travelled in fixed interval of time c = y-intercept of line m = +ve slope of the line As the speed increases, distance also increases, hence the variables have a positive relationship Speed of the person
  • 34.
    Distance is constant Speed= 10m/s Time = 100 s
  • 35.
    Speed = 10m/s Time= 100 s Speed = 20m/s Time = 50 s Distance is constant
  • 36.
    Speed = 10m/s Time= 100 s Speed = 20m/s Time = 50 s Speed = 30m/s Time = ? Distance is constant
  • 37.
    Linear Regression Speed Time y =mx + c Time taken to travel a fixed distance m = -ve slope of the line As the speed increases, time decreases, hence the variables have a negative relationship If distance is assumed to be constant, let’s see the relationship between speed and time Speed of the person
  • 38.
    Linear Regression Let’s seethe mathematical implementation of Linear Regression! Suppose we have a dataset that looks like: x y 1 3 2 2 3 2 4 4 5 3
  • 39.
    Linear Regression Let’s plotthese points!! 1 2 3 4 5 6 1 2 3 4 5 x y 1 3 2 2 3 2 4 4 5 3 Mean(xi) = 3
  • 40.
    Linear Regression Let’s plotthese points!! x y 1 3 2 2 3 2 4 4 5 3 Mean(xi) = 3 Mean(yi) = 2.8 1 2 3 4 5 6 1 2 3 4 5
  • 41.
    Linear Regression Now, letsfind regression equation to find the best fit line! y = mx + c To find this equation for our data, we need to find our slope (m) and coefficient (c)
  • 42.
    Linear Regression y =mx + c ( x- xi ) ( y – yi ) ( x- xi ) 2m = x y x- xi y – yi ( x- xi ) 2 ( x- xi ) ( y – yi ) 1 3 -2 0.2 4 -0.4 2 2 -1 -0.8 1 0.8 3 2 0 -0.8 0 0 4 4 1 1.2 1 1.2 5 3 2 0.2 4 0.4
  • 43.
    Linear Regression y =mx + c ( x- xi ) ( y – yi ) ( x- xi ) 2m = x y x- xi y – yi ( x- xi ) 2 ( x- xi ) ( y – yi ) 1 3 -2 0.2 4 -0.4 2 2 -1 -0.8 1 0.8 3 2 0 -0.8 0 0 4 4 1 1.2 1 1.2 5 3 2 0.2 4 0.4 Total = 2Total = 10
  • 44.
    y = mx+ c ( x- xi ) ( y – yi ) ( x- xi ) 2m = x y x- xi y – yi ( x- xi ) 2 ( x- xi ) ( y – yi ) 1 3 -2 0.2 4 -0.4 2 2 -1 -0.8 1 0.8 3 2 0 -0.8 0 0 4 4 1 1.2 1 1.2 5 3 2 0.2 4 0.4 Total = 2Total = 10 = 2/10 = 0.2 Linear Regression
  • 45.
    Linear Regression y =mx + c ( x- xi ) ( y – yi ) ( x- xi ) 2m = = 2/10 = 0.2 y = 0.2 x + c 2.8 = 0.2 * 3 + c 2.8 = 0.6 + c c = 2.8 - 0.6 c = 2.2 So, we can calculate the value of c Mean values = (3, 2.8)
  • 46.
    Linear Regression Hence thisis our regression line! y = ( 0.2 *x ) + 2.2 1 2 3 4 5 6 1 2 3 4 5
  • 47.
    Linear Regression Now, let’spredict the values of y using x = {1,2,3,4,5} and plot the points! y = ( 0.2 *x ) + 2.2 yp = (0.2 * 1) + 2.2 = 2.4 yp = (0.2 * 2) + 2.2 = 2.6 yp = (0.2 * 3) + 2.2 = 2.8 yp = (0.2 * 4) + 2.2 = 3.0 yp = (0.2 * 5) + 2.2 = 3.2 yp = Predicted values of y
  • 48.
    Linear Regression Plot thepredicted values along with the actual values to see the difference 1 2 3 4 5 6 1 2 3 4 5 - - -- Error Error Error Error x y yp 1 3 2.4 2 2 2.6 3 2 2.8 4 4 3 5 3 3.2 x y
  • 49.
    Linear Regression So, ourgoal is to reduce this error! 1 2 3 4 5 6 1 2 3 4 5 - - -- Error Error Error Error
  • 50.
    Linear Regression Minimizing theDistance: There are lots of ways to minimize the distance between the line and the data points like Sum of Squared errors, Sum of Absolute errors, Root Mean Square error etc. We keep moving this line through the data points to make sure the best fit line has the least square distance between the data points and the regression line
  • 51.
    Decision Trees Decision Treeis a tree shaped algorithm used to determine a course of action Each branch of the tree represents a possible decision, occurrence or reaction
  • 52.
    Decision Trees We havea data which tells us if it is a good day to play golf! Outlook Temp Humidity Windy Play Golf Rainy Hot High FALSE No Rainy Hot High TRUE No Overcast Hot High FALSE Yes Sunny Mild High FALSE Yes Sunny Cool Normal FALSE Yes Sunny Cool Normal TRUE No Overcast Cool Normal TRUE Yes Rainy Mild High FALSE No Rainy Cool Normal FALSE Yes Sunny Mild Normal FALSE Yes Rainy Mild Normal TRUE Yes Overcast Mild High TRUE Yes Overcast Hot Normal FALSE Yes Sunny Mild High TRUE No
  • 53.
    Decision Trees Let’s determineif you should play golf when the day is sunny and windy?
  • 54.
    Decision Trees Suppose, wedraw our tree like this! Humidity Normal High Sunny Outlook Overcast Rainy Play Don’t Play Play Don’t Play
  • 55.
    Decision Trees But, isthis the right decision tree? For that, we should calculate Entropy and Information Gain! Entropy is the measure of randomness or ‘impurity’ in the dataset Entropy It is the measure of decrease in entropy after the dataset is split Also known as Entropy Reduction Information Gain Entropy should be low! Information Gain should be high!
  • 56.
    Decision Trees Let’s lookat entropy! Better quality image will be replaced
  • 57.
    Decision Trees Let’s lookat entropy! = E(5,9) = I(5/14, 9/14) = I(0.36, 0.64) = -(0.36 log2 0.36) – (0.64 log2 0.64) = 0.94 Play Golf Yes No 9 5 Total = 14 Entropy (Play golf) a) Entropy of target class of the dataset (whole entropy):
  • 58.
    Decision Trees Let’s lookat entropy! Entropy (Play golf, Outlook) = P(sunny) * E (3,2) + P(Overcast) * E(4,0) + P(rainy) * E(2,3) = 5/14 * I(3,2) + 4/14 * I(4,0) + 5/14 * I(2,3) = 0.693 Similarly, we can calculate the entropy of other predictors like Temperature, Humidity, Windy! Play Golf Predictors Yes No Total Outlook Sunny 3 2 5 Overcast 4 0 4 Rainy 2 3 5 14
  • 59.
    Decision Trees Now, let’slook at Information Gain! Gain(Outlook) = Entropy(PlayGolf) − Entropy(PlayGolf,Outlook) = 0.940−0.693 =0.247 The information gain of the other three attributes can be calculated in the same way: Gain(Temp) = Entropy(PlayGolf)−Entropy(PlayGolf,Temp) = 0.029 Gain(Humidity) = Entropy(PlayGolf)−Entropy(PlayGolf,Humidity) = 0.152 Gain(Windy) = Entropy(PlayGolf)−Entropy(PlayGolf,Windy) = 0.048
  • 60.
    Decision Trees Now, let’sbuild the decision tree! We choose the attribute with largest information gain as the root node Sunny Outlook Overcast Rainy Windy TrueFalse Don’t Play Play Play Don’t Play Root Node Branch Node Leaf Nodes
  • 61.
    Decision Trees So, wewanted to know if it’s a good day to play golf when it’s sunny and windy! Sunny Outlook Overcast Rainy Windy TrueFalse Don’t Play Play Play Don’t Play
  • 62.
    Decision Trees So, wewanted to know if it’s a good day to play golf when it’s sunny and windy! Sunny Outlook Overcast Rainy Windy TrueFalse Don’t Play Play Play Don’t Play
  • 63.
    Decision Trees Uh-Oh, it’snot a good day to play golf! You can watch a golf game at home! :D
  • 64.
    Support Vector Machine SupportVector Machine is a widely used classification algorithm! The idea of Support Vector Machines is simple: The algorithm creates a separation line which divides the classes in the best possible manner For example, dog or cat, disease or no disease
  • 65.
    Support Vector Machine Weight Height Suppose,we have labeled sample data, which tells height and weight of males and females
  • 66.
    Support Vector Machine Howcan a machine classify whether a new data point is a male or a female? A new data point Height Weight
  • 67.
    Support Vector Machine Wedraw decision lines, but if we consider decision line 1 then we will classify it as a male Line 1 Height Weight
  • 68.
    Support Vector Machine Andif we consider decision line 2, then it will be a female! Line 1 Line 2 Height Weight
  • 69.
    Support Vector Machine Weneed to know which line divides the classes correctly, but how? Line 1 Line 2 Height Weight
  • 70.
    Support Vector Machine Thegoal is to choose a hyperplane with the greatest possible margin between the decision line and the nearest point within the training set Height Line 1 Support Vectors Distance Margin: The distance between the hyperplane and the nearest data point from either set Weight
  • 71.
    Support Vector Machine Whenwe draw the hyperplanes, we observe that Line 1 has the maximum distance margin so it will classify the new data point correctly Height Line 1 Result: New data point is male! Weight Support Vectors
  • 72.
    Support Vector Machine Let’sunderstand this with the help of an example!
  • 73.
    Support Vector Machine ProblemStatement: Classifying muffin and cupcake recipes using support vector machines VS
  • 74.
    Support Vector Machine Let’shave a look at our dataset: Type Flour Milk Sugar Butter Egg Baking Powder Vanilla Salt Muffin 55 28 3 7 5 2 0 0 Muffin 47 24 12 6 9 1 0 0 Muffin 47 23 18 6 4 1 0 0 Muffin 45 11 17 17 8 1 0 0 Muffin 50 25 12 6 5 2 1 0 Muffin 55 27 3 7 5 2 1 0 Muffin 54 27 7 5 5 2 0 0 Muffin 47 26 10 10 4 1 0 0 Muffin 50 17 17 8 6 1 0 0 Muffin 50 17 17 11 4 1 0 0 Cupcake 39 0 26 19 14 1 1 0 Cupcake 42 21 16 10 8 3 0 0 Cupcake 34 17 20 20 5 2 1 0 Cupcake 39 13 17 19 10 1 1 0 Cupcake 38 15 23 15 8 0 1 0 Cupcake 42 18 25 9 5 1 0 0 Cupcake 36 14 21 14 11 2 1 0 Cupcake 38 15 31 8 6 1 1 0 Cupcake 36 16 24 12 9 1 1 0 Cupcake 34 17 23 11 13 0 1 0
  • 75.
    Support Vector Machine Let’shave a look at our dataset: Type Flour Milk Sugar Butter Egg Baking Powder Vanilla Salt Muffin 55 28 3 7 5 2 0 0 Muffin 47 24 12 6 9 1 0 0 Muffin 47 23 18 6 4 1 0 0 Muffin 45 11 17 17 8 1 0 0 Muffin 50 25 12 6 5 2 1 0 Muffin 55 27 3 7 5 2 1 0 Muffin 54 27 7 5 5 2 0 0 Muffin 47 26 10 10 4 1 0 0 Muffin 50 17 17 8 6 1 0 0 Muffin 50 17 17 11 4 1 0 0 Cupcake 39 0 26 19 14 1 1 0 Cupcake 42 21 16 10 8 3 0 0 Cupcake 34 17 20 20 5 2 1 0 Cupcake 39 13 17 19 10 1 1 0 Cupcake 38 15 23 15 8 0 1 0 Cupcake 42 18 25 9 5 1 0 0 Cupcake 36 14 21 14 11 2 1 0 Cupcake 38 15 31 8 6 1 1 0 Cupcake 36 16 24 12 9 1 1 0 Cupcake 34 17 23 11 13 0 1 0 What's the difference between a muffin and a cupcake? Turns out muffins have more flour, while cupcakes have more butter and sugar
  • 76.
  • 77.
  • 78.
  • 79.
  • 80.
  • 81.
  • 82.
  • 83.
  • 84.
  • 85.
  • 86.
  • 87.
    Support Vector Machine Hence,we have built a classifier using SVM which is able to classify if a recipe is of a cupcake or a muffin!
  • 88.
    Key Takeways What ismachine learning? Classification using SVMBuilding a Decision tree Regression-Line of best fitTypes of Machine learning

Editor's Notes

  • #3 Style - 01
  • #4 We can talk about how AI enabled machines are able to detect major diseases these days etc
  • #5 Remove title case
  • #6 Remove title case
  • #7 Remove title case
  • #8 Remove title case
  • #9 Hence, Machine learning is being used to reduce the spread of content that is spammy, sensational, or misleading in order to promote more meaningful and authentic conversations on Facebook
  • #10 Remove title case
  • #11 Remove title case
  • #12 Remove title case
  • #13 Remove title case
  • #14 Remove title case
  • #15 Remove title case
  • #16 Remove title case
  • #17 Style - 01
  • #18 Style - 01
  • #19 Style - 01
  • #20 Style - 01
  • #21 Remove title case
  • #22 Remove title case
  • #23 Remove title case
  • #24 Remove title case
  • #25 Remove title case
  • #26 Remove title case
  • #27 Remove title case
  • #29 Remove title case
  • #30 Remove title case
  • #34 Remove title case
  • #38 Remove title case
  • #39 Remove title case
  • #40 Remove title case
  • #41 Remove title case
  • #42 Remove title case
  • #43 Remove title case
  • #44 Remove title case
  • #45 Remove title case
  • #46 Remove title case
  • #47 Remove title case
  • #48 Remove title case
  • #49 Remove title case
  • #50 Remove title case
  • #51 Remove title case
  • #52 Remove title case
  • #53 Remove title case
  • #54 Remove title case
  • #55 Remove title case
  • #56 Remove title case
  • #57 Remove title case
  • #58 Remove title case
  • #59 Remove title case
  • #60 Remove title case
  • #61 Remove title case
  • #62 Remove title case
  • #63 Remove title case
  • #64 Remove title case
  • #65 Remove title case
  • #66 Remove title case
  • #67 Remove title case
  • #68 Remove title case
  • #69 Remove title case
  • #70  a hyperplane as a line that linearly separates and classifies a set of data
  • #71  a hyperplane as a line that linearly separates and classifies a set of data
  • #72  a hyperplane as a line that linearly separates and classifies a set of data
  • #73 Remove title case
  • #74 Remove title case
  • #75 Remove title case
  • #76 Remove title case
  • #77 Remove title case
  • #78 Remove title case
  • #79 Remove title case
  • #80 Remove title case
  • #81 Remove title case
  • #82 Remove title case
  • #83 Remove title case
  • #84 Remove title case
  • #85 Remove title case
  • #86 Remove title case
  • #87 Remove title case
  • #88 Remove title case