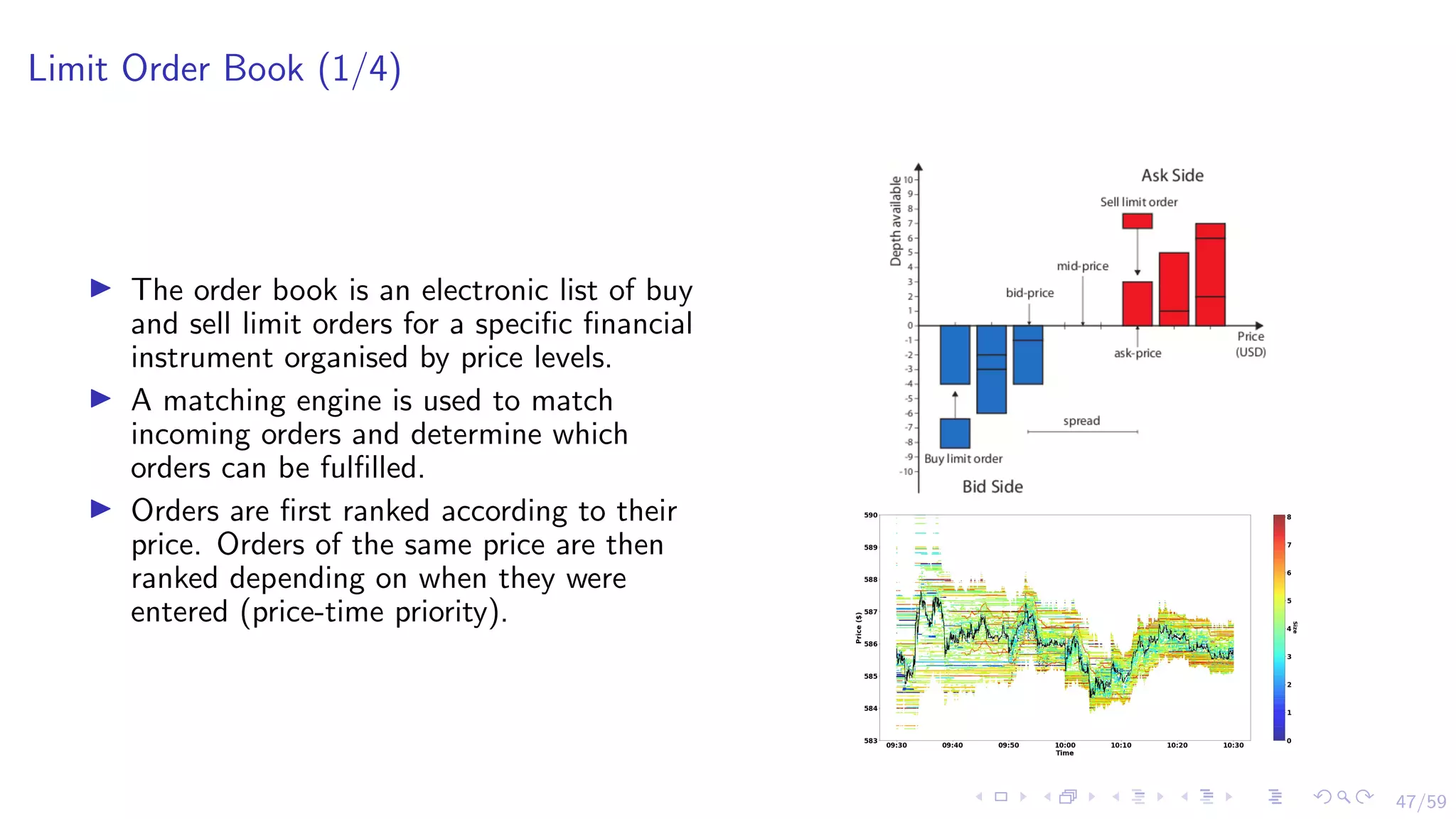
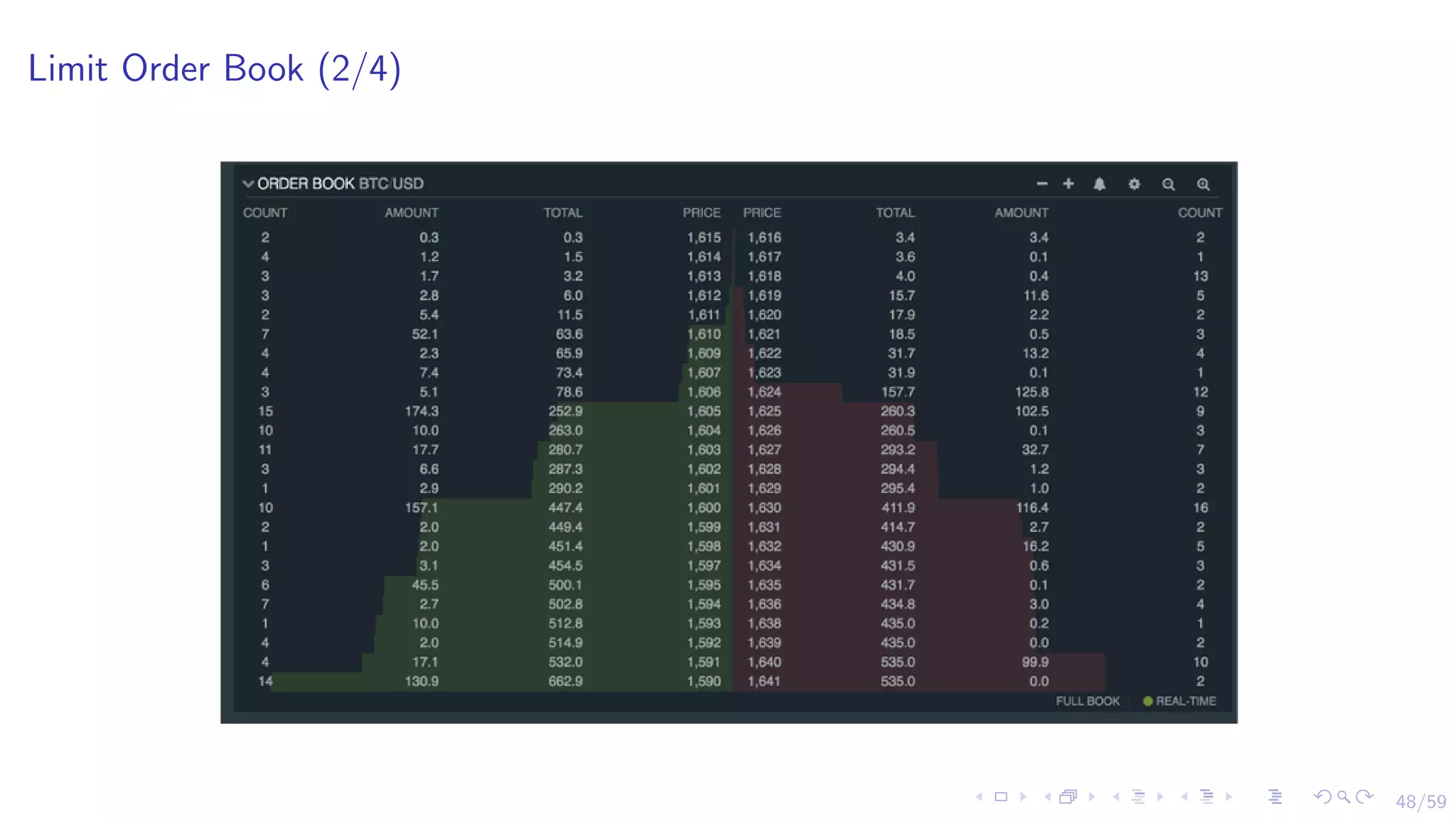
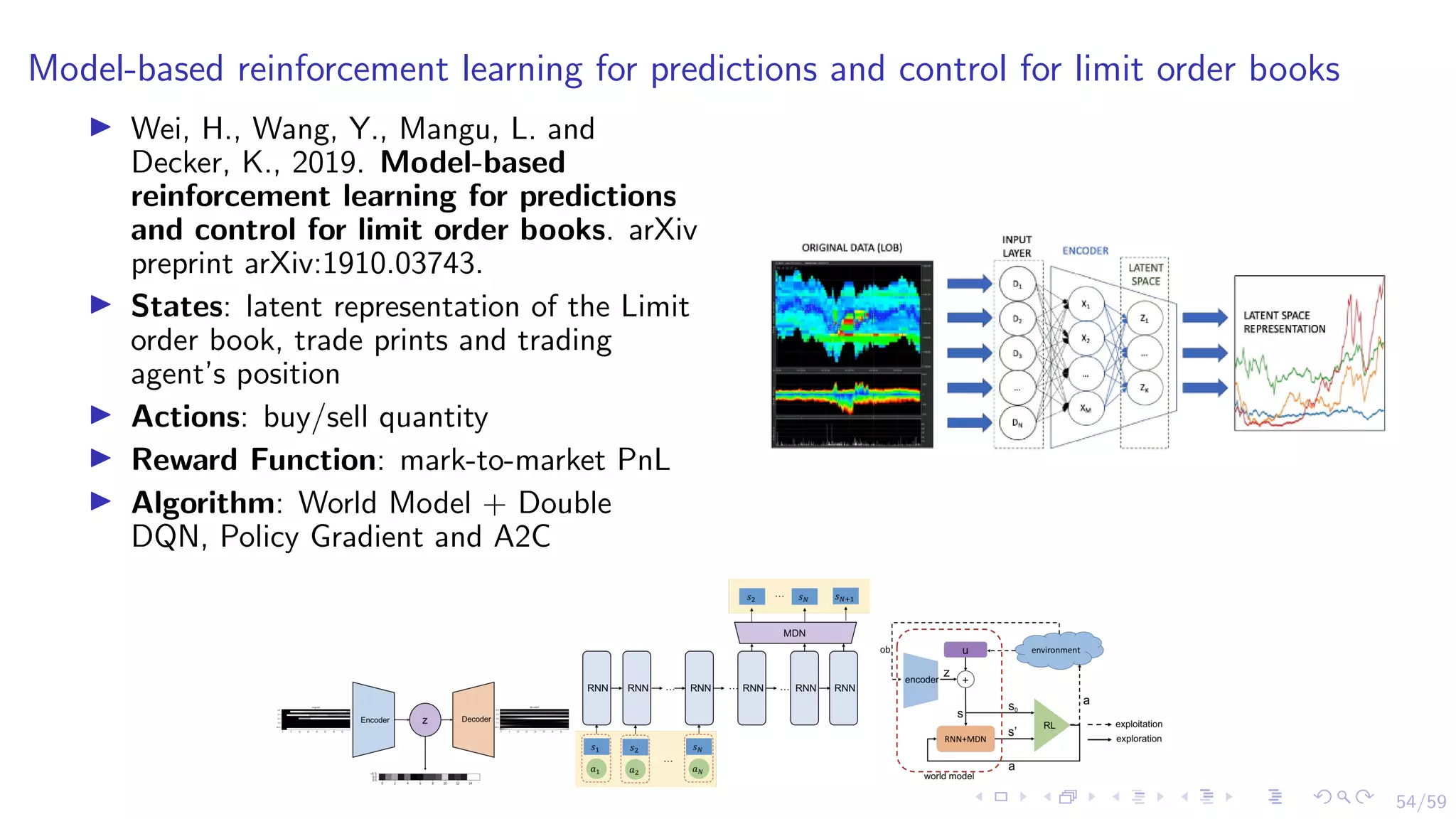
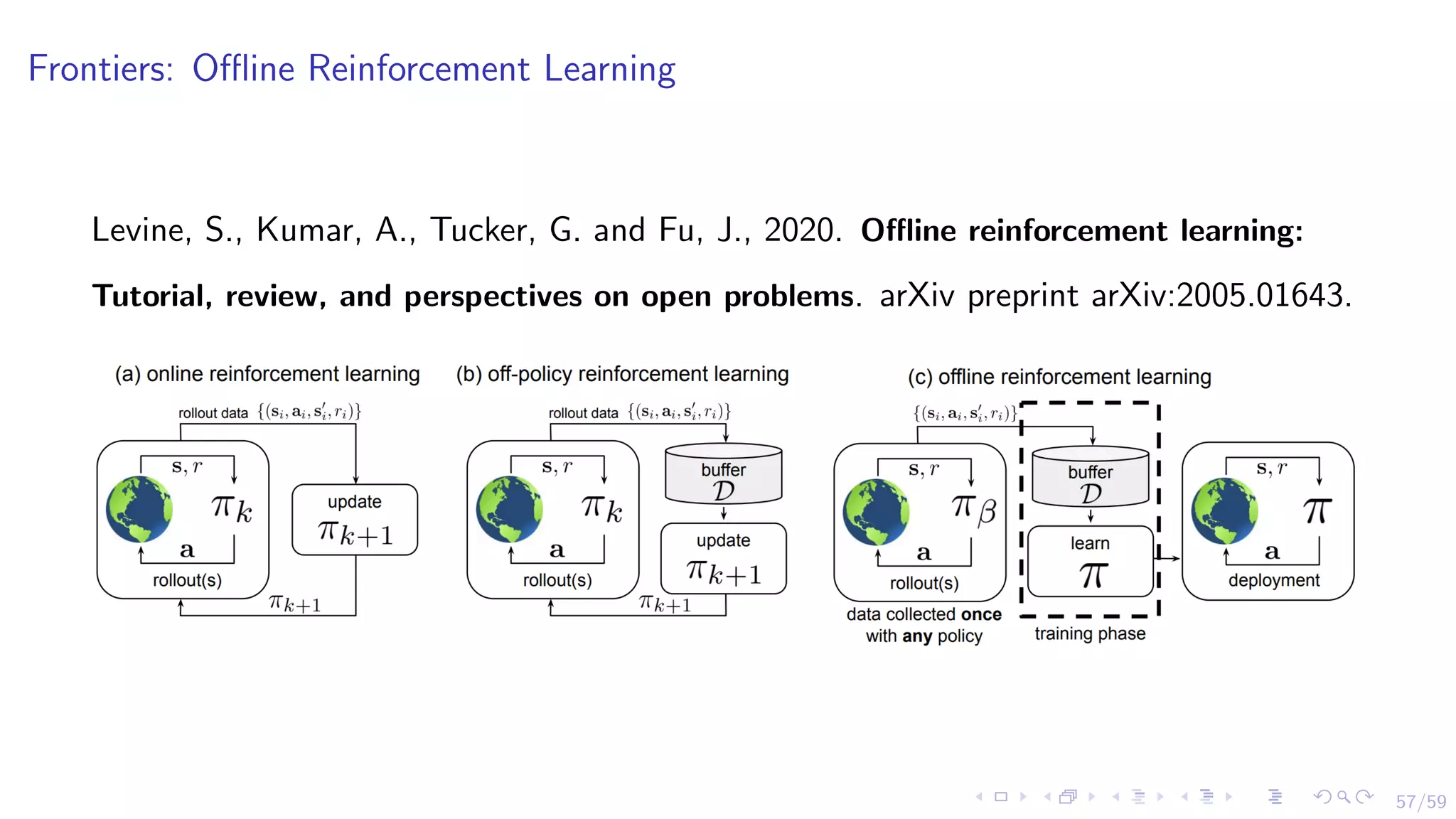
The document discusses the application of reinforcement learning (RL) in financial markets, detailing its advantages, key algorithms, and challenges. It describes RL as a sequential decision-making approach suitable for various trading objectives, such as proprietary trading and portfolio management. The authors emphasize the importance of understanding the algorithms and methodologies behind RL while also acknowledging that the document is for informational purposes and not investment advice.

1. 1/59
Reinforcement Learning for Financial Markets
Mahmoud Mahfouz1,2
, and Prof. Danilo Mandic1
(1) Department of Electrical and Electronic Engineering, Imperial College London
(2) J.P. Morgan Artificial Intelligence Research
March, 2021

2. 2/59
Table of Contents
Overview
Reinforcement Learning: Introduction
Reinforcement Learning: Key Algorithms
Financial Markets: Overview
Reinforcement Learning for Financial Markets
Reinforcement Learning: Challenges and Frontiers

3. 3/59
This material was prepared for informational purposes by the Artificial Intelligence Research group of JPMorgan
Chase & Co and its affiliates (“J.P. Morgan”), and is not a product of the Research Department of J.P.
Morgan. J.P. Morgan makes no representation and warranty whatsoever and disclaims all liability, for the
completeness, accuracy or reliability of the information contained herein. This document is not intended as
investment research or investment advice, or a recommendation, offer or solicitation for the purchase or sale of
any security, financial instrument, financial product or service, or to be used in any way for evaluating the merits
of participating in any transaction, and shall not constitute a solicitation under any jurisdiction or to any person,
if such solicitation under such jurisdiction or to such person would be unlawful.

4. 4/59
Table of Contents
Overview
Reinforcement Learning: Introduction
Reinforcement Learning: Key Algorithms
Financial Markets: Overview
Reinforcement Learning for Financial Markets
Reinforcement Learning: Challenges and Frontiers

5. 5/59
Overview
I Trading is a sequential decision making problem.
I Many different objectives:
I Proprietary Trading
I Market Making
I Agency Trading
I Portfolio Management
I Reinforcement Learning (RL) is an attractive
learning paradigm for trading.
I RL has been applied for trading problems and is
used in practice.

6. 6/59
Resources: Books
I Sutton, R.S. and Barto, A.G., 2018. Reinforcement learning: An
introduction. MIT press.
I Wellman, M.P., 2011. Trading agents. Synthesis Lectures on
Artificial Intelligence and Machine Learning, 5(3), pp.1-107.
I Bouchaud, J.P., Bonart, J., Donier, J. and Gould, M., 2018. Trades,
quotes and prices: financial markets under the microscope.
Cambridge University Press.

7. 7/59
Resources: Papers (1/2)
I Watkins, C.J. and Dayan, P., 1992. Q-learning. Machine learning, 8(3-4), pp.279-292.
I Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, I., Wierstra, D. and
Riedmiller, M., 2013. Playing atari with deep reinforcement learning. arXiv preprint
arXiv:1312.5602.
I Silver, D., Lever, G., Heess, N., Degris, T., Wierstra, D. and Riedmiller, M., 2014,
January. Deterministic policy gradient algorithms. In International conference on
machine learning (pp. 387-395). PMLR.
I Lillicrap, T.P., Hunt, J.J., Pritzel, A., Heess, N., Erez, T., Tassa, Y., Silver, D. and
Wierstra, D., 2015. Continuous control with deep reinforcement learning. arXiv
preprint arXiv:1509.02971.
I Ha, D. and Schmidhuber, J., 2018. World models. arXiv preprint arXiv:1803.10122.

8. 8/59
Resources: Papers (2/2)
I Wei, H., Wang, Y., Mangu, L. and Decker, K., 2019. Model-based reinforcement
learning for predictions and control for limit order books. arXiv preprint
arXiv:1910.03743.
I Nevmyvaka, Y., Feng, Y. and Kearns, M., 2006, June. Reinforcement learning for
optimized trade execution. In Proceedings of the 23rd international conference on
Machine learning (pp. 673-680)
I Spooner, T., Fearnley, J., Savani, R. and Koukorinis, A., 2018. Market making via
reinforcement learning. arXiv preprint arXiv:1804.04216.
I Filos, A., 2019. Reinforcement learning for portfolio management. arXiv preprint
arXiv:1909.09571.

9. 9/59
Resources: Code
I OpenAI Gym: A toolkit for developing and comparing reinforcement learning algorithms.
I stable-baselines: Implementations of reinforcement learning algorithms based on OpenAI
Gym.
I qtrader: Reinforcement Learning for Portfolio Management.
I rl-markets: Market making via reinforcement learning.
I abides: Agent-Based Interactive Discrete Event Simulation environment.

10. 10/59
Table of Contents
Overview
Reinforcement Learning: Introduction
Reinforcement Learning: Key Algorithms
Financial Markets: Overview
Reinforcement Learning for Financial Markets
Reinforcement Learning: Challenges and Frontiers

11. 11/59
Supervised vs Unsupervised vs Reinforcement Learning

12. 12/59
Reinforcement Learning (RL)
”Reinforcement learning is learning what to do - how to map situations to actions - so as to
maximize a numerical reward signal. The learner is not told which actions to take, but instead
must discover which actions yield the most reward by trying them.” Sutton, R.S. and Barto,
A.G., 2018

13. 13/59
The Agent-Environment Interface (1/2)

14. 14/59
The Agent-Environment Interface (2/2)
I The learner and decision maker is called the agent.
I The agent interacts with the environment which comprises everything outside the agent.
I At every step of interaction, the agent selects an action based on an observation emitted
by the environment.
I The environment is impacted by the action and changes giving rise to a new observation.
I The environment also gives rise to a reward, a special numerical value that the agent
seeks to maximize over time through its’ choice of actions
I Reinforcement learning attempts to make the agent learn optimal behaviors to achieve its
goal.

15. 15/59
State (1/2)
I The state St ∈ S is a representation of the environment and/or agent at time t. It is the
information the agent uses to determine the action to be taken.
I The state can be discrete S = {S1, S2, . . . , SN } or continuous S ⊆ RN
I The state can be decomposed to the environment state Se
t and the agent state Sa
t
I Se
t : the environment’s private representation
I Sa
t : the agent’s internal representation
I More formally, at each discrete time step t, the agent receives an observation Ot which
typically doesn’t fully characterize the state St
I Full observability: Ot = Se
t = Sa
t
I Partial observability: Se
t 6= Sa
t

16. 16/59
State (2/2)
I The history Ht is the sequences of observations, actions and rewards the agent receives.
Ht = O1, R1, A1, . . . , At−1, Ot, Rt (1)
I The agent state is a function of the history:
Sa
t = f(Ht) (2)
I Examples:
I inventory held (number of stocks) by the agent
I normalized stock price
I spread
I order volume imbalance

17. 17/59
Action
I The action At ∈ A is what the agent does at time t upon receiving information about the
environment and the reward it received.
I The action can be discrete At = {A1, A2, . . . , AM } or continuous A ⊆ RM
I Actions can have both short term and long term consequences.
I Examples:
I Discrete: market order or limit order
I Continuous: limit order + price + size

18. 18/59
Reward
I The reward Rt ∈ R at time t is a numerical (scalar) feedback signal the environment
emits based on the agent’s action and the state it was in and moved to.
I Rt = R(St, At, St+1), R : S × A × S → R
I The reward can be received instantaneously or is delayed.
I A key hypothesis in reinforcement learning is the Reward Hypothesis which states that
all goals can be described by the maximisation of expected cumulative reward.
I The return Gt is the total discounted (or undiscounted) reward starting from time step t
Gt = Rt+1 + γRt+2 + γ2
Rt+3 + . . . =
∞
X
k=0
γk
Rt+k+1 (3)
I γ ∈ [0, 1] is the discount factor representing the assigned present value of future rewards.
I Examples:
I PnL (profit and loss)
I Sharpe ratio

19. 19/59
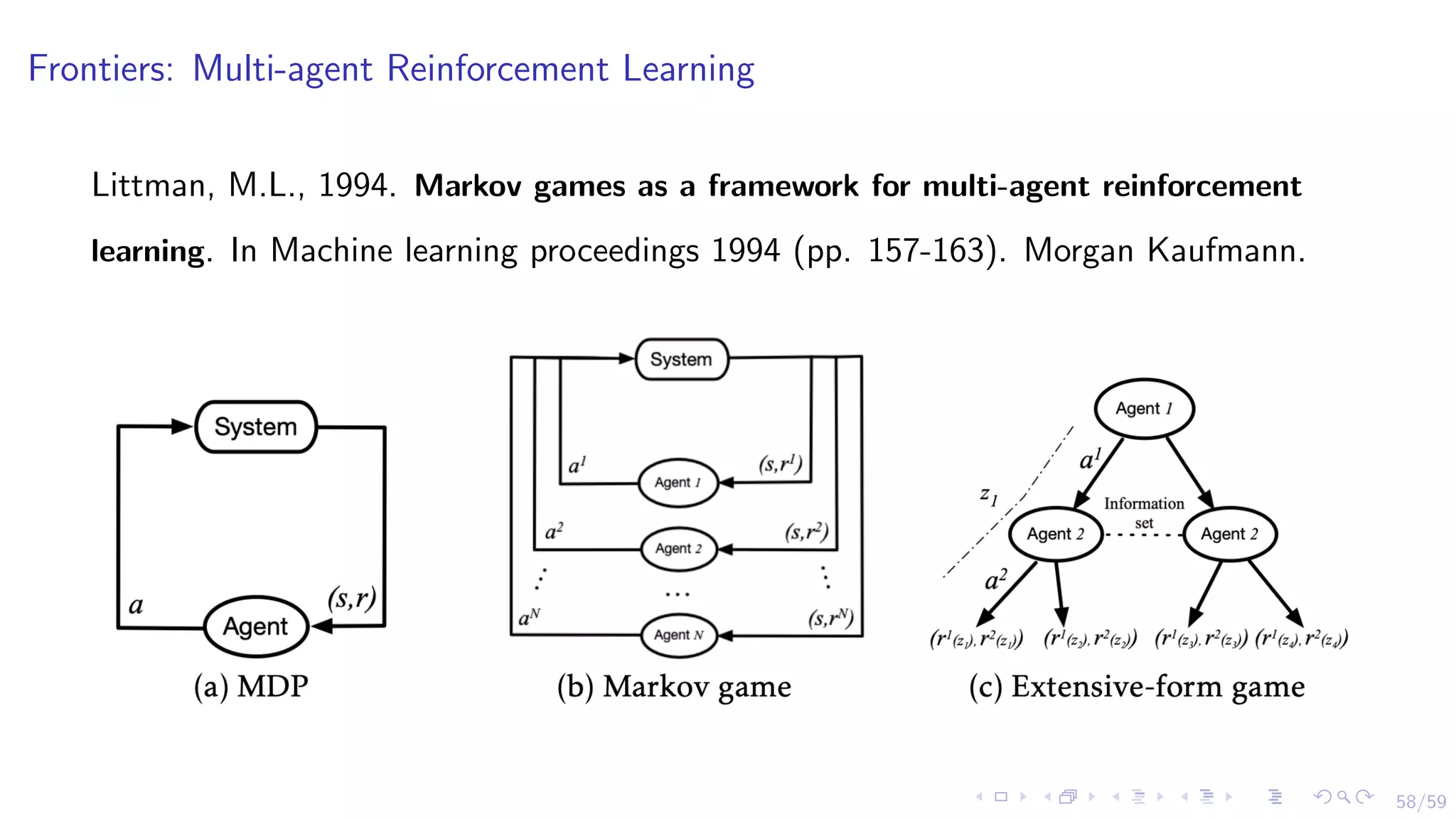
Markov Decision Process (1/3)
I Markov decision processes (MDP) describes a fully observable environment for the
reinforcement learning paradigm.
I Reinforcement Learning problems are typically formalised as an MDP.
I A key property is the Markov property:
P [St+1 | S1, . . . , St] = P [St+1 | St] (4)
I The state transition probability for a Markov state s and a successor state s0
is defined
by:
Pss0 = P [St+1 = s0
| St = s] (5)
I This can be defined in a matrix form with the state transition probability matrix P
describing the transition probabilities from all states s to all successor states s0
P =


P11 . . . P1n
.
.
.
Pn1 . . . Pnn

 (6)

20. 20/59
Markov Decision Process (2/3)
I A Markov Process (Markov Chain) is a tuple hS, Pi of random states S1, S2, . . . with
the Markov property.
I A Markov Reward Process is a tuple hS, P, R, γi
I A Markov Decision Process is an extension of the Markov reward process with decisions
in which all the states are Markov. It is a tuple hS, A, P, R, γi where,
I S is a finite set of states
I A is a finite set of actions
I P is a state transition probability matrix, Pa
ss0 = P [St+1 = s0
| St = s, At = a]
I R is a reward function, Ra
s = E [Rt+1 | St = s, At = a]
I γ is a discount factor, γ ∈ [0, 1]

21. 21/59
Markov Decision Process (3/3)
I Many extensions to MDP exist. These include, for example, Partially observable MDPs
I A Partially Observable Markov Decision Process is an extension of the Markov
decision process with hidden states. It is a tuple hS, A, O, P, R, Z, γi where,
I S is a finite set of states
I A is a finite set of actions
I O is a finite set of observations
I P is a state transition probability matrix, Pa
ss0 = P [St+1 = s0
| St = s, At = a]
I R is a reward function, Ra
s = E [Rt+1 | St = s, At = a]
I Z is an observation function, Za
s0o = P [Ot+1 = o | St+1 = s0
, At = a]
I γ is a discount factor, γ ∈ [0, 1]

22. 22/59
Policy
I The policy π is the function that fully defines the agent’s behaviour. The policy is
essentially what we’re trying to learn in reinforcement learning.
I A policy can be described as a mapping from state to actions π : S → A. More formally,
the policy π is a distribution over actions given states.
I It can be deterministic At+1 = π (St) or stochastic π(a | s) = P [At = a | St = s]
I Policies are stationary (time-independent), At+1 ∼ π (· | St) , ∀t > 0

23. 23/59
Value Function
I The value function is another important function that describes how good/bad it is to
be in a current state and/or taking a particular action. More formally, it is a prediction of
future rewards and gives the long-term value of the state s and action a.
I Remember, the return Gt is the total discounted reward starting from time step t
Gt = Rt+1 + γRt+2 + γ2
Rt+3 + . . . =
∞
X
k=0
γk
Rt+k+1 (7)
I The state-value function vπ(s) of an MDP is the expected return starting from state s,
and then following policy π
vπ(s) = Eπ [Gt | St = s] = Eπ
Rt+1 + γRt+2 + γ2
Rt+3 + . . . | St = s
(8)
I The action-value function qπ(s, a) of an MDP is the expected return starting from state
s, taking action a, and then following policy π
qπ(s, a) = Eπ [Gt | St = s, At = a] = Eπ
Rt+1 + γRt+2 + γ2
Rt+3 + . . . | St = s, At = a
(9)

24. 24/59
Bellman Expectation Equation
I The state-value function can be decomposed into two components: (1) the immediate
reward Rt+1 and (2) the discounted value of the successor state γvπ(St+1)
vπ(s) = Eπ [Gt | St = s]
= Eπ
Rt+1 + γRt+2 + γ2
Rt+3 + . . . | St = s
= Eπ [Rt+1 + γ (Rt+2 + γRt+3 + . . .) | St = s]
= Eπ [Rt+1 + γGt+1 | St = s]
= Eπ [Rt+1 + γvπ (St+1) | St = s]
(10)
I Similarly, the action-value function can be decomposed to:
qπ(s, a) = Eπ [Rt+1 + γqπ (St+1, At+1) | St = s, At = a] (11)

25. 25/59
Bellman Optimality Equations
I A policy π0
is defined to be better than or equal to a policy π if and only if
vπ0 (s) ≥ vπ(s), ∀s
I The optimal state-value function v∗(s) is the maximum state-value function over all
policies
v∗(s) = max
π
vπ(s) (12)
I The optimal action-value function v∗(s) is the maximum action-value function over all
policies
q∗(s, a) = max
π
qπ(s, a) (13)
I An optimal policy can be found by maximising over q∗(s, a)
π∗(a | s) =
(
1 if a = argmax
a∈A
q∗(s, a)
0 otherwise
(14)

26. 26/59
Value Function Approximation (1/2)
I Value function approximation is essential when
dealing with large MDPs with too many states and
actions.
I Function approximation is used to estimate the
value function and generalise from seen states to
unseen states
v̂(s, w) ≈ vπ(s) (15)
q̂(s, a, w) ≈ qπ(s, a) (16)
I Many function approximators exist and are used in
practice. These include using linear combination of
features, decision trees, nearest neighbour methods,
etc. The most widely used method for function
approximation is by using neural networks.

27. 27/59
Value Function Approximation (2/2)
I Linear Value Function Approximation: This represents the value function by a linear
combination of features.
v̂(S, w) = x(S)
w =
n
X
j=1
xj(S)wj (17)
J(w) = Eπ
h
vπ(S) − x(S)
w
2
i
(18)
∇wv̂(S, w) = x(S)
∆w = α (vπ(S) − v̂(S, w)) x(S)
(19)
I Function approximation using neural networks will be covered later in the lecture.

28. 28/59
Final Notes
I Reinforcement Learning vs Planning: RL deals with
problems where the environment is unknown initially. In
planning the environment dynamics are known and the agent
is able to improve it’s policy by querying the model of the
environment.
I Model-free vs Model-based Reinforcement Learning:
Model-free methods are used when the model of the
environment is unknown. Model-based methods rely on
having (or learning) the model and doing planning with this
model.
I Prediction vs Control: Predicition is concerned with
evaluating the future rewards given a certain policy. Control
is around optimising the future rewards by finding the best
policy.
I Exploration vs Exploitation: This is a key problem in
Reinforcement Learning. Should the learner focus on
exploration and finding more information about the
environment or focus on exploitation and using the known
information to maximise the future rewards?

29. 29/59
Table of Contents
Overview
Reinforcement Learning: Introduction
Reinforcement Learning: Key Algorithms
Financial Markets: Overview
Reinforcement Learning for Financial Markets
Reinforcement Learning: Challenges and Frontiers

30. 30/59
Overview

31. 31/59
-Greedy Exploration
I In Reinforcement Learning, it is important to balance between exploration and
exploitation.
I A common method for achieving that is using -greedy policy improvement.
I Given a choice between n actions:
π(a | s) =
(
/n + 1 − if a∗
= argmax
a∈A
Q(s, a)
/n otherwise
(20)
I The value is typically decayed throughout the learning process to encourage more
exploitation once the agent has explored enough at the beginning.

32. 32/59
On-policy vs Off-policy
I On-policy methods (left figure) attempt to evaluate or improve the policy that is used to
make decisions.
I In contrast, off-policy methods (right figure) evaluate or improve a policy different from
that used to generate the data.

33. 33/59
SARSA: On-policy Control
I SARSA (state-action-reward-state-action)
is an on-policy control algorithm.
I It is an on-policy algorithm because it
updates its Q-values using the Q-value of
the next state S0
and the current policy’s
action A0
.
I It estimates the return for the state action
pairs assuming the current policy
continues to be followed.
I Q(S, A) ←
Q(S, A) + α (R + γQ (S0
, A0
) − Q(S, A))
I Can use 1-step returns or n-step returns.
I SARSA is guaranteed to converge to the
optimal action-value function (under
certain assumptions).

34. 34/59
Q-Learning: Off-policy Control
I Q-Learning is off-policy because it updates its Q-values using the Q-value of the next
state S0
and the greedy action A0
. It estimates the returns for state-action pairs
assuming a greedy policy was followed despite the fact it is not following a greedy policy.
I In Q-Learning, we have two policies that are improving over time.
I Behaviour policy: At+1 ∼ µ (· | St) used
to select the next action.
I Target policy: A0
∼ π (· | St) that
considers alternative successor actions.
R + γQ (S0
, A0
)
=R + γQ
S0
, argmax
a
Q (S0
, a)
=R + γ max
a
Q (S0
, a)
(21)
I Q(S, A) ← Q(S, A) +
α (R + γ maxa Q (S0
, a) − Q(S, A))
I Q-Learning is also guaranteed to converge.

35. 35/59
DQN: Deep Q-Learning with Experience Replay
I Experience Replay: A buffer of transitions
I A deep Q-network is a neural network that
approximates the Q-value for an input
state-action pair.
I It is optimized by minimizing the square
error between the predicted and target
Q-value
L(θ) = E
h
(Q(s, a; θ) − Q)
2
i
Q = r + γQ (s0
, arg max Q (s0
, a0
; θ) ; θ)
(22)

36. 36/59
Policy Gradient
I Policy gradient methods attempt to learn
a parameterised policy directly instead of
generating the policy from the value
function (e.g. using -greedy)
πθ(s, a) = P[a | s, θ] (23)
I The goal is to find the best parameters θ
that maximizes J(θ)
I Policy gradient methods search for a local
maximum in J(θ) by ascending the
gradient of the policy w.r.t to θ
∆θ = α∇θJ(θ) (24)
I Policy Gradient Theorem:
∇θJ(θ) = Eπθ
[∇θ log πθ(s, a)Qπθ
(s, a)]
(25)

37. 37/59
Deep Deterministic Policy Gradient (DDPG)
I DDPG is an algorithm which concurrently
learns a Q-function (critic) and a policy
(actor).
I It uses off-policy data and the Bellman
equation to learn the Q-function, and uses
the Q-function to learn the policy.
I DDPG can only be used for environments
with continuous action spaces and can be
thought of as being deep Q-learning for
continuous action spaces.

38. 38/59
Table of Contents
Overview
Reinforcement Learning: Introduction
Reinforcement Learning: Key Algorithms
Financial Markets: Overview
Reinforcement Learning for Financial Markets
Reinforcement Learning: Challenges and Frontiers

39. 39/59
Overview (1/2)
Investing vs trading:
I Investing: buying holding a portfolio of instruments with an eye on the long-term value
of the investment
I Trading: making money through speculation on the price movement of instruments
Financial instruments:
I Cash: instruments whose value is determined directly by the market
I Derivatives: instruments which derive their value from the value of one or more
underlying entities
Instruments by asset class:
I Equities: stock, equity futures, stock options, exotic derivatives
I Indices: sector, strategy, fixed income, volatility
I FX: spot foreign exchange, currency futures, FX options, swaps
I Fixed Income: T-bills, deposits, interest rate futures, FRAs (forward rate agreements),
bonds, bond futures, interest rate swaps, options, caps/floors exotics
I ETFs: stock, index, bond, commodity, currency
I Commodities: metals, energy, livestock meat, agricultural
I Cryptocurrencies

40. 40/59
Overview (2/2)
Sell side vs Buy side:
I Sell side: The side which deals with the
creation, promotion and selling of
financial instruments to the public. These
include Investment banks, commercial
banks, stock brokers and market makers.
I Buy side: The side which makes the
investments in the market for the purpose
of money or fund management. These
include Hedge funds, asset managers,
institutional investors and retail investors

41. 41/59
Trading in the Financial Markets: Proprietary Trading
I Proprietary trading is a form of trading based on informed speculation about the
movement of asset prices.
I Proprietary trading firms trade with their own money as opposed to depositors’ money in
order to make profits for themselves.
I A variety of strategies are typically used such as fundamental analysis, global macro and
different forms of arbitrage.
I The introduction of the Volcker rule (a U.S. regulation) restricted banks from carrying out
proprietary trading due to conflicts of interest between banks and their customers.
I Most successful proprietary trading firms are highly technology-driven, utilizing complex
quantitative models and algorithms.

42. 42/59
Trading in the Financial Markets: Market Making
I Market Making is a key function carried out by banks for providing liquidity in the markets.
I Liquidity is the degree to which an asset can be quickly bought or sold in the market
without affecting the asset’s price (market impact).
I Market makers participate in the market by providing liquidity as both buyers and sellers
of one or more assets.
I By providing short-term liquidity, market makers make money by capturing the difference
between the bid and ask prices.
I Market makers need to control inventory and adverse price movement risks.
I Market Makers typically carry out extensive price and volume time series modelling and
their strategies are very sensitive to market microstructure.
I Some of the questions they address: how much liquidity to supply? What price? What
market venues/trading strategies to use? What margins to use? How to hedge?

43. 43/59
Trading in the Financial Markets: Agency Trading (1/2)
I Agency trading is a service provided to clients such
as pension funds aiming to buy/sell large quantities
of a given financial asset.
I Makes money through the commission the client
pays to the agency trader.
I Executing a big order in one go is a bad idea!
I Agency trading strategies slice and dice the order
across time and venues to balance the urgency and
risk requirements of their clients.
I Some of the questions they address: how to
minimize market impact/transactions
costs/slippage? How to schedule trades over time?
Where to place the orders? What price? How to
route trades between venues?

44. 44/59
Trading in the Financial Markets: Agency Trading (2/2)
I Time Weighted Average Price (TWAP): Time weighted average price strategy breaks
up a large order and releases dynamically determined smaller chunks of the order to the
market using evenly divided time slots between a start and end time. The aim is to
execute the order close to the average price between the start and end times, thereby
minimizing market impact.
I Volume Weighted Average Price (VWAP) Strategies: Breaks up a large order and
releases dynamically determined smaller chunks of the order to the market using stock
specific historical volume profiles. The aim is to execute the order close to the Volume
Weighted Average Price (VWAP), thereby benefiting on average price.
I Percentage of Volume (POV) Strategies: Until the trade order is fully filled, this
algorithm continues sending partial orders, according to the defined participation ratio and
according to the volume traded in the markets. The related ”steps strategy” sends orders
at a user-defined percentage of market volumes and increases or decreases this
participation rate when the stock price reaches user-defined levels.

45. 45/59
Trading in the Financial Markets: Typical Hedge Fund Strategies
I Long/Short equity: Long buy assets that are expected to outperform, sell short assets
that are expected to under-perform
I Long-only or short-only
I Market Neutral: Similar to long-short but attempt to minimize or eliminate the impact
of market volatility on the performance
I Delta Neutral: combination of options and its underlying security, where trades are
placed to offset positive and negative deltas (a ratio comparing the change in the price of
an asset to the corresponding change in the price of its derivative) so that the portfolio
delta is maintained at zero.
I Global Macro: Trade in almost all assets by making macroeconomic bets and searching
for global opportunities. Invest in situations created by changes in government policy,
economic policies and interest rates. Macro funds tend to use derivatives and can be
highly leveraged.
I Emerging Markets
I Arbitrage

46. 46/59
Trading Venues
I Markets, nowadays, are fragmented and decentralized.
I Different asset classes trade differently:
I Exchange-traded: standardized financial instruments that are traded on an
organized exchange
I Over-the-counter: traded off an exchange, customized pricing, maturity, quantity
and frequency
I Electronic communication networks: automated systems matching buy and sell orders
for securities. These connect major brokerages and individual traders so they can trade
directly between themselves without going through a middleman.
I Dark Pools: private stock exchanges designed for trading large blocks of securities away
from the public eye. They are called ”dark” because of their complete lack of
transparency, which benefits the big players but may leave the retail investor at a
disadvantage. It also introduces an inefficiency in the market as exchange prices no longer
reflect the real market.
I Internalization: occurs when a broker decides to fill the client’s order from the inventory
of stocks the brokerage firm owns.

47. 47/59
Limit Order Book (1/4)
I The order book is an electronic list of buy
and sell limit orders for a specific financial
instrument organised by price levels.
I A matching engine is used to match
incoming orders and determine which
orders can be fulfilled.
I Orders are first ranked according to their
price. Orders of the same price are then
ranked depending on when they were
entered (price-time priority).

48. 48/59
Limit Order Book (2/4)

49. 49/59
Limit Order Book (3/4)
Main order types:
I Market order:
I Buy/Sell X amounts of an instrument at the
best available price.
I Cannot be amended or cancelled during
market hours.
I Limit order:
I Set a maximum purchase price for a buy
orders, or a minimum sale price for sell orders.
I If the market doesn’t reach the limit price, the
order will not be executed.

50. 50/59
Limit Order Book (4/4)
I An order book snapshot in time xt can be formalised into:
xt =
pi
a(t), vi
a(t), pi
b(t), vi
b(t)
n
i=1
(26)
I where, pi
a(t), pi
b(t) are the ask and bid prices respectively for price level i and vi
a(t), vi
b(t)
are the ask and bid volumes respectively for price level i.
I the mid price is equal to
p1
a(t)+p1
b(t)
2
I the spread is equal to p1
a(t) − p1
b(t)
I the order volume imbalance is equal to
v1
a(t)−v1
b (t)
v1
a(t)+v1
b (t)

51. 51/59
Table of Contents
Overview
Reinforcement Learning: Introduction
Reinforcement Learning: Key Algorithms
Financial Markets: Overview
Reinforcement Learning for Financial Markets
Reinforcement Learning: Challenges and Frontiers

52. 52/59
Reinforcement learning for optimized trade execution
I Nevmyvaka, Y., Feng, Y. and Kearns, M., 2006, June. Reinforcement learning for
optimized trade execution. In Proceedings of the 23rd international conference on
Machine learning (pp. 673-680).
I States: elapsed time, remaining inventory, bid-ask spread and bid-ask volume imbalance
I Actions: limit order with a price relative to the best bid or ask
I Reward Function: slippage
I Algorithm: Q-Learning + Dynamic Programming

53. 53/59
Market Making via reinforcement learning
I Spooner, T., Fearnley, J., Savani, R. and Koukorinis, A., 2018. Market making via
reinforcement learning. arXiv preprint arXiv:1804.04216.
I States: (1) agent-state: inventory, active quoting distances, (2) market state: bid-ask
spread, mid-price move, order volume imbalance, signed volume, volatility and relative
strength index
I Actions: (1) simultaneous buy and sell limit orders with different spreads, (2) market
order to clear inventory
I Reward Function: (1) PnL, (2) PnL + Inventory
I Algorithm: Q-Learning, SARSA and R-learning + variants

54. 54/59
Model-based reinforcement learning for predictions and control for limit order books
I Wei, H., Wang, Y., Mangu, L. and
Decker, K., 2019. Model-based
reinforcement learning for predictions
and control for limit order books. arXiv
preprint arXiv:1910.03743.
I States: latent representation of the Limit
order book, trade prints and trading
agent’s position
I Actions: buy/sell quantity
I Reward Function: mark-to-market PnL
I Algorithm: World Model + Double
DQN, Policy Gradient and A2C

55. 55/59
Table of Contents
Overview
Reinforcement Learning: Introduction
Reinforcement Learning: Key Algorithms
Financial Markets: Overview
Reinforcement Learning for Financial Markets
Reinforcement Learning: Challenges and Frontiers

56. 56/59
Challenges
I Financial Markets are not MDPs - more like POMDPs
I Developing an accurate simulator of financial markets is almost impossible!
I Non-stationarity of financial time series.
I Interpretability of deep learning-based function approximators.
I Reinforcement Learning methods are extremely sample-inefficient!

57. 57/59
Frontiers: Offline Reinforcement Learning
Levine, S., Kumar, A., Tucker, G. and Fu, J., 2020. Offline reinforcement learning:
Tutorial, review, and perspectives on open problems. arXiv preprint arXiv:2005.01643.

58. 58/59
Frontiers: Multi-agent Reinforcement Learning
Littman, M.L., 1994. Markov games as a framework for multi-agent reinforcement
learning. In Machine learning proceedings 1994 (pp. 157-163). Morgan Kaufmann.

59. 59/59
Frontiers: Evolution Strategies
Salimans, T., Ho, J., Chen, X., Sidor, S. and Sutskever, I., 2017. Evolution strategies
as a scalable alternative to reinforcement learning. arXiv preprint arXiv:1703.03864.