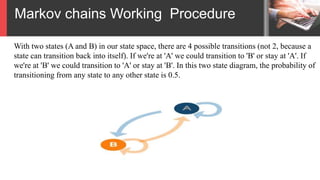
This presentation introduces Markov models. A Markov model is a stochastic method that models randomly changing systems based on transitions between states, where the probability of moving to the next state depends only on the current state, not on past states. There are four main types of Markov models: Markov chains, hidden Markov models, Markov decision processes, and partially observable Markov decision processes. Markov chains work by defining a set of possible states and the transition probabilities between states, such that the probability of moving from the current state to the next state can be determined.

1. WELCOME TO MY PRESENTATION
Markov Model
Supervise By
Md. Nazmus Sakib
Lecturer
Department OF CSE
WUB
Submitted By
Abdul momin
ID:WUB/15/32/1197
Dept: CSE

2. What is Markov Model?
01
02
A Markov model is a stochastic method for randomly
changing systems where it is assumed that future states do not
depend on past states. These models show all possible states as
well as the transitions, rate of transitions
and probabilities between them.
It moves from current state to Next state according to the
transition probabilities associated with the Current state
This kind of system is called Finite or Discrete Markov model.
03

3. Type of Markov Model
01
02 Hidden Markov model - used by systems that are autonomous
where the state is partially observable.
Markov decision processes - used by controlled systems
with a fully observable state
03
There are four types of Markov models that
are used situational
Markov chain - used by systems that are autonomous
and have fully observable states
04
Partially observable Markov decision processes - used by controlled
systems where the state is partially observable.

4. Markov property
• Markov Property : The Current state of the system depends only on the previous state of the sys
tem
• The State of the system at Time [ T+1 ] depends on the state of the system at time T.
Xt=1
Xt=2 Xt=3 Xt=4 Xt=5

5. Markov chains Working Procedure
Markov chains, named after Andrey Markov, are mathematical systems that
hop from one "state" (a situation or set of values) to another. For example, if
you made a Markov chain model of a baby's behavior, you might include "
playing," "eating", "sleeping," and "crying" as states, which together with
other behaviors could form a 'state space': a list of all possible states. In
addition, on top of the state space, a Markov chain tells you the probability
of hopping, or "transitioning," from one state to any other state e.g., the
chance that a baby currently playing will fall asleep in the next five minutes
without crying first.

6. Markov chains Working Procedure
With two states (A and B) in our state space, there are 4 possible transitions (not 2, because a
state can transition back into itself). If we're at 'A' we could transition to 'B' or stay at 'A'. If
we're at 'B' we could transition to 'A' or stay at 'B'. In this two state diagram, the probability of
transitioning from any state to any other state is 0.5.

7. Reference
https://en.wikipedia.org/wiki/Markov_model
http://whatis.techtarget.com/definition/Markov-model

9. Thank you