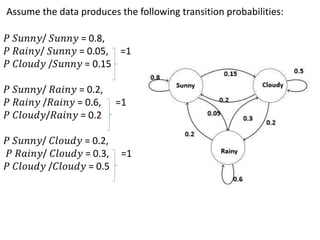
This document discusses different types of Markov models including Markov chains, hidden Markov models, and Markov decision processes. It provides examples of using a Markov chain to model weather predictions based on historical data and transition probabilities. Markov chains can model systems where states change randomly over time and are useful for applications such as data analysis, physics, chemistry, medicine, population processes, and detecting weather conditions. Markov decision processes extend Markov chains to model controlled systems and are used in fields like robotics, economics, and networking.

1. SUBHABRATA MAITY
MBT/10004/17

2. INTRODUCTION
- Markov Process are proposed by Russian
Mathematician , Andery Markov.
- In probability theory, a Markov model is a
stochastic model randomly changing system.

3. - There are four common
Markov Models.
System state
is fully
observable
System state is partially
observable
System is
autonom
ous
Markov Chain Hidden Markov Model
System is
controlle
d
Markov
decision
process
Partially observable
Markov decision process

4. MARKOV CHAIN
- It is a simplest Markov Model.
- It models the state of a system with a
random variable that changes through time.
- A Markov chain can be described by a
transition matrix.
-

5. TRANSITION MATRIX
- It is also termed as probability
matrix or Markov matrix or
substitution matrix.
- It is a square Matrix used to describe
the transitions of a Markov chain.

6. -Design a Markov Chain to predict
the weather of tomorrow using
previous information of the past days.
-Our model has only 3 states: 𝑆 = 𝑆1,
𝑆2, 𝑆3 , and the name of each state is
𝑆1 = 𝑆𝑢𝑛𝑛𝑦 , 𝑆2 = 𝑅𝑎𝑖𝑛𝑦, 𝑆3 = 𝐶𝑙𝑜𝑢𝑑
𝑦.
-To establish the transition
probabilities relationship between
states we will need to collect data.
EXAMPLE OF MARKOV CHAIN

7. Assume the data produces the following transition probabilities:
𝑃 𝑆𝑢𝑛𝑛𝑦/ 𝑆𝑢𝑛𝑛𝑦 = 0.8,
𝑃 𝑅𝑎𝑖𝑛𝑦/ 𝑆𝑢𝑛𝑛𝑦 = 0.05, =1
𝑃 𝐶𝑙𝑜𝑢𝑑𝑦 /𝑆𝑢𝑛𝑛𝑦 = 0.15
𝑃 𝑆𝑢𝑛𝑛𝑦/ 𝑅𝑎𝑖𝑛𝑦 = 0.2,
𝑃 𝑅𝑎𝑖𝑛𝑦 /𝑅𝑎𝑖𝑛𝑦 = 0.6, =1
𝑃 𝐶𝑙𝑜𝑢𝑑𝑦/𝑅𝑎𝑖𝑛𝑦 = 0.2
𝑃 𝑆𝑢𝑛𝑛𝑦/ 𝐶𝑙𝑜𝑢𝑑𝑦 = 0.2,
𝑃 𝑅𝑎𝑖𝑛𝑦/ 𝐶𝑙𝑜𝑢𝑑𝑦 = 0.3, =1
𝑃 𝐶𝑙𝑜𝑢𝑑𝑦 /𝐶𝑙𝑜𝑢𝑑𝑦 = 0.5

8. - Let’s say we have a sequence: Sunny, Rainy,
Cloudy, Cloudy, Sunny, Sunny, Sunny, Rainy,
….; so, in a day we can be in any of the three
states.
- We can use the following state sequence
notation: 𝑞1, 𝑞2, 𝑞3, 𝑞4, 𝑞5,….., where 𝑞𝑖 𝜖 {
𝑆𝑢𝑛𝑛𝑦,𝑅𝑎𝑖𝑛𝑦,𝐶𝑙𝑜𝑢𝑑𝑦}.
-In order to compute the probability of
tomorrow’s weather we can use the Markov
property:
𝑃 (𝑞1,…,𝑞𝑛) = 𝑃(𝑞𝑖|𝑞𝑖−1) 𝑖=1

9. APPLICATION OF MARKOV CHAIN MODEL
-It can be used for data analysis.
- It is used in various study field
such as physics, chemistry,
medicine, music etc.
- It is used in thermodynamics
and statistical mechanics.
- Markov chain methods have also become very
important for generating sequences of random
numbers via process called Markov Chain Monte
Carlo(MCMC).

10. -It is used in mathematical Biology , specially in
population processes.
- Markov chains can be used in
population genetics.
- It is used to detect weather condition .

11. MARKOV DECISION PROCESS
-A Markov decision process is a discrete time stochastic
control process .
- It is an extension of Markov chain model.
-It is applied in case of when system is controlled and
system state is fully observable.
- Markov decision processes (MDPs) provide a mathematical
framework for modeling decision making in situations
where outcomes are partly random and partly under the
control of a decision marker.

12. APPLICATIONS OF MARKOV DECISION PROCESS
-It is used in various field such as robotics, automatic
control, economics, manufacturing etc.
- It is used in network (world wide web) process.