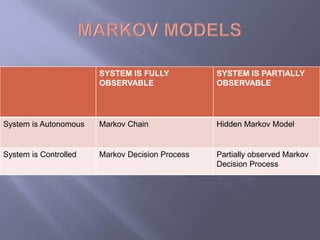
This document defines operations research as using scientific methods and advanced analytical techniques to help make better decisions, especially regarding allocation of scarce resources. It discusses several applications of operations research including scheduling airlines and facility placement. Key operations research techniques are described like linear programming, simulation, and queuing theory. The document also defines Markov processes and Markov chains, explaining that Markov models assume the Markov property that future states only depend on the present state. It contrasts Markov chains with hidden Markov models and discusses how Monte Carlo simulation and Markov chain Monte Carlo methods are used for sampling from probability distributions.

1. Markov Model and
Monte Carlo Model
10/21/2014 By : Eng. Sajid Ali 1

2. Definition :
“Operation Research is defined as
a scientific approach to decision making
which seeks to determine how best to
design and operate a system under
conditions requiring the allocation of scarce
resources”
According to Prof G. Srinivasan

3. “Operation Research is a discipline that
deals with the application of advanced
analytical methods to help make better
decisions”
“Operations Research provides a set of
algorithms that acts as tools for effective
problem solving and decision making”

4.  Scheduling airlines, including both planes and crew.
 Deciding the appropriate place to site new facilities
such as a warehouse, factory or fire station.
 Managing the flow of water from reservoirs.
 Identifying possible future development paths for parts
of the telecommunications industry.
 Establishing the information needs and appropriate
systems to supply them within the health service.
 Identifying and understanding the strategies adopted
by companies for their information systems.

5.  Linear Programming - Formulations
 Linear Programming – Solutions
 Duality and Sensitivity Analysis
 Transportation Problem
 Assignment Problem
 Dynamic Programming
 Deterministic Inventory Models

6.  Simulation
 Mathematical Optimization
 Queuing Theory
 Stochastic-Process Models
 Markov Decision Processes
 Decision Analysis
 Linear Programming

7. A Markov process is a stochastic process
(random process) in which the probability
distribution of the current state is conditionally
independent of the path of past states, a
characteristic called the Markov property.
Markov chain is a discrete-time stochastic
process with the Markov property.
Stochastic Process :-
“ In probability theory a stochastic process is a
collection of random variables representing the
evolution of some system of random values over time.”

8. A stochastic process has the Markov property if
the conditional property distribution of future
states of the process (conditional on both past
and present values) depends only upon the
present state, and the future does not depend
upon the past or not on the sequence of events
that preceded it. A process with this property is
called a Markov process.

9.  Andrey Markov produced the first results
(1906) for these processes purely theoretically.
 In 1917 practical application was made
by Erlang to obtain formulas for call loss and
waiting time in telephone networks.

10. A Markov model is stochastic model that assumes
Markov property. A stochastic model models a
process where the state depends on previous
states in a non-deterministic way.

11. SYSTEM IS FULLY
OBSERVABLE
SYSTEM IS PARTIALLY
OBSERVABLE
System is Autonomous Markov Chain Hidden Markov Model
System is Controlled Markov Decision Process Partially observed Markov
Decision Process

12. The simplest Markov model is the Markov Chain.
It models the state of a system with a random
variable that changes through time.
The distribution for this variable depends only on
the distribution of the previous state.
Example : Markov Chain Monte Carlo
Random Variable :
In probability and statistics, a random variable or stochastic
variable is a variable whose value is subject to variations due
to chance.

13. Markov Hidden Model is Markov chain in which
the state is only partially observable. Like
observations are related to state of the system but
they are insufficient to determine the state.
Well known algorithms of Markov Hidden Model
exists likewise
 Viterbi Algorithms
 Forward Algorithms
 Baum-Welch Algorithms

14. Monte Carlo started as a gambling place
around 1950. The most famous casino known
as Monte Carlo but it soon became a technical
term for simulation of random processes.
It’s a sample from distribution and to compute
maximum mean.
Markov Chain Monte Carlo soon inverted after
ordinary Monte Carlo in 1953 at Los Alamos.
Geyer in 1992 and Tierney in 1994 firstly
started doing work on MCMC.

15. In Statistics , Markov Chain Monte Carlo (
MCMC) methods are a class of algorithms
for sampling from a Probability distribution.
Its also said to be sampling using the local
information.
The quality of the sample improves as a
function of the number of steps.
probability distribution is a probability to each measurable subset of the
possible outcomes of a random experiment

16. MCMC methods are primarily used for
calculating numerical approximation of multi-dimensional
integrations , for example in
Bayesian statistics,.
 They are also used for generating samples that
gradually populate the rare failure region
in rare event sampling.
 MCMC is generic problem solving technique.
 Basically used for optimization and decision
making.
sampling is concerned with the selection of a subset of individuals
from within a statistical population to estimate characteristics of the
whole population