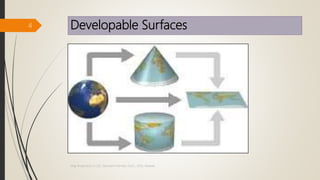
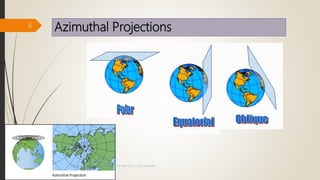
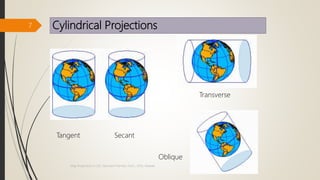
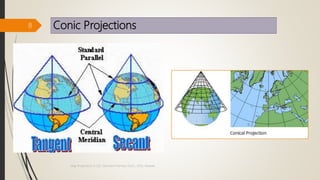
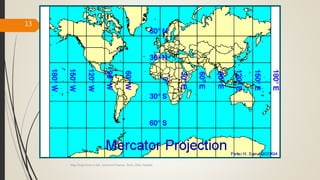
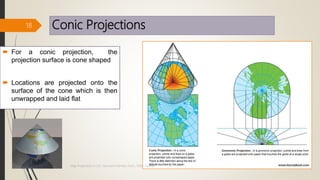
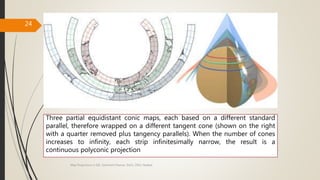
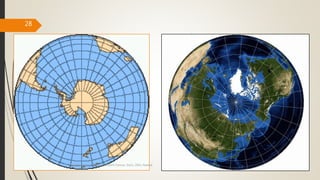
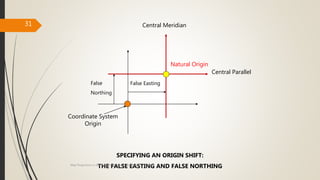
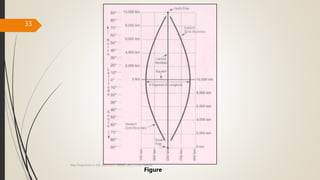
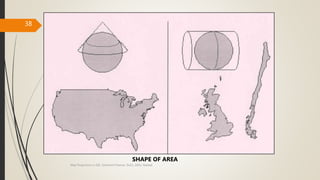
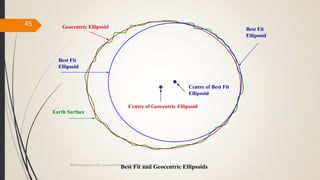
The document provides an overview of map projections in GIS, detailing their classification based on extrinsic and intrinsic properties, including cylindrical, conic, and azimuthal projections. It discusses the characteristics, advantages, and limitations of several specific projections such as Mercator, Transverse Mercator, and Lambert Conformal Conic. The importance of selecting the appropriate projection for accurate geographic representation and the implications for GIS applications is emphasized.