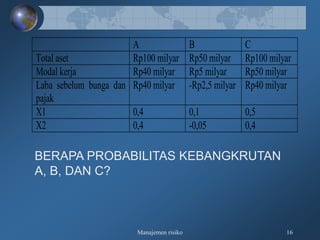
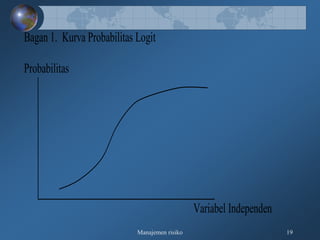
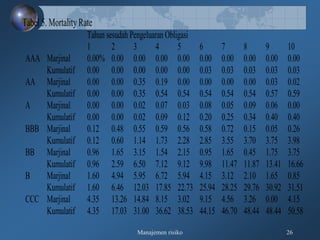
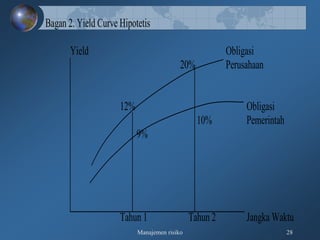
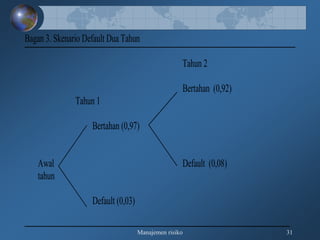
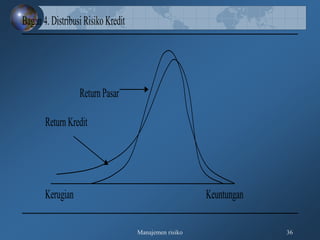
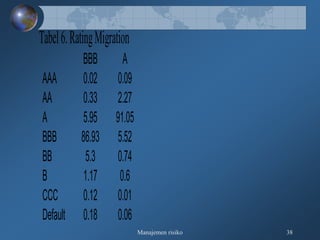
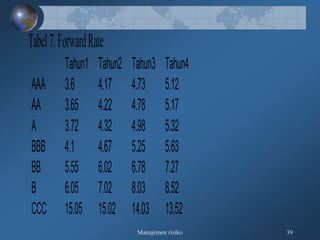
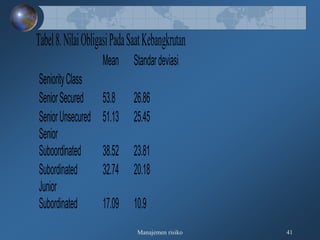
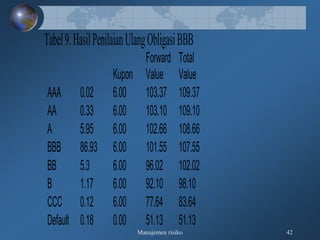
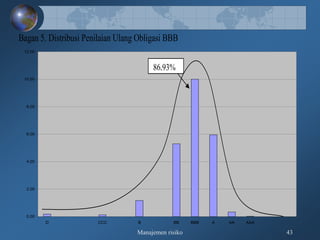
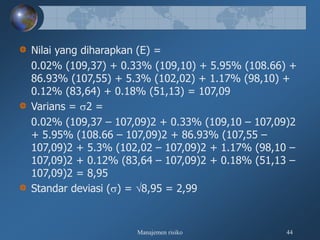
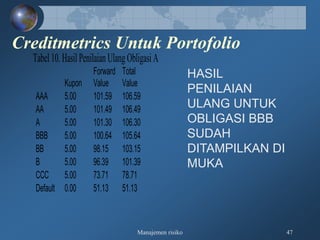
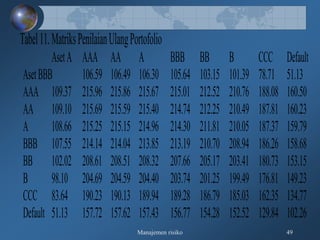
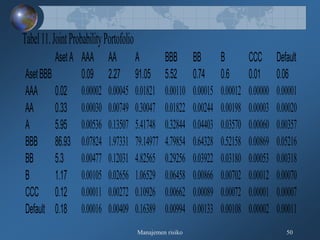
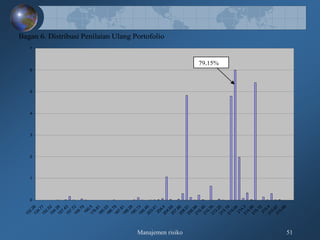
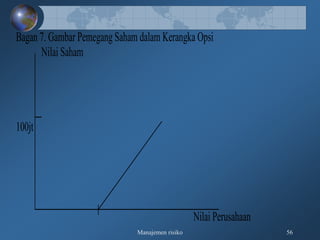
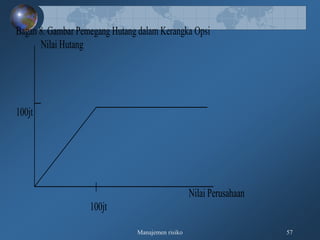
Dokumen tersebut membahas tentang pengukuran risiko kredit secara kualitatif dan kuantitatif, meliputi kerangka 3R dan 5C untuk penilaian kualitatif, serta teknik-teknik pengukuran kuantitatif seperti rating perusahaan, model skoring kredit, RAROC, dan creditmetrics."