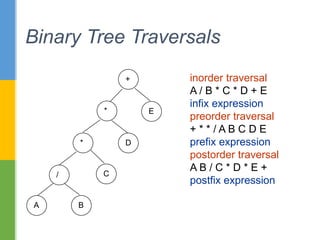
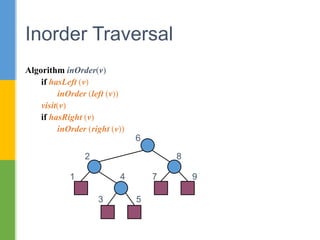
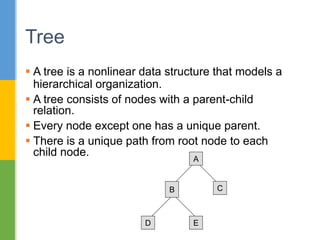
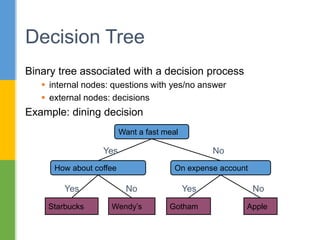
The document discusses trees as a nonlinear data structure with nodes connected in a parent-child relationship. It provides examples of different types of trees including binary trees, binary expression trees, and decision trees. Binary trees are defined recursively with each node having at most two children. The document also covers different methods of representing trees including sequentially and linked, as well as tree traversal algorithms including inorder, preorder and postorder traversal.

1. Presented by:
Mubashar Mehmood
Implementation of
Trees

2.  A tree is a nonlinear data structure that models a
hierarchical organization.
 A tree consists of nodes with a parent-child
relation.
 Every node except one has a unique parent.
 There is a unique path from root node to each
child node.
Tree
A
B
D E
C

3. List Tree
Start head root
# before 1 (prev) 1 (parent)
# after 1 (next) >= 1 (children)
Comparison of Tree and List

4. Binary tree associated with an arithmetic expression
 internal nodes: operators
 external nodes: operands
Example: arithmetic expression tree for the expression
(2  (a - 1) + (3  b))
Arithmetic Expression Tree
+

-2
a 1
3 b

5. Binary tree associated with a decision process
 internal nodes: questions with yes/no answer
 external nodes: decisions
Example: dining decision
Decision Tree
Want a fast meal
How about coffee On expense account
Starbucks Wendy’s Gotham Apple
Yes No
Yes No Yes No

6.  A special class of trees: max degree for each node is
2.
 Recursive definition: A binary tree is a finite set of
nodes that is either empty or consists of a root and
two disjoint binary trees called the left subtree and the
right subtree.
Binary Trees
B
E
H I

7. Sequential Representation
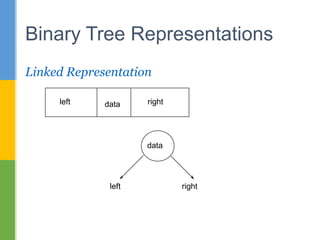
Binary Tree Representations
A
B
E
C
D
A
B
--
C
--
--
--
D
--
.
E
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
.
[16]
(1) waste space
(2) insertion/deletion
problem
A
B
C
D
E
F
G
H
I
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
A
B C
GE
I
D
H
F

8. Linked Representation
Binary Tree Representations
dataleft right
left right
data

9. • Let L, V, and R stand for moving left, visiting
the node, and moving right.
• There are six possible combinations of traversal
• lRr, lrR, Rlr, Rrl, rRl, rlR
• Adopt convention that we traverse left before
right, only 3 traversals remain
• lRr, lrR, Rlr
• inorder, postorder, preorder
Binary Tree Traversals

10. Binary Tree Traversals
+
*
A
*
/
E
D
C
B
inorder traversal
A / B * C * D + E
infix expression
preorder traversal
+ * * / A B C D E
prefix expression
postorder traversal
A B / C * D * E +
postfix expression

11. Inorder Traversal
3
1
2
5
7 9
8
4
6
Algorithm inOrder(v)
if hasLeft (v)
inOrder (left (v))
visit(v)
if hasRight (v)
inOrder (right (v))