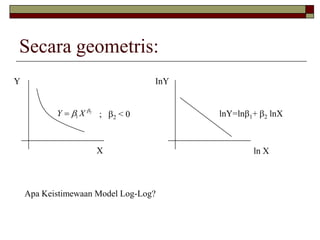
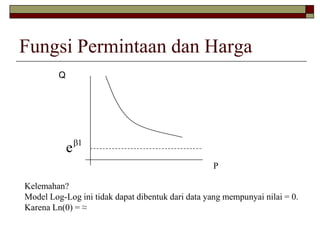
Dokumen ini membahas berbagai bentuk model regresi untuk menganalisis hubungan antara harga dan permintaan gula pasir, serta kelebihan dan kekurangan dari model linier, log-log, semi-log, dan reciprocal. Ditegaskan bahwa model log-log dapat memberikan nilai elastisitas yang lebih informatif dibandingkan model linier, serta penerapan model semi-log dan reciprocal dalam konteks pertumbuhan dan biaya tetap. Model-model ini juga memiliki batasan dalam hal prediksi ketika harga mencapai nol dan memperlihatkan perilaku konsumsi berdasarkan perubahan pendapatan.

1. BENTUK-BENTUK FUNGSIONAL DARI MODEL REGRESI

2. Pendahuluan
Persamaan model linier:
Y = b1+ b2X + u ;
dimana:
X menyatakan harga gula pasir per Kg
Y menyatakan kuantitas yang diminta.
Berapa permintaan jika harga gula pasir = 0 rupiah?
Apa mungkin suatu komoditi berharga 0 rupiah?
Apa logis bila harga gula pasir per Kg = 0, maka permintaan hanya sebesar b1?.
Untuk mengatasi kelemahan tersebut, maka akan dipelajari model yang merupakan bentuk-bentuk fungsional dari model regresi.

3. Jenis Model Fungsional
Model Log-Log
Model Semi Log
Model Reciprocal
Kurva Philips
Kurva Engel

4. Model log-log
 Model ini juga dikenal dengan: Model Double Log dan Model Konstan
Elastisitas
 Menurut suatu teori ekonomi, hubungan antara kuantitas yang diminta dan
harga suatu komoditas mempunyai bentuk sebagai berikut:
Y X eu   
1
2 Y : kuantitas
X : harga
1, 2 : parameter-parameter
u : error
Model diatas mirip dengan Fungsi Produksi (Model Cobb Douglas)
Model tidak linier baik variabel  Sulit diestimasi
Untuk mempermudah, model ditransformasi

5. Hasil transformasi logaritma:
lnY = ln 1+ 2ln X + u
Transformasi dilakukan pada dua sisi Model Log-Log
Redefinisi Model :
Y* = 1* + 2* X* + u*
Dimana:
Y*= ln Y
X*= ln X
1*= ln 1
2*= 2
u*= u
Redefinisi model menunjukkan bahwa model sesungguhnya merupakan model regresi linier1* dan 2* dapat ditaksir dengan OLS.

6. Secara geometris:
Y   X 
1
2 ; 2 < 0
ln X
Y
X
InY
lnY=ln1+ 2 lnX
Apa Keistimewaan Model Log-Log?

7. Keistimewaan Model Log-Log dibandingkan dengan Model Linier:
Slope 2dalam Model Log-Log menyatakan elastisitas Y terhadap X, yaitu ukuran persentasi perubahan dalam Y bila diketahui perubahan persentasi X. Dengan perkataan lain, bila Y menyatakan kuantitas yang diminta dan X menyatakan harga komoditas per unit, maka 2menyatakan elastistas harga dari permintaan.
1dan 2 juga bisa diinterpretasikan dengan mengembalikan model ke bentuk semula. Jadi, 1dan 2di interpretasikan melalui e1dan e2. Model tersebut juga menunjukan bahwa bila harga komoditi mahal sekali, maka permintaan akan minimal, yaitu e1, dan bila harga murah sekali, maka permintaan maksimal.
Harga tidak akan pernah mencapai nilai nol. Sehingga dapat dikatakan bahwa permasalahan yang dihadapi dalam regresi linier dapat teratasi dengan fungsi ini.

8. Fungsi Permintaan dan Harga
Q
1 e
P
Kelemahan?
Model Log-Log ini tidak dapat dibentuk dari data yang mempunyai nilai = 0.
Karena Ln(0) = ≈

9. Ilustrasi Masalah
Perhatikan dua model yang menyatakan hubungan antara harga gula pasir (X) dengan banyaknya gula pasir yang dikonsumsi (Y).
Fungsi linier:
Y = 2,6911 –0,4795 X
SE : (0,1216) (0,1140)
R2= 0,6628
Model Log-Log:
ln Y = 0,774 –0,2530 ln
SE : (0,0152) (0,0494)
R2 = 0,7448
Manakah model yang paling cocok?.

10. Analisis
Lihat R2.Apakah model log-log lebih baik ?.
Data aktual dan hasil transformasi tidak dapat dibandingkan karena skala besaran yang digunakan berbeda.
Slop dan intercept kedua bentuk model berbeda. Interpretasinya:.
Model linier
Bila harga gula pasir naik sebesar 1 unit, maka permintaan terhadap komoditi tersebut akan turun ½ unit.
Model log-log
Setiap kenaikan harga gula pasir sebesar 1%, jumlah yang diminta akan turun 0,25 %.Atau dapat dikatakan, elastisitas harga = -0,25.
Komoditi Elastis atau tidak? Berapa batasan elastis?

11. Analisis
Komoditas ini tidak elastis karena perubahan harga gulapasir tidak menimbulkan gejolak yang besar terhadap permintaannya.
Dalam Prakteknya:
Model Log-Log dibuat karena sebarandata mengikuti garis tersebut.
Adanya permasalahan dalam membuat regresi linier

12. Model Semi-log
Prinsip model sama dengan model log-log, yaitu melakukan transformasi logaritma terhadap data. Bedanya, pada model semi-log data yang ditransformasi hanya salah satu dari Y atau X.
Model Semi Log terdiri atas dua jenis model, yaitu:
Model Log-Lin
Model Lin-Log

13. Model Log-Lin
ln Y = 1 + 2 X + u
Interpretasi:
2 merupakan rasio antara perubahan relatif Y terhadap perubahan absolut
X, dituliskan sebagai berikut :
perubahan _ absolut _ dalam _X
perubahan _ relatif _ dalam _Y
2  
Penggunaan:
Variabel X menyatakan unit waktu (tahun, bulan, dan seterusnya)
Y dapat menyatakan pengangguran, penduduk, keuntungan, penjualan,
GNP, dan sebagainya.
Oleh karena itu, 2 merupakan suatu ukuran pertumbuhan (growth rate)
bila 2 > 0 atau merupakan suatu ukuran penyusutan (decay) bila 2 < 0.
Oleh karenanya, model ini disebut juga model pertumbuhan.

14. Ilustrasi
Berdasarkan data pertumbuhan Produk Nasional Bruto (PNB) atas dasar harga konstan (pertumbuhan riil) tahun 1986 –2004 di suatu negara, diperoleh model:
ln PNB = 6,9636 + 0,0796 Tahun
SE : (0,0151) (0,0017)
R2= 0,9756
Analisis?
Model tersebut menyatakan bahwa 2= 0,0796. Artinya, setiap tahunnya PNB naik/tumbuh 7,96 % pada periode 1986 –2004.

15. Model Lin-Log
Y = 1 + 2 ln X + u
Interpretasi:
2 merupakan ukuran rasio antara perubahan absolut Y terhadap
perubahan relatif X, dituliskan sebagai berikut :
2 
perubahan absolut dalam Y
perubahan relatif dalam X
_ _ _
_ _ _
Digunakan pada situasi dimana perubahan relatif pada X akan mengakibatkan
perubahan absolut pada Y.
Misal: Perusahaan mempunyai target omset, maka kita dapat melihat kenaikan
keuntungan.

16. Ilustrasi
Perhatikan Model yang menunjukkan hubungan antara laba dan omset:
Laba = 1040,1105 + 24,9879 Ln Omset
SE : (18,8574) (2,0740)
R2= 0,9236
Interpretasi: Setiap Omset naik 1% maka laba akan naik sebesar 24 juta rupiah.
Bagaimana jika perusahaan menargetkan tahun depan omset naik 5%?

17. Model Reciprocal
Sifat: apabila X bernilai sangat besar, maka Y akan memiliki harga mendekati 1.
Yxu    121

18. Aplikasi I (1 > 0, 2 > 0) : Model
Rata-rata Biaya Tetap Suatu Kelas
Didefinisikan :
Y : Rata-rata biaya tetap
X : Banyaknya mahasiswa/kelas
 Biaya operasional yang diperlukan dapat dikategorikan menjadi dua jenis,
yaitu :
 Biaya tetap, meliputi: sewa ruangan, honor dosen, dan lain-lain.
 Biaya variabel, meliputi: makan, snack, hand-out, dan lain-lain.
 Hubungan antara Y dan X dapat dinyatakan sebagai:
Y
x
  u

 

 
   1 2
1
; 1 > 0, 2 > 0

19. Fungsi reciprocal untuk 1> 0, dan 2> 0
Karakteristik model :
Pada saat jumlah mahasiswa tidak banyak (X kecil), rata-rata biaya tetap sangat besar. Kebalikannya, bila jumlah mahasiswa sangat banyak (X besar sekali), rata-rata biaya tetap mendekati 1(1> 0).
Cara mengestimasi model?
OLS (Ordinary Least Square)
1
YX

20. Aplikasi II (1< 0, 2> 0)
Didefinisikan :
X: tingkat pengangguran (%)
Y: tingkat perubahan upah (%)
Bentuk hubungan antara Y dan X digambarkan dalam kurva berikut : Tingkat Pengangguran Alami
Y
X
-1Kurva Philips

21. Ilustrasi
Kurva Phillips: United Kingdom, 1950-1966
Y = -1,4282 + 8,7243
t: (2,0625) (2,8498)
R2= 0,3849
Pengamatan :
1= -1,43 %Artinya?
Batas bawah perubahan upah –1,43 %. Artinya, bila unemployment rate (tingkat pengangguran) besar sekali, penurunan upah tidak lebih dari 1,43 % per tahun
R2sangat rendah, kurang dari 40 %, tetapi intercep dan slop keduanya signifikan.

22. Aplikasi III (1> 0, 2< 0)
Didefinisikan :
Y : konsumsi / pengeluaran pada suatu komoditas
X : pendapatan
Hubungan antara pendapatan seseorang dengan konsumsi suatu komoditas digambarkan dalam Kurva Engel :

23. Sifat:
 Ada garis ambang pendapatan (threshold level of income ). Bila
pendapatan lebih kecil dari garis ambang pendapatan, komoditas tersebut
tidak akan dibeli/dikonsumsi (-2/1).
 Ada suatu level kejenuhan. Meskipun pendapatan mencapai level sangat
tinggi, konsumsi komoditas tidak akan melewati level tersebut (1).
Y
x
  u

 

 
   1 2
1
-2/1
C
I
1




x
1