This document provides an overview of linear programming, including its history, key components, assumptions, and applications. Linear programming involves maximizing or minimizing a linear objective function subject to linear constraints. It was developed in 1947 and can be used to optimize problems involving allocation of limited resources. The key components of a linear programming problem are the objective function, decision variables, constraints, and parameters. It makes assumptions of proportionality, additivity, continuity, determinism, and finite choices. Common applications of linear programming include production planning, facility location, and transportation problems.

1. Compiled by Tsegay Berhe MSc in Production Engineering and Management 1
Linear Programming: Model Formulation and Graphical solution method
Linear Programming – An overview
Model Formulation
Characteristics of Linear Programming Problems
Assumptions of a Linear Programming Model
Advantages and Limitations of a Linear Programming.
A Maximization Model Example
Graphical Solutions of Linear Programming Models
A Minimization Model Example
Introduction
A branch of applied mathematics, which is a mathematical technique that involves maximizing
and minimizing a linear functions subject given to linear constraints is called linear
programming (developed by George Dantzig in 1947). The term “linear” refers to the
relationship involving two or more variables which show first- degree mathematical statement.
The term “programming” refers to the use of certain mathematical techniques or algorithms to
obtain best possible or the optimal solution.
A large number of decision problems faced by a manager involve allocation of resources to
various activities, with the objective of increasing profit, or decreasing cost. Normally, the
resources are scarce (= limited) and the performance of a number of activities within the
constraints (= limitations) of limited resources is a challenge. A manager is, therefore required
to decide as to how best to allocate resources among the various activities.
One of the major applications of linear algebra involving systems of linear equations is in
finding the maximum or minimum of some quantity, such as profit or cost. In mathematics the
process of finding an extreme value (maximum or minimum) of a quantity (normally called a
function) is known as optimization.
The linear programming method is a popular mathematical technique used to choose the best
alternative from a set of feasible alternatives in situations in which the objective function as well
as the constraints can be expressed as linear mathematical functions. Linear Programming is a
mathematical modeling technique used to determine a level of operational activity in order to
achieve an objective.
Additionally, Linear programming (LP) can be defined as a branch of Mathematics which deals
with modeling a decision problem and subsequently solving it by mathematical techniques. The
problem is presented in a form of a linear function which is to be optimized (i.e. maximized or
minimized) subject to a set of linear constraints. The function to be optimized is known as the
objective function.

2. Compiled by Tsegay Berhe MSc in Production Engineering and Management 2
The general linear programming problem calls for optimizing (maximizing / minimizing) a
linear function of variables called the „objective function’, subject to a set of linear equations
and / or inequalities called the „constraints‟, or „restrictions.
Mathematical programming is used to find the best or optimal solution to a problem that
requires a decision or set of decisions about how best to use a set of limited resources to achieve
a state goal of objectives.
History of linear programming
It started in 1947 when G. B. Dantzig designed the “simplex method” for solving linear
programming formulations of U.S. Air Force planning problems.
It soon became clear that a surprisingly wide range of apparently unrelated problems in
production management could be stated in linear programming terms and solved by the simplex
method.
Requirements for application of linear programming
 The aim or object should be clearly identifiable and definable in mathematical terms.
Example: Maximization of profit, Minimization of cost, Minimization of time etc.
 The activities involved should be distinct and measurable in quantitative terms. Example:
How many products of a particular type should be made in a time period? How many
waiters are to be employed during a time period? Etc.
 The resources to be allocated should be measurable quantitatively.
Example: The availability of material (in kgs), the availability of machine time (in
hours); the availability of labour (in man-hours), the demand for a product in the market
(in units, liters) etc.
 The relationships representing the objective function and the constraints must be linear
in nature.
 There should be a series of feasible alternative courses of action available to the decision
maker, which is determined by the resource constraints.
Assumptions Underlying Linear Programming
A. Proportionality; A primary requirement of a linear programming problem is that the
objective function and every constraint function must be linear. As an example, if 1 kg of
a product costs Rs 2, then 10 kg will cost Rs 20. Similarly, if a steel mill can produce
200 tons in an hour, it can produce 1000 tons in 5 hours. This assumption, thus, ignores
bulk discounts and idle times‟

3. Compiled by Tsegay Berhe MSc in Production Engineering and Management 3
B. Additivity; Additivity indicates that the total of all activities is given by the sum total of
each activity conducted separately. For example, if it takes T1 hours on machine G to
make a unit of product A and T2 hours to make a unit of product B, then time required
on machine G to produce X1 units of A and X2 units of product B is T1X1 + T2X2. Thus,
the time required to change the set up on the machine from product A to product B is
neglected.
C. Continuity; It is assumed that the decision variables are continuous. As a consequence,
combinations of output with fractional values (especially in the context of production
problems) are possible. For example, the solution to an LP problem might yield a
solution X1 = 2.54 tones; X2 = 3.18 tones etc. Normally, we deal with integer values, but
even fractional values are permissible.
D. Deterministic; various parameters, namely the objective function coefficients and the
coefficients of the variables in the constraints are known with certainty. Hence, linear
programming is deterministic in nature.
E. Finite Choices; A linear programming model also assumes that a limited number of
choices are available to the decision maker.
Applications of Linear Programming
The following are the various applications of LP problems in productions:
Production;
 Product Mix and product proportioning;
 Production planning;
 Assembly line balancing;
 Oil refining; (5) Paper trimming;
 Hospital scheduling;
 Agricultural operations
Linear Programming Models
Linear programming models are mathematical representations of constrained optimization
problems. These models have certain characteristics in common. Knowledge of these
characteristics enables us to recognize problems that can be solved using linear programming.
In addition, it also can help us formulate LP models. The characteristics can be grouped into
two categories: components and assumptions. First, let‟s consider the components. Four
components provide the structure of a linear programming model:
a. Objective.
b. Decision variables.
c. Constraints.
d. Parameters

4. Compiled by Tsegay Berhe MSc in Production Engineering and Management 4
Linear programming algorithms require that a single goal or objective, such as the maximization
of profits, be specified. The two general types of objectives are maximization and minimization.
A maximization objective might involve profits, revenues, efficiency, or rate of return.
Conversely, a minimization objective might involve cost, time, distance travelled, or scrap.
a. Objective function; The objective function is a mathematical expression that can be used to
determine the total profit (or cost, etc., depending on the objective) for a given solution.
b. Decision variables represent choices available to the decision maker in terms of amounts of
either inputs or outputs. For example, some problems require choosing a combination of
inputs to minimize total costs, while others require selecting a combination of outputs to
maximize profits or revenues.
c. Constraints: Constraints are inequalities (such as machine time, availability of materials,
market demand etc.) representing restrictions on the value of the objective function. These
constraints have to be written in the linear form. Constraints are limitations that restrict the
alternatives available to decision makers. The three types of constraints are less than or
equal to (≤), greater than or equal to (≥), and simply equal to (═). A ≤constraint implies an
upper limit on the amount of some scarce resource (e.g., machine hours, labour hours,
materials) available for use. A ≥ constraint specifies a minimum that must be achieved in the
final solution (e.g., must contain at least 10 percent real fruit juice, must get at least 30 km/L
on the highway). The ═ constraint is more restrictive in the sense that it specifies exactly
what a decision variable should equal (e.g., make 200 units of product A).
d. Non-Negativity Constraints: Since the decision variables cannot take negative values
(except in the case of certain unrestricted variables), the non-negative constraints have to be
incorporated in the LP problem.
e. Parameters; An LP model consists of a mathematical statement of the objective and a
mathematical statement of each constraint. These statements consist of symbols (e.g., X1, X2)
that represent the decision variables and numerical values, called parameters. The
parameters are fixed values; the model is solved given those values.
A linear programming model can consist of one or more constraints. The constraints of a
given problem define the set of all feasible combinations of decision variables; this set is
referred to as the feasible solution space. Linear programming algorithms are designed to
search the feasible solution space for the combination of decision variables that will yield an
optimum in terms of the objective function.
Linear programming finds many uses in the business and industry, where a decision maker
may want to utilize limited available resources in the best possible manner. The limited
resources may include material, money, manpower, space and time. Linear Programming
provides various methods of solving such problems. In this unit, we present the basic
concepts of linear programming problems, their formulation and methods of solution.

5. Compiled by Tsegay Berhe MSc in Production Engineering and Management 5
Linear Programming Model Formulation
Mathematically, the general linear programming problem (LPP) may be stated as:
( ) ∑
{
( )
( )
( )
( )
 The function Z is the objective function.
 X1, X2, . . ., Xn are the decision variables.
 The expression (≤ = ≥) means that each constraint may take any one of the three
signs.
 Cj (j = 1, . . ., n) represents the per unit cost or profit to the jth variable.
 bi (i = 1, . . ., m) is the requirement or availability of the ith constraint.
 X1, X2, . . ., Xn ≥ 0 is the set of non-negative restriction on the LPP. In real life
problems negative decision variables have no valid meaning.
In this module we shall only discuss cases in which the constraints are strictly inequalities
(either have a ≤ or ≥). In formulating the LPP as a mathematical model we shall follow the
following four steps.
Step 1. Identify the decision variables and assign symbols to them (e.g. X, Y, Z, . . . OR
X1, X2, X2, . . .). These decision variables are those quantities whose values we wish to
determine.
Step 2. Identify the set if constraints and express them in terms of inequalities involving
the decision variables.
Step 3. Identify the objective function and express it is terms of the decision variables.
Step 4. Add the non-negativity condition.
Example 1
Elixir paints produces both interior and exterior paints from two raw materials M1 and M2. The
following table provides the data.
Raw material
Tons of raw material per ton of Maximum daily
Exterior paint Interior paint availability (in tons)
M1 6 4 24
M2 1 2 6
Profit in thousands 5 4

6. Compiled by Tsegay Berhe MSc in Production Engineering and Management 6
of birr per ton
The market survey restricts the market daily demand of interior paints to 2 tons. Additionally, the
daily demand for interior paints cannot exceed that of exterior paints by more than 1 ton.
Formulate the LPP.
Solution:
The general procedure for formulation of an LPP is as follows
 To identify and name the decision variables. That is to find out the variables of
significance and what is to be ultimately determined. In this example the quantity (In
tons) of exterior (EP) and interior paints (IP) to be produced under the given constraints
to maximize the total profit is to be found. Therefore, the EP and IP are the decision
variables. The decision variables EP and IP can be assigned name such as EP = X1 and
IP =X2.
 To the frame the objective equation. Our objective is to maximize the profits by
producing the right quantity of EP and IP. For every ton of EP produced a profit birr
5000 and for every ton of IP a profit of birr 4000 is made. This is indicated as 5 and 4 in
table 1 as profit in thousands of birrs. We can use the values of 5 and 4 in our objective
equation and later multiply by a factor 1000 in the final answer.
Therefore, the objective equation is framed as ;
Where X1 and X2 represent the quantities (in tons) of EP and IP to be produced.
 To identify the constraints and frame the constraint equations
In the problem statement there are constraints relating to the raw materials used and
there are constraints relating to the demand for the exterior and interior paints. Let us
first examine the raw material constraints. There are two types of raw materials used
namely
M1 and M2. The maximum availability of M1 every day is given as 24 tons and the
problem (refer table 1.1) states that 6 tons of M1 is required for producing 1 ton of
exterior paint. Now the quantity of exterior paint to be produced is denoted as x1, so if 6
tons of M1 is required for producing 1 ton of exterior paint, to produce x1 tons of
exterior paint (6 * x1) tons of M1 is required. Similarly, the problem states that 4 tons of
M1 is required for producing 1 ton of interior paint. Now the quantity of interior paint to
be produced is denoted as x2, so if 4 tons of M1 is required for producing 1 ton of
interior paint, to produce x2 tons of exterior paint (4 * x2) tons of M1 is required. But the
total quantity of M1 used for producing x1 quantity of exterior paint and x2 quantity of
interior paint cannot exceed 24 tons (since that is the maximum availability). Therefore,
the constraint equation can be written as;
In the same way the constraint equation for the raw material M2 can be framed. At this
point I would suggest that you must try to frame the constraint equation for raw material
M2 on your own and then look into the equation given in the text. To encourage you to
frame this equation on your own I am not exposing the equation now but am showing this
equation in the consolidated solution to the problem.

7. Compiled by Tsegay Berhe MSc in Production Engineering and Management 7
The problem states that the daily demand for interior paints is restricted to 2 tons. In
other words, a maximum of 2 tons of interior paint can be sold per day. If not more than
2 tons of interior paints can be sold in a day, it advisable to limit the production of
interior paints also to a maximum of 2 tons per day (I am sure you agree with me). Since
the quantity of interior paints produced is denoted by x2, the constraint is now written as;
The statement states that the daily demand for interior paints can be greater than the demand for
exterior paints but that difference cannot be more than 1 ton. Again, we can conclude that based
on demand it is advisable that if we produce interior paints more than exterior paints, that
difference in tons of production cannot exceed 1 ton. By now you are familiar that the quantities
of exterior paint and interior paint produced are denoted by X1 and X2 respectively. Therefore,
let us frame the constraint equation as the difference in the quantities of paints produced.
There is one more standard constraint known as the non-negativity constraint. The rationale
behind this constraint is that the quantities of exterior and interior paints produced can never be
less than zero. That is, it is not possible to produce negative quantity of any commodity.
Therefore, X1 and X2 must take values of greater than or equal to zero. This constraint is now
written as;
Thus, we have formulated (that is written in the form of equations) the given statement problem.
The consolidated formulation is given below.
The objective equation is;
Subjected to;
non negativity constraint
Example 2;
A company manufactures two products X and Y, which require, the following resources. The
resources are the capacities machine M1, M2, and M3. The available capacities are 50,25 and
15 hours respectively in the planning period. Product X requires 1 hour of machine M2 and 1
hour of machine M3. Product Y requires 2 hours of machine M1, 2 hours of machine M2 and 1
hour of machine M3. The profit contribution of products X and Y are ETB 5/unit and ETB 4/unit
respectively. Formulate the mathematical model / representation of this problem.
Solution
Tabular form;
Resource
Products Capacity
X Y
M1 2 50
M2 1 2 25

8. Compiled by Tsegay Berhe MSc in Production Engineering and Management 8
M3 1 1 15
Profit contribution 5 4
Decision variables
Let
X1 is the amount of X products produced
X2 is the amount of Y products produced
Objective equation
Subjected to;
Graphical Solution to A Linear Programming Problem
The graphical method of solving a linear programming problem is used when there are only two
decision variables. If the problem has three or more variables, the graphical method is not
suitable. In that case we use the simplex method which is discussed in the next section.
We begin by giving some important definitions and concepts that are used in the methods of
solving linear programming problems.
 Solution; A set of values of decision variables satisfying all the constraints of a linear
programming problem is called a solution to that problem.
 Feasible solution; Any solution which also satisfies the non-negativity restrictions of the
problem is called a feasible solution.
 Optimal feasible solution; Any feasible solution which maximizes or minimizes the
objective function is called an optimal feasible solution.
 Feasible region; The common region determined by all the constraints and non-
negativity restriction of a LPP is called a feasible region.
 Corner point; A corner point of a feasible region is a point in the feasible region that is
the intersection of two boundary lines.
If the optimal value of the objective function in a linear programming problem exists, then that
value must occur at one (or more) of the corner points of the feasible region.
To solve a linear programming problem with two decision variables using the graphical method
we use the procedure outlined below;
Graphical method [corner point /extreme approach] of solving a LPP
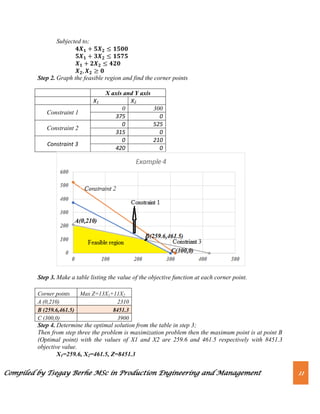
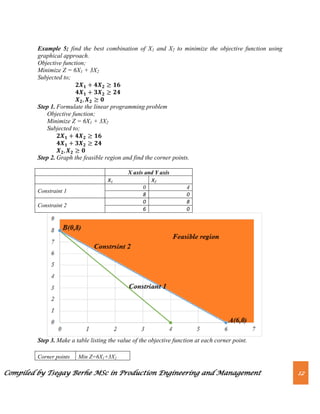
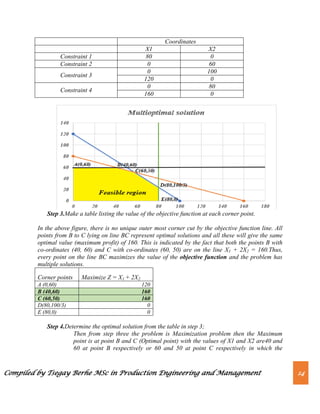
Step 1. Formulate the linear programming problem by writing the objective function
(generally maximize profit or Minimize cost) and the constraints.
Step 2. Plot the constraints on the graph and graph the feasible region and find the
corner points by changing the constraints into equalities.
Step 3. The coordinates of the corner points can be obtained by either inspection or by
solving the two equations of the lines intersecting at that point.

9. Compiled by Tsegay Berhe MSc in Production Engineering and Management 9
Step 4. Make a table listing the value of the objective function at each corner point/ Test
which point is most profitable.
Step 5. Determine the optimal solution from the table in step 3. If the problem is of
maximization (minimization) type, the solution corresponding to the largest (smallest)
value of the objective function is the optimal solution of the LPP.
Example 3
The Electro Comp Corporation manufactures two electrical products: air conditioners and large
fans. The assembly process for each is similar in that both require a certain amount of wiring
and drilling. Each air conditioner takes 3 hours of wiring and 2 hours of drilling. Each fan must
go through 2 hours of wiring and 1 hour of drilling. During the next production period, 240
hours of wiring time are available and up to 140 hours of drilling time may be used. Each air
conditioner sold yields a profit of $25. Each fan assembled may be sold for a $15 profit.
Formulate and solve this LP production mix situation to find the best combination of air
conditioners and fans that yields the highest profit. Use the corner point graphical approach.
Solution
Tabular form
Resource
Products
Hours available
Air conditioning(X1) Large fans(X2)
Wiring 3 2 240
Drilling 2 1 140
Profit contribution 25 15
Step 1. Formulate the linear programming problem
Let
X1 is the amount of Air conditioning products produced
X2 is the number of Large fans products produced
Objective equation
Subjected to;
Step 2. Graph the feasible region and find the corner points
 First find the X axis and Y axis of the constraints
X axis and Y axis
X1 X2
Constraint 1
0 120
80 0
Constraint 2 0 140

10. Compiled by Tsegay Berhe MSc in Production Engineering and Management 10
70 0
Then using the coordinates graph the constraint on the x and y axis
Step 3. Make a table listing the value of the objective function at each corner point.
Corner points Max Z=25X1+15X2
A (0,80) 1200
B (40,60) 1900
C (70,0) 1750
Step 4. Determine the optimal solution from the table in step 3;
Then from step three the problem is maximization problem then the maximum point is at
point B(optimal point ) with the values of X1 and X2 are 40 and 60 respectively with
2200 objective value.
X1=40, X2=60, Z=2200
Example 4; find the best combination of X1 and X2 to maximize the objective function using
graphical approach.
Subjected to;
Solution
Step 1. Formulate the linear programming problem

11. Compiled by Tsegay Berhe MSc in Production Engineering and Management 11
Subjected to;
Step 2. Graph the feasible region and find the corner points
X axis and Y axis
X1 X2
Constraint 1
0 300
375 0
Constraint 2
0 525
315 0
Constraint 3
0 210
420 0
Step 3. Make a table listing the value of the objective function at each corner point.
Corner points Max Z=13X1+11X2
A (0,210) 2310
B (259.6,461.5) 8451.3
C (300,0) 3900
Step 4. Determine the optimal solution from the table in step 3;
Then from step three the problem is maximization problem then the maximum point is at point B
(Optimal point) with the values of X1 and X2 are 259.6 and 461.5 respectively with 8451.3
objective value.
X1=259.6, X2=461.5, Z=8451.3

12. Compiled by Tsegay Berhe MSc in Production Engineering and Management 12
Example 5; find the best combination of X1 and X2 to minimize the objective function using
graphical approach.
Objective function;
Minimize Z = 6X1 + 3X2
Subjected to;
Step 1. Formulate the linear programming problem
Objective function;
Minimize Z = 6X1 + 3X2
Subjected to;
Step 2. Graph the feasible region and find the corner points.
X axis and Y axis
X1 X2
Constraint 1
0 4
8 0
Constraint 2
0 8
6 0
Step 3. Make a table listing the value of the objective function at each corner point.
Corner points Min Z=6X1+3X2

13. Compiled by Tsegay Berhe MSc in Production Engineering and Management 13
A (6,0) 36
B (0,8) 24
Step 4. Determine the optimal solution from the table in step 3;
Then from step three the problem is minimization problem then the minimum point is at point
B (Optimal point) with the values of X1 and X2 are 0 and 8 respectively in which the
objective value equals to 24.
X1=0, X2=8, Z=24
Special cases in graphical method
a) Multiple Optimal Solutions
b) Unbounded Solution
c) Infeasible Solution
a) Multiple Optimal Solutions; When the objective function passed through only the
extreme point located at the intersection of two half planes, then the linear programming
problem possess unique solutions. When the objective function coincides with one of the
half planes generated by the constraints in the problem, will possess multiple optimal
solutions.
The linear programming problems discussed in the previous section possessed unique
solutions. This was because the optimal value occurred at one of the extreme points
(corner points). But situations may arise, when the optimal solution obtained is not
unique. This case may arise when the line representing the objective function is parallel
to one of the lines bounding the feasible region. The presence of multiple solutions is
illustrated through the following example.
Example
Maximize Z = X1 + 2X2
subject to
X1 ≤ 80
X2 ≤ 60
5X1 + 6X2 ≤ 600
X1 + 2X2 ≤ 160
X1 ≥ 0; X2 ≥ 0
Solution
Step 1.Formulate the linear programming problem
Maximize Z = X1 + 2X2
subject to
X1 ≤ 80
X2 ≤ 60
5X1 + 6X2 ≤ 600
X1 + 2X2 ≤ 160
X1 ≥ 0; X2 ≥ 0
Step 2.Graph the feasible region and find the corner points.
Coordinates

14. Compiled by Tsegay Berhe MSc in Production Engineering and Management 14
Coordinates
X1 X2
Constraint 1 80 0
Constraint 2 0 60
Constraint 3
0 100
120 0
Constraint 4
0 80
160 0
Step 3.Make a table listing the value of the objective function at each corner point.
In the above figure, there is no unique outer most corner cut by the objective function line. All
points from B to C lying on line BC represent optimal solutions and all these will give the same
optimal value (maximum profit) of 160. This is indicated by the fact that both the points B with
co-ordinates (40, 60) and C with co-ordinates (60, 50) are on the line X1 + 2X2 = 160.Thus,
every point on the line BC maximizes the value of the objective function and the problem has
multiple solutions.
Corner points Maximize Z = X1 + 2X2
A (0,60) 120
B (40,60) 160
C (60,50) 160
D(80,100/3) 0
E (80,0) 0
Step 4.Determine the optimal solution from the table in step 3;
Then from step three the problem is Maximization problem then the Maximum
point is at point B and C (Optimal point) with the values of X1 and X2 are40 and
60 at point B respectively or 60 and 50 at point C respectively in which the

15. Compiled by Tsegay Berhe MSc in Production Engineering and Management 15
objective value equals to 160 at both corner points. X1=40, X2=60, Z=160 or
X1=60, X2=50, Z=160
b) Unbounded Solution; It is a solution whose objective function is infinite. If the feasible
region is unbounded then one or more decision variables will increase indefinitely
without violating feasibility, and the value of the objective function can be made
arbitrarily large. Consider the following model:
Example
Minimize Z = 40X1 + 60X2
subject to
2X1+ X2 ≥ 70
X1 + X2 ≥ 40
X1 + 3X2 ≥ 90
X1, X2 ≥ 0
Solution
The point (X1, X2) must be somewhere in the solution space as shown in the figure by
shaded portion. The three extreme points (corner points) in the finite plane are: C = (90,
0); B = (24, 22) and A = (0, 70) The values of the objective function at these extreme
points are: Z(c) = 3600, Z(B) = 2280 and Z(A) = 4200.
In this case, no maximum of the objective function exists because the region has no
boundary for increasing values of X1 and X2. Thus, it is not possible to maximize the
objective function in this case and the solution is unbounded.
c) Infeasible Problem
In some cases, there is no feasible solution area, i.e., there are no points that satisfy all
constraints of the problem. An infeasible LP problem with two decision variables can be
identified through its graph. For example, let us consider the following linear
programming problem.
Minimize Z = 200X1 + 300X2
subject to
2X1 + 3X2 ≥ 1200
X1 + X2 ≤ 400

16. Compiled by Tsegay Berhe MSc in Production Engineering and Management 16
2X1 + 1.5X2 ≥ 900
X1, X2 ≥ 0
The region located on the right of ABC includes all solutions, which satisfy the first and
the third constraints. The region located on the left of DE includes all solutions, which
satisfy the second constraint. Thus, the problem is infeasible because there is no set of
points that satisfy all the three constraints.
GRAPHICAL SENSITIVITY ANALYSIS
In LP, the input data (parameters) of the model can change within certain limits without causing
the optimum solution to change. Two cases will be considered.
 Sensitivity of the optimum solution to changes in the availability of the resources
(changes in the right-hand side value of constraints).
 Sensitivity of the optimum solution to changes in unit profit or unit cost (Change in the
coefficients of the objective function).
Sensitivity analysis (or post-optimality analysis) is used to determine how the optimal solution is
affected by changes, within specified ranges, in:
a. the objective function coefficients
b. the right-hand side (RHS) values
Sensitivity analysis is important to the manager who must operate in a dynamic environment
with imprecise estimates of the coefficients. Sensitivity analysis allows him to ask certain what-if
questions about the problem.
EXAMPLE

17. Compiled by Tsegay Berhe MSc in Production Engineering and Management 17
Max Z = 30X1 + 20X2
subject to
2X1 + X2 ≤ 8
X1 + 3X2 ≤ 8
X1, X2 ≥ 0
Solution
Then from the above figure the optimal points are at corner point B with X1=16/5 and X2 =8/5
and the objective function value is Z=128.
a. Change in the Objective Function Coefficients
Let us consider how changes in the objective function coefficients might affect the
optimal solution. The range of optimality for each coefficient provides the range of
values over which the current solution will remain optimal. Managers should focus on
those objective coefficients that have a narrow range of optimality and coefficients near
the endpoints of the range.
The range of optimality is determined based on the binding constraints. Binding
constraint is in which the right-hand side is equal to the left-hand side of the constraints.
Checking which constraint is a binding constraint.
2X1 + X2 = 8, (2*16/5+8/5) =8
X1 + 3X2 = 8, (16/5+3*8/5) =8
Then both constraint 1 and 2 are binding constraints.
Range of Optimality; Graphically, the limits of a range of optimality are found by
changing the slope of the objective function line within the limits of the slopes of the
binding
constraint lines.
The slope of an objective function line, Max C1X1 + C2X2, is -C1/C2, and the slope of a
constraint, a1X1 + a2X2 = b, is -a1/a2.
1. Range of Optimality for C1

18. Compiled by Tsegay Berhe MSc in Production Engineering and Management 18
The slope of the objective function line is -C1/C2. The slope of the first binding constraint,
2X1 + X2 = 8, is -2 and the slope of the second binding constraint, X1 + 3X2= 8, is -1/3.
Find the range of values for C1 (with C2 staying 20) such that the objective function line
slope lies between that of the two binding constraints:
-2 ≤-C1/20 ≤-1/3
-40 ≤ - C1≤-20/3 [Multiplying through by -20 and reversing the inequalities):
20/3≤ C1≤40
2. Range of Optimality for C2
Find the range of values for C2 (with C1 staying 30) such that the objective function line
slope lies between that of the two binding constraints:
-2 ≤-30/ C2≤-1/3 [Multiplying through by -1 and reversing the inequalities):
2 ≥30/C2 ≥1/3
1/2≤ C2/30≤3
15≤ C2 ≤ 90
b. Right-Hand Sides
Let us consider how a change in the right-hand side for a constraint might affect the feasible
region and perhaps cause a change in the optimal solution. The improvement in the value of the
optimal solution per unit increase in the right-hand side is called the dual price. The range of
feasibility is the range over which the dual price is applicable. As the RHS increases, other
constraints will become binding and limit the change in the value of the objective function.
Graphically, a dual price is determined by adding +1 to the right-hand side value in question
and then resolving for the optimal solution in terms of the same two binding constraints. The
dual price is equal to the difference in the values of the objective functions between the new and
original problems.
The dual price for a nonbinding constraint is zero. A negative dual price indicates that the
objective function will not improve if the RHS is increased.
A resource cost is a relevant cost if the amount paid for it is dependent upon the amount of the
resource used by the decision variables. Relevant costs are reflected in the objective function
coefficients. A resource cost is a sunk cost if it must be paid regardless of the amount of the
resource actually used by the decision variables. Sunk resource costs are not reflected in the
objective function coefficients.
Resource cost is sunk; if the dual price is the maximum amount you should be willing to pay for
one additional unit of the resource.
Resource cost is relevant; if the dual price is the maximum premium over the normal cost that
you should be willing to pay for one unit of the resource.
Dual Prices: since both constraints are binding, they have a dual price.
Constraint 1: Change the RHS value of the first constraint to 9 and resolve for the optimal point
determined by the last two constraints:
Max Z = 30X1 + 20X2
subject to
2X1 + X2 ≤ 9

19. Compiled by Tsegay Berhe MSc in Production Engineering and Management 19
X1 + 3X2 ≤ 8
X1, X2 ≥ 0
Solution
The solution is X1 = 19/5, X2 = 7/5, z = 142. Hence, the dual price = Znew - Zold = 142 - 128 = 14
Constraint 2: Change the RHS value of the third constraint to 9 and resolve for the optimal point
determined by the last two constraints:
Max Z = 30X1 + 20X2
subject to
2X1 + X2 ≤ 8
X1 + 3X2 ≤ 9
X1, X2 ≥ 0
Solution
The solution is X1 = 3, X2 = 2, z = 130. Hence, the dual price = Znew - Zold = 130 - 128 = 2

20. Compiled by Tsegay Berhe MSc in Production Engineering and Management 20
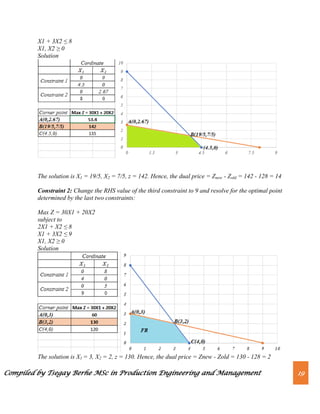
The dual price is also equal to the shadow price.
[ ]
[ ]
[ ]
Range of Feasibility; The range of feasibility for a change in the right-hand side value is the
range of values for this coefficient in which the original dual price remains constant.
Graphically, the range of feasibility is determined by finding the values of a right-hand side
coefficient such that the same two lines that determined the original optimal solution continue to
determine the optimal solution for the problem.