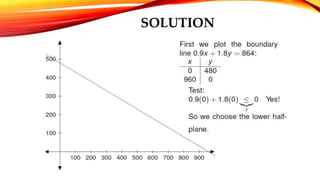
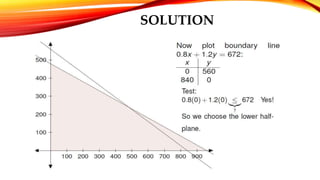
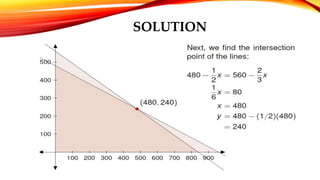
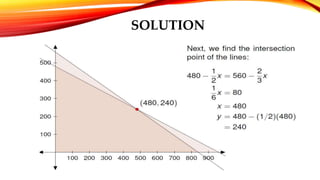
The document provides an introduction to linear programming, which is a mathematical method used for optimal resource allocation among competing activities, focusing on maximizing profits or minimizing costs. It outlines key concepts, applications, advantages, limitations, and methods for solving linear programming problems, emphasizing the importance of constraints and decision variables. Additionally, an example is given that demonstrates the application of these principles in maximizing profit for a manufacturing scenario.

1. INTRODUCTION TO
LINEAR
PROGRAMING
Dr. Muhammad Junaid

2. LINEAR PROGRAMMING
⮚ What is Linear Programming?
• The word linear means the relationship which can be represented by a
straight line .i.e the relation is of the form
ax +by=c
• In other words it is used to describe the relationship between two or more
variables which are proportional to each other
• The word “programming” is concerned with the optimal allocation of
limited resources
• Linear programming is a way to handle certain types of optimization
problems
• Linear programming is a mathematical method for determining a way to
achieve the best outcome

3. DEFINITION OF LINEAR
PROGRAMMING
⮚LP is a mathematical modeling technique useful for the allocation of “scarce
or limited’’ resources such as:
• Labor
• Material
• Machine
• Time
• warehouse space ,etc..
⮚ To several competing activities such as:
• Product
• Service
• Job
• New equipment’s
• Projects, etc..
⮚On the basis of a given criteria of optimality

4. LINEAR PROGRAMMING
⮚ A mathematical technique used to obtain an optimum solution in resource
allocation problems, such as production planning.
⮚ It is a mathematical model or technique for efficient and effective utilization
of limited recourses to achieve organization objectives (Maximize profits or
Minimize cost)
⮚ When solving a problem using linear programming, the program is put into
a number of linear inequalities and then an attempt is made to maximize (or
minimize) the inputs

5. REQUIREMENTS
⮚ There must be well defined objective function
⮚ There must be a constraint on the amount
⮚ There must be alternative course of action
⮚ The decision variables should be interrelated and non negative
⮚ The resource must be limited in supply

6. ASSUMPTIONS
⮚ Proportionality
⮚ Additivity
⮚ Continuity
⮚ Certainty
⮚ Finite Choices

7. APPLICATION OF LINEAR
PROGRAMMING
⮚ Business
⮚ Industrial
⮚ Military
⮚ Economic
⮚ Marketing
⮚ Distribution

8. AREAS OF IMPLEMENTATION
OF LINEAR PROGRAMMING IN
PROBLEM SOLVING
⮚ Industrial Application
• Product Mix Problem
• Blending Problems
• Production Scheduling Problem
• Assembly Line Balancing
• Make-Or-Buy Problems
⮚ Management Applications
• Media Selection Problems
• Portfolio Selection Problems
• Profit Planning Problems
• Transportation Problems

9. AREAS OF IMPLEMENTATION OF
LINEAR PROGRAMMING IN
PROBLEM SOLVING
⮚ Miscellaneous Applications
• Diet Problems
• Agriculture Problems
• Flight Scheduling Problems
• Facilities Location Problems

10. ADVANTAGES OF LINEAR
PROGRAMMING
⮚ It helps in attaining optimum use of productive factors
⮚ It improves the quality of the decisions
⮚ It provides better tools for meeting the changing conditions
⮚ It highlights the bottleneck in the production process

11. LIMITATIONS OF LINEAR
PROGRAMMING
⮚ For large problems the computational difficulties are
enormous
⮚ It may yield fractional value answers to decision variables
⮚ It is applicable to only static situation
⮚ LP deals with the problems with single objective

12. TYPES OF SOLUTIONS IN LINEAR
PROGRAMMING
The solution of an LP problem, (also known as FEASIBLE SOLUTION) is
actually the optimum level of the decision variables where all the constraints
are satisfied. There are two methods for reaching an optimal feasible
solution:
⮚ Graphical Method
• Corner Point Solution Method
• Isopointl Line Solution Methods
⮚ Simplex Method
• Maximization for Constraint
• Minimization or Maximization for Constraints

13. FORMS OF LINEAR PROGRAMMING
⮚ The canonical form
• Objective function is of maximum type
• All decision variables are non negative
⮚ The Standard Form
• All variables are non negative
• The right hand side of each constraint is non negative
• All constraints are expressed in equations
• Objective function may be of maximization or
minimization type

14. IMPORTANT DEFINITIONS
IN LINEAR PROGRAMMING
⮚ Solution:
• A set of variables [X1,X2,...,Xn+m] is called a solution to L.P.
Problem if it satisfies its constraints
⮚ Feasible Solution:
• A set of variables [X1,X2,...,Xn+m] is called a feasible solution to L.P.
Problem if it satisfies its constraints as well as non-negativity
restrictions
⮚ Optimal Feasible Solution:
• The basic feasible solution that optimizes the objective function
⮚ Unbounded Solution:
• If the value of the objective function can be increased or decreased
indefinitely, the solution is called an unbounded solution

15. VARIABLES USED IN LINEAR
PROGRAMMING
⮚ Slack Variable
• Non-negative variables, added to the L.H.S of the constraints to change
the inequalities to equalities. Added when the inequalities are of the
type (<=).
⮚ Surplus Variable
• In some L.P problems slack variables cannot provide a solution. These
problems are of the types (>=) or (=) . Artificial variables are introduced
in these problems to provide a solution.
⮚ Artificial Variable
• Artificial variables are introduced in these problems to provide a
solution.

16. EXAMPLE
⮚ A manufacturing plant makes two types of inflatable boats, a two-person
boat and a four-person boat. Each two-person boat requires 0.9 labor hours
from the cutting department and 0.8 labor-hours from the assembly
department. Each four person boat requires 1.8 labor-hours from the
cutting department and 1.2 labor-hours from the assembly department. The
maximum labor hours available per month in the cutting department and
the assembly department are 864 and 672, respectively. The company
makes a profit of 25 on each 2-person boat and 40 on each 4-person boat.
1. How many of each type should be manufactured each month to
maximize profit?
2. What is the maximum profit?

17. SOLUTION
⮚ To solve such a problem involves:
1. Constructing a mathematical model of the problem
2. Using the mathematical model to find the solution
⮚ Step 1: Identify the decision variables
In this problem, we have:
• x = number of 2-person boats to manufacture
• y = number of 4-person boats to manufacture
⮚ Step 2: Summarize relevant information in table form, relating the decision
variables with the rows in the table, if possible

18. SOLUTION
⮚ Recall the data provided in the question
• Each two-person boat requires 0.9 labor hours from the cutting department
and 0.8 labor-hours from the assembly department. Each four person boat
requires 1.8 labor-hours from the cutting department and 1.2 labor-hours from
the assembly department
• The maximum labor-hours available per month in the cutting department and
the assembly department are 864 and 672, respectively. The company makes a
profit of 25 on each 2person boat and 40 on each four-person boat.

19. SOLUTION
⮚ Step 3: Determine the objective and write a linear objective function
P = 25x + 40y
⮚Step 4: Write problem constraints using linear equations and/or inequalities
0:9x + 1:8y ≤ 864
0:8x + 1:2y ≤ 672
⮚Step 5: Write nonnegative constraints.
x > 0
y > 0
⮚ We now have a mathematical model of the given problem. We need to find
the production schedule which results in maximum profit for the company
and to find that maximum profit.

20. SOLUTION
⮚ Now we follow the procedure for geometrically solving a linear
programming problem with two decision variables
⮚Applying the Fundamental Theorem of Linear Programming
• Graph the feasible region. Be sure to find all corner points
• Construct a corner point table listing the value of the objective
function at each corner point
• Determine the optimal solution(s) from the table
• For an applied problem, interpret the optimal solution(s) in
terms of the original problem.

21. SOLUTION
⮚ Now we follow the procedure for geometrically solving a linear
programming problem with two decision variables
⮚Applying the Fundamental Theorem of Linear Programming
• Graph the feasible region. Be sure to find all corner points
• Construct a corner point table listing the value of the objective
function at each corner point
• Determine the optimal solution(s) from the table
• For an applied problem, interpret the optimal solution(s) in
terms of the original problem.

22. SOLUTION

23. SOLUTION

24. SOLUTION

25. SOLUTION

26. SOLUTION

27. SOLUTION
⮚ Now we solve the problem:
• Corner Point: P = 25x + 40y
• (0; 0) 0
• (0; 480) 19,200
• (480; 240) 21,600
• (840; 0) 21,500
⮚Hence, we conclude that the company can make a maximum profit of
21,600 by producing 480 two-person boats and 240 four-person boats