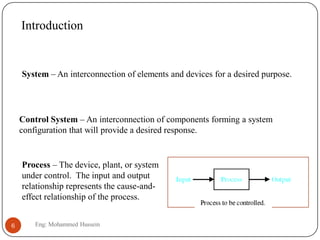
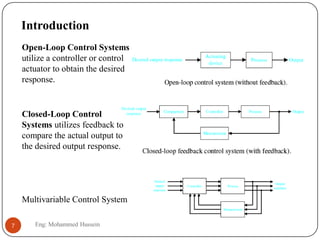
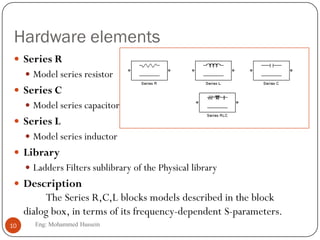
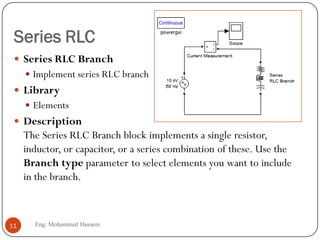
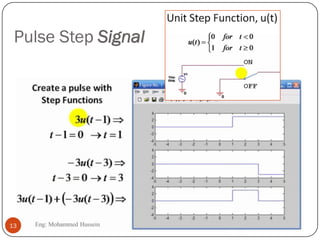
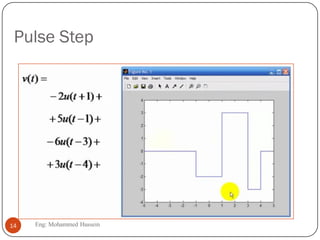
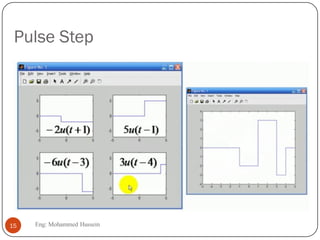
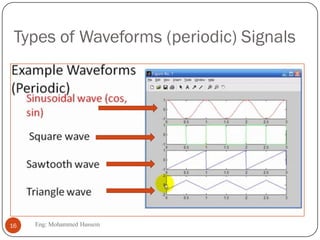
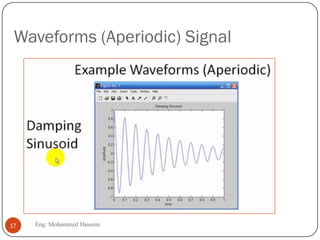
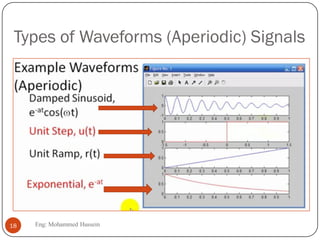
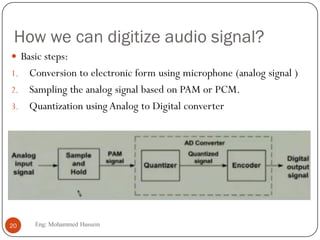
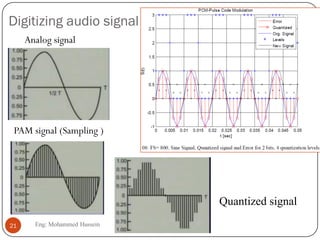
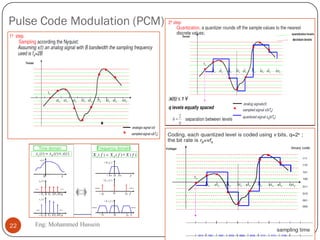
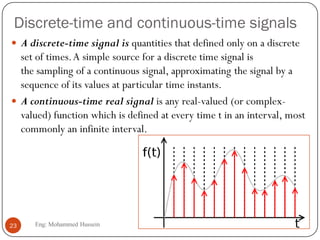
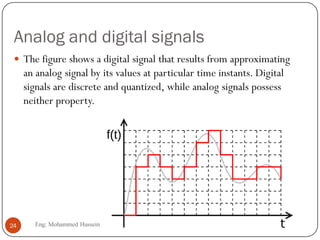
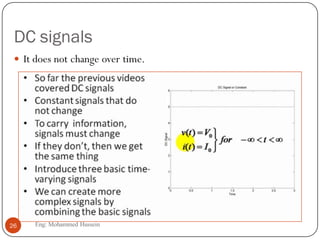
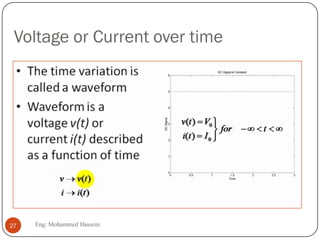
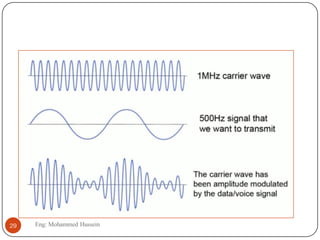
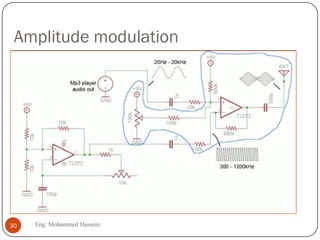
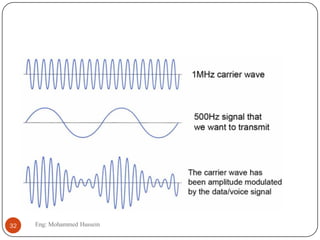
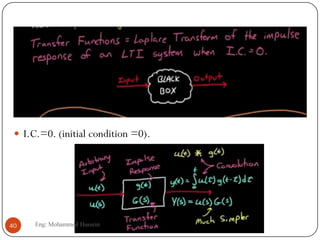
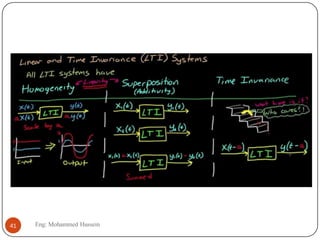
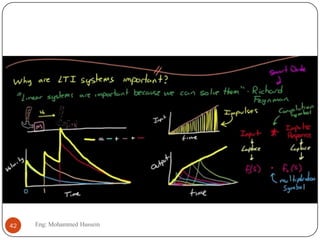
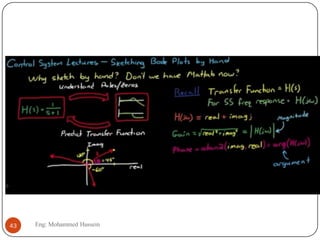
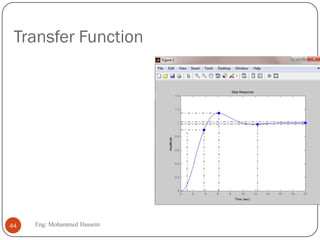
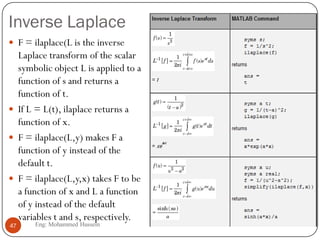
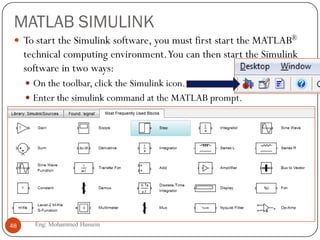
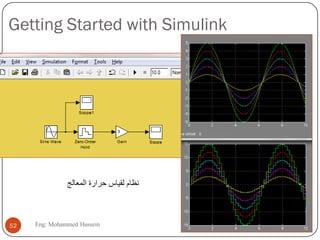
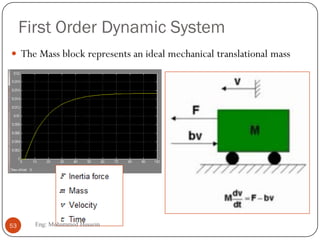
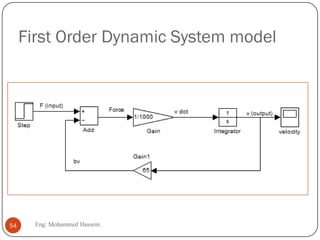
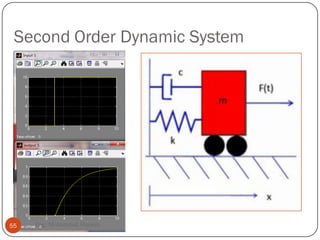
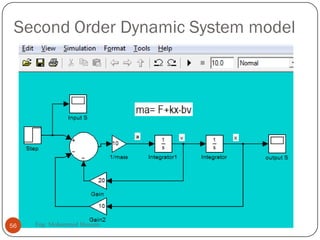
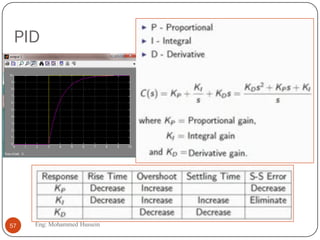
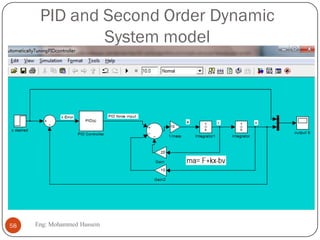
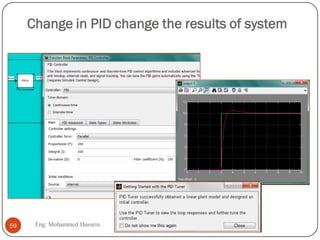
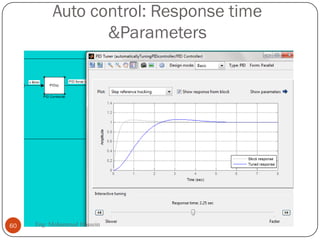
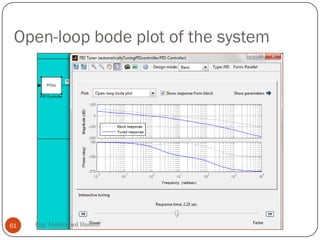
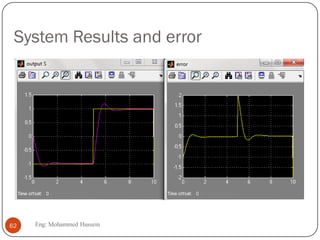
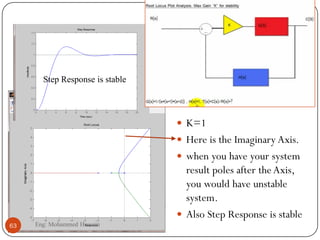
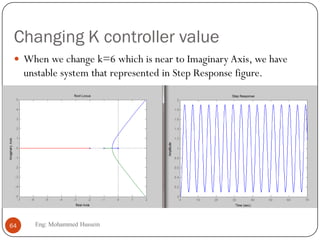
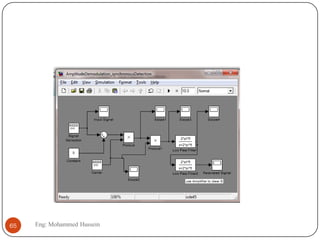
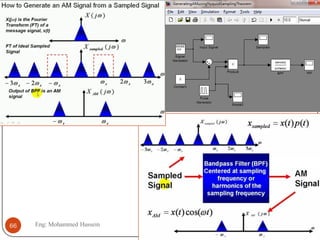
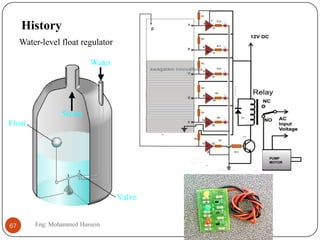
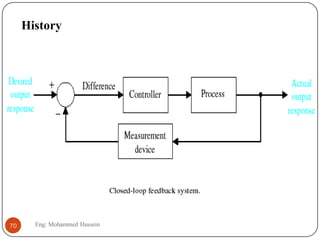
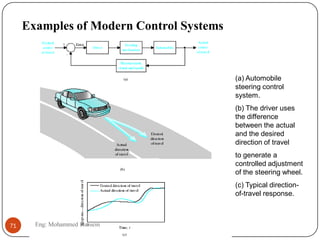
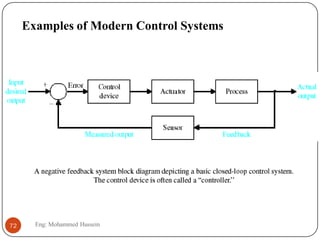
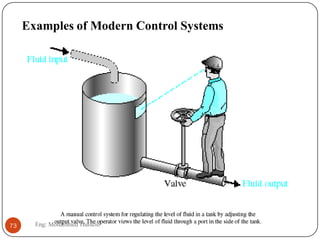
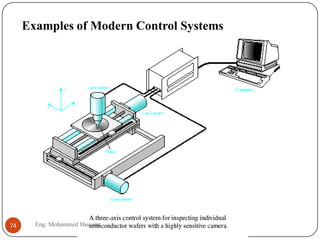
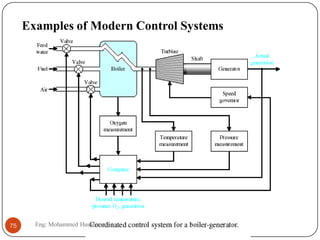
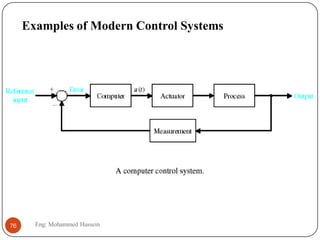
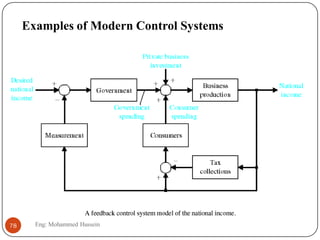
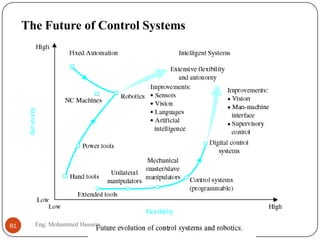
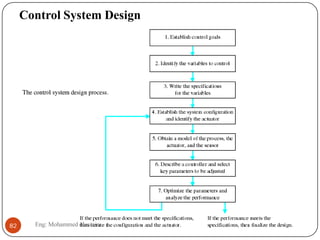
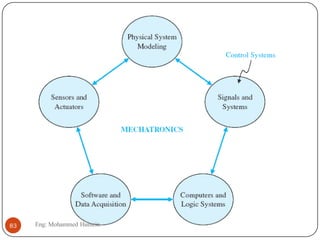
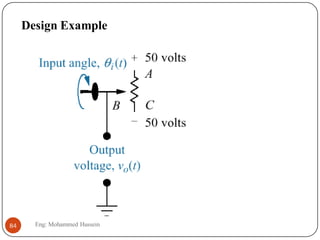
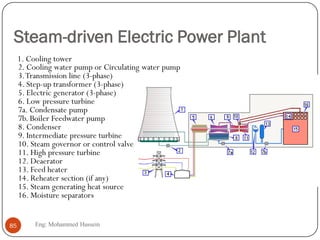
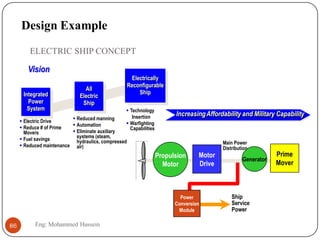
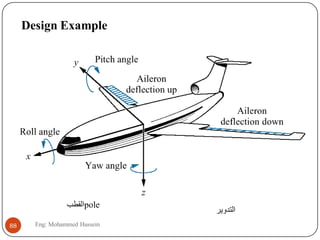
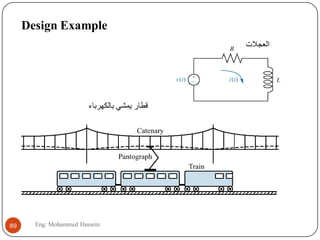
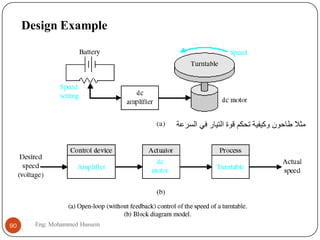
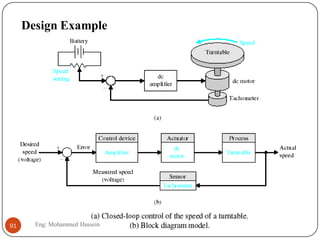
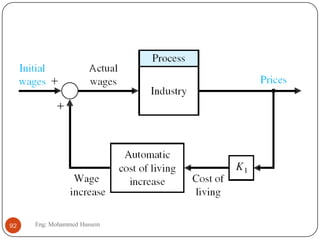
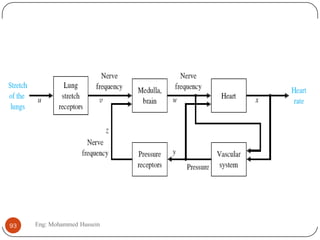
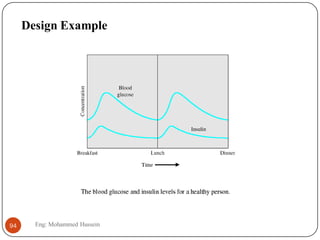
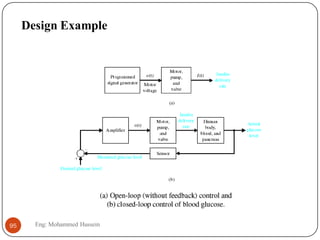
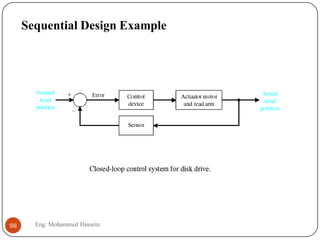
The document provides an overview of control systems and related concepts. It discusses the history of control systems from the 18th century to present day. Key concepts covered include open-loop and closed-loop control systems, transfer functions, Laplace transforms, and modeling systems in MATLAB Simulink. The document is intended to introduce students to control systems by describing the objectives and components of a general control system design process.