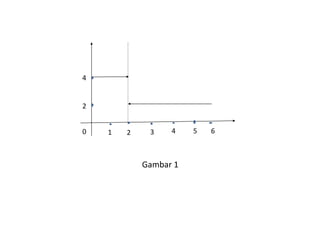
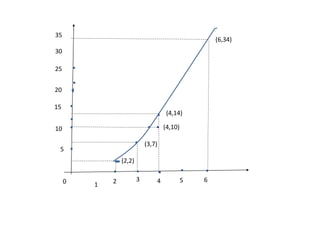
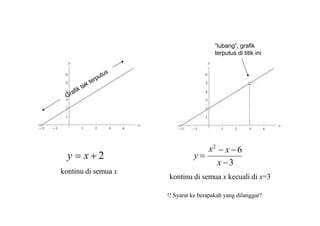
Dokumen ini membahas konsep limit dan kontinuitas dalam fungsi matematika, termasuk limit kiri dan kanan serta syarat-syarat agar fungsi dapat dinyatakan kontinu. Fungsi dikatakan kontinu jika memenuhi tiga syarat: nilai fungsi terdefinisi, limit eksis, dan limit sama dengan nilai fungsi pada titik tersebut. Terdapat juga contoh-contoh fungsi kontinu dan diskontinu yang menjelaskan aplikasi praktis dari konsep ini.

1. Limit dan kontinuitas fungsi

2. Limit fungsi
• Diberikan fungsi f(x) dengan domain bilangan riil
• Jika nilai fungsi f(x) semakin mendekati sebuah
bilangan L jika x semakin mendekati a (namun x tidak
sama dengan a), maka dikatakan “L adalah limit dari
f(x) ketika x mendekati a”.
• Dinotasikan sebagai:
lim f (x)  L
xa

3. • Teknik mencari limit suatu fungsi tidak
dibahas dalam materi ini.
• Materi ini memperkenalkan konsep limit
lanjutan: limit kiri, limit kanan, dan kontinuitas
fungsi

4. Limit kiri dan limit kanan
lim f (x)
xa
Limit kiri [kanan] adalah limit dari sebuah fungsi f(x)
untuk x mendekati a dari arah kiri [kanan].
lim f (x)
xa
limit dari f(x) untuk x mendekati a dari
arah kiri
limit dari f(x) untuk x mendekati a dari
arah kanan
xa
xa
xa
lim f (x) ada jika dan hanya jika lim f (x)  lim f (x)

5.  
 
1
lim
x10
10  x
1
lim
x10
10  x
lim x  3  5 (ada)
x2
x 2
Apakah lim x  3 ada?
lim x  3  5
lim x  3  5
x2
x2
limit kiri = limit kanan
tidak ada limit
Contoh 1
Contoh 2 ?
1
Bagaimana dengan lim
x10 10  x

6. lim f (x)  ?
f (x) 
x 1, jika x  5
x5

x  2, jika x  5
lim f (x)  5 2  7
lim f (x)  51 6
x5
x5
maka lim f (x) tidak ada
x5
lim f (x)  lim f (x),
x5
x5
Contoh 3 Kalau yang berikut ini bagaimana?

7. lim f (x)  ?
f (x) 
x 1, jika x  7
x7

2x-6, jika x  7
lim f (x)  2(7)  6  8
lim f (x)  7 1 8
x7
x7 lim f (x)  lim f (x)  8
x7
x7
limitnya ada!!
Contoh 4 Kalau yang ini?

8. n
a  a x  a x2
… a x
0 1 2 n
Pada fungsi polinomial
limit kiri = limit kanan di semua x

9. KONTINUITAS
Pembahasan tentang konsep limit pada bagian terdahulu
digunakan untuk menentukan apakah suatu fungsi kontinu
atau diskontinu. Hal ini dikarenakan bahwa antar konsep
limit dengan kontinuitas mempunyai hubungan yang erat.
Dipandang dari segi grafik, bila suatu fungsi dapat
digambarkan diatas kertas tanpa mengangkat pena atau
pensil dari kertas tersebut, maka fungsi itu dinamakan
kontinu (berkesinambungan). Sedangkan jika
menggambarnya terdapat garis putus-putus atau garis
patah, fungsi tersebut dinamakan diskontinu.

10. Untuk suatu fungsi f(X) menjadi kontinu pada titik X =
N, ada tiga syarat yang harus dipenuhi, yaitu :
(1). f(N) harus terdefinisi
(2). lim
𝑥→𝑁
𝑓 𝑁 harus ada
(3). lim
𝑥→𝑁
𝑓 𝑁 f(X) = g(N)
Jadi untuk suatu fungsi akan menjadi kontinu pada suatu
titik haruslah memenuhi ketiga persyaratan diatas yaitu :
(1). Titik N harus berada dalam domain fungsi;
(2). Fungsi harus mempunyai limit pada titik tersebut:
(3). Limit pada titik tersebut harus sama dengan nilai
f(N) pada titik tersebut

11. Perlu diingat, bahwa jika salah satu dari ketiga
persyaratan tersebut tidak dipenuhi, fungsi f(X) tidak
kontinu pada X = N. Dengan kata lain, fungsi f(X)
tidak kontinu (diskontinu).
Berikut beberapa contoh kontinu dan discontinue dari
suatu fungsi.

12. Kontinuitas fungsi
3.lim f (x)  f (a)
xa
xa
Fungsi f(x) dikatakan kontinu
(berkesinambungan) pada x = a jika dan hanya
jika ketiga syarat berikut terpenuhi:
1. f (a) terdefinisi
2.lim f (x) ada
Jika minimal satu syarat tidak terpenuhi,
maka f (x) tidak kontinu (diskontinu) di x  a

13. Contoh :
Jika f(X) =
(𝑋2 −4)
(𝑋 −2)
, maka lim
𝑥→2
𝑋2 −4
𝑋 −2
=
(𝑋+2)(𝑋 −2)
𝑋 −2
= 2+2=4 (ada)
dan f(2) =
(22 −4)
(2 −2 )
= 0 (tidak terdefinisi)
Jadi walaupun lim
𝑥→2
𝑋2 −4
𝑋 −2
ada, fungsi tidak kontinu pada x = 2
Contoh :
Misalkan fungsi tangga
4 untuk 0 < X < 3
f(X) = 2 untuk X > 3
Fungsi ini dapat dilihat pada Gambar berikut. Pada titik X = 3 fungsi
terdefinisi, karena f(3) = 2, tetapi limit X mendekati 3 tidak ada. Oleh karena
itu, terdapat diskontinu pada titik ini.

14. 0 1 2 3 4 5 6
2
4
Gambar 1

15. Contoh :
Misalkan fungsi tangga
- 2 untuk semua X kecuali 4
f(X) = 10 untuk X = 4
Penyelidikan ketika X mendekati 4 ada, karena
lim
𝑥→4
𝑋2 - 2 = 42 - 2 = 14
dan f(X) terdefinisis pada X = 4 karena f(X) = 10 pada titik ini. Akan tetapi
lim
𝑥→4
𝑋2
- 2 ≠ f(4)
Dengan demikian terdapat diskontinu pada fungsi di titik X = 4
(Lihat gambar berikut)
𝑋2

16. (2,2)
(3,7)
(4,14)
1
5
3 4 5 6
0 1
10
15
2
20
25
30
35
(4,10)
(6,34)

17. Apakah f (x)  x  3 kontinu di x  2?
3.lim f (x)  f (2)  5
1. f (2)  2  3  5 ( f (2) terdefinisi)
2.lim f (x)  5 (limitnya ada)
x2
x2
Ketiga syarat terpenuhi. Jawaban atas pertanyaan di
atas adalah: Ya
Contoh 5

18. 
Apakah f (x) kontinu di x  5?
x  2, jika x  5
Diberikan f (x) 
x 1, jika x  5
f (x) melanggar syarat kedua (lihat kembali Contoh 3)
Jawabannya adalah: Tidak.
Contoh 6
Catatan: Karena syarat ke dua dilanggar, maka pemeriksaan syarat ketiga
adalah opsional (boleh/tidak dilakukan)

22. n
a  a x  a x2
… a x
0 1 2 n
adalah kontinu semua x
Fungsi polinomial

23. Secara grafis,
• fungsi yang kontinu di semua titik domainnya
memiliki grafik yang tidak terputus
• fungsi yang diskontinu pada satu/beberapa titik
ataupun pada interval tertentu memiliki lubang,
celah, maupun "lompatan" pada grafiknya

24. y  x  2
kontinu di semua x
x 3
 x 6
x2
y 
kontinu di semua x kecuali di x=3
“lubang”, grafik
terputus di titik ini
!! Syarat ke berapakah yang dilanggar?

25.  1, jika x  0
f (x) 
-1, jika x  0

Kontinu di semua x kecuali di x = 0.
(Terdapat "lompatan" fungsi pada
x = 0)
!! Syarat ke berapakah yang dilanggar?
0 X
Y

26. Konsep tambahan:
• Sifat-sifat limit
• Diskontinu yang dapat dihapus (removable
discontinuity)
• Kontinu kiri [kanan]
Silakan pelajari dalam:
Ayres dan Medelson, “Calculus”, Schaum Series, McGraw Hill

27. DEFINISI DEFINISI KONTINUITAS
1. Suatu fungs f(X) dikatakan menjadi kontinu dalam
suatu interval terbuka jika fungsi tersebut adalah
kontinu pada setiap titik dalam interval itu.
2. Jika f(X) = K dimana K adalah suatu konstanta,
maka f(X) adalah kontinu pada semua X.
3. Jika f(X) = 𝑋𝑛
dimana n adalah bilangan bulat
positif, maka f(X) adalah kontinu pada semua X.
4. Jika f(X) adalah kontinu pada 𝑋0 dalam domainnya
dan K adalah konstanta, maka f(X) adalah kontinu
pada 𝑋0.

28. DEFINISI DEFINISI KONTINUITAS
5. Jika f(X) dan g(X) adalah kontinu padatitik 𝑋0 dimana 𝑋0
adalah dalam domain dari kedua fungsi f dan g, maka F(X),
G(X) dan H(X) ditentukan oleh,
F(X) = f(X) + g(X)
G(X) = f(X) – g(X)
H(X) = f(X).g(X) adalah kontinu pada 𝑋0.

29. DEFINISI DEFINISI KONTINUITAS
Dalam penerapan bidang ekonomi dan bisnis fungsi
diskontinu kebanyakan ditemukan, misalnya : fungsi
permintaan komputear, dimana jumlah yang diminta
akan produk ini tidak bisa suatu angka pecahan,
misalnya 45,4 unit computer. Akan tetapi demi
memudahkan analisis, para anlisis atau ekonom
mengasumsikan bahwa fungsi-fungsi yang diskontinu
dianggap menjadi kontinu, Jadi kebanyakan fungsi-
fungsi yang digunakan dalam ekonomi dan bisnis
adalah fungsi kontinu.