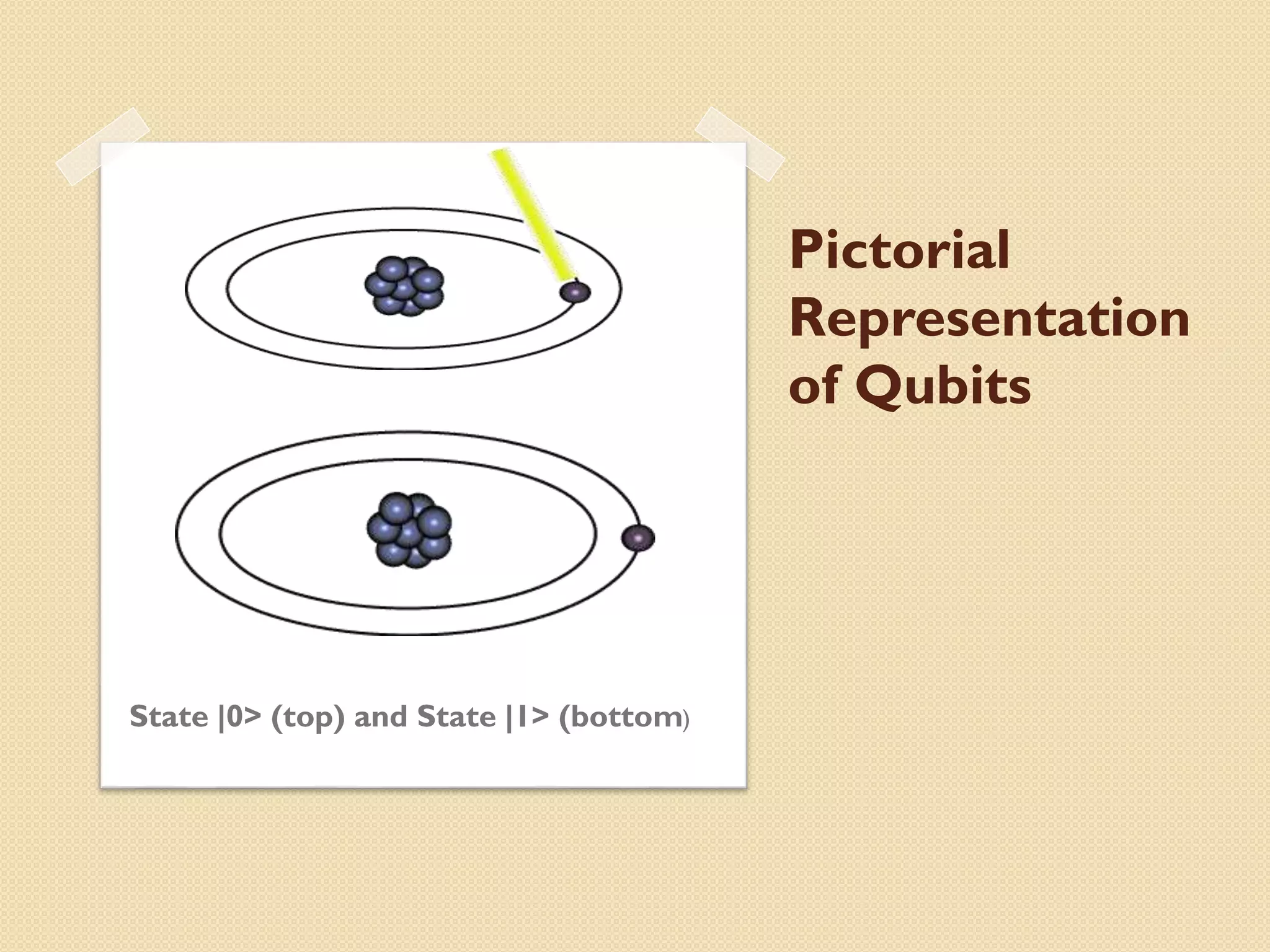
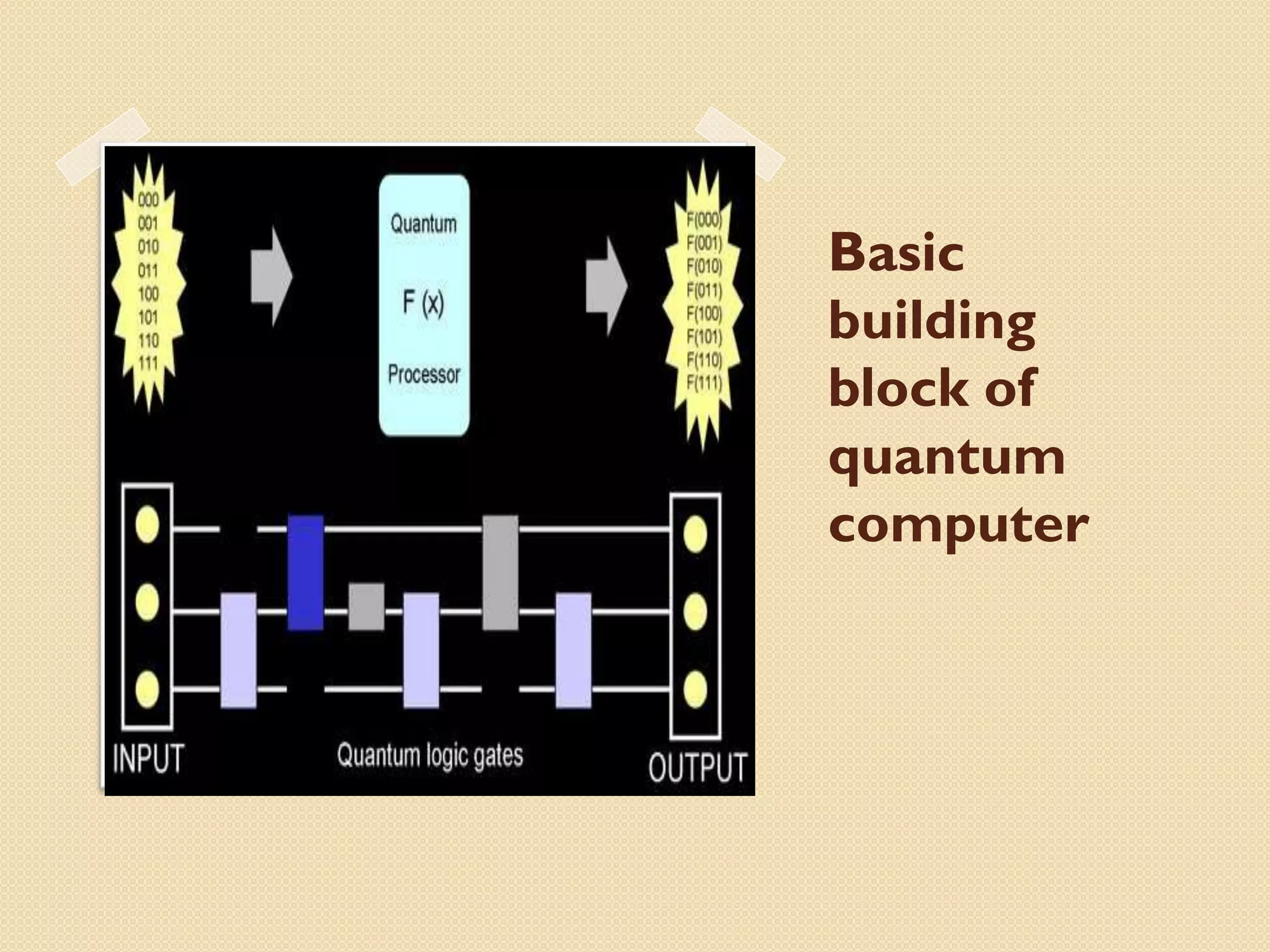
This document discusses quantum computers, which harness quantum phenomena like superposition and entanglement to perform operations. A qubit, the basic unit of information in a quantum computer, can exist in multiple states simultaneously. While this allows massive parallelism and an exponential increase in computational power over classical computers, building large-scale quantum computers faces challenges in maintaining coherence. Potential applications include cryptography, optimization problems, and software testing due to quantum computers' probabilistic solving approach.

1. Quantum Computer
By Ritikesh Bhaskarwar
Department of ComputerTechnology
YESHWANTRAO CHAVAN COLLEGE OF ENGINEERING, Nagpur
(An Autonomous Institution Affiliated to
RashtrasantTukadoji Maharaj Nagpur University)

2. Introduction :
 A quantum computer is a device
for computation that makes direct use
of quantum mechanical phenomena, such
as superposition and entanglement, to
perform operations on data.
 It harnesses the power of atoms and
molecules to perform memory and
processing tasks.

3.  If, as Moore's Law states, the number of
transistors on a microprocessor continues
to double every 18 months, the year 2020
or 2030 will find the circuits on a
microprocessor measured on an atomic
scale.
 The logical next step will be to create
quantum computers, which will harness the
power of atoms and molecules to perform
memory and processing tasks.

4. History :
 Richard Feynman observed in the early
1980s [Feynman 1982] that certain
quantum mechanical effects cannot be
simulated efficiently on a classical
computer.
 It wasn’t until 1994, when Peter Shor
surprised the world by describing a
polynomial time quantum algorithm for
factoring integers [Shor 1994; 1997]

5. Literature Survey:
 E.Rieffel,W.Polak,”An IntroductionTo
Quantum Computing for Non-Physicist”,
ACM Computing Survey,Vol. 32, No.3
(2000).
=> It introduces basic principles of
quantum mechanics to explain where the
power of quantum computers comes
from and why it is difficult to harness.

6.  D.DiVincenzo, ”Quantum Computation”, Science,
New Series,Vol. 270, No.5234 (2006).
=> It is evident from this survey of the
current state of art in quantum experimental
physics that construction of quantum computer
is presently in most rudimentary stage.
 C.H.Bennet, ”Quantum Information And
Computation”, Physics Today, American Institute
of Physics (1995).
=> The quantum information processing
involves quantum states which is described by a
wave function or a state in a Hilbert space

7. Background Knowledge :
 Superposition
Definition :- Two things can overlap each
other without interfering with each other.
In classical computers, electrons cannot
occupy the same space at the same time,
but as waves, they can.
 A single qubit can be forced into a
superposition of the two states denoted
by the addition of the state vectors:

8. A qubit in
superposition
is in both of
the states |1>
and |0> at the
same time
Superposition

9.  Entanglement
 Entanglement is the ability of quantum
systems to exhibit correlations between
states within a superposition.
 Imagine two qubits, each in the state |0>
+ |1> (a superposition of the 0 and 1.)
We can entangle the two qubits such that
the measurement of one qubit is always
correlated to the measurement of the
other qubit.

10. Quantum Bits:
 A quantum bit, or qubit, is a unit vector
in a two-dimensional complex vector
space for which a particular basis,
denoted by {|0>,|1>}, has been fixed.
 The orthonormal basis |0> and |1> may
correspond to the |↑> and |→>
polarizations of a photon respectively

11. Pictorial
Representation
of Qubits
State |0> (top) and State |1> (bottom)

12. Bits v/s Qubits
Bits Qubits
 The device computes by
manipulating those bits
with the help of logic gates
 A classical computer has a
memory made up of bits ,
where each bit holds either
a one or a zero
 A qubit can hold a one, a
zero, or, crucially, a
superposition of these
,manipulating those qubits
with the help of quantum
logic gates
 The qubits can be in a
superposition of all the
classically allowed states.

13. Basic
building
block of
quantum
computer

14. Quantum Dots :
 A quantum dot is a semiconductor
nanostructure that confines the motion of
conduction band electrons
valence band holes
or excitons (pairs of conduction band
electrons and valence band holes)
,in all three spatial directions.

15. UNIVERSAL QUANTUM LOGIC
GATE
 It is realized with high-finesse microwave
cavities and two-state atoms.
 All possible quantum computations can
be built up with a network of such gates.
 More general output states can be
obtained by adjusting the atom-cavity
interactions and adding another Ramsey
zone

16. Quantum Logic Gate :

17. Advantages :
 Exponential computing power, combined
with the fact that a qubit can be
simultaneously a one and zero at the
same time, gives quantum computers
another edge over binary.
 It can explore different solutions
simultaneously, instead of one at a time.
Imagine having thousands of computers
working in unison to solve your problem.

18.  They can cut the amount of time needed to
find a solution by well over half, reducing a
problem that might have taken years to solve
to mere hours.
 In quantum systems, the computational
space increases exponentially with the size
of the system, which enables exponential
parallelism.
 The exploitation of the properties such as
entanglement and superposition permit
some types of computations to be
performed more efficiently than the best
competing classical algorithms.

19. Limitations :
 One of the major problems of quantum
computers is that the interaction between
qubits cannot be turned on and off when
desired.
 While a quantum system can perform
massive parallel computation, access to the
results of the computation is restricted.
Accessing the results is equivalent to
making a measurement, which disturbs the
quantum state.

20. Realizations and difficulty in
building quantum computer
The quantum computer might be the
theoretician's dream, its realization is a
nightmare
 It is very difficult to scaling the component
in quantum computer
As the number of quantum gates in a
network increases, we quickly run into some
serious practical problems
The more likely it is that quantum
information will spread outside the quantum
computer and be lost into the environment,
thus spoiling the computation

21. Application :
 Quantum computing is currently being used for
encryption, long calculations and most
importantly software validation.
 As technology reaches every aspect of living,
having error free code is indispensable and a
quantum computer is the perfect solution for
testing and validating software code as quantum
computers solve problems in a more probabilistic
manner.
 Immense amount of computing power leads to
calculate impossible mathematical calculation.
Quantum computation algorithm has great
application in the field of Mathematics.
 It has wide application in cryptography (the
method of breaking ciphers).

22. Conclusion :
 It discusses an overview of the quantum
computing world.
 It discusses the inevitability of quantum
computers, how they originated, and what
is different about them from classical
computers.
 Quantum computes are coming, and they
will require a new way of looking at
computing.

23. Reference :
 E.Rieffel,W.Polak,”An IntroductionTo
Quantum Computing for Non-Physicist”,ACM
Computing Survey,Vol. 32, No.3 (2000).
 C.H.Bennet,”Quantum Information And
Computation”, PhysicsToday,American
Institute of Physics (1995).
 M.Lanzagorta, J.Uhlmann,”Hybrid Quantum-
Classical Computing with Application to
Computer Graphics”, IEEE Computer
Graphics with Application (2003).