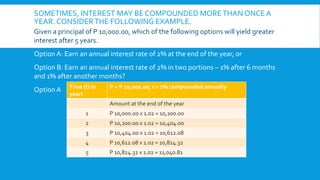
Here are the solutions: 1a) Simple Interest = Principal x Rate x Time = P 60,000 x 8% x 1 = P 60,000 x 0.08 = P 4,800 1b) Compounded annually: Interest = Principal x (1 + Rate)^Time - Principal = P 60,000 x (1 + 0.08)^1 - P 60,000 = P 60,000 x 1.08 - P 60,000 = P 4,800 1c) Compounded semi-annually: Rate per period = Annual rate / Times compounded per year = 8% / 2 = 4% Interest = Principal x (1 +

1. COMPOUNDING MORE THAN
ONCE AYEAR
ALAN S.ABERILLA

2. SOMETIMES, INTEREST MAY BE COMPOUNDED MORETHAN ONCE A
YEAR. CONSIDERTHE FOLLOWING EXAMPLE.
Given a principal of P 10,000.00, which of the following options will yield greater
interest after 5 years.
Option A: Earn an annual interest rate of 2% at the end of the year, or
Option B: Earn an annual interest rate of 2% in two portions – 1% after 6 months
and 1% after another months?
Option A Time (t) in
years
P = P 10,000.00; r = 2% compounded annually
Amount at the end of the year
1 P 10,000.00 x 1.02 = 10,200.00
2 P 10,200.00 x 1.02 = 10,404.00
3 P 10,404.00 x 1.02 = 10,612.08
4 P 10,612.08 x 1.02 = 10,824.32
5 P 10,824.32 x 1.02 = 11,040.81

3. Option B
A more frequent compounding will result in a higher interest.
T (t) in years P = P 10,000.00 ; r = 2% compounded semi-annually
Amount at the end of the year
1/2 P 10,000.00 x 1.01 = 10,100.00
1 P 10,100.00 x 1.01 = 10,201.00
1 1/2 P 10,201.00 x 1.01 = 10,303.01
2 P 10,303.01 x 1.01 = 10,406.04
2 1/2 P 10,406.04 x 1.01 = 10,510.10
3 P 10,510.10 x 1.01 = 10,615.20
3 1/2 P 10,615.20 x 1.01 = 10,721.35
4 P 10,721.35 x 1.01 = 10,828.56
4 1/2 P 10,828.56 x 1.01 = 10,936.85
5 P 10,936.85 x 1.01 = 11,046.22

4. The investment in Option B introduces new concepts because interest is
compounded twice a year, the conversion period is 6 months and the frequency of
conversion is 2. As the investment runs for 5 years, the total number of conversion
periods is 10. The nominal rate is 2% and the rate of interest for each conversion
period is 1%.
Definition ofTerms:
Frequency of conversion (m) – number of conversion period in one year
Conversion or interest period (t) – time between successive conversion of interest
Total number of conversion period (n) = n = mt
Nominal rate (i(m)) – annual of interest
Rate of interest (j) for each conversion period
j = i(m)/m = annual rate of interest/frequency of convers

5. ACTIVITY 4
COMPLETETHETABLE BELOW:
i(m) = Nominal rate
(Annual Interest
Rate)
m = frequency of
conversions
j = Interest rate
per conversion
period
One conversion
period
5% compounded
annually
3% compounded
semi-annually
4% compounded
quarterly
6% compounded
monthly
7% compounded
daily

6. Note on rate notation: r, i(m), j
In earlier lessons, r was used to describe to denote the interest rate. Now that an interest rate can
refer to two rates (either nominal or rate per conversion period), the symbols i(m) and j will be used.
MaturityValue, Compounding m times a year
F = P[(1 + i(m)/m)]mt or F = P(1 + j)mt
F = maturity (future) value
P = principal
i(m) = nominal rate of interest (annual rate)
m = frequency of conversion
t = term/time in years

7. Example 1. Find the maturity value and interest if P 10,000.00 is deposited in a bank at 2%
compounded quarterly for 5 years?
Given: P = P 10,000.00 i(4) = 0.02 t = 5 years m = 4
Find: a) F b) Ic
Solution:
a) F = P(1+j)n ; j = i(4)/ m = 0.02/4 = 0.005 ; n = mt = (4)(5) = 20
F = P 10,000.00(1 + 0.005)20
F = P 11,048.96
b. I c = F – P
I c = P 11,048.96 – P 10,000.00
I c = P 1,048.96

8. Example 2. Find the maturity value and interest if P 10,000.00 is deposited in a bank at 2%
compounded monthly for 5 years?
Given: P = P 10,000.00 i(12) = 0.02 t = 5 years m = 12
Find: a) F b) Ic
Solution:
a) F = P(1+j)n ; j = i(12)/ m = 0.02/12 ; n = mt = (12)(5) = 60
F = P 10,000.00(1 + 0.02/12)60
F = P 11,050.79
b. I c = F – P
I c = P 11,050.79 – P 10,000.00
I c = P 1,050.79

9. PresentValue P at Compound Interest
P = F/[(1 + i(m)/m)]mt or P = F/(1 + j)n
F = maturity (future) value
P = principal
i(m) = nominal rate of interest (annual rate)
m = frequency of conversion
t = term/time in years

10. Example 3. Find the present value of P 50,000.00 due in 4 years if money is
invested at 12% compounded semi-annually?
Given: F = 50,000.00 i(2) = 0.12 t = 4 m = 2
Find: F
Solution:
P = F/(1 +j)n ; j = i(2)/ m = 0.02/12 = 0.06 ; n = mt = (2)(4) = 8
F = P 50,000.00/(1 + 0.06)8
F = P 31,370.62

11. ACTIVITY 5
Solve the following: Solution:
1. Alexandra wants to compare the simple interest to compound interest
on a P 60,000.00 investment.
a) Find the simple interest if funds earn 8% simple interest for 1 year
b) Find the interest if funds earn 8% compounded annually for 1 year
c) Find the interest if funds earn 8% compounded semi-annually for 1 year
d) Find the interest if funds earn 8% compounded quarterly for 1 year

12. 2. Rafael aims to accumulate 1 Million Pesos in 12 years.Which investment
will require the smallest present value?
a) 8% simple interest
b) 8% compounded annually
c) 8% compounded semi-annually
d) 8% compounded quarterly
e) 8% compounded monthly