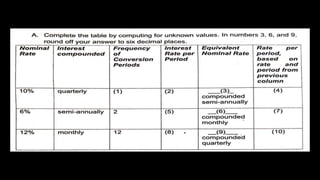
This document defines terms related to simple and compound interest such as principal, interest rate, time period, and discusses how to calculate simple interest, compound interest, maturity value, and present value. It provides examples of calculating simple interest, compound interest annually and for periods of less than 1 year. It also discusses how to find equivalent interest rates, effective rates, and the number of compounding periods or time required to reach a given future value.

1. I L L U S T R A T I N G
S I M P L E A N D
C O M P O U N D
I N T E R E S T
SIMPLE AND COMPOUND
INTEREST

2. D E F I N I T I O N O F T E R M S
Lender or creditor – person (or institution) who invests the money or
makes the funds available.
Borrower or debtor - person (or institution) who owes the money or avails
of the funds from the lender.
Origin or load date – date on which money is received by the borrower.
Repayment or maturity date – date on which the money is borrowed or
loan is to be completely repaid.

3. D E F I N I T I O N O F T E R M S
Rate (r) – annual rate, usually in percent, charged by the lender, or
rate of increase of the investment.
Time or term (t) – amount of time in years the money is borrowed or
invested; length of time between the origin and maturity dates.
Principal (P) – amount of money borrowed or invested on the origin
date.

4. D E F I N I T I O N O F T E R M S
Interest (i) - amount paid or earned for the use of money.
Simple Interest (Is) – interest that is computed on the principal and
then added to it.
Compound Interest (Ic) – interest that is computed on the principal and
also on the accumulated past interest.
Maturity value or Future value (F) – amount after t years that the lender
receives from the borrower on the maturity date.

5. S I M P L E A N D C O M P O U N D I N T E R E S T
• 1. SUPPOSE YOU WON P10,000 AND YOU
PLAN TO INVEST IT FOR 5 YEARS. A
COOPERATIVE GROUP OFFERS 2% SIMPLE
INTEREST RATE PER YEAR. A BANK OFFERS
2% COMPOUNDED ANNUALLY. WHICH
OFFER WILL YOU CHOOSE AND WHY?

6. S I M P L E A N D C O M P O U N D I N T E R E S T
• IN SIMPLE INTEREST, INTEREST REMAINS
CONSTANT THROUGHOUT THE
INVESTMENT TERM.
• IN COMPOUND INTEREST, THE INTEREST
FROM THE PREVIOUS TERMS ALSO EARNS
INTEREST. THUS, THE INTEREST GROWS
EVERY YEAR.

7. SIMPLE INTEREST

8. S I M P L E
I N T E R E S T
ANNUAL SIMPLE INTEREST
Is = Prt
where;
Is = simple interest
P = principal amount
r = simple interest rate
t = term or time in years

9. E X A M P L E 1
A bank offers 0.25% annual simple
interest rate for a particular deposit.
How much interest will be earned if 1
million pesos is deposited in this
savings account for 3 years?

10. E X A M P L E 2
How much interest is charged when
P50,000 is borrowed for 9 months at an
annual interest rate of 10%?

11. E X A M P L E 3
• Complete the table below by finding the
unknown.

12. E X A M P L E 4
When invested at an annual interest
rate of 7%, the amount earned P11,200
of simple interest in two years. How
much money was originally invested?

13. E X A M P L E 5
If an entrepreneur applies for a loan
amounting to P500,000 in a bank, the
simple interest of which is P157,500 for
3 years, what interest rate is being
charged?

14. M AT U R I T Y O R F U T U R E
VA L U E

15. M AT U R I T Y O R F U T U R E
VA L U E
F = P + Is
Where;
F = maturity (future) value
P = Principal
Is = simple interest

16. M AT U R I T Y O R F U T U R E
VA L U E
F = P (1+rt)
Where;
r = interest rate
t = term or time in years

17. E X A M P L E 6
Find the maturity if 1 million pesos is
deposited in a bank at an annual simple
interest rate of 0.25% after (a) 1 year
(b) 5 years (c) 8 years (d) 15 years?

18. E X A M P L E 7
Find the maturity value when P50,000 is
borrowed for 9 months at an annual
interest rate of 10%?

19. SEATWOR
K
#1
November 08, 2022

20. S E AT W O R K
1. What are the amounts of interest and maturity value of a loan
for P25,000 at 12% simple interest for 5 years?
2. How much money will you have after 4 years and 3 months if
you deposited P10,000 in a bank that pays 0.5% simple interest?
3. At what simple interest rate per annum will P1 become P2 in 2
years?
4. How long will 1 million pesos earn a simple interest of 100,000 at
1% per annum?
5. How much should you invest if the simple interest is 7.5% in
order to have P300,000 in 2 years?

21. COMPOUND
INTEREST
• MATURITY VALUE
• PRESENT VALUE
• COMPOUNDING MORE THAN ONCE A YEAR

22. MATURITY VALUE
𝐹 = 𝑃 1 + 𝑟 𝑡
Where
P = principal value
F = Future/ maturity value
r = interest rate
t = term/ time in years

23. COMPOUND INTEREST
the compound interest Ic is given by
𝐼𝑐 = 𝐹 − 𝑃

24. E X A M P L E 1 : C O M P O U N D I N T E R E S T
Find the maturity value and the
compound interest if P10,000 is
compounded annually at an interest
rate of 2% in 5 years.

25. E X A M P L E 2 : C O M P O U N D I N T E R E S T
Find the maturity value and the
compound interest if P50,000 is
invested at 5% compounded annually
for 8 years.

26. COMPOUND INTEREST :
PRESENT VALUE
𝑃 =
𝐹
1 + 𝑟 𝑡
Where
P = principal value
F = Future/ maturity value
r = interest rate
t = term/ time in years

27. E X A M P L E 3 : C O M P O U N D I N T E R E S T
What is the present value of P50,000
due in 7 years if money is worth 10%
compounded annually?

28. E X A M P L E 4 : C O M P O U N D I N T E R E S T
How much money should a student
place in a time deposit bank that pays
1.1% compounded annually so that he
will have P200,000 after 6 years?

29. E X A M P L E 5 : C O M P O U N D I N T E R E S T
How much money should a student
place in a time deposit bank that pays
1.1% compounded annually so that he
will have P200,000 after 6 years?

30. DEFINITION OF TERMS
FREQUENCY OF CONVERSION (m) – number of
conversion period in a year
CONVERSION OR INTEREST PERIOD – time between
successive conversions of interest

31. DEFINITION OF TERMS
NOMINAL RATE (𝑖𝑚
) - annual rate of interest
RATE (j) OF INTEREST FOR EACH CONVERSION PERIOD
𝑗 =
𝑖𝑚
𝑚
=
𝑎𝑛𝑛𝑢𝑎𝑙 𝑟𝑎𝑡𝑒 𝑜𝑓 𝑖𝑛𝑡𝑒𝑟𝑒𝑠𝑡
𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑐𝑜𝑛𝑣𝑒𝑟𝑠𝑖𝑜𝑛

33. MATURITY VALUE, COMPOUNDING
m TIMES A YEAR
𝐹 = 𝑃 1 +
𝑖𝑚
𝑚
𝑚𝑡
Where
P = principal value
F = Future/ maturity value
m = frequency of conversion
t = term/ time in years
𝑖𝑚= nominal rate of interest (annual rate)

34. E X A M P L E 1 : C O M P O U N D I N G M O R E T H A N A
Y E A R
Find the maturity value and interest if
P10,000 is deposited in a bank at 2%
compounded quarterly for 5 years.

35. E X A M P L E 2 : C O M P O U N D I N G M O R E T H A N A
Y E A R
Find the maturity value and interest if
P10,000 is deposited in a bank at 2%
compounded monthly for 5 years.

36. E X A M P L E 3 : C O M P O U N D I N G M O R E T H A N A
Y E A R
Kyle borrows P50,000 from Henny and
promises to pay the principal and
interest at 12% compounded monthly.
How much must he repay after 6 years?

37. COMPOUND INTEREST :
PRESENT VALUE
𝑃 =
𝐹
1 +
𝑖𝑚
𝑚
𝑚𝑡
Where
P = principal value
F = Future/ maturity value
m = frequency of conversion
t = term/ time in years
𝑖𝑚
= nominal rate of interest (annual rate)

38. E X A M P L E 4 : C O M P O U N D I N G M O R E T H A N A
Y E A R
Find the present value of P50,000 due in 4 years
if money is invested at 12% compounded semi-
annually.

39. E X A M P L E 5 : C O M P O U N D I N G M O R E T H A N A
Y E A R
What is the present value of P25,000 due in 2
years and 6 months if money is worth 10%
compounded quarterly?

40. SEATWOR
K
#2
November 11, 2022

42. B
C
(BONUS)
(13)

43. COMPOUND
INTEREST
• FINDING INTEREST RATE AND TIME

44. DEFINITION OF TERMS
NOMINAL RATE (𝑖𝑚
) - annual rate of interest
RATE (j) OF INTEREST FOR EACH CONVERSION PERIOD
𝑗 =
𝑖𝑚
𝑚
=
𝑎𝑛𝑛𝑢𝑎𝑙 𝑟𝑎𝑡𝑒 𝑜𝑓 𝑖𝑛𝑡𝑒𝑟𝑒𝑠𝑡
𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑐𝑜𝑛𝑣𝑒𝑟𝑠𝑖𝑜𝑛

45. DEFINITION OF TERMS
EQUIVALENT RATES - two annual rates with different
conversion periods that will earn the same maturity
value for the same time/term.
EFFECTIVE RATE – rate when compounded annually will
give the same compound each year with the nominal
rate; denoted by − 𝑖1

46. MATURITY VALUE, COMPOUNDING
m TIMES A YEAR
𝐹 = 𝑃 1 +
𝑖𝑚
𝑚
𝑚𝑡
Where
P = principal value
F = Future/ maturity value
m = frequency of conversion
t = term/ time in years
𝑖𝑚= nominal rate of interest (annual rate)

47. FINDING THE NUMBER OF PERIODS
n
𝐹 = 𝑃 1 + 𝑗 𝑛
Then,
𝑙𝑜𝑔𝐹 = 𝑙𝑜𝑔 1 + 𝑗 𝑛
= 𝑛𝑙𝑜𝑔(1 + 𝑗)
Thus,
𝑛 =
𝑙𝑜𝑔𝐹
𝑚𝑙𝑜𝑔 1 + 𝑗
Note that n, must be an integer. Some rounding off may be

48. E X A M P L E 1 : F I N D I N G I N T E R E S T R AT E S A N D
T I M E
How long will it take P3,000 to
accumulate P3,500 in a bank savings
account at 0.25% compounded
monthly?

49. E X A M P L E 2 : F I N D I N G I N T E R E S T R AT E S A N D
T I M E
How long will it take P1,000 to earn
P300 if the interest is 12% compounded
semi-annually?

50. FINDING THE INTEREST RATE j,
PER CONVERSION PERIOD
𝐹 = 𝑃 1 + 𝑗 𝑛
Then,
𝑛 𝐹
𝑃
= 1 + 𝑗
Thus,
𝑗 =
𝑛 𝐹
𝑃
− 1 using 𝑗 =
𝑖
𝑚
, then 𝑖 = 𝑗𝑚

51. E X A M P L E 3 : F I N D I N G I N T E R E S T R AT E S A N D
T I M E
At what nominal rate compounded
semi- annually will P10,000 accumulate
to P15,000 in 10 years?

52. E X A M P L E 4 : F I N D I N G I N T E R E S T R AT E S A N D
T I M E
At what interest rate compounded
quarterly will money be double itself in
10 years?

53. E X A M P L E 5 : F I N D I N G I N T E R E S T R AT E S A N D
T I M E
What effective rate is equivalent to 10%
compounded quarterly?

54. E X A M P L E 6 : F I N D I N G I N T E R E S T R AT E S A N D
T I M E
What nominal rate compounded
monthly is equivalent to 12%
compounded annually? Round off to six
decimal places.

55. F I N D I N G T H E E F F E C T I V E A N D
E Q U I VA L E N T R AT E S
For Equivalent rates F1=F2, then
𝑃 1 +
𝑖1
𝑚1
𝑚1
𝑡
= 𝑃 1 +
𝑖2
𝑚2
𝑚2
𝑡
Dividing both sides by P and getting the t root will give us,
1 +
𝑖1
𝑚1
𝑚1
= 1 +
𝑖2
𝑚2
𝑚2
For different compounding modes m1 & m2

56. F I N D I N G T H E E F F E C T I V E A N D
E Q U I VA L E N T R AT E S
𝐸𝑅𝐼 = 1 +
𝑖
𝑚
𝑚
− 1
For effective rate, the mode is for an annual compounding.
It is the actual interest earned in one-year period.

57. E X A M P L E 7 : F I N D I N G E F F E C T I V E A N D
E Q U I VA L E N T R AT E S
What is the effective rate corresponding
to 18% compounded daily? Take 1 year
equal to 360 days.

58. E X A M P L E 8 : F I N D I N G E F F E C T I V E A N D
E Q U I VA L E N T R AT E S
What nominal rate compounded
monthly is equivalent to 12%
compounded annually? (6 decimal
places)

59. E X A M P L E 9 : F I N D I N G E F F E C T I V E A N D
E Q U I VA L E N T R AT E S
What nominal rate, compounded semi-
annually, yields the same amount as
25% compounded quarterly?

60. E X A M P L E 1 0 : F I N D I N G E F F E C T I V E A N D
E Q U I VA L E N T R AT E S
What rate of interest compounded
annually is the same as the rate of
interest of 8% compounded quarterly?

61. E X A M P L E 1 1 : F I N D I N G I N T E R E S T R AT E S
A N D T I M E
Complete the table by computing for the rates equivalent to
the following nominal rates. Round off to six decimal places.

62. SEATWOR
K
#3
November 22, 2022